Revista Electrónica Educare (Educare Electronic Journal) EISSN: 1409-4258 Vol. 26(3) SETIEMBRE-DICIEMBRE, 2022: 1-24
doi: https://doi.org/10.15359/ree.26-3.1
https://www.revistas.una.ac.cr/index.php/educare
educare@una.ac.cr
[Cierre de edición el 01 de Setiembre del 2022]
Criterios de evaluación referidos, percibidos y utilizados por el profesorado de matemáticas de la educación primaria
Assessment Criteria Cited, Perceived, and Used by Mathematics Teachers in Primary Education
Critérios de avaliação referidos, percebidos e utilizados pela equipe docente de matemática de ensino básico
Maria-João Marques-Oliveira
Agrupamento de Escolas da Lourinhã
Lourinhã, Portugal
mariajoaop@sapo.pt
 https://orcid.org/0000-0002-8482-9662
https://orcid.org/0000-0002-8482-9662
Manuel Montanero
Universidad de Extremadura
Badajoz, España
mmontane@unex.es
 https://orcid.org/0000-0002-2153-1180
https://orcid.org/0000-0002-2153-1180
Recibido • Received • Recebido: 11 / 05 / 2020
Corregido • Revised • Revisado: 15 / 05 / 2022
Aceptado • Accepted • Aprovado: 21 / 06 / 2022
Resumen:
Objetivo. El principal propósito de este trabajo es comparar los criterios de evaluación que el profesorado de la educación primaria considera más relevantes en el área de matemáticas, con la percepción que tiene su propio estudiantado, así como con la observación de los criterios que realmente utiliza en la práctica. Metodología. Para ello, entrevistamos a 30 maestros y maestras y 120 estudiantes. Además, el profesorado participó en una actividad de evaluación ciega, basada en el método de descubrimiento de criterios, que consistía en calificar una prueba con varias tareas matemáticas, que había sido previamente resuelta por un alumno o alumna, haciendo preguntas a la entrevistadora, pero sin poder ver el documento. Resultados. A partir de las trascripciones de las respuestas registradas durante las entrevistas, se realizó un análisis de contenido, para categorizar y comparar los criterios de evaluación referidos (por el personal docente), percibidos (por el alumnado) y los realmente utilizados (en la evaluación ciega). Discusión y conclusiones. Los resultados sugieren que, en general, el profesorado considera el cálculo mental, la comprensión y, sobre todo, el razonamiento matemático como los criterios más importantes. Sin embargo, la mayoría de su alumnado no tiene la misma percepción. Además, un tercio aproximadamente de los maestros y las maestras no manifiestan una conciencia suficientemente precisa de los criterios que realmente aplican en las pruebas de evaluación. Finalmente, se discuten algunas implicaciones para la mejora de las prácticas de evaluación de esta área curricular.
Palabras-claves: Evaluación educativa; Pensamiento del profesorado; Criterios de evaluación; Evaluación ciega; Matemáticas; Educación Primaria.
Abstract:
Objective. This work mainly aims to compare the assessment criteria considered most relevant by Mathematics teachers in Elementary Education with those they actually use and the perception their students have. Method. To this effect, we interviewed 30 teachers and 120 students. Additionally, the teachers participated in a blinded assessment of one student’s exam based on the criteria discovery method. They were asked to grade a test involving several mathematical tasks which a student had previously solved. They could ask questions to the interviewer without seeing the document. Results. Based on the transcriptions of the interviews, a content analysis was conducted to categorize and compare the assessment criteria expressed (by the teachers), perceived (by the students), and those used (in the blind assessment). Discussion and conclusions. The results suggest that teachers consider mental arithmetic, comprehension, and, above all, mathematical reasoning as the most important criteria. However, most of their students do not have the same perception. Furthermore, a third of the teachers are not sufficiently aware of the assessment criteria they are, in fact, using. Finally, we discuss the influence of assessment in mathematics.
Keywords: Educational assessment; teachers’ thinking; assessment criteria; blinded assessment; mathematics; elementary education.
Resumo:
Objetivo. O principal objetivo deste trabalho é comparar os critérios de avaliação que os docentes docente do Ensino Básico mais valorizam na disciplina de Matemática, com os que efetivamente utilizam na prática, e com a perceção que têm os seus próprios alunos. Metodologia. Para isso, entrevistamos 30 docentes e 120 estudantes. Os docentes participaram, ainda, numa atividade de avaliação cega de uma prova realizada por um dos seus alunos, baseada no método de descoberta de critérios, que consistia em classificar a prova com várias tarefas matemáticas, fazendo perguntas à investigadora, mas sem poder ver o documento. Resultados. A partir das transcrições das respostas registadas durante as entrevistas, realizou-se uma análise de conteúdo, para categorizar e comparar os critérios de avaliação referidos (na entrevista ao grupo docente), percecionados (na entrevista aos alunos) e os efetivamente utilizados (na avaliação cega). Discussão e conclusões. Os resultados sugerem que os docentes consideram, entre os critérios mais importantes, avaliar a compreensão e, sobretudo, o raciocínio matemático. Porém, a maioria dos seus alunos não têm a mesma perceção. Além do mais, um terço aproximadamente dos docentes não mostrou uma consciência suficientemente precisa dos critérios de avaliação que realmente aplica nas provas de avaliação. Finalmente, discutem-se algumas implicações para a melhoria das práticas de avaliação desta área curricular.
Palavras-chave: Avaliação educacional; pensamento da equipe docente; critérios de avaliação; avaliação cega; matemática; ensino básico.
Introducción
La evaluación escolar es una de las cuestiones más controverstidas y que suscita más interés en los diferentes agentes educativos, desde la administración, hasta el profesorado y las familias, pasando por el propio alumnado. En el área de matemáticas, en particular, la constatación del bajo rendimiento de un elevado número de estudiantes en la educación obligatoria hace necesario un mayor esfuerzo de investigación sobre el pensamiento del profesorado y las prácticas de evaluación en el aula. En este marco, la presente investigación pretender aportar información sobre los criterios que el personal docente de educación primaria tiene realmente en cuenta a la hora de evaluar las pruebas que realizan los niños y niñas en esta etapa educativa, cómo los aplican a la hora de calificar dichas pruebas, y qué grado de consciencia de estos, tanto en el alumnado, como en el propio profesorado.
Entendemos por evaluación educativa el proceso de recogida de información que conduce a un juicio de valor sobre algún aspecto de la enseñanza o el aprendizaje del alumando (Montanero, 2019), y como un punto de partida para tomar decisiones (Coll et al., 2000; Melo y Veiga, 2013). Dicho juicio se basa, explícita o implícitamente, en determinados criterios que el profesorado considera como referencia para interpretar aquella información. En este sentido, los criterios de evaluación constituyen los estándares e indicadores observables del grado de aprendizaje que alcanza el alumnado. Además de su dimensión normativa, que toma como referencia el currículo oficial para cada nivel educativo, los criterios de evaluación deben tener un enfoque personalizado, centrado en las características, necesidades y progreso del propio sujeto que se evalúa (de Ory Azcárate y Ruiz Suárez, 2011).
Los criterios de evaluación pueden tener un sentido formativo, cuando el personal docente centra su evaluación en regular el proceso de enseñanza y adecuar su ayuda a las necesidades del alumnado (Black y Wiliam, 1998). En un sentido sumativo y social, se orienta también a acreditar las competencias y aprendizajes finalmente adquiridos, necesarios para participar con aprovechamiento en futuros procesos de formación (Onrubia y Lago, 2008).
En el caso particular de las matemáticas, algunos estudios han mostrado la dificultad de establecer un sistema de criterios, suficientemente simple y completo, que permita evaluar la competencia matemática (Teledahl, 2015). A pesar de ello, se han publicado diversas propuestas, entre las que cabe destacar los Principios y criterios para la educación matemática (National Council of Teachers of Mathematics [NCTM], 2000) y el Marco de alfabetización matemática (Organization for Economic Cooperation and Development [OECD], 2013). De acuerdo con el trabajo del grupo experto de PISA, en esta área curricular los criterios de evaluación deberían fundamentarse concretamente en 6 elementos competenciales: (1) la comprensión y comunicación de enunciados con información matemática; (2) la comprensión y utilización de símbolos, formalismos propias del lenguaje matemático; (3) la matematización o traslación a modelos matemáticos de situaciones problemáticas; (4) la decodificación y utilización de representaciones matemáticas; (5) la selección y utilización de estrategias para resolver problemas matemáticos; (6) el razonamiento y la argumentación matemática (Turner et al., 2015).
En el ámbito específico de la solución del problema matemáticos, dichos criterios deberían contemplar procedimientos y habilidades cognitivas, implicadas en (a) comprender el enunciado del problema y construir una representación situacional, en la que selecciona la información relevante; (b) razonar sobre dicha representación, para contruir y contrastar un modelo matemático, en función del cual planificar las operaciones matemáticas necesarias para la solución del problema; (c) realizar los algoritmos implicados en esas operaciones; (d) intepretar el resultado y, en su caso, revisarlo y comunicarlo (Kintsch y Greeno, 1985; Selter et al., 2000).
El progresivo consenso acerca de este tipo de propuestas no supone, sin embargo, que el profesorado las asuma realmente en la práctica del aula. La toma de conciencia y concreción de los criterios de evaluación es un requisito esencial de la calidad de la evaluación (Black y Wilian, 2009; Pinto y Santos, 2006) que tiene una influencia directa en los procesos y resultados de aprendizaje (Barbosa y Alaíz, 1994; Pacheco, 2002; Struyven et al., 2005). No cabe duda de que la precisión con que el estudiantado interpreta las demandas del profesorado condiciona sus producciones en el aula (Hadji, 2001). Sin embargo, algunos estudios han encontrado evidencias de una fuerte discrepancia entre los criterios de evaluación que el profesorado declara tener en cuenta y los que realmente utilizan, así como los que sus estudiantes perciben (Nunes, 1990).
En este sentido, se echan en falta trabajos que estudien el pensamiento y la práctica real del profesorado de matemáticas acerca de la evaluación, así como la percepción que tiene el propio alumnado sobre lo que sus docentes valoran realmente en las actividades de evaluación. Se trata de una cuestión muy relevante, pero de difícil investigación, dada la dificultad de acceder al estudio de los criterios de evaluación que el personal docente utiliza en su práctica educativa.
El procedimiento más extendido para obtener información sobre las prácticas evaluativas del profesorado de matermáticas se ha basado en entrevistas o cuestionarios (Riggan y Nabors Oláh, 2011; Suurtamm et al., 2010; Veldhuis et al., 2013). Los métodos de autoinforme están, no obstante, fuertemente amenazados por el riesgo de que el profesorado no tenga una conciencia suficientemente precisa de los criterios implícitos que guían realmente algunas de sus decisiones en la práctica del aula.
Una alternativa metodológica mucho menos frecuente consiste en la observación de las decisiones que el profesorado toma en situaciones reales de evaluación. Onrubia y Lago (2008), por ejemplo, pidieron a docentes de matemáticas que verbalizaran las valoraciones y decisiones que tomaban durante la evaluación de una tarea. Las técnicas de pensamiento en voz alta requieren, empero, un considerable entrenamiento para conseguir que los sujetos informantes automaticen la producción de verbalizaciones y que estas traduzcan con cierta fiabilidad las impresiones que les vienen a la mente durante la actividad de evaluación.
Otra técnica observacional, que no ha sido utilizada en matemáticas, consiste en la evaluación ciega de una prueba con una o más tareas curriculares, previamente resueltas por un alumno o una alumna (Noizet y Caverni, 1985). A diferencia del pensamiento en voz alta, al profesorado no se le permite ver las respuestas del estudiantado, pero sí formular, a quien entrevista, todas las cuestiones que considerasen necesarias y se les pide que justifiquen sus calificaciones. De este modo, es posible forzar la explicitación del pensamiento del profesorado acerca de lo que considera más importante en la tarea, de modo que podamos posteriormente inferir los criterios que tiene en cuenta para evaluarla y calificarla.
Nuestra investigación se fundamentó en esta última estrategia para contrastar el pensamiento y la práctica del profesorado en la evaluación de tareas matemática de la educación primaria. En concreto, nos planteamos dos objetivos específicos de investigación:
1. Documentar la diversidad de criterios que el profesorado de los primeros cursos de la educación primaria refiere explícitamente como más relevantes para evaluar pruebas o exámenes de matemáticas, así como la percepción que manifiesta su alumnado de dichos criterios.
2. Analizar el grado de concordancia entre los criterios referidos como más relevantes por el profesorado de matemáticas, los que su alumnado considera más importantes, y los criterios que dicho profesorado realmente aplica en una prueba de evaluación convencional.
Método
La investigación se planteó desde un enfoque mixto, cualitativo y cuantitativo, basado en el análisis del contenido verbal de las entrevistas a los participantes.
Participantes
El estudio fue realizado en 14 escuelas de Enseñanza Básica del distrito de Lisboa (Portugal). Se seleccionaron por conveniencia 26 maestras y 4 maestros, con edades comprendidas entre los 27 y los 50 años y una experiencia docente relativamente amplia (entre los 5 y los 22 años). La mitad enseñaban en segundo curso (13 mujeres y 2 hombres), y la otra mitad en cuarto (también 13 mujeres y 2 hombres).
De cada uno de los 30 grupos de niños y de niñas en los que el profesorado seleccionado impartía docencia se selecionaron también 4 estudiantes: 2 con rendimiento académico normal y 2 con rendimiento bajo (no satisfactorio) en matemáticas, de acuerdo con la primera evaluación del curso. La muestra de alumnado estuvo, por tanto, compuesta por un total de 60 niños y 60 niñas. Ninguno de ellos ni ninguna de ellas había repetido curso escolar. La media de edad era de 7,2 en 2º curso y 10,3 años en 4º. Provenían de un entorno social y familiar de nivel socioeconómico similar (medio-bajo).
Instrumentos y materiales
Entrevistas semiestructuradas
Para el proceso de recogida de datos fueron construidas dos entrevistas semiestructuradas, una direccionada al personal docente y otra al estudiantado. La entrevista al profesorado tenía como objetivo identificar los criterios que consideran más relevantes para la evaluación de la competencia matemática, a partir de las siguientes cuestiones: ¿a qué le da más importancia al evaluar una prueba de matemáticas?; ¿qué criterios utiliza en la evaluación de dichas pruebas?; ¿qué criterios de evaluación considera más importantes en matemáticas?
La entrevista al alumnado pretendía recoger información acerca de los criterios de evaluación que perciben y los que consideran que tienen más influencia en sus calificaciones. Fueron formuladas las siguientes cuestiones abiertas: ¿qué piensas que es preciso hacer para conseguir una buena calificación en un examen de matemáticas?; ¿qué consejos darías a un compañero o compañera para tener una buena calificación en una prueba de matemáticas?
Prueba de evaluación
A partir de la revisión de un conjunto de actividades de evaluación propuestas en libros de texto de 2º y 4º curso, se elaboraron sendas pruebas de evaluación, una para 2º y otra para 4º curso. Las pruebas incluían ejercicios de lectura y escritura de números, cálculo aritmético y solución de problemas. Fueron pre-testadas en dos grupos de 2º y 4º año (con alumnado que no participó en el estudio); fruto de lo cual se efectuaron ligeras modificaciones para equilibrar su dificultad.
Procedimiento de recogida de datos
Entrevista al profesorado (criterios referidos)
La entrevista individual con el personal docente se centró en conocer los criterios de evaluación referidos como más importantes en la evaluación, de acuerdo con las preguntas que enunciábamos anteriormente. Las respuestas fueron grabadas y transcritas. Veamos un ejemplo de las respuestas de uno de los maestros a dichas preguntas:
Entrevistadora: ¿Qué valora más en la evaluación de una prueba de matemáticas?
Profesora 1: A lo que más valor le doy es a la solución de problemas.
Entrevistadora: ¿Qué criterios utiliza en la evaluación de una prueba de matemáticas?
Profesora 1: Pues … considero el razonamiento, la resolución de operaciones, si están bien escritos los números (las centenas, decenas, unidades …)
Entrevistadora: Pero de todos ellos, cuál es el criterio de evaluación que considera más importante
Profesora 1: El razonamiento.
Entrevista al alumnado (criterios percibidos)
En la entrevista individual a la muestra del alumnado, la entrevistadora, después de un breve período de familiarización, planteaba preguntas similares sobre la percepción de los criterios más importantes en la evaluación en matemáticas, como en el siguiente fragmento con un estudiante de 4º con rendimiento medio-alto:
Entrevistadora: ¿Qué piensas que es necesario hacer para tener una buena nota en un examen de matemáticas?
Alumno 2: Tienes que mirar con mucha atención los ejercicios, las frases que están escrita encima para saber qué es lo que tenemos que hacer en ese ejercicio; si no, lo tienes luego todo mal.
Entrevistadora: ¿Qué consejos darías a otro niño o niña para conseguir una buena nota en una prueba de matemáticas?
Alumno 2: Prestar mucha atención a las cuentas, intentar no tener fallos, hacer bien los números, hacer los ejercicios con cuidado, mirar bien lo que hay escrito…
Las respuestas fueron también grabadas e íntegramente transcritas para su posterior análisis.
Evaluación ciega de una prueba de matemáticas (criterios utilizados)
Para poder observar en la práctica los criterios de evaluación de tareas matemáticas que realmente utilizaba el personal docente, diseñamos una actividad de evaluación ciega, basada en el método de descubrimiento de criterios, propuesto originalmente por Noizet y Caverni (1985), y que ha sido utilizada en actividades de evaluación de la lectoescritura (véase Alves Martins et al., 1991; Nunes, 1990).
La entrevistadora se desplazó de nuevo al centro escolar para solicitar, a cada profesor y profesora que había entrevistado, que participase en un juego que consistía en calificar una prueba con varias tareas matemáticas, que había sido resuelta por una niña o un niño, sin poder verla. El personal docente podía formular a la entrevistadora todas las cuestiones que considerase necesarias (tanto sobre los enunciados de las tareas como sobre las respuestas registradas por el estudianteo la estudiante), sin límite de tiempo, pero sin poder acceder a la visualización directa de la prueba hasta el final. La entrevistadora respondía de forma concreta y escueta cuando la pregunta era clara. En cambio, solicitaba una reformulación de la pregunta cuando esta era ambigua o imprecisa. Finalizadas las preguntas, el profesorado calificaba la ficha y, solo después, se le permitía verla. Finalmente, se le preguntaba: (a) si mantenía la calificación otorgada antes de verla y (b) qué criterios había tenido en cuenta para dicha calificación final. Toda la interacción verbal fue grabada y transcrita, como en el siguiente ejemplo, uno de los más breves, correspondiente al profesor 29 de 4º curso:
Profesora: ¿Hay problemas en los que haya que escribir números decimales o no?
Entrevistadora: Sí hay.
Profesora: ¿Las operaciones están incluidas en las situaciones problemáticas?
Entrevistadora: Sí, pero también fuera de ellas
Profesora: ¿Cómo las ha resuelto? ¿Están todas correctas?
Entrevistadora: Hay dos partes: una está correcta y la otra no.
Profesora: ¿Cuántas cuestiones tiene la primera parte?
Entrevistadora: 6 cuestiones
Profesora: ¿Y problemas?
Entrevistadora: 3.
Profesora: ¿Las operaciones son con número decimales o no?
Entrevistadora: Hay una multiplicación con números decimales y una división con números enteros.
Profesora: ¿Las ha hecho bien?
Entrevistadora: Una está bien y la otra no.
Profesora: ¿Y las ٥ cuestiones cómo están?
Entrevistadora: La escritura de números está bien.
Profesora: ¿Y los problemas están todos correctos?
Entrevistadora: Sí, bueno, dos de ellos. En el tercero el resultado no está correcto.
Profesora: No necesito saber más. Le pondría un Muy bien.
Entrevistadora: Entonces ahora vas a ver la prueba. Después me dices si mantienes la calificación o la cambias y por qué. [El profesor dedica un par de minutos a leer la hoja de la prueba]
Profesora: Le pondría un Bien, pero no Muy bien, porque debía haber hecho mejor las cuentas, hacer una lectura de dos números correcta y saber que este número decimal era mayor.
Procedimiento de análisis de datos
Análisis del contenido de las trascripciones de las entrevistas
A partir de las trascripciones de las respuestas registradas durante las entrevistas, así como durante la actividad de evaluación ciega, se realizó un análisis de contenido, para categorizar los criterios referidos (entrevista al personal docente), percibidos (entrevista al alumnado) y utilizados (evaluación ciega).
En primer lugar, las trascripciones de las respuestas fueron segmentadas semánticamente en ideas. En segundo lugar, se seleccionaron las ideas que hacían directamente referencia a criterios de evaluación, es decir, a indicadores o estándares implícitos que se tomaron como referencia para evaluar o calificar la solución de problemas matemáticos. En tercer lugar, se categorizaron dichas ideas. El sistema de categorías emergente se confeccionó y revisó en un proceso inductivo-deductivo de comparación permanente. Tras un primer ciclo de categorización, se examinaron las relaciones de semejanza entre algunas categorías, con objeto de modificar su definición, reagruparlas, diversificarlas y jerarquizarlas, hasta que se alcanzó una clasificación exhaustiva de categorías mutuamente excluyentes. Finalmente se estimó la fiabilidad de la categorización, calculando el grado de concordancia entre dos codificadores (división del número de acuerdos entre codificadores por el total de categorizaciones efectuadas). Se obtuvo un 81% de acuerdos, resolviéndose las discrepancias por consenso.
Medidas
Para cuantificar la importancia concedida a cada uno de los criterios de evaluación (referidos por el personal docente o percibidos por el alumnado) se calculó la proporción de profesorado y alumnado que los mencionaron al menos una vez, es decir, el porcentaje de entrevistas en las que encontramos al menos un registro verbal de una idea clasificada en una categoría criterial determinada.
Igualmente, para cuantificar la utilización de cada uno de los criterios utilizados durante la evaluación ciega, se calculó la proporción del profesorado que verbalizó al menos un comentario o pregunta que fuera clasificada en una de las categorías.
Para medir la discrepancia entre las categorías criteriales que encontramos en las entrevistas (criterios referidos por el personal docente o percibidos por el alumnado) y los realmente utilizados en la actividad de evaluación ciega empleamos el índice de Jaccard (Jaccard, 1901). La adaptación de esta medida al ámbito de la evaluación educativa (Alves Martins et al., 1991; Nunes, 1990) consiste en una estimación cuantitativa que mide la proximidad entre las distribuciones de los criterios referidos y utilizados por cada docente, mediante el siguiente cálculo: a/(a+b+c); donde a es igual al número de criterios referidos y utilizados por cada docente, b es el número de criterios no referidos y utilizados, y c es el número de criterios referidos y no utilizados.
En el caso del alumnado, la fórmula es la siguiente: a/(a+b), donde a representa el número de criterios utilizados por el profesorado y percibidos por el alumnado; b es el número de criterios utilizados por el profesorado y no percibidos por el alumnado.
En ambos casos, cuanto mayor es el valor resultante, cabe inferir una mayor convergencia entre los criterios referidos y los utilizados por el personal docente o percibidos por el alumnado.
Resultados
El análisis de las trascripciones de las entrevistas, así como de las verbalizaciones grabadas durante la tarea de evaluación ciega, generó un total de 21 categorías de criterios de evaluación, que posteriormente se agruparon en 6 dimensiones. La Tabla 1 recoge el sistema de categorías que emergió al final del procedimiento inductivo de análisis de contenido, junto con algunos ejemplos de registros verbales.
Tabla 1: Sistema de categorías construido a partir de los registros verbales grabados en las entrevistas al profesorado (criterios referidos), al alumnado (criterios percibidos), así como durante la actividad de evaluación ciega (criterios utilizados)
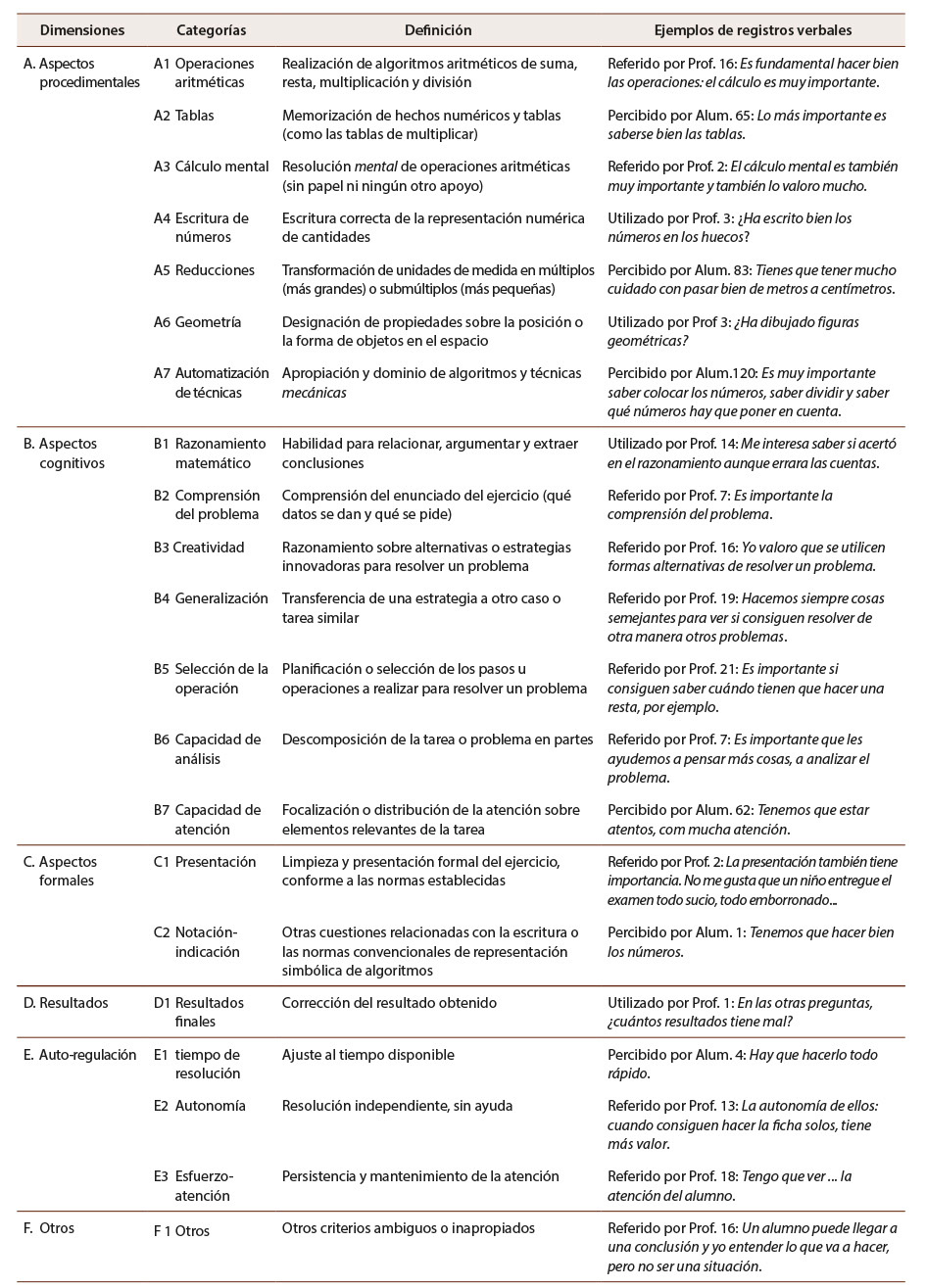
Nota: Elaboración propia.
Criterios de evaluación referidos por el profesorado en las entrevistas
El razonamiento matemático fue el único criterio de evaluación referido en las entrevistas por la casi totalidad del personal docente. Por el ejemplo, la profesora 17 declara lo siguiente: Pueden equivocarse en una cuenta, que eso para mí no tiene mucha importancia, si muestran un razonamiento correcto. Algunos maestros y algunas maestras destacan, además, el valor esencialmente formativo, más que sumativo, de este criterio, como se aprecia en el siguiente fragmento de la entrevista a esta misma profesora:
Profesora 17: Es importante entender el razonamiento del niño, por que muchas veces ellos van por un camino que no es el correcto, pero es el que ellos pensaban. Por eso hay siempre una cierta lógica en el pensamiento de los niños, que muchas veces es diferente del nuesto o que no siempre es el más correcto. Pero es fundamental enteder cuál fue esa lógica que siguieron, para poder explicarles y cambiarles algunas cosas.
La mayoría de los maestros y de las maestras aludieron también a la comprensión de los problemas y al cálculo mental como criterios relevantes. Así, el profesor 7 expresa: Es importante la comprensión. El objetivo principal de las matemáticas es siempre la resolución de situaciones problemáticas. Si el niño comprende, consigue llegar a un resultados favorable. Por su parte, el profesor 6 afirma: Para la calificación de las cuestiones tengo en cuenta el cálculo mental: pienso que el cálculo mental es la base.
Por último, la mitad del profesorado reconoce prestar mucha importancia también al resultado final de la tarea:
Profesora 5: Hago el sumatorio de las preguntas que fallan y al final pongo un Excelente, Muy bien, Bien o Insuficiente. Califico cada pregunta. Pongo Bien a un alumno que tiene todos los resultados correctos, pero no le pongo una nota superior si tuve que corregir algunos.
Una parte del profesorado matiza, sin embargo, que dicho criterio se pondera en función del razonamiento mostrado por el estudiantado, como se aprecia en el siguiente fragmento:
Profesora 21: Califico cada pregunta dependiendo del alumno. Si fuera Juan, por ejemplo, si el razonamiento es acertado, a pesar de que la cuenta esté mal, lo valoro, por que lo entendió. Pero a Bruno ya no le doy la misma facilidad si el resultado estuviera completamente equivocado o no sé de dónde viene. El valor que le daría sería muy inferior al de Juan.
En torno a una cuarta parte del profesorado menciona también otros criterios procedimentales, relacionados con la corrección y automatización de las operaciones aritméticas o la escritura de números. El resto de criterios de evaluación son referidos solo por una pequeña minoría de maestros y maestras.
Criterios de evaluación percibidos alumnado en la entrevista
Los criterios de evaluación a los que alude la mayoría del estudiantado en las entrevistas son la corrección de las operaciones aritméticas y de los resultados finales, como se aprecia en el siguiente fragmento:
Alumna 17: Tienes que hacer las cuentas todas bien y no tener ningún error para sacar todo el examen. Tenemos que tener mucho cuidado con las cuentas por que pueden ser un poquito difíciles. Algunas veces escribo las cuentas en el papel y otras veces hago las cuentas con los dedos. ... La gente tiene que sabe las cuentas y sacar los resultados siempre…, para tenerlo todo bien.
No obstante, un 41% y un 35% del alumnado señaló más o menos explícitamente cuestiones relacionadas con el razonamiento matemático o la comprensión de los problemas, respectivamente. El alumno 67, por ejemplo, alude a los riesgos de resolver mecánicamente los problemas, sin analizar antes lo que realmente se pide: Es necesario pensar, leer bien los problemas, porque a veces no son como parecen.
Bastantes estudiantes aluden también a la importancia de la concentración en la tarea (44%), la escritura correcta de números enteros y decimales (34%) y la memorización de la tabla de multiplicar (24%). El resto de criterios son mencionados por menos de una quinta parte del alumnado.
Criterios de evaluación utilizados en la actividad de evaluación ciega
El razonamiento es también el criterio más utilizado en la práctica por la totalidad del profesorado en la situación de evaluación ciega, como se aprecia en el siguiente comentario que una de las maestras verbaliza al final de la actividad de evaluación ciega: Yo le pondría más nota, por que ella ha razonado bien la operación de cálculo. Quizá se equivocó en la cuenta, por no saberse bien la tabla [de multiplicar] (Profesora 16).
No obstante, casi todo el profesorado pregunta también por la corrección del resultado final. Además, este criterio que tiene mucha influencia en la calificación que se otorga a la prueba, como se aprecia en el comentario final del profesor 19, refieriéndose a errores en los resultados numéricos de algunas tareas: Yo le pondría una nota baja; la prueba es muy sencilla; hay cosas que no se perdonan. En este mismo sentido, un 70% del profesorado solicita también información acerca de las operaciones aritméticas (Prof. 16: ¿Y las operaciones las hizo correctamente?); y un 80% pregunta explícitamente cómo están escritos los números (Prof. ١: ¿Hay ejercicios sobre escritura de números? ¿Los ha hecho bien o no?).
Otros criterios que son utilizados con cierta frecuencia tienen que ver con el cálculo mental (26%) o el conocimiento de la tabla de multiplicar (36%). El resto de criterios tiene una presencia muy minoritaria.
Comparación global entre los criterios de evaluación referidos, percibidos y utilizados
En la Tabla 2 se compara la frecuencia de ocurrencia de cada una de las anteriores categorías de registros verbales, junto con el porcentaje de sujetos que los verbalizó al menos una vez.
Tabla 2: Frecuencia y proporción del profesorado y alumando que refirió/percibió cada criterio de evaluación en las entrevistas, así como del personal docente que los utilizó en la actividad de evaluación ciega
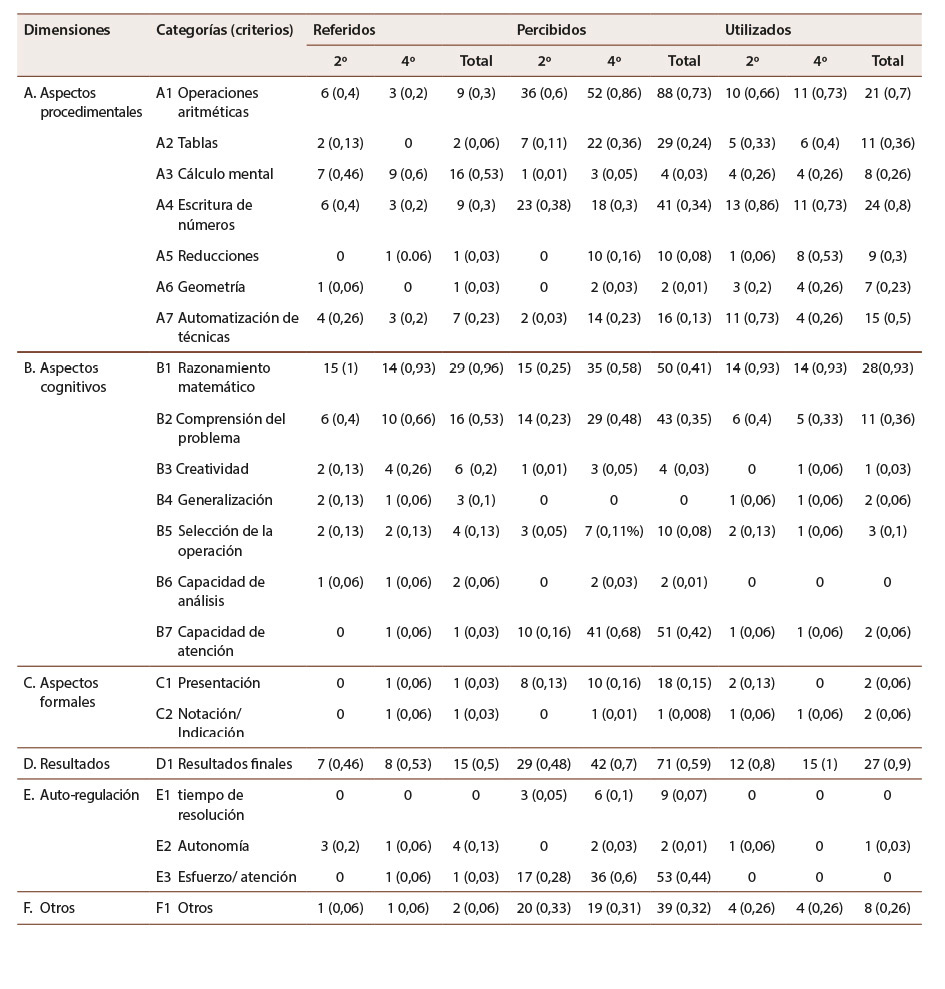
Nota: Elaboración propia.
Como puede apreciarse en el siguiente gráfico, el razonamiento matemático es el criterio más frecuentemente mencionado y utilizado. Sin embargo, se observa una clara discrepancia (de entre 40 y 50 puntos) entre el porcentaje de maestras y maestros que refiere al menos una vez en las entrevistas los criterios relativos a la corrección de las operaciones, la escritura de números o el resultado final, y el porcentaje del profesorado que los tiene en cuenta en la evaluación ciega.
El porcentaje de los estudiantes que percibe la corrección de las operaciones como uno de los criterios más relevantes, en cambio, se aproxima mucho al porcentaje de utilización en la evaluación ciega (Figura 1). No ocurre lo mismo en el resto de los criterios percibidos como importantes por una parte significativa del estudiantado, cuyos porcentajes difieren bastante de los criterios utilizados.
Figura 1: Porcentaje de profesorado que refirió y utilizó los principales criterios de evaluación, así como del alumnado que declaró percibirlos
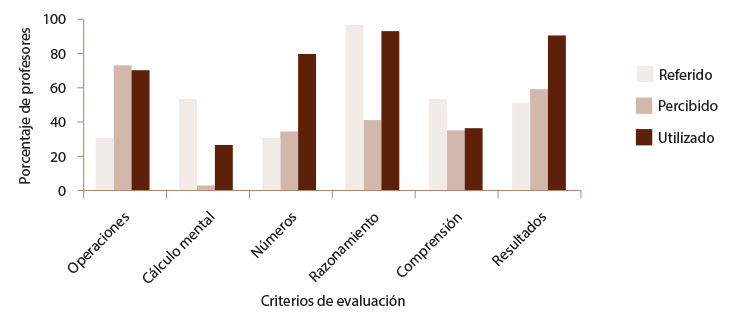
Nota: Elaboración propia.
El índice de Jaccard, que mide la convergencia entre los criterios referidos por cada profesor y los que utilizó posteriormente en la actividad de evaluación ciega varía entre 0 y 0,75 (X=0,38; DT=0,18). Solo 9 de 30 docentes obtuvieron valores superiores a 0,50, lo que sugiere una cierta discrepancia entre los criterios de evaluación referidos y utilizados en la mayoría de la muestra de profesorado.
El índice que cuantifica la convergencia entre los criterios percibidos por el alumnado y los utilizados por el profesorado en la evaluación ciega varía entre un mínimo de 0 y un máximo de 0,8. El promedio fue, en este caso, 0,35 y la desviación típica 0,15; lo que refleja también una clara discrepancia.
Diferencias en función del curso académico
En cuanto al curso académico en que impartía docencia el profesorado, no se encontraron diferencias significativas en cuanto a los criterios referidos en las entrevistas por el profesorado de 2º y de 4º curso. Tampoco se encontraron diferencias significativas en cuanto a los criterios utilizados en la evaluación ciega, salvo en las categorías reducciones (X2=7,77; p<0,01), más frecuentemente utilizado en 4º curso; y automatización técnicas (X2=6,53; p=0,01), más utilizado en 2º. En cuanto al grado de convergencia no hay una diferencia significativa entre el promedio de los índices de Jaccard obtenidos en la muestra de profesorado de 2º (X=0,42; DT=0,21) y la de 4º (X=0,35; DT=0,17).
En cambio, el porcentaje de alumnos de 2º curso que aludió a cada criterio fue mucho menor que el porcentaje de alumndo de 4º (salvo en escritura de números, donde no hay una diferencia significativa). También resultó más bajo el promedio de los resultados del índice de Jaccard (X=0,30; DT=0,17), en comparación con el de 4º (X=0,41; DT=0,24). Dicho de otro modo, la convergencia de la percepción de los alumnos de 2º con respecto a los criterios realmente utilizados por sus docentes es menor que el del alumnado de 4º (Figura 2). La prueba t de Student confirmó que se trata de una diferencia significativa (t=2,87; p=0,005).
Figura 2: Promedios de los índices de convergencia de criterios (índice Jaccard) obtenidos en la muestra de profesorado y alumnado de 2º y 4º curso
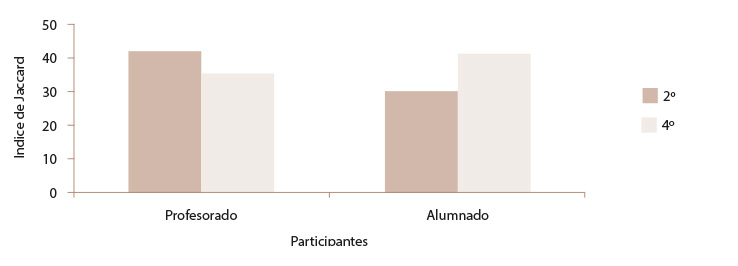
Nota: Elaboración propia.
Diferencias de percepción del alumnado en función del rendimiento académico
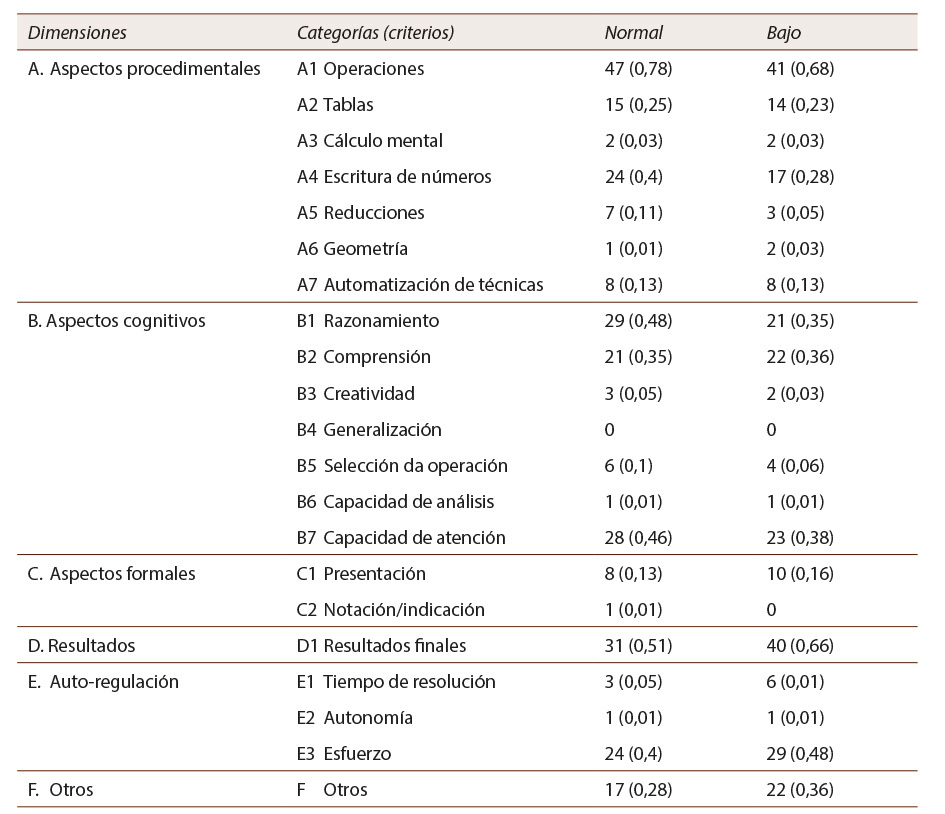
En cuanto al rendimiento académico, por último, la Tabla 3 muestra una coincidencia en la percepción del alumnado con medio y bajo rendimiento al considerar las operaciones aritméticas y los resultados finales como los criterios de evaluación más importantes para conseguir una buena calificación en matemáticas.
Las diferencias entre el porcentaje de estudiantes con rendimiento normal vs. bajo que mencionaron (al menos una vez) cada criterio de evaluación no resultó estadísticamente significativa.
Tabla 3: Frecuencia y porcentaje de aparición de las categorías de criterios de evaluación en la entrevista a estudiantes (criterios percibidos) en función del rendimiento académico (normal o bajo)
Nota: Elaboración propia.
Discusión
Los resultados anteriores nos aportan información útil acerca de la diversidad del pensamiento del profesorado de la educación primaria sobre los criterios de evaluación de tareas matemáticas. Las categorías criteriales, referidas a los aspectos cognitivos que el profesorado verbalizó durante las entrevistas (Tabla 1) reflejan claramente 4 de los 6 elementos competenciales propuestos por la OCDE, que desglosábamos en la introducción de este trabajo: (1) la comprensión y comunicación de enunciados con información matemática (criterio B2 en la tabla 1); (3) la matematización o traslación a modelos matemáticos de situaciones problemáticas (criterios B4 y B6); (5) la selección y utilización de estrategias para resolver problemas matemáticos (criterio B5); (6) el razonamiento y la argumentación matemática (criterio B1).
Apenas se detectan diferencias significativas entre el personal docente de 2º y 4º curso de Educación Primaria. Recordemos que casi todo el profesorado otorgó mucha importancia, no solo a la corrección de las operaciones aritméticas y al resultado final, sino también a criterios de índole cognitiva-procesual, relacionados principalmente con el razonamiento matemático, es decir, con la realización de inferencias lógicas basadas en conectar elementos de problemas para justificar las operaciones o conclusiones matemáticas (Turner et al., 2015). Este criterio de evaluación fue, de hecho, el único que el profesorado refirió explícitamente en las entrevistas y utilizó realmente en la actividad de evaluación. Sin embargo, de acuerdo con las medidas obtenidas en el índice de Jaccard, en torno a un tercio del personal docente, muestra una significativa discrepancia entre el resto de criterios que refierieron en las entrevistas y lo que realmente utilizaron en la actividad de evaluación ciega. En particular, más de un 40% de participantes que no mencionaron la escritura de números, los algoritmos aritméticos y la corrección del resultado final de los problemas como criterios de evaluación relevantes, los utilizaron posteriormente en la actividad de evaluación ciega (Figura 1).
En cuanto al alumnado, no hemos encontrado una percepción significativamente diferente en función del rendimiento académico. En cambio, en función del curso, el alumnado más inmaduro (de ٢º) menciona, en las entrevistas, un número significativamente menor de criterios que los de 4º; lo que sugiere una escasa conciencia de las diversidad de elementos que se pueden tener en cuenta en la evaluación. Esto explicaría por qué, de acuerdo con el índice de Jaccard, obtenido como promedio en la muestra de 2º, la discrepancia entre los criterios percibidos por el alumnado y utilizado por el profesorado en este nivel educativo es mayor que en 4º curso (Figura 2).
En conjunto, a diferencia de sus docentes, solo una minoría del estudiantado coincide en percibir que el razonamiento matemático tiene un peso significativo en las calificaciones de sus ejercicios. Para la gran mayoría, lo más importante es la corrección de las operaciones y algoritmos aritméticos. Casi la mitad del alumnado entrevistado considera también que la concentración o el esfuerzo tienen un peso muy relevante en las calificaciones, y un 15% le otorga mucha importancia a la presentación formal de los ejercicios.
Conclusiones
En definitiva, podemos extraer dos conclusiones principales de estos resultados. Por un lado, los datos obtenidos en las entrevistas y en la actividad de evaluación ciega ponen de manifiesto que casi todo el profesorado que participó en el estudio considera importante evaluar las tareas matemáticas, no solo en función de la corrección de las operaciones aritméticas y los resultados de los problemas, sino también según criterios procesuales relacionados con la comprensión de los enunciados y el razonamiento matemático. Además, el profesorado tiene también mayoritariamente en cuenta dichos criterios de comprensión y razonamiento a la hora de calificar una prueba de evaluación.
Esta conclusión contrasta con lo encontrado por Rosales et al. (2012) en actividades de evaluación de problemas aritméticos en la educación primaria. El análisis de la interacción verbal en dichas actividades mostró que la mayoría del profesorado tendía a afrontar este tipo de tarea de un modo paradigmático y superficial, es decir, centrándose más en la resolución mecánica de los algoritmos que en la comprensión situacional de los problemas y en los procesos de autorregulación. Nuestra investigación evidencia, por el contrario, la preocupación del profesorado por evaluar la comprensión y la toma de decisiones sobre las operaciones para resolver un problema matemático, aunque no tanto por evaluar y apoyar los procesos de autorregulación. La información más útil para potenciar la autonomía del alumnado es aquella, de carácter cualitativo, que facilita que tome consciencia de lo que necesitan afianzar o corregir: lo que hacen bien y lo que puede mejorar. En este sentido, la consideración de criterios relacionados con valorar la capacidad del alumnado de co-evaluar y autorregular sus propias tarea es fundamental para conseguir una auténtica evaluación formativa (Clark, 2012). Aunque la actividad de evaluación ciega no facilita que el profesorado utilice este tipo de criterios, tampoco fueron mencionados por el profesorado o el alumnado en las entrevistas.
Por otro lado, la discrepancia encontrada entre los criterios referidos por un tercio aproximadamente del personal docente en las entrevistas, los percibidos por sus estudiantes y los realmente utilizados en la actividad de evaluación ciega sugiere una insuficiente conciencia de buena parte del profesorado acerca de los criterios que realmente tienen en cuenta en sus actividades de evaluación, así como la necesidad de clarificarlos mejor a su alumnas y alumnos. La comprensión de los criterios por parte del alumnado tiene un importante impacto en la evaluación del aprendizaje (Amigues y Guignard-Andreucci, 1981; Barbosa y Alaíz, 1994; No se trata simplemente de comunicar con precisión qué y cómo se va a evaluar al alumnado. Más allá de la evaluación formativa, se ha reclamado la importancia de promover una evaluación formadora haciendo partícipe a niñas y niños de la concreción y aplicación de los criterios de evaluación; no únicamente como objeto de la evaluación, sino también como sujeto activo del proceso de evaluación desde su inicio. Dicha evaluación formadora es especialmente necesaria en el alumnado más maduro (a partir de los 9 o 10 años); dado que, como se desprende de los resultado de este estudio, por debajo de esa edad los niños y las niñas manifiestan una escasa consciencia de la diversidad de criterios de evaluación del aprendizaje de las matemáticas.
Nuestros resultados tienen, en definitiva, importantes implicaciones que pueden orientar la formación permenente del profesorado en esta área curricular. Parece necesario, especialmente, potenciar una reflexión sobre la distancia entre el pensamiento y la acción docente en el ámbito de la evaluación del aprendizaje de las matemáticas: entre la consciencia sobre los criterios que se consideran más relevantes y su aplicación en las actividades de evaluación. Únicamente revisando nuestra propia práctica podremos acortar esa distancia para, por un lado, mejorar los instrumentos y decisiones que tomamos durante la evaluación, y, por otro, conseguir una evaluación auténticamente formadora.
Limitaciones y prospectiva
Cabe señalar, finalmente, algunas cuestiones, relativas a la naturaleza de las tareas y el procedimiento de evaluación empleados en la presente investigación, que obligan a considerar con cautela las anteriores conclusiones. Como en muchas otras investigaciones similares, los procedimientos de entrevista y autoinforme del profesorado están fuertemente amenazados por un sesgo de deseabilidad social, que podría haber influido en la preponderancia de los criterios relacionados con la comprensión y el razonamiento matemático.
No cabe duda, además, de la artificialidad de la actividad de evaluación ciega. El hecho de que al personal docente no se le permitiera elaborar la prueba de evaluación, y que el estudiantado que la realizó no estuviera presente, ha podido influir en la desatención de ciertos criterios de evaluación formativa, principalmente los relativos a la autorregulación. La actividad que se recrea en esta situación experimental se parece a los exámenes de orientación sumativa, que una parte del profesorado emplea a veces sin considerar otros tipos de criterios de evaluación en el conjunto del proceso de enseñanza y aprendizaje.
Una última limitación tiene que ver con el sistema de categorías empleado para clasificar los criterios de evaluación. Algunos criterios, como la escritura de números o las tablas de multiplicar, están claramente condicionados por los contenidos curriculares propios de estos niveles educativos. El razonamiento matemático, por su parte, es un criterio difícil de diferenciar de otros conceptos adyacentes. El alumnado, e incluso el propio profesorado, tiene dificultades para conceptualizar con precisión este tipo de criterios; lo que podría explicar la discrepancia de su percepción con respecto al profesorado.
En futuras investigaciones convendría, por tanto, revisar y operativizar mejor este tipo de categorías, con muestras de profesorado y alumnado de otros niveles educativos de la educación primaria.
Declaración de contribuciones:
Las personas autoras declaran que han contribuido en los siguientes roles: M. J. M. O. contribuyó con la escritura de la versión postulada del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación. M. M. contribuyó con la escritura de la versión postulada del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación.
Declaración de Material complementario
Este artículo tiene disponible, como material complementario:
-La versión preprint del artículo en https://doi.org/10.5281/zenodo.5517795
Referencias
Alves Martins, M., Matta, I., Mata, L. y Nunes, C. (1991). Avaliação em língua materna e matemática do 1.º ciclo do ensino básico: Critérios referidos e utilizados por professores e percepcionados por alunos com sucesso e insucesso escolar. Análise Psicológica, 9 (3-4), 453-466. http://repositorio.ispa.pt/bitstream/10400.12/5213/1/AP-1991_34_453.pdf
Amigues R. y Guignard-Andreucci, C. (1981). A propos d’une recherche sur l’évaluation formative en situation éducative: prise en compte et modifications des donnés de la situation. Bulletin de Psychologie, (353), 167-172.
Barbosa, J. y Alaíz, V. (1994). Explicitação de critérios - exigência fundamental de uma avaliação ao serviço da aprendizagem. En Pensar a avaliação, melhorar a aprendizagem (pp. 1-5). Instituto de Inovação Educacional. http://docplayer.com.br/19644130-Explicitacao-de-criterios-exigencia-fundamental-de-uma-avaliacao-ao-servico-da-aprendizagem.html
Black, P. y Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy & Practice, 5(1), 7-73. https://doi.org/10.1080/0969595980050102
Black, P. y Wiliam, D. (2009). Developing the theory of formative assessment. Educational Assessment, Evaluation and Accountability, 21(1), 5-31. https://doi.org/10.1007/s11092-008-9068-5
Bonniol, J. J. (1986). Recherches et formations: Pour une problématique de l’évaluation formative. En J.-M. De Ketele (Ed), L’évaluation: Approche descriptive ou prescriptive? (pp. 119-133). De Boeck.
Clark, I. (2012). Formative assessment: Assessment is for self-regulated learning. Educational Psychology Review, 24(2), 205-249. https://doi.org/10.1007/s10648-011-9191-6
Coll, C., Barberà, E. y Onrubia, J. (2000). La atención a la diversidad en las prácticas de evaluación. Infancia y Aprendizaje, 23(90), 111-132 https://doi.org/10.1174/021037000760087991
De Ory Azcárate, M. y Ruiz Suárez, V. M. (2011). La evaluación en el aula de primaria. Factor clave para el aprendizaje de las ciencias y las matemáticas. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias 8(2), 212-220. https://doi.org/10.25267/Rev_Eureka_ensen_divulg_cienc.2011.v8.i2.08
Hadji, C. (2001). Avaliação desmistificada. Artmed Editora.
Jaccard, P. (1901). Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bulletin de la Société Vaudoise des Sciences Naturelles, 37(140), 241-272. https://www.researchgate.net/publication/243457811_Distribution_de_la_Flore_Alpine_dans_le_Bassin_des_Dranses_et_dans_quelques_regions_voisines
Kintsch, W. y Greeno, J. (1985). Understanding and solving word arithrmetic problem. Psychological Rewiev, 92(1), 109-129. https://doi.org/10.1037/0033-295X.92.1.109
Melo, M. y Veiga, F. H. (2013). Aprendizagem: Perspetivas socioconstructivistas. En F. H. Veiga, (Coord.), Psicologia da educação: Teoria, investigação e aplicação: Envolvimento dos alunos na escola (pp. 263-296). Climepsi.
Montanero, M. (2019). 4 criterios e instrumentos de evaluación. En M. Montanero (Autor), Didáctica general. Planificación y práctica de la enseñanza primaria (pp. 64-94). Servicio de publicaciones de la UEx. http://dehesa.unex.es/bitstream/10662/9225/1/978-84-09-07197-5.pdf
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Autor.
Noizet, G. y Caverni, J.-P. (1985). Psicologia da avaliação escolar. Coimbra.
Nunes, C. (1990). Avaliação de textos escritos: Critérios referidos e utilizados pelos professores e a sua percepção por alunos com diferente estatuto escolar [Tesis de maestría, Instituto Superior de Psicologia Aplicada]. https://repositorio.ispa.pt/handle/10400.12/736
Onrubia, J. y Lago, J.-R (2008). Asesoramiento psicopedagógico y mejora de las prácticas de evaluación. Infancia y Aprendizaje, 31(3), 363-383. https://doi.org/10.1174/021037008785702929
Organization for Economic Coopeation and Development. (2013). PISA 2012 assessment and analytical framework. Mathematics, reading, science, problem solving and financial literacy. Autor. https://doi.org/10.1787/9789264190511-en
Pacheco, J. A. (2002). Critérios de avaliação na escola. En Ministério da Educação (Ed.), Avaliação das aprendizagens: das concepções às práticas (pp. 53-64). Departamento da Educação Básica.
Pinto, J. y Santos, L. (2006). Modelos de avaliação das aprendizagens. Universidade Aberta.
Riggan, M. y Nabors Oláh, L. (2011). Locating interim assessments within teachers’ assessment practice. Educational Assessment, 16(1), 1-14. https://doi.org/10.1080/10627197.2011.551085
Rosales, J., Vicente, S., Chamoso, J. M., Muñez, D. y Orrantia, J. (2012). Teacher-estudent interaction in joint word problem solving. The role of situational and mathematical knowledge in mainstream classrooms. Teaching and Teacher Education, 28(8), 1185-1195. https://doi.org/10.1016/j.tate.2012.07.007
Sanmartí, N. (2007). 10 ideas clave: Evaluar para aprender. Graó.
Struyven, K., Dochy, F. y Janessens, S. (2005). Students’ perceptions about evaluation and assessment in higher education: a review. Assessment & Evaluation in Higher Education, 30(4), 325-341. https://doi.org/10.1080/02602930500099102
Suurtamm, C., Koch, M. y Arden, A. (2010). Teachers’ assessment practices in mathematics: Classrooms in the context of reform. Assessment in Education: Principles, Policy & Practice, 17(4), 399-417. https://doi.org/10.1080/0969594X.2010.497469
Teledahl, A. (2015). Different modes in teachers’ discussions of students’ mathematical texts. Teaching and Teacher Education, 51, 68-76. https://doi.org/10.1016/j.tate.2015.06.002
Turner, R., Blum, W. y Niss, M. (2015). Using competencies to explain mathematical item demand: Awork in progress. En K. Stacey y R. Turner (Eds.), Assessing mathematical literacy: The PISA experience (pp. 85-115). Springer. https://doi.org/10.1007/978-3-319-10121-7_4
Veldhuis, M., van den Heuvel-Panhuizen, M., Vermeulen J. A. y Eggen, T. J. H. M. (2013). Teachers’ use of classroom assessment in primary school mathematics education in the Netherlands. Cadmo, 21(2), 35-53. https://www.researchgate.net/publication/260095083_Teachers%27_Use_of_Classroom_Assessment_in_Primary_School_Mathematics_Education_in_the_Netherlands
Selter, C. Verschaffel, L., Greer, B. y de Corte, E. (2000). Making sense of word problems. Educational Studies in Mathematics, 42(2), 211–213. https://doi.org/10.1023/A:1004190927303

Artículo de la Revista Electrónica Educare de la Universidad Nacional, Costa Rica by Universidad Nacional is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Costa Rica License.
Based on a work at https://www.revistas.una.ac.cr/index.php/EDUCARE
Permissions beyond the scope of this license may be available at educare@una.ac.cr
