Revista Electrónica Educare (Educare Electronic Journal) EISSN: 1409-4258 Vol. 27(1) ENERO-ABRIL, 2023
doi: https://doi.org/10.15359/ree.27-1.14302
https://www.revistas.una.ac.cr/index.php/educare
educare@una.ac.cr
[Cierre de edición el 01 de Enero del 2023]
Actitudes hacia la matemática en futuro personal docente del área: Adaptación colombiana de la escala EAHM-U
Attitudes Towards Mathematics in Future Teachers: EAHM-U Scale Colombian Adaptation
Atitudes em relação à matemática em futuros professores da área: Adaptação colombiana da escala EAHM-U
Universidad del Atlántico
Barranquilla, Colombia
joseavila@mail.uniatlantico.edu.co
 https://orcid.org/0000-0002-2913-1528
https://orcid.org/0000-0002-2913-1528
Leonardo José Vargas-Delgado
Universidad del Atlántico
Barranquilla, Colombia
ljvargas@mail.uniatlantico.edu.co
 https://orcid.org/0000-0002-9014-1418
https://orcid.org/0000-0002-9014-1418
Marien Fernanda Alonso-Miranda
Universidad del Atlántico
Barranquilla, Colombia
mfalonso@est.uniatlantico.edu.co
 https://orcid.org/0000-0002-3251-5936
https://orcid.org/0000-0002-3251-5936
Jean Carlos De La Cruz-González
Universidad del Atlántico
Barranquilla, Colombia
jeancdelacruz@est.uniatlantico.edu.co
 https://orcid.org/0000-0002-2203-4995
https://orcid.org/0000-0002-2203-4995
Recibido • Received • Recebido: 03 / 08 / 2020
Corregido • Revised • Revisado: 26 / 10 / 2022
Aceptado • Accepted • Aprovado: 14 / 11 / 2022
Resumen:
Introducción. Las actitudes positivas y negativas influyen en los procesos de enseñanza-aprendizaje de las matemáticas, por lo cual este estudio se enfocó en analizar las propiedades psicométricas que presenta la “Escala de actitudes hacia la matemática (EAHM-U)” en estudiantado universitario colombiano con el fin de proporcionar una herramienta de medición ajustada al contexto y debidamente validada. Metodología. Mediante un diseño instrumental con 446 estudiantes de licenciatura en matemáticas se analizó la estructura factorial y la consistencia interna de las puntuaciones del instrumento. Resultados. Se obtuvo un instrumento de 13 ítems con dos dimensiones denominadas beneficio de la matemática y dificultad en el aprendizaje de la matemática. Discusión. La escala modificada presenta adecuadas calidades psicométricas, niveles favorables de fiabilidad en las puntuaciones e indicadores de replicabilidad que sugieren que los reactivos miden apropiadamente cada dimensión.
Palabras claves: Actitudes hacia las matemáticas; docentes; enseñanza-aprendizaje; cuestionario.
Abstract:
Introduction. Positive and negative attitudes influence the teaching-learning processes of mathematics, so this study focused on analyzing the psychometric properties of the Attitudes Toward Mathematics Scale (EAHM-U) in Colombian university students to provide a context-adjusted and truly validated measurement tool. Method. An instrumental design was used with 446 undergraduate mathematics students to analyze the factor structure and internal consistency of the instrument scores. Results. a 13-item instrument with two dimensions called benefit from mathematics and difficulty in learning mathematics was obtained. Discussion. The modified scale presents adequate psychometric qualities, favorable levels of reliability in the scores, and indicators of replicability, suggesting that the items measure each dimension appropriately.
Keywords: Attitudes towards mathematics; teachers; teaching-learning; questionnaire.
Resumo:
Introdução. Atitudes positivas e negativas influenciam os processos de ensino-aprendizagem da matemática, portanto, este estudo se concentrou na análise das propriedades psicométricas da Escala de Atitudes em Matemáticas (EAHM-U) em estudantes universitários colombianos para fornecer uma ferramenta de medição ajustada ao contexto e devidamente validada. Metodologia. Utilizando um desenho instrumental com 446 estudantes de matemática de graduação, foi analisada a estrutura dos fatores e a consistência interna das pontuações dos instrumentos. Resultados. Um instrumento de 13 itens com duas dimensões chamadas benefício da matemática e dificuldade em aprender matemática foi obtido. Discussão. A escala modificada apresenta qualidades psicométricas adequadas, níveis favoráveis de confiabilidade nos escores e indicadores de replicabilidade que sugerem que os itens medem cada dimensão adequadamente.
Palavras-chave: Atitudes em relação à matemática; professores; ensino-aprendizagem; questionário.
Introducción
El dominio afectivo ha sido aceptado como un importante constructo en educación matemática y estadística, pues se considera que, al igual que los aspectos cognitivos, aquellos de naturaleza afectiva influyen en el proceso de enseñanza y aprendizaje (Casas-Rosal et al., 2018). Un elemento importante de este dominio lo constituyen las actitudes, entendidas como las creencias y la carga afectiva que tiene el estudiantado hacia los contenidos matemáticos y que pueden influir en la aproximación positiva o el rechazo por el área (Casis et al., 2017; Mejía Saldaña et al., 2018).
La investigación sobre el tema ha mostrado que las personas que se sienten incapaces de aprender matemáticas crean actitudes negativas que bloquean el aprendizaje (Estrada Roca y Diez-Palomar, 2011), entre más negativas sean más deficiente es el desempeño (Duarte-Sepúlveda et al., 2018). Opuestamente, entre el estudiantado con actitud positiva que percibe las matemáticas como útiles, se registran niveles más elevados de comprensión y también alta confianza en el aprendizaje del área (Cerda et al., 2016).
Sin embargo, la mayoría de los estudios han privilegiado los niveles educativos básico y medio, y son menos comunes los trabajos en educación superior (Ramírez Cruz et al., 2018), especialmente con futuros maestros y maestras. Abordar el componente actitudinal del personal docente en formación merece toda la atención, dado que el maestro y la maestra generan una poderosa influencia desde los niveles iniciales de formación en niños y niñas, por lo que su respuesta afectiva influye decisivamente en la construcción de actitudes en el alumnado (Gamboa Araya y Moreira-Mora, 2017).
Medición de las actitudes hacia las matemáticas
Los instrumentos diseñados para evaluar las actitudes hacia la matemática son diversos (Tabla 1) y en general sus fundamentos teóricos reconocen que se trata de un proceso multidimensional. Las dimensiones comúnmente relacionadas con la medición de las actitudes se enfocan en la experiencia de agrado hacia la matemática (Aiken y Dreguer, 1961; Aparicio y Bazán, 1997; Auzmendi Escribano, 1992; Michaels y Forsyth, 1977), así como su opuesto, representado en diversos instrumentos como respuesta de ansiedad (Aparicio y Bazán, 1997; Igualmente, otro factor común en los instrumentos disponibles consiste en el nivel de comprensión del estudiantado hacia los contenidos de esta disciplina, y también en su parecer acerca de cuán útiles son dichos conocimientos
Por otro lado, aunque la generación de cuestionarios sobre el tema data de la década de 1960, los primeros aportes a la cuestión en idioma español solo se dieron hasta la década de 1990, y desde allí ha crecido el número de pruebas disponibles. Desafortunadamente, en Colombia no se cuenta con un amplio inventario de instrumentos fiables en las distintas áreas del conocimiento, y menos aún en educación matemática, donde la tradición investigativa internacional es eminentemente cualitativa. La alternativa para las investigaciones consiste en recurrir a instrumentos realizados en otros contextos, la mayor parte de estos tienen el inconveniente de ser realizados en inglés, otros, aunque publicados en español se enfocan en poblaciones puntuales como estudiantes de secundaria y bachillerato (Palacios et al., 2014; y son pocos los que se desarrollan en nivel superior.
Tabla 1: Instrumentos para la medición de actitudes hacia las matemáticas
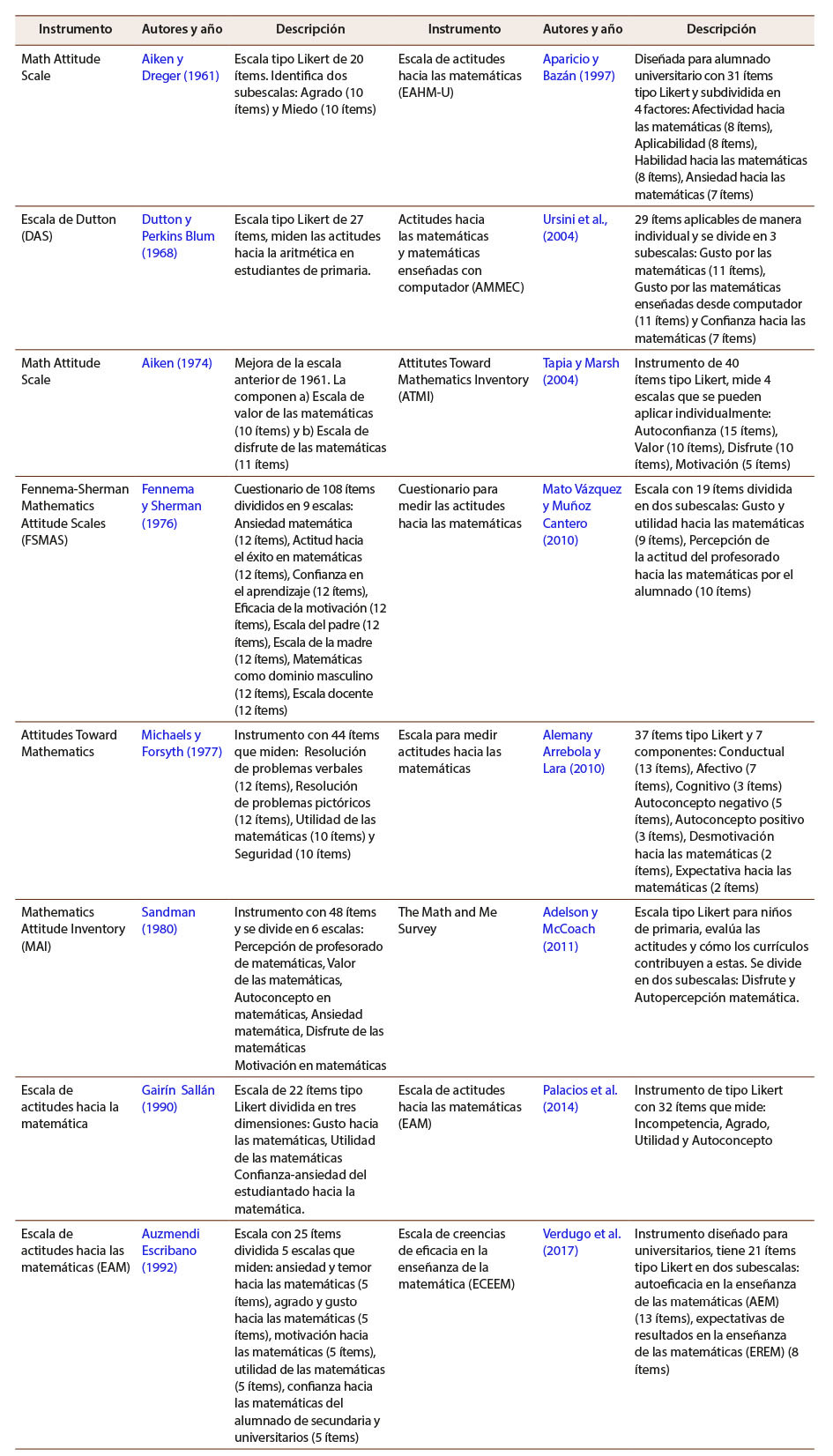
Nota: Elaboración propia.
Recientemente Rodríguez Jiménez y Mora Mojica (2016) realizaron la validación de un cuestionario que identifica las actitudes hacia las matemáticas en estudiantado colombiano partiendo de varias revisiones previas a la EAHM-U de Aparicio y Bazán (1997), tales revisiones consisten en un par de trabajos de maestría que incluyen el de una de las autoras, Mora. En estos, todos los ajustes realizados al instrumento original condujeron a una versión unidimensional obtenida por medio del análisis factorial confirmatorio.
Sin embargo, el análisis multifactorial original del EAHM-U obedece a una organización consistente y de buen comportamiento psicométrico que puede ser más enriquecedor en la investigación sobre el tema. Adicionalmente, la revisión realizada muestra que el estudio de las actitudes hacia la matemática se enfoca en la actitud del estudiantado y en algunas ocasiones incluye su reporte sobre el rol del personal docente, pero no se cuenta con adaptaciones instrumentales que aborden el papel actitudinal en futuros cuerpos educativos de matemáticas, por lo cual el desarrollo de este estudio es especialmente útil.
Este instrumento debidamente adaptado para esa futura población, y con criterios propicios de fiabilidad y validez en el contexto colombiano, puede convertirse en una herramienta importante para la investigación en dominio afectivo del país desde la formación inicial docente, a la luz de que la bibliografía de años recientes refuerza la necesidad de evaluar el efecto de las actitudes y las creencias hacia la matemática sobre la forma como asumen la disciplina quienes se convertirán en profesores y profesoras del área (Ingram et al., 2020). Así como se reconoce que esta población puede expresar ideas que autolimitan su aprendizaje, o atribuir la experiencia de aprendizaje escolar de la matemática a actitudes de dificultad, escasa utilidad, aburrimiento y sentimientos de miedo o desagrado (Itter y Meyers, 2017), también es factible fomentar actitudes positivas incluso en quienes se perciben con baja capacidad académica, promoviendo el esfuerzo y el desarrollo de actividades que generan mentalidad de crecimiento (Tran y Javed, 2017).
Las implicaciones investigativas son amplias, y las aplicaciones de la escala para múltiples estudios que aborden el dominio afectivo en personal docente en preservicio también representan un aliento para trabajar en la adaptación instrumental. Por ello este estudio ha sido desarrollado con el objetivo de analizar las propiedades psicométricas del EAHM-U en pro de obtener adaptación para futuro personal educador de matemática.
Método
Diseño
Se desarrolló un estudio de tipo instrumental cuya lógica se basa en evaluar las propiedades psicométricas de instrumentos de medición, para lo cual se recomienda ajustarse a los protocolos internacionales que definen estándares de validación de escalas desarrollados por American Educational Research Association (AERA), American Psychological Association (APA) y National Council on Measurement in Education (NCME).
Participantes
La población la constituye el estudiantado de Licenciatura en Matemáticas de una universidad pública colombiana cuya cursada es de cuatro años divididos en dos semestres académicos cada uno. La muestra la representaron 446 estudiantes con edades comprendidas entre 17 y 25 años (M=21,07, de=2,2), 257 hombres (n=57,2%) y 192 mujeres (42,8%) de primer a octavo semestre.
Instrumentos
El Cuestionario actitudes hacia las matemáticas (EAHM-U) fue diseñado para ser aplicado con estudiantado universitario de diferentes programas académicos, cuenta con 31 preguntas tipo Likert (1= totalmente en desacuerdo, 5= totalmente de acuerdo) que evalúan cuatro dimensiones: habilidad, ansiedad, afectividad y aplicabilidad.
Las cuatro dimensiones miden aspectos distintos en el estudiantado, la dimensión de afectividad da como resultado el sentimiento de agrado o desagrado hacia la asignatura, la dimensión de aplicabilidad da a conocer la utilidad percibida de la disciplina, la dimensión de habilidad refleja las destrezas que el estudiantado considera tener para resolver ejercicios matemáticos y mide la confianza que tiene en sus conocimientos, por último, la dimensión de ansiedad da a conocer sus diferentes reacciones emocionales hacia problemas matemáticos. Las tres primeras dimensiones se componen de ocho ítems y la última cuenta con siete. De todos esos reactivos, 18 están formulados en sentido positivo y 13 tienen puntuación inversa. La división de los ítems del instrumento aceptados por dimensiones y la estructura en la que están formulados (positivos - negativos) pueden apreciarse en la Tabla 2.
Tabla 2: Dimensiones e ítems de la escala de Actitudes hacia las matemáticas (EAHM-U)
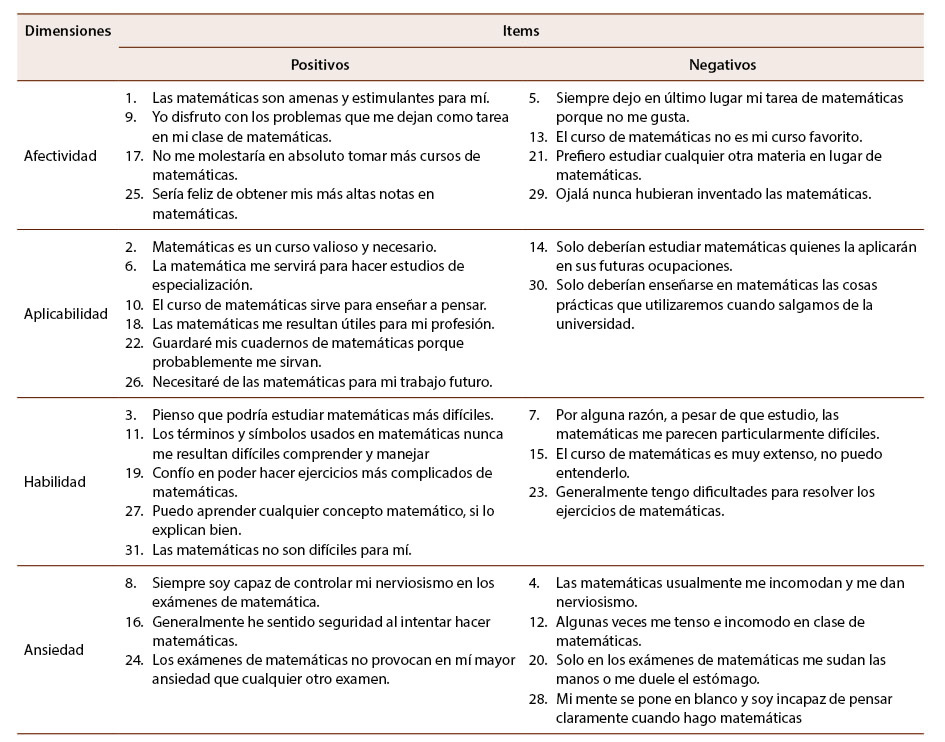
Nota: Elaboración propia.
Las puntuaciones del instrumento reportan buenos niveles de fiabilidad con coeficientes alpha de Cronbach de .764 para la subescala afectividad, .760 para aplicabilidad, .780 para la subescala habilidad, .712 para ansiedad, y un coeficiente global de .906. Estas subescalas también muestran coeficientes de correlación significativos entre ellas, de esta forma, afectividad expresa correlación de .60, .67 y .57 con las demás subescalas, aplicabilidad ofrece coeficientes de .51 y .47, y finalmente habilidad y ansiedad tienen un coeficiente de correlación de .72.
Procedimiento
La aplicación del instrumento se desarrolló entre los meses de marzo y julio de 2019 con diferentes grupos de estudiantes. El proceso se cumplió de forma grupal y autoadministrada contando siempre con un sujeto investigador que orientó en todos los aspectos necesarios. El llenado del instrumento fue anónimo, solo se requirió de información demográfica como sexo, edad y el semestre académico. En todos los casos los sujetos participantes ofrecieron su consentimiento voluntario para ser parte del estudio. Tras la recogida de los datos, fueron cargados en una base construida en Excel y posteriormente exportada al software FACTOR (v. 10.10.02) (Lorenzo-Seva y Ferrando, 2006) con el cual se realizó el análisis del instrumento.
Análisis de datos
Una vez construida la base se identificaron valores perdidos, por lo cual se aplicó el procedimiento de imputación de datos. Corregida la base, se efectuó análisis factorial multivariado para comprobar el supuesto de normalidad con el coeficiente multivariante de Mardia; posteriormente, se optó por calcular la matriz de correlación entre las variables empleando correlaciones policóricas en lugar del método tradicional de Pearson, esto en función de que la escala de medición responde a gradación tipo Likert, por lo cual el método policórico es el más apropiado y supera las limitaciones que implica tratar las variables como si fueran continuas.
Esta misma razón condujo a que se escogiera el análisis paralelo (AP) como procedimiento para definir el número de factores, dado que la regla tradicional de Kaiser (eigenvalor ≥ 1), a pesar de ser la de mayor difusión, tiende a sobre o infradimensionar la solución factorial cuando el análisis se cumple con ítems politómicos. Se emplearon los mínimos cuadrados no ponderados robustos (Robust Unweighted Least Squares- RULS) como método de estimación de factores dado que es de mucha utilidad en la factorización de matrices aún en situaciones adversas al no tener la necesidad de responder a supuestos de distribución (Lloret-Segura et al., 2014), por su parte, la rotación se cumplió con el método Promin (Lorenzo-Seva, 1999).
Siguiendo las recomendaciones para los estudios psicométricos actuales (Lloret-Segura et al., 2014), se aplicaron criterios que permiten identificar la validez de la solución factorial obtenida mediante el AP, para ello se calculó la raíz media cuadrática residual (RMCR) que identifica la magnitud media de las correlaciones residuales, valores inferiores a .05 se consideran apropiados. También se calculó el índice de bondad de ajuste (GFI) que señala qué proporción de la varianza entre los ítems analizados es explicada por el modelo propuesto. Esta medida toma valores que van de 0 a 1 y se considera que valores superiores a .95 indican buen ajuste. La tercera medida calculada fue el error cuadrático medio de aproximación por grado de libertad (RMSEA), basada en Chi cuadrado y, por ende, se relaciona con los grados de libertad del modelo; se considera que valores inferiores a .05 son excelentes y aun aquellos valores que no superan .08 son admisibles.
Para determinar las medidas de confiabilidad de las puntuaciones se calculó el coeficiente omega de McDonald, adicionalmente, se calculó el índice H generalizado (G-H) (Ferrando y Lorenzo-Seva, 2018) que evalúa la medida en que el conjunto de elementos representa de forma apropiada un factor común. Este índice toma valores entre 0 y 1 y aquellos valores >.80 sugieren que la variable se encuentra bien definida. Complementariamente se calculó la calidad y efectividad de las estimaciones de puntuación de factores (Ferrando y Lorenzo-Seva, 2018) a través de cuatro medidas: Índice de determinación del factor (Factor Determinacy Index - FDI), confiabilidad marginal de ORION (Overall Reliability of fully-Informative prior Oblique N-EAP scores/fiabilidad general de las puntuaciones oblicuas N-EAP completamente informativas), ratio de sensibilidad (Sensitivity Ratio - SR) y el porcentaje esperado de diferencias verdaderas (Expected percentage of true differences - EPTD).
Resultados
En el análisis inicial de patrón de valores muestrales se observó que 10 variables (ítems del instrumento) presentaron valores perdidos, lo que equivale a 32,3% de las variables analizadas; esas ausencias de datos se registraron en solo 13 participantes (2,9%) y correspondieron en total a 14 valores de los 13 919 registrados en la base. Se procedió a cumplir la imputación empleando las variables de cada dimensión como indicador para los ítems a imputar.
Análisis factorial para un modelo de cuatro factores
Tras la corrección de la base se realizó la exploración de las características distributivas de los datos donde se observó que el análisis descriptivo multivariado siguiendo la regla de Mardia mostró datos significativos (asimetría=274.550, curtosis=1271.578, p=.001<.05). Se procedió a realizar análisis factorial exploratorio siguiendo la propuesta original de cuatro dimensiones formulada por los autores del instrumento, en este caso los valores de adecuación de la matriz de correlaciones policóricas obtuvieron niveles mínimos (justa) (Bartlett = 5029,2, p= .001<.05; KMO = 0,76).
La extracción factorial, por su parte, se cumplió con la versión de análisis robusto de mínimos cuadrados no ponderados (RULS), y condujo a eliminar los ítems 16 y 30 por poseer cargas absolutas inferiores a .30. Adicionalmente, este modelo dejó observar que los ítems responden a una organización factorial diferente a las cuatro dimensiones originalmente presentadas por la EAHE-U, infiriéndose que la estructura factorial en la población de análisis es sustancialmente distinta, prueba de que la elección de análisis factorial exploratorio en lugar del confirmatorio fue acertada. En esta solución factorial se identifican siete ítems (2,4,5,9,14,19,21) que cargan a más de un factor, algunos de ellos con cargas relativamente similares para los diferentes factores. Frente a ello, la revisión de resultados del análisis paralelo (AP) basado en un análisis factorial de rangos mínimos sugirió que el número de dimensiones recomendadas era de 2.
Adicionalmente, el análisis robusto para identificar criterios de bondad de ajuste reportó valores RMSR de .056 que se eleva sutilmente frente al valor crítico (.05), en cambio el error cuadrático medio de aproximación por grados de libertad muestra resultados satisfactorios (RMSEA=.046) y el índice de bondad de ajuste también resulta favorable (GFI=.974).
A pesar de que las medidas de fiabilidad de las puntuaciones obtienen buenos resultados (Ω=.90; α=.91), los análisis de los índices que evalúan la consistencia de los factores refuerzan la sospecha de problemas en el ajuste del modelo previamente reveladas por el RMSR, dado que los cuatro indicadores de calidad y efectividad de las estimaciones para las puntuaciones de los factores mostraron resultados por debajo de los puntos críticos para los factores 3 y 4, por lo que es apropiado atender la recomendación del análisis paralelo (AP) de rotar la matriz para extraer dos (2) factores.
Análisis descriptivo y correlacional de ítems para el modelo de dos factores
Para llegar al modelo definitivo de dos factores se probaron varias soluciones, inicialmente la extracción se hizo con todos los ítems y el análisis condujo a descartar los reactivos 9, 11, 23, 24 y 30 por presentar cargas absolutas inferiores a .30. Procurando una mejor respuesta de los ítems se subió el umbral de las cargas a .40 (Lloret-Segura et al., 2014) lo que también descartó los ítems 12, 14, 16 y 19. Tras una segunda rotación los ítems 3, 8, 17 y 31 dejaron de ofrecer cargas sobre el umbral definido por lo que fueron eliminados, una tercera rotación generó un modelo de 19 ítems en el cual los número 1, 4, 5, 10, 11 y 28 fueron eliminados por su baja carga. El resultado fue una versión de 13 ítems retenidos en dos factores, cuyos datos descriptivos se encuentran en la Tabla 3. El análisis descriptivo multivariado mostró datos significativos (asimetría=56.114, curtosis=296.434, p=.001<.05).
Tabla 3: Datos descriptivos de los 14 ítems finales evaluados
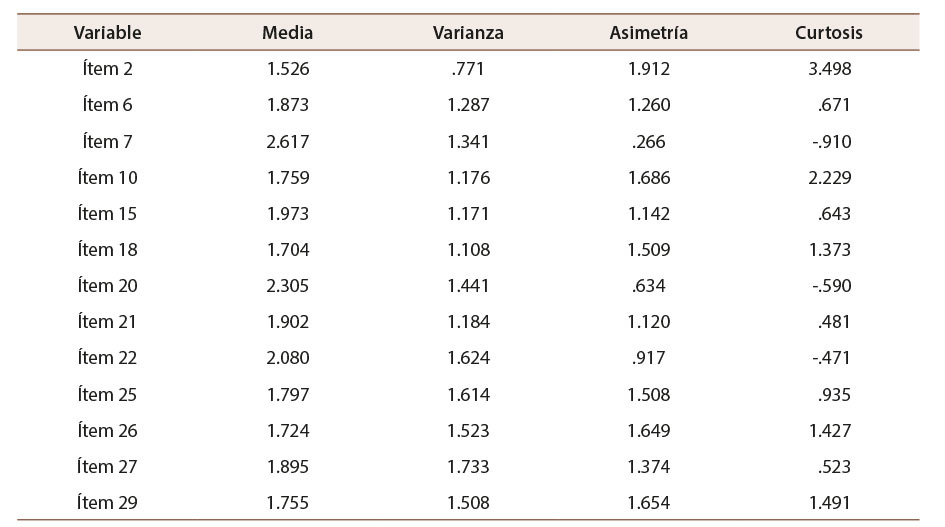
Nota: Elaboración propia.
Los valores de adecuación de la matriz en esta ocasión fueron buenos (Bartlett = 3795.8, p=.001<.05; KMO = .85). En la Tabla 4 se describe la matriz de correlaciones policóricas del modelo.
Por su parte, en la Tabla 5 se incluyen los datos de las matriz no rotada y rotada, identificando en esta última el modelo factorial final, compuesto en su primer factor por 3 ítems que explican 48% de proporción de la varianza, mientras que el segundo factor contiene 10 ítems que explican 12% de la proporción de la varianza, juntos explican 60% del total de la varianza. Además, los fatores muestran correlación con un valor de .581.
Los criterios de bondad de ajuste fueron modestos, en un principio el RMSEA obtuvo un valor de .06 el cual es justo, dado que si bien supera el valor crítico admisible de .05, no supera el umbral de .08. El índice de bondad de ajuste mostró valores apropiados (GFI=.991) mientras que el RMSR obtuvo un valor de .05. El análisis de fiabilidad de las puntuaciones mantuvo sus buenos resultados tanto en el omega de McDonald (Ω=.89) como en el alpha estandarizado (α=.89), así mismo, las medidas de calidad y replicabilidad de ambos factores son mejores en relación con el modelo de cuatro factores y cumplen con los criterios críticos definidos, lo que sugiere que los reactivos miden apropiadamente cada factor. En la Tabla 6 se describe esta información.
Tabla 4: Matriz de correlaciones policóricas para el modelo factorial fijado en dos factores

Nota: Elaboración propia.
Tabla 5: Cargas factoriales de las matrices antes y después de la rotación definiendo solución final de dos factores
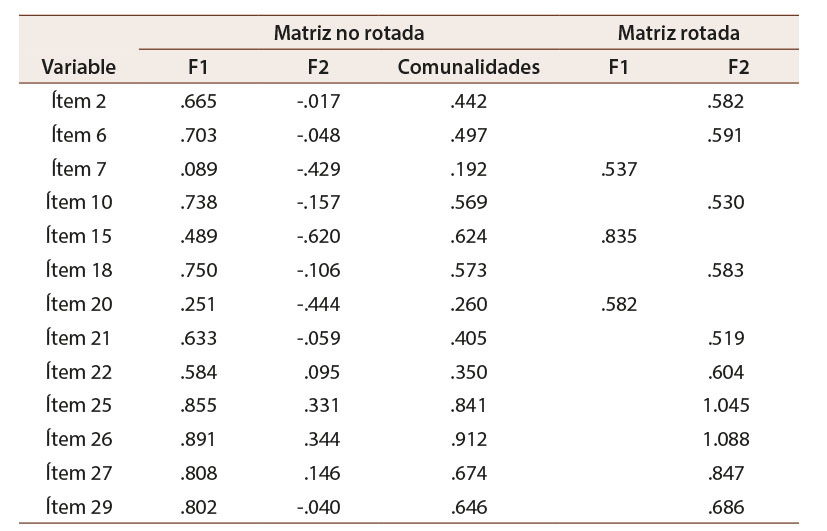
Nota: Elaboración propia.
Tabla 6: Comparación de los indicadores de calidad y efectividad, replicabilidad y confiabilidad calculados para el modelo de dos factores
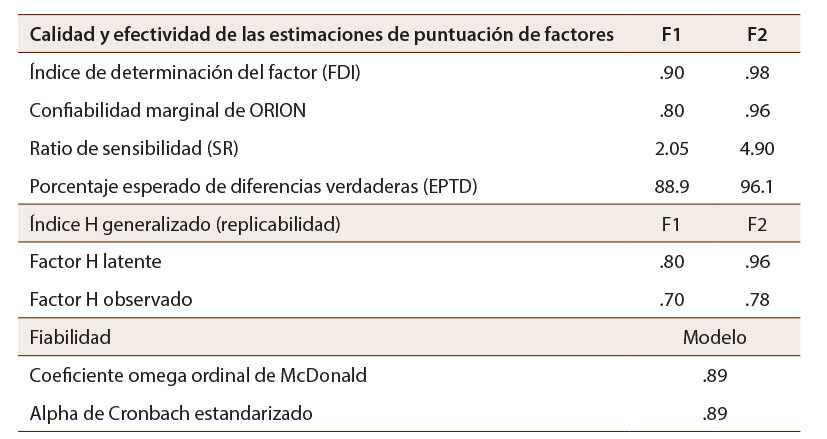
Nota: Elaboración propia.
En resumen, la versión definitiva del instrumento la componen dos factores, el primero se denomina dificultad en el aprendizaje de la matemática y contiene tres ítems (7,15,20) de las dimensiones previas habilidad y ansiedad, todos ellos son de tipo negativo. El segundo factor se denomina beneficio de la matemática e incluye seis ítems de la dimensión previa de aplicabilidad (2,6,10,18,22,26), tres ítems de afectividad (21,25,29) y uno de habilidad (27), de los cuales dos tienen puntuación inversa (21 y 29).
Discusión
Este estudio tuvo por objetivo el análisis de las propiedades psicométricas de la Escala de actitudes hacia la matemática (EAHM-U) en estudiantado universitario de Colombia, aplicando los lineamientos internacionales para el tratamiento de datos dirigido a la validación de escalas. Este proceso se cumplió de forma puntual en una muestra de estudiantes de Licenciatura en Matemáticas.
La evaluación inicial del instrumento en sus propiedades descriptivas y posteriormente a través de análisis factorial exploratorio ha conducido a considerar que la estructura factorial propuesta originalmente en cuatro dimensiones no se ajusta a las condiciones de la población, incluso el procedimiento genera una gran variedad de componentes con pocos ítems cuyas cargas factoriales se ubican debajo del límite considerado en este estudio (.40), valor que supera el convencionalmente pensado en .30 desde la propuesta tradicional de validación de pruebas, por lo cual garantiza que los ítems incluidos realmente responden a valores factoriales importantes y descartan aquellos reactivos con poco aporte que pueden afectar el funcionamiento general de la prueba.
De hecho, la supresión de ítems ayudó a que la solución definitiva fuera mucho más clara, además de redundar en la mejora representada en los indicadores que informan sobre la consistencia y replicabilidad de las puntuaciones. Esto ha conducido a la redefinición de las dimensiones a partir de lo sugerido por el análisis paralelo que condujo a fijar una solución bidimensional. En este proceso se descartaron 18 ítems, lo cual dio como resultado la retención de dos dimensiones constituidas por 13 ítems, el primer factor se ha denominado dificultad en el aprendizaje de la matemática y se compone de ítems que previamente se incluían en las dimensiones de habilidad y ansiedad, mientras que el segundo factor se ha denominado beneficio de la matemática e incluye ítems que previamente respondían a las dimensiones de aplicabilidad, afectividad y habilidad.
Estas dimensiones plantean respuestas actitudinales diametralmente opuestas, dado que tanto su contenido como su aproximación afectiva es diferente. La primera dimensión comporta una connotación afectiva negativa donde se resalta la preocupación e incluso la valoración negativa de destrezas en el área de matemáticas, relacionándose, por ende, con una actitud desfavorable hacia los contenidos tratados, mientras que la segunda dimensión evalúa una aproximación positiva hacia la matemática en educadores y educadoras en formación inicial, la cual responde a las nociones de utilidad de la disciplina e incluye el disfrute (agrado/desagrado) por su estudio.
Esta solución bidimensional coincide con las estructuras ofrecidas por otros instrumentos disponibles, la versión del Math Attitude Scale de Aiken (1974), por ejemplo, es unas de las pruebas clásicas en la materia que diferencia una dimensión enfocada en el valor dado a la matemática y el disfrute hacia esta, así mismo, las dimensiones identificadas en esta adaptación del EAHM-U también guardan relación con la propuesta de Gairín Sallán (1990), quien diferencia el gusto y la utilidad como componentes actitudinales en el tema. Más recientemente Adelson y McCoach (2011) desarrollaron The Math and Me Survey en la cual definen una solución bidimensional que se ajusta a la medición del disfrute y de la autopercepción del estudiantado ante la matemática, algo bastante cercano a la solución identificada en este estudio.
En lo referente a confiabilidad de las puntuaciones ofrecidas por el instrumento, este estudio considera medidas tradicionales basadas en la consistencia interna como el alpha de Cronbach, pero conociendo sus limitaciones y en función del nivel de gradación de la escala se han calculado el omega de McDonald como medida basada en cargas factoriales, lo cual es ampliamente respaldado por la bibliografía (Ventura-León y Caycho-Rodríguez, 2017), así mismo, se han incluido medidas de replicabilidad que robustecen este análisis. Los hallazgos demostraron que el modelo basado en dos dimensiones presenta apropiados datos de fiabilidad en las puntuaciones obtenidas; además, el análisis de replicabilidad demuestra que los reactivos responden de forma apropiada a la dimensión en la cual han sido retenidos.
Finalmente, los estadísticos de bondad de ajuste del modelo factorial, si bien no alcanzan valores excelentes, responden con cierta solvencia a las exigencias mínimas al ubicar un valor RMSEA por debajo .08, así como un índice de bondad GFI muy cercano a 1. Solamente el valor de RMSR se encuentra ligeramente superior al límite crítico, pero el análisis conjunto de los indicadores deja asumir un comportamiento aceptable del modelo.
Es importante reseñar que este estudio se ha enfocado en las recomendaciones técnicas actuales para la revisión de propiedades de pruebas de medición (Lloret-Segura et al., 2014), lo que ha permitido la escogencia de procedimientos estadísticos ajustados a las condiciones del instrumento y a las características de la muestra. El análisis incluye desde el reporte de procesos de imputación (poco habitual en la bibliografía instrumental), hasta la aplicación de modelos robustos para comprobar supuestos que definan apropiados niveles de consistencia en los resultados ofrecidos por el instrumento. De esta forma, al superar “la medida estándar” enfocada en rotaciones ortogonales, uso de la regla Kaiser, revisión de matriz de correlaciones de Pearson (cuando en realidad se tratan datos obtenidos con escala de gradación), este proceso de validación psicométrica supera muchos de los problemas reseñados por la bibliografía especializada al momento de probar la estructura factorial de pruebas psicológicas o cuestionarios de medición (Lloret-Segura et al., 2014).
Se concluye, entonces, que la versión del EAHM-U para estudiantes de educación matemática responde a características psicométricas buenas, que garantizan la medición de las dimensiones propuestas, por lo que puede pasar a ser un instrumento disponible para la investigación enfocada en el análisis del dominio afectivo de la matemática a nivel de futuros educadores y educadoras del área.
Declaración de contribuciones
Las personas autoras declaran que han contribuido en los siguientes roles: J. H. A. T. contribuyó con la escritura del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación. L. J. V. D. contribuyó con la escritura del artículo; la gestión del proceso investigativo; la obtención de fondos, recursos y apoyo tecnológico y el desarrollo de la investigación. M. F. A. M. contribuyó con la escritura del artículo y el desarrollo de la investigación. J. C. D. L. C. G. contribuyó con la escritura del artículo y el desarrollo de la investigación.
Referencias
Adelson, J. L. y McCoach, D. B. (2011). Development and psychometric properties of the math and me surven. Measurement and Evaluation in Counseling and Development, 44(4), 225-247. https://doi.org/10.1177/0748175611418522
Aiken, L. R. (1974). Two scales of attitude toward mathematics. Journal for Research in Mathematics Education, 5(2), 67-71. https://doi.org/10.2307/748616
Aiken, L. R. y Dreger, R. M. (1961). The effect of attitude on performance in mathematics. Journal of Educational Psychology, 52(1), 19-24. https://doi.org/10.1037/h0041309
Alemany Arrebola, I. y Lara, A. I. (2010). Las actitudes hacia las matemáticas en el alumnado de ESO: Un instrumento para su medición. Publicaciones, 40, 49-71. https://digibug.ugr.es/handle/10481/24720
Aparicio, A. S. y Bazán, J. L. (1997). Actitudes hacia las matemáticas en ingresantes a la Universidad Nacional Agraria la Molina. Más Luz. Revista de Psicología y Pedagogía, 3(2), 351-38. https://dokumen.tips/documents/actitudes-hacia-las-matematicas-en-ingresantes-a-jbazandownload-mas-luz.html?page=1
Auzmendi Escribano, E. (1992). Las actitudes hacia la matemática-estadística en las enseñanzas media y universitaria. Características y medición. Mensajero.
Casas-Rosal, J. C., Villarraga Rico, M. E., Maz-Machado, A. y León-Mantero, C. (2018). Factores de influencia en las actitudes hacia la estadística de alumnos de educación media. Revista Espacios, 39(52), 1-12. https://www.revistaespacios.com/a18v39n52/18395233.html
Casis, M., Rico, N. y Castro, E. (2017). Motivación, autoconfianza y ansiedad como descriptores de la actitud hacia las matemáticas de los futuros profesores de educación básica de Chile. PNA, 11(3), 181-203. https://doi.org/10.30827/pna.v11i3.6073
Cerda, G., Ortega Ruiz, R., Casas, J. A., del Rey, R., y Pérez, C. (2016). Predisposición desfavorable hacia el aprendizaje de las matemáticas: Una propuesta para su medición. Estudios pedagógicos (Valdivia), 42(1), 53-63. http://dx.doi.org/10.4067/S0718-07052016000100004
Duarte-Sepúlveda, L. C., Ricardo-Quiñones, N. y Santos-López, L. V. (2018). Dominio afectivo de los estudiantes de educación media hacia las matemáticas. Revista Perspectivas, 3(2), 60-71. https://doi.org/10.22463/25909215.1589
Dutton, W. H. y Perkins Blum, M. (1968). The measurement of attitudes toward arithmetic with a Likert-type test. The Elementary School Journal, 68(5), 259-264. https://doi.org/10.1086/460443
Estrada Roca, A., y Diez-Palomar, J. (2011). Las actitudes hacia las matemáticas. Análisis descriptivo de un estudio de caso exploratorio centrado en la educación matemática de familiares. Revista de Investigación en Educación, 9(2), 116-132. https://reined.webs.uvigo.es/index.php/reined/article/view/118
Fennema, E. y Sherman, J. A. (1976). Fennema-Sherman Mathematics Attitudes Scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for Research in Mathematics Education, 7(5), 324-326. https://doi.org/10.2307/748467
Ferrando, P. J. y Lorenzo-Seva U. (2018). Assessing the quality and appropriateness of factor solutions and factor score estimates in exploratory item factor analysis. Educational and Psychological Measurement, 78(5), 762-780. https://doi.org/10.1177/0013164417719308
Gairín Sallán, J. (1990). Las actitudes en educación. Un estudio sobre la educación matemática. PPU.
Gamboa Araya, R. y Moreira-Mora, T. E. (2017). Actitudes y creencias hacia las matemáticas: Un estudio comparativo entre estudiantes y profesores. Actualidades Investigativas en Educación, 17(1), 1-45. http://dx.doi.org/10.15517/aie.v17i1.27473
Ingram, N., Hatisaru, V., Grootenboer, P. y Beswick, K. (2020). Researching the affective domain in Mathematics Education. En J. Way, C. Attard, J. Anderson, J. Bobis, H. McMaster y K. Cartwright, (Eds.), Research in mathematics education in Australasia 2016-2019 (pp. 147-175). Springer.
Itter, D. y Meyers, N. (2017). Fear, loathing and ambivalence toward learning and teaching mathematics: Preservice teachers’ perspectives. Mathematics Teacher Education and Development, 19(2), 123-141. https://eric.ed.gov/?id=EJ1160848
Lloret-Segura, S., Ferreres-Traver, A., Hernández-Baeza, A. y Tomás-Marco, I. (2014). El análisis factorial exploratorio de los ítems: Una guía práctica, revisada y actualizada. Anales de Psicología, 30(3), 1151-1169. https://dx.doi.org/10.6018/analesps.30.3.199361
Lorenzo-Seva, U. (1999). Promin: A method for oblique factor rotation. Multivariate Behavioral Research, 34(3), 347-365. https://doi.org/10.1207/S15327906MBR3403_3
Lorenzo-Seva, U. y Ferrando, P. J. (2006). FACTOR: A computer program to fit the exploratory factor analysis model. Behavioral Research Methods, Instruments and Computers, 38, 88-91. https://doi.org/10.3758/BF03192753
Mato Vázquez, M. D. y Muñoz Cantero, J. M. (2010). Efectos generales de las variables actitud y ansiedad sobre el rendimiento en matemáticas en alumnos de educación secundaria obligatoria. Implicaciones para la práctica educativa. Ciencias Psicológicas, 4(1), 27-40. https://doi.org/10.22235/cp.v4i1.109
Mejía Saldaña, A., Sánchez Ruiz, J. G. y Juárez López, J. A. (2018). Actitudes hacia las matemáticas en estudiantes universitarios de ingeniería y matemáticas. En C. Dolores Flores, G. Martínez Sierra, M. S. García González, J. A. Juárez López y J. C. Ramírez Cruz (Eds.), Investigaciones en dominio afectivo en matemática educativa (pp. 225-242). Ediciones Eón; UAG.
Michaels, L. A. y Forsyth, R. A. (1977). Construction and validation of an instrument measuring certain attitudes toward mathematics. Educational and Psychological Measurement, 37(4), 1043-1049. https://doi.org/10.1177/001316447703700429
Palacios, A., Arias, V. y Arias, B. (2014). Las actitudes hacia las matemáticas: Construcción y validación de un instrumento para su medida. Revista de Psicodidáctica, 19(1), 67-91. https://doi.org/10.1387/RevPsicodidact.8961
Ramírez Cruz, J. C., Verduzco Montes, M., y García Rosales, A. (2018). Validez y confiabilidad de una escala para medir actitudes hacia las matemáticas en educación especial. En C. Dolores Flores, G. Martínez Sierra, M. S. García González, J. A. Juárez López y J. C. Ramírez Cruz (Eds.), Investigaciones en dominio afectivo en matemática educativa (pp. 243-260). Ediciones Eón; UAG.
Rodríguez Jiménez, O. y Mora Mojija, S. (2016). Análisis psicométrico del instrumento actitudes hacia las matemáticas mediante el modelo de respuesta graduada de Samejima. Actualidades en Psicología, 30(120), 7-30. http://dx.doi.org/10.15517/ap.v30i120.18722
Sandman, R. S. (1980). The Mathematics Attitude Inventory: Instrument and user’s manual. Journal for Research in Mathematics Education, 11(2), 148-149. https://doi.org/10.2307/748906
Tapia, M. y Marsh, G. E. (2004). An instrument to measure mathematics attitudes. Academic Exchange Quarterly, 8(2), 16-21.
Tran, D. y Javed, S. (2017). Examining non-traditional pathway preservice teachers’ attitudes towards mathematics. En A. Downton, S. Livy y J. Hall (Eds.), 40 yearson: We are still learning! Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia (pp. 506-513). MERGA.
Ursini, S., Sánchez, G. y Orendain, M. (2004). Validación y confiabilidad de una escala de actitudes hacia las matemáticas y hacia las matemáticas enseñadas con computadora. Educación matemática, 16(3), 59-78. https://www.revista-educacion-matematica.org.mx/revista/vol16-3-en/
Ventura-León, J. L. y Caycho-Rodríguez, T. (2017). El coeficiente omega: Un método alternativo para la estimación de la confiabilidad. Revista Latinoamericana de Ciencias Sociales, Niñez y Juventud, 15(1), 625-627. https://www.redalyc.org/articulo.oa?id=77349627039
Verdugo, M., Asún, R. y Martínez, S. (2017). Validación de la escala de creencias de eficacia en la enseñanza de la matemática (ECEEM) y caracterización de las creencias de estudiantes de pedagogía básica. Calidad en la Educación, (47), 145-178. https://doi.org/10.4067/S0718-45652017000200145

Artículo de la Revista Electrónica Educare de la Universidad Nacional, Costa Rica by Universidad Nacional is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Costa Rica License.
Based on a work at https://www.revistas.una.ac.cr/index.php/EDUCARE
Permissions beyond the scope of this license may be available at educare@una.ac.cr
