Educare Electronic Journal (Revista Electrónica Educare) EISSN: 1409-4258 Vol. 20(1) JANUARY-APRIL, 2016: 1-22

doi: http://dx.doi.org/10.15359/ree.20-2.13

URL: http://www.una.ac.cr/educare

EMAIL: educare@una.cr

[Published on January 1st, 2016]

 

---

The Application of a Digital Educational Resource to the Learning Difficulty of Subtraction: A Case Study

La aplicación de un recurso educativo digital en la dificultad de aprendizaje de la resta: Un estudio de caso

Immaculada Margalef-Ciurana1

Escola Misericòrdia

Reus, Spain

imargalefc@uoc.edu

Consuelo García-Tamarit2

Universitat Oberta de Catalunya

Barcelona, Spain

cgarciat@uoc.edu

Received March 1, 2015 • Revised November 1, 2015 • Approved November 17, 2015

Abstract. The lack of an adequate and organized transfer of steps in the subtraction process results in a learning difficulty of this operation in elementary school. The objective of this study is to show how the use of a digital educational resource can help improve the mathematical performance of children with dyscalculia. In particular, how the systematic application of a digital resource improves the resolution of subtraction, compared to the resolution of such operation without it. The study was carried out by applying a learning sequence of systematized subtraction and adapting it to the specific difficulties of the student and then selecting a motivating digital resource. Our results suggest that the use of this resource has made outstanding contributions to the achievement of this mathematical operation. It is recommended to carry out studies in this line to contribute to improving the learning process of school children with these difficulties.

Keywords. Subtraction learning, learning disability, mathematical difficulty, digital educational resource.

Resumen. La falta de una transferencia secuenciada y adecuada de los pasos del proceso de la resta es origen de una dificultad en el aprendizaje de esta operación en primaria. El objetivo de esta investigación es mostrar cómo la utilización de un recurso educativo digital puede ayudar a mejorar el rendimiento matemático de niños y niñas con discalculia. En concreto, cómo la aplicación sistemática de un recurso digital mejora la resolución de la resta, comparándolo con la resolución de dicha operación sin él. El estudio se realizó aplicando una secuencia de aprendizaje de la resta sistematizada y adaptada a las dificultades específicas de la estudiante y seleccionando un recurso digital motivador. Nuestros resultados sugieren que la utilización del recurso ha contribuido de manera destacada al logro de esta operación matemática. Se recomienda realizar estudios en esta línea para contribuir a la mejora del aprendizaje de escolares que presentan estas dificultades.

Palabras claves. Aprendizaje de la resta, dificultades de aprendizaje, dificultades matemáticas, recurso educativo digital.

Difficulties in learning to subtract

The concept of learning difficulties in curricular content can be defined as “a problematic educational situation originated by the existing excessive distance between demand in a learning task and the competency of a student or group of students to solve the task” (Badia, 2012, p. 18). This concept highlights that the level of initial competency of the student is below the level required to complete the task. That’s why, when planning for interventions in students who have learning difficulties, it is necessary to know their personal characteristics, but also to analyze their difficulties taking into account the teaching and evaluation processes carried out by specialists in education.

The difficulties students face in mathematical contents and processes can be interpreted from the point of view of cognitive schemata as being inappropriate to solve the tasks at hand (Badia, 2012). One of the difficulties is related to numerical sense, the way of reasoning with and about numbers. The objective of this case study is to show how the application of a digital educational resource adapted to the needs of a student helps her to overcome a learning difficulty related to subtraction by emphasizing the reinforcement of a sequenced and appropriate transference of the steps in the subtraction process.

Not all learning difficulties in primary school mathematics are a result of intellectual impairment or inappropriate schooling. Between 5% and 8% of students report some cognitive deficit or type of memory that interferes with their ability to learn concepts from mathematics (Geary, 2004). This difficulty is characterized by problems in assimilating and remembering numerical and arithmetical data (Geary & Hoard, 2001; Rossellia & Matute, 2005; Shalev & Gross-Tsur, 2001), performing calculations, and generating strategies for the resolution of the problems provided (Landerl, Bevan & Butterworth, 2004).

In order to improve the teaching of mathematics, textbooks suggest reflecting to promote abstractions and suggestive deductive processes, and developing applications that allow the content to be inserted in the real world (Giménez, 1999) and not just engage in repetition of specific concepts. The learning of mathematics is not achieved by the application of repeated movements, but by the amount of ideas that are related in the process (Fernández, 2005). So, in order to introduce improvements to the learning process of math, it is necessary to focus on the learning process itself (Marcelo, 2001), and make the knowledge achieved part of one’s own reflection that stems from one’s previous knowledge (Cebrián, 1999).

Several studies have focused on elementary subtraction. Firstly, Robinson (2001) determined the relationship between the development of subtraction abilities and the improvement of the global arithmetic knowledge of the students, measuring the mathematical knowledge of procedures, facts, and concepts. It concluded that it is necessary to take into account the student’s individual differences in conceptual knowledge when developing arithmetic skills. Siegler (1987), on the other hand, showed the importance of compiling verbal records that offer relevant information on how children solve arithmetical problems. According to the model by Siegler and Jenkins (1989) for the development of subtraction strategy, when solving a subtraction, the choice of strategy depends on two parameters: the strength of the associations between the operation to be performed (for example, 6-2) and the possible answers (1, 2, 3) and, second, the trust criteria that measures the confidence of the student about the accuracy of the answer given.

Secondly, concerning the study of errors in the subtraction algorithm, we found the theory of VanLehn, which incorporates a thorough analysis of the procedural mechanisms that govern the generation of systematic errors (Brown & Burton, 1978; Brown & VanLehn 1980; Brown & VanLehn, 1982; López & Sánchez, 2006; VanLehn, 1982, 1983, 1987, 1990; Young & O´Shea, 1981. For these writers, the problem lies in the failure of the execution process for the subtraction algorithm. These researchers show the nature and representation of the different patterns of error. Errors are incurred in when students incorrectly memorize the steps in the process, be it omissions, intrusions, or permutations. In this way, it is possible to find students that, when doing subtractions, omit one of the steps, mix the components, permute the order of the steps, o include steps from other processes, for example, addition.

On the other hand, other researchers (Fuson, 1986, 1992a; 1992b; Fuson & Briars, 1990; Hiebert & Lefevre, 1986; Hiebert & Wearne, 1996; Ohlsson & Rees, 1991; Resnick, 1982, 1983; Resnick & Omanson, 1987) point out the relevance of acquiring the conceptual components that govern algorithmic procedures. These components refer to the comprehension of the principles related to the acquisition of the decimal system, the capacity to count, the acquisition of the numerical sequence, the manifestation of the key concepts related to numbers, as well as the comprehension of the arithmetic functioning of the algorithm of subtraction.

Lastly, there are some authors (Fiori & Zuccheri, 2005) who consider that the errors in the subtraction calculations are a natural stage and cannot be avoided in the process of knowledge acquisition.

The interaction among the contextual, intuitive, and formal components influences the learning process of children who experience those difficulties. This type of student does not have enough conceptual resources to successfully solve subtractions and, when faced with new situations, is not sure how to operate. According to Hiebert and Lindquist (1990), when doubt arises, these students use the analogy but do not produce a correct sequenced transference of the steps. They transfer isolated steps, but not the whole process. That is why, in the context of the classroom, it is necessary to take into account the interpretations and resources used by the children when solving subtractions; they significantly influence the conceptual knowledge and the relationship that the child has to establish with this type of knowledge (Sánchez & López, 2009).

Errors in subtraction can be classified in different categories according to their origin. One classification (Sierra model, as cited in Van Lehn, 1990, p. 202) proposes a distinction between errors or bugs systemically made by the students throughout different courses: always-borrow-left, blank-instead-of-borrow, borrow-across-second-zero, borrow-across-zero, borrow-don’t-decrement-unless-bottom-smaller, borrow-from-one-is-nine, borrow-from-one-is-ten, borrow-from-zero, borrow-from-zero-is-ten, borrow-no-decrement, borrow-no-decrement-except-last, borrow-treat-one-as-zero, doesn’t borrow-except-last, don’t-decrement-zero, forget-borrow-over-blacks, N-N-causes-borrow, only-do-units, quit-when-bottom-blank, smaller-from-larger, smaller-from-larger-except-last, smaller-from -larger-instead-of-borrow-from-zero, smaller-from-larger-instead-of-borrow-unless bottom, stops-borrow-at-multiple-zero, stops-borrow-at-zero, top-instead-of-borrow-from-zero3.

Another classification (Cid, Godino & Batanero, 2003) distinguishes between the following errors: (1) in the positioning of numbers, (2) in the order of obtaining basic numerical tasks, (3) in obtaining basic numerical facts, (4) in subtraction of smaller from larger, (5) in positioning a zero, (6) in empty places, and (7) in carrying and writing the complete result.

A third classification (López & Sánchez, 2007) distinguishes between the influence of subtraction’s conceptual structure and its relation to zero. For example, when borrowing from zero, this changes to nine, but there is no longer any gaining from the column to the left.

Lastly, there is the proposal from Noda and Bruno (2009) on the classification of errors based on the analysis of the subtraction process and its algorithm (table 1).

The application of digital educational resources for the learning of subtraction

The integration of technology in education offers many possibilities at different levels (didactic, informative, social). Besides the pedagogical value of the resource, there is the motivation factor and the thrill it provokes in students. Using different technological tools allows for a change in the teaching-learning process and for the improvement of motivation and socialization in the classroom (Aguaded & Muñoz, 2012). Additionally, the use of digital resources for the learning of mathematics enriches the process by allowing students to develop their communicative competency and foster their motivation and interest in the topic, while paying more attention and concentration in class (González, 2012).

Nevertheless, introducing technology to education in general, and to the learning of subtraction in particular, does not imply a significant change in the results or in the teaching practice despite its contribution for motivating students. In this sense, authors such as Burton & Brown (1982), Carbonell (1970), López and Sánchez (2009) and Martin and VanLehn (1995) have researched the use of computers as a complement in dealing with arithmetic errors. These researchers have shown the influence of hypermedia in formal and procedural knowledge in the learning process of the subtraction algorithm; they have concluded that instruction supported by a methodology that makes use of digital resources influences the conceptual command to learn subtraction. (López & Sánchez, 2009).

In this sense, the use of technology can help use target all rhythms and learning styles while offering educators the possibility of making use of different formats and support to work content areas. Following the description that Jonassen (1997) gives of problems, a student with learning difficulties in subtraction must solve well-structured and situated problems, with a level of complexity adapted to their motivation and previous knowledge. In this way, technology could be efficiently used to promote significant learning among students.

Peltenburg, van den Heuvel-Panhuizen and Robitzsch (2010) researched the mathematical potential of students with special needs specifically regarding subtraction up to 100. They developed and used an evaluation instrument for a standardized written test in digital media. The grades of the students who took the digital version were compared to the items in the written test. The results showed that the dynamic evaluation based on technology could help the students develop their potential in doing subtraction.

Waiganjo and Wausi (2013) pointed out that the use of technology could improve the mathematical performance of students with learning difficulties in the area, specifically of those who suffered from dyscalculia. They also pointed out the need to take into account the teacher’s attitude, their previous experience, as well as the software and hardware used in order for the digital resources to be effective in helping students overcome their difficulties.

In this study, we work with the hypothesis that the use of a digital educational resource that focuses on subtraction will contribute to improve the performance of the student in this operation.

Methodology

The qualitative research is framed by a critical constructivist paradigm. On one hand, it focuses on describing and interpreting educational phenomena and is interested in the discovery of guidelines and patterns to understand the meaning and construction of personal knowledge. On the other hand, it is a critical study since the research presupposes that the systematic use of a digital educational resource could improve a specific learning difficulty.

Participant

When defining the selection criteria for participating in the study, we looked for students who were diagnosed by a team of educational psychologists with having learning difficulties in mathematics, specifically in subtraction; students were also part of the public education system and had authorization from parents. In this case, the student chosen was a girl who at the moment of the study was 10 years and 3 months old. Her family circle was stable and was classified as belonging to a low socioeconomic status. She had been a student in the special education class of a public school since the age of 4. Her diagnosis showed she had learning difficulties in mathematics (specifically in subtraction) and language. Her case was overseen by the team of pedagogical psychologists.

Instruments

The decision was made for a case study, one of the modalities used in constructivism for the compilation of data. The information was compiled using interviews (tutor, specialist in special education, family), direct observation, and registry of the test results of subtractions performed both, digitally and in paper. Data triangulation was used for the analysis of the information collected during the sessions.

During the initial evaluation, data was collected using:

• Psyco-technical tests.
• Semi structured interview with the tutor and specialist in special education.
• Semi structured interview of the family.
• Initial written evaluation test on subtraction.

Several searches were performed, in order to choose the digital resource, which had to contribute to the student’s success in subtraction. The digital educational resource had to meet the following requirements: vertical subtraction, one and two-digit subtraction, and subtraction with and without borrowing; since that was the type of subtraction that the student regularly performed in class and in order to compare the evolution in the process.

The resource chosen is called “Ejercicios de restar” (Dibujos para pintar, 2004-2014). It does subtraction vertically, it allows the user to choose the number of digits and whether borrowing is allowed or not. Whenever the subtraction is done incorrectly, it is possible to correct it or move on to the next exercise. It is also possible to print the results to measure the evolution and the errors. It gives the user 5 minutes to solve a subtraction problem.

After using the digital resource, the following instruments were used for the final assessment:

• Result of subtractions done using the digital resource.
• A summary chart of the student’s evolution doing subtraction online.
• Final written subtraction test.

Preliminary assessment

The student tool several tests; these are their results:

WISC-IV: low scores below her chronological age in verbal comprehension, perceptive reasoning, memorization of letters and numbers, speed of processing and resolution.

TALEC for reading and writing: reading was very slow but fluid; she divided into syllables and spelled, made errors of omission and substitution. In reading comprehension she achieved level 1, in spelling she achieved level 2 for natural gammar and level 1 for random spelling and speed.

The student’s attitude in the classroom was good, as well as her disposition and effort, which did not correspond to her academic results. She could perform addition but not subtraction. She had many difficulties in the resolutions of problems and serialization. In her relationships with classmates the student was shy; she was accepted by others despite her lack of ongoing contact with them.

At the school, she participated in the special education classroom two hours a week where she would work on Reading and Reading comprehension. In the rest of the classes, the work was adapted to her needs taking into account the curricular adaptation made for her. In the classroom, ICTs were rarely used; the tutor only used them to supplement her explanations.

At home, the student’s behavior and her relationship with her brother and parents were good. The parents were not aware of her limitations and said that if the student did not make an effort, it was due to lack of interest. The mother was the one who offered help when the student asked for it. She would mostly do homework by herself.

Initial assessment

The student did a written exercise of 10 regular subtractions and 10 subtractions by regrouping (figure 1).

The tutor carried out the initial assessment for 17 minutes. The student had to do 20 subtractions. During the session, the student did not ask for help at any time; she seemed to be concentrating on solving the subtractions. The student took the test in a classroom by herself, with no other students or distractors.

The student correctly solved 70% of the simple subtractions and 30% of the subtractions with borrowing out of 20 subtractions, 10 simple (5 of 1 digit and 5 of 2 digits) and 10 borrowing (all of 2 digits).

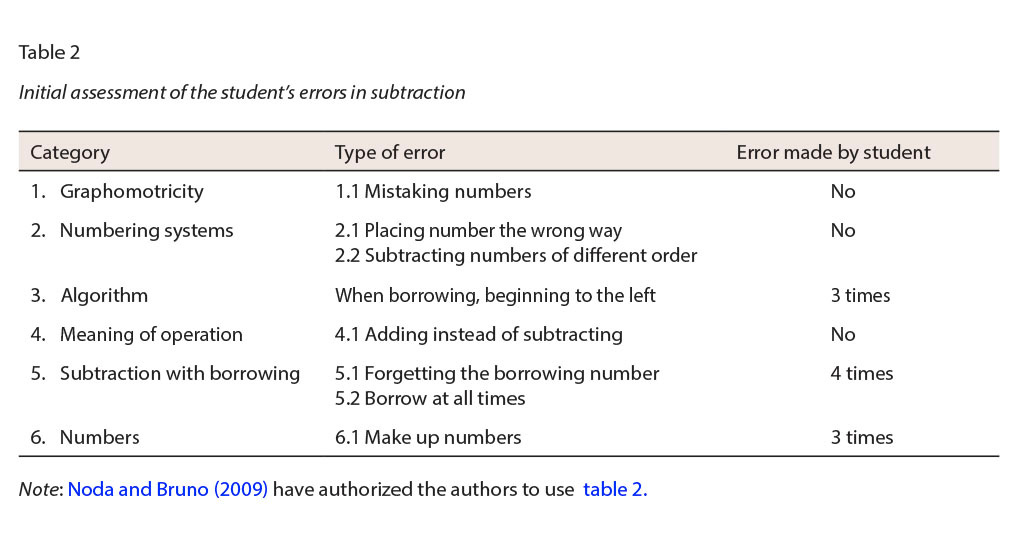
We use the categories by Noda and Bruno (2009) to assess her difficulties in solving subtractions:

First, we observed that the student did not have problems with graphomotricity, numbering system, or meaning of the operation.

Nonetheless, she made mistakes in the algorithm: 3 times she began from the left. She also made mistakes in borrowing subtraction; 4 times she forgot about the borrowing, and 3 times she made up the numbers (table 2).

Learning with digital resource

Once the errors were identified, the student used the digital resource to solve subtractions during 4 weeks, 4 times a week.

There were a total of 16 sessions that complemented the work the student did in the classroom taking into account the content adaptations defined for her. These 16 sessions lasted approximately 15 minutes, and took place in a classroom with laptop and internet access. She worked individually; we made sure distractors from other classrooms where minimal.

The first five sessions were devoted to 1-digit subtraction. The remaining 11 sessions were devoted to 2-digit subtraction: 5 to simple subtraction and 6 to 2-digit subtractions with borrowing.

At the beginning of each session, the student moved from her classroom to the computer room with her special education teacher. Before beginning the session, for 5 minutes the student relaxed by doing breathing exercises and other relaxation exercises with her teacher in order to relieve tension and be able to focus on the mathematical problems.

During 5 minutes, she would do the subtraction exercises using the digital tool. She could choose the type of subtractions to solve according to the instructions given by her special education teacher. When presented with an exercise, the student first observed the minuend and subtrahend, as well as the blank spaces used to type the corresponding numbers.

Secondly, she would verbalize each step she needed to follow in order to solve the subtraction. For example, 20-13 is one of the subtractions she was faced with; the vertical subtraction is shown in a central position on the screen for the student to see what she has to do: unit and ten as well as the borrowed ones. To the right of the subtraction, there is a clock to show the time devoted to the operation; there is a clock and the image of a teacher reading on a chair. The verbalization of the aforementioned example was: “I begin to the right, because I cannot subtract 0-3 given that 0 is smaller than 3, the number 2 gives one to the 0 and so now I have 10. Now I can do the subtraction: 10-3 is 7. Now, because the 2 gave one, I have to take it and so I have 1 and 1 minus 1 is 0. Let’s see if I am right… (the student checked the operation). Yes, it’s correct! Now, to the next one”.

Whenever she failed, the tool let her correct the answer or move to the next one. She always tried to correct the answer, but moved on after a couple of unsuccessful attempts. Lastly, she also had the chance to print the results at the end of the session to check her progress and errors.

When she finished subtracting using the tool, the student again engaged in relaxation exercises in order to go back to the classroom and continue with her mathematics lesson. During the session in the classroom, the student had to solve problems similar to the ones she did in the computer, but this time in writing, also during 5 minutes. This allowed her to practice subtraction and check her improvement using the tool. The tutor was in charge of letting the student know whether the answers were correct or not; if not, she could correct them.

Final assessment

At the end of each session, the results were registered on a table to observe her evolution.

At the end of the 16 sessions, the same initial test was given to the student in order to analyze her progress in the algorithm of subtraction. The tutor proctored the test and it was taken in a classroom without any distractors.

Results

Training process

The percentage of subtractions solved correctly the first time, that is, the ones that she did not need to correct, for 1-digit operation, 2-digit operations, and 2-digit borrowing performed using the digital tool in the regular classroom are shown in figure 2.

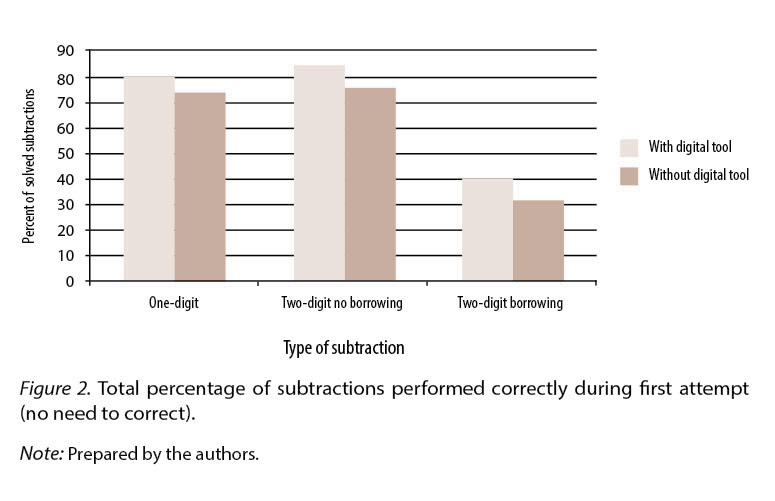
Considering them globally, the number of subtractions the student solved correctly is higher when she used the digital resource than when she didn’t.

a) One-digit subtraction

During each of the first 5 sessions using the digital resource, the student solved between 17 and 24 subtractions (18 in the first session; 17 in the second; 20 in the third; 24 in the fourth and 20 in the fifth) and she had to correct between 3 and 5 (4 in the first; 5 in the second; 3 in the third; 3 in the fourth and 4 in the fifth). The number of subtractions not solved changed between 0 and 2 (1 in the first; 2 in the second; 1 in the third; 1 in the fourth and none in the fifth).

In each of the first 5 sessions without the digital resource, the student correctly solved between 20 and 26 subtractions (19 in the first session; 20 in the second; 22 in the third; 26 in the fourth and 26 in the fifth session) and she had to correct between 5 and 8 (8 in the first; 8 in the second; 5 in the third; 6 in the fourth and 7 in the fifth session). The number of unsolved subtractions ranged between 1 and 3 (2 in the first; 2 in the second; 3 in the third; 2 in the fourth and 1 in the fifth session).

When she used the digital tool, the student solved more subtractions correctly, specifically 80.49% of the subtractions presented the first time, and the percentage of subtractions she had to correct was 15.45%.

When she did not use the digital educational resource, the student correctly solved 71.97% of the subtractions presented the first time and she had to correct 21.66%. Regarding unsolved subtractions, when she used the digital tool, the percentage was 4.06%, while without the use of the tool it was 6.37%.

b) Two-digit subtraction with no borrowing

In each of the 5 sessions devoted to the digital tool, the student solved between 15 and 21 subtractions (15 in the first session; 16 in the second; 19 in the third; 21 in the fourth and 19 in the fifth) and she had to correct between 2 and 3 (3 in the first; 3 in the second; 3 in the third; 2 in the fourth and 3 in the fifth session). The number of subtractions not solved ranged between 0 and 1 (1 in the first; 1 in the second and none in the third, fourth and fifth session).

In each of the 5 sessions when the student did not use the digital resource, the student correctly solved between 17 and 25 subtractions (17 in the first; 19 in the second; 25 in the third; 25 in the fourth and 21 in the fifth session) and she had to correct between 5 and 6 (5 in the first; 5 in the second; 6 in the third; 5 in the fourth and 5 in the fifth session). The number of unsolved subtractions ranged between 0 and 3 (3 in the first; 2 in the second; 0 in the third; 1 in the fourth and 2 in the fifth session).

We noted that with the use of the digital resource, the student solved more subtractions correctly, specifically 84.91% of 2-digit subtractions, and the percentage of operations she had to correct was 13.20%. When she did not use the digital resource, the student correctly solved 75.89% of the subtractions first introduced and she had to correct 18.44%. Regarding unsolved subtractions, with the use of the digital tool the percentage was 1.89% while without the use of the digital tool it was 5.67%.

c) Two-digit subtractions with borrowing

In each of the 6 sessions with the digital resource devoted to subtraction with borrowing, the student solved between 4 and 8 subtractions (5 in the first; 4 in the second; 6 in the third; 5 in the fourth, 8 in the fifth and 6 in the sixth session) and she had to correct between 7 and 9 (7 in the first, second, third, fifth, and sixth sessions; 9 in the fourth). The number of unsolved subtractions ranged between 1 and 2 (1 in the first, fourth, and sixth sessions and 2 in the second, third, and fifth).

In each of the 6 sessions without the digital resource devoted to subtraction with borrowing, the student correctly solved between 3 and 8 subtractions (3 in the first; 4 in the second; 5 in the third; 6 in the fourth, 6 in the fifth and

8 in the sixth session) and she had to correct between 8 and 12 (12 in the first; 11 in the second; 10 in the third; 11 in the fourth and fifth and 8 in the sixth session). The number of unsolved subtractions ranged between 1 and 3 (3 in the first, second, and fourth sessions; 2 in the third and 1 in the fifth and sixth sessions).

When she used the digital resource, the student solved more subtractions correctly, specifically, 39.08% of the 2-digit subtractions with borrowing, and the percentage she had to correct was 50,57%. Without the use of the digital resource, she correctly solved 29.63% of subtractions, and she had to correct 58.33%. Regarding unsolved subtractions, with the use of the digital tool, the percentage was 10.35%, while without the digital resource it was 12.04%.

Final assessment

For the final assessment we used the same test used during the initial assessment. It has a total of 20 subtractions: 10 simple (5 of 1 digit and 5 of 2 digits) and 10 borrowing (all 2-digit subtractions).

The test took 9 minutes and the student correctly solved 90% of the subtractions without borrowing and 40% of the ones with borrowing.

According to the categories defined by Noda and Bruno (2009), the student only made mistakes in subtraction with borrowing on 6 occasions, and when once when she made up a number. She did not make any mistakes in the rest of the categories analyzed (table 3).

Discussion and conclusions

This case study confirms the initial proposal that the use of a digital educational resource can contribute to improve the learning of subtraction in a student diagnosed with learning difficulties in the area. Using the digital tool, the number of subtractions of one and two digits, and two digits with borrowing that were correctly solved during the first attempt increased, as did the number of subtractions corrected by the student with the use of the digital resource, compared to the subtractions done without the resource.

We believe that the positive influence of the digital resource is accounted for by a combination of several factors: the characteristics of the chosen resource, the motivation for using the tool, and the context where the intervention took place.

Firstly, the digital educational resource allowed the student to choose the operations to be solved, go back to correct errors, and print the results in order to visualize the process. The characteristics of the tool chosen made it easier for the student to identify her error, as suggested by authors such as Marcelo (2001) and Cebrián (1999), who mentioned the importance of reflection on the learning of mathematics. The conceptual components governing algorithms were made explicit in this resource, a key element for learning, according to several authors (Fuson & Briars, 1990; Hiebert & Lefevre, 1986; Hiebert & Wearne, 1996; Ohlsson & Rees, 1991; Resnick, 1982; 1983; Resnick & Omanson, 1987).

Another important element was that the student did relaxation exercises to increase her attention and ability to focus. Besides, being able to choose the subtractions gave her a sense of control in the process. The verbalization of the process and the possibility of making corrections allowed the student to be aware of the process involved. Lastly, printing the exercises done, and doing other similar exercising in paper, allowed her to transfer the process from the digital format to the traditional written format.

Likewise, the complexity of the digital resource was adapted to the student’s motivation and previous knowledge (Jonassen, 1997; Robinson, 2001). In this sense, it is important to highlight the need for the tool to categorize the errors in detail so the student can follow the resolution appropriately. In our case, the application of error classification by Noda and Bruno (2009) to initial tests allowed us to become aware of the most frequent errors of the student, and, later, when improvements were seen as a result of the procedure used. Also, this detailed knowledge of the errors in the process allowed us to choose the tool that best matched her previous knowledge.

Secondly, as argued by Aguaded and Muñoz (2012) and González (2012), computers play a motivating role in learning. In the case of our student, the computer was not regularly used in the classroom or at home, so it became an attractive element for doing activity.

Thirdly, an element that has had a positive impact in her improvement was the change in methodology. In this case, we provided individualized attention in each session when the digital tool was used. The student was accompanied by the special education teacher at all times: while she did the relaxation exercises, while she interacted with the digital tool, and during the relaxation exercises at the end of the session, before she returned to the regular classroom. In this way, the student felt she was the protagonist of her own learning process, which probably increased her confidence, a key element for improvement according to Siegler (1987).

This case study has shown us that a student with learning difficulties in subtraction can improve her understanding using a digital tool that supports her previous knowledge, as opposed to no digital tool at all. It has also shown that the training process using a digital resource with those characteristics improves the sequential transference of the steps necessary to learn subtraction.

The results allow us to point out the positive influence of the use of digital educational resources in helping children with learning difficulties in mathematics when those resources are chosen taking into account the student’s needs and previous knowledge, and when the tool is used in the context of an educational setting adapted to those needs.

Nevertheless, some limitation to this study must be considered.

A specific case study does not render useful to generalizing the result despite being representative of learning difficulties in subtraction. It is necessary to apply the resource and the procedure to a bigger sample of students diagnosed with the same difficulties in similar contexts.

In this case, the digital educational resource was used during 16 sessions along 3 weeks. The first 10 sessions were devoted to simple subtraction and, taking into account the results, we concluded that the amount of time devoted was enough. Sixteen sessions were devoted to subtraction with borrowing and, even though the results were positive, we think it was not enough time to get the mechanics of the process and contribute to the success in this operation. It would be advisable to apply the same sequence during a longer period of time while also following the process of using the digital resource and classroom work, as was done with simple subtractions.

We consider it would be important to continue with this line of research, analyzing how and why digital resources can contribute to the improvement of children who have these difficulties. We also advise to use different methodologies that respect the different rhythms and learning styles of students with special characteristics. Lastly, it would be advisable to carry out this type of studies in other areas where students have difficulties with the content so they can succeed in their learning process.

References

Aguaded, J. I., & Muñoz, M. (2012). La competencia digital en el alumnado con necesidades especiales. Uso de ordenadores, tabletas, internet, e-books and narraciones digitales en el aula [Digital competency in students with special needs. Computers, tablets, internet, e-books, and digital storytelling in the classroom] (pp. 1254-1261). In I Congreso Virtual Internacional sobre Innovación Pedagógica and Praxis Educativa INNOVAGOGIA 2012. Sevilla. Retrieved from http://rabida.uhu.es/dspace/ bitstream/handle/10272/7505/La_competencia_digital_alumnado.pdf?sequence=2

Badia, A. (2012). Les dificultats en l’aprenentatge escolar dels continguts curriculars [Learning difficulties in curricular contents]. In A. Badia (Ed.), Dificultats d’aprenentatge dels continguts curriculars [Learning difficulties in curricular contents] (pp. 13-23). Barcelona: FUOC.

Brown, J. S., & Burton, R. R. (April, 1978). Diagnostic models for procedural bugs in basic mathematical skills [Modelos de diagnóstico de errores de procedimiento en las habilidades matemáticas básicas]. Cognitive Science, 2(2), 155-192. doi: 10.1207/s15516709cog0202_4

Brown, J. S., & VanLehn, K. (1980). Repair theory: A generative theory of bugs in procedural skills [Teoría de la reparación: Una teoría generativa de errores en las habilidades de procedimiento]. Cognitive Science, 4, 379-426. Retrieved from http://www.public.asu. edu/~kvanlehn/Stringent/PDF/80CS_JSB_KVL.pdf

Brown, J. S., & VanLehn, K. (1982). Towards a generative theory of “Bugs” [Hacia una teoría generativa de “errores”]. In T. P. Carpenter, J. M. Moser and T. Romberg (Eds.), Addition and subtraction: A cognitive perspective [Suma and resta: Una perspectiva cognitiva] (pp. 117-135). Hillsdale: Erlbaum.

Burton, R. R., & Brown, J. S. (1982). An investigation of computer coaching for informal learning activities [Una investigación sobre coaching informático en actividades de aprendizaje informal]. In D. Sleeman and J. S. Brown (Eds.), Intelligent tutoring systems [Systems of intelligent tutorization] (pp. 79-98). New York: Academic Press.

Carbonell, J. R. (1970). AI in CAI: An artificial-intelligence approach to computer-assisted instruction [IA en EAO: Un enfoque de inteligencia artificial para la enseñanza asistida por ordenador]. Man-Machine Systems, IEEE Transactions on, 11(4), 190-202. doi: 10.1109/ TMMS.1970.299942

Cid, E., Godino, J. D., & Batanero, C. (2003). Sistemas numéricos y su didáctica para maestros [Numbering systems and their didactic process for teachers]. Universidad de Granada. Retrieved from http://www.ugr.es/~jgodino/edumat-maestros/ manual/2_Sistemas_numericos.pdf

Cebrián, M. (1999). La comunicación audiovisual y la informática en los planes de estudios de primaria y secundaria [Audiovisual communication and information technology in the study plans of primary and secondary schools]. In J. Cabero (Ed.), Tecnología educativa [Educational Technology] (pp. 151-161). Madrid: Síntesis.

Dibujos para pintar. (2004-2014). Ejercicios de restar [Subtraction exercises]. Retrieved from http://www.dibujosparapintar.com/juegos_ed_matematicas_restas.html

Fernández, J. A. (2005). Enséñame a contar. Investigación didáctica sobre la técnica de contar como actividad matemática [Teach me to count. Didactic research on the counting technique as a mathematical activity]. Madrid: Grupo Mayéutica.

Fiori, C., & Zuccheri, L. (November, 2005). An experimental research on error patterns in written subtraction [Una investigación experimental sobre los patrones de error en la resta escrita]Educational Studies in Mathematics, 60(3), 323-331. doi: 10.1007/s10649-005-7530-6

Fuson, K. (1986). Role of representation and verbalization in the teaching of multi-digit additions and subtractions [El papel de la representación y la verbalización en la enseñanza de las sumas y restas de varios dígitos]. European Journal of Psychology of Education, 1(2), 35-56. doi: 10.1007/BF03172568

Fuson, K. (1992a). Research on learning and teaching addition and subtraction of whole numbers [La investigación sobre el aprendizaje and la enseñanza de la suma y la resta de números enteros]. In G. Leinhardt, R. Putnam and R. A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching [Análisis de la aritmética para la enseñanza de matemáticas] (pp. 53-187). Hillsdale: Erlbaum.

Fuson, K. (1992b). Research on whole number addition and subtraction [Investigación sobre sumas y restas de números enteros]. In D. A. Grouws (Ed.) Handbook of research on mathematics teaching and learning: a project of the National Council of Teachers of Mathematics [Manual de investigación sobre la enseñanza de las matemáticas y el aprendizaje: Un proyecto del Consejo Nacional de Profesores de Matemáticas] (pp. 243-275). New York: Maxwell Macmillan International.

Fuson, K., & Briars, D. J. (1990). Using base-ten blocks learning/teaching approach for first and second grace place value and multidigit additions and subtraction [El uso del enfoque de enseñanza/aprendizaje de bloques de base diez para el valor de la primera y la segunda posición and las sumas and restas de varios dígitos]. Journal for Research in Mathematics Education, 21, 180-206.

Geary, D. C. (January-February, 2004). Mathematics and learning disabilities [Matemáticas y dificultades de aprendizaje]. Journal of Learning Disabilities, 37(1), 4-15. Retrieved from https://web.missouri.edu/~gearyd/JLD04.pdf

Geary, D. C., & Hoard, M. K. (2001). Numerical and arithmetical deficits in learning-disabled children: Relation to dyscalculia and dyslexia [Déficits numéricos y aritméticos en niños con problemas de aprendizaje: Relación con la discalculia y la dislexia]. Aphasiology, 15(7), 635-647. doi: 10.1080/02687040143000113

Giménez, J. (1999). Ensenyament i aprenentatge de les matemàtiques: temes clau [Teaching and learning of mathematics: Key topics]. In C. A. Català, (Ed.), Psicopedagogia de les matemàtiques [Mathematics Psychopedagogy] (pp. 97-168). Barcelona: Universitat Oberta de Catalunya.

González, L. J. (2012). El conocimiento y uso de estrategias metodológicas apoyadas en las TIC para mejorar el proceso de enseñanza-aprendizaje del área de matemáticas en la educación primaria. [Knowledge and use of ICT methodological strategies to improve the teaching-learning process in the mathematics area in primary school]. In F. Guerra, R. García-Ruiz, N. González, P. Renés and A. Castro (Coords.), Estilos de aprendizaje: Investigaciones y experiencias [Learning styles: Research and Experiences] (pp. 1-13). Santander: Universidad de Cantabria. Retrieved from http://dialnet.unirioja.es/servlet/libro?codigo=555496

Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis [El conocimiento conceptual y procedimental en matemáticas: Un análisis introductorio]. In J. Hiebert (Ed.), Conceptual and procedural knowledge: the case of mathematics [El conocimiento conceptual y procedimental: El caso de las matemáticas] (pp. 1-27). Hillsdale: Lawrence Erlbaum Associates.

Hiebert, J., & Lindquist, M. M. (1990). Developing mathematical knowledge in the young child [Desarrollando el conocimiento matemático en el niño pequeño]. In J. N. Payne (Ed.) Mathematics for the young child [Matemáticas para niños pequeños] (pp. 17-36). Reston: National Council of Teachers of Mathematics.

Hiebert, J., & Wearne, D. (1996). Instruction, understanding, and skill in multidigit addition and subtraction [Instrucción, comprensión y habilidades, en la suma y resta de varios dígitos]. Cognition and Instruction, 14(3), 251-283. Retrieved from http://www.jstor.org/ stable/3233650?seq=1#page_scan_tab_contents

Jonassen, D. H. (1997). Instructional design models for well-structured and ill-structured problem-solving learning outcomes [Modelos de diseño instruccional para resultados de aprendizaje de resolución de problemas bien estructurados y mal estructurados]. Educational Technology: Research and Development, 45(1), 65-95. Retrieved from http://download.springer.com/static/pdf/446/art%253A10.1007%252FBF02299613. pdf?originUrl=http%3A%2F%2Flink.springer.com%2Farticle%2F10.1007%2FBF0229961 3&token2=exp=1445276790~acl=%2Fstatic%2Fpdf%2F446%2Fart%25253A10.1007%25 252FBF02299613.pdf%3ForiginUrl%3Dhttp%253A%252F%252Flink.springer.com%252F article%252F10.1007%252FBF02299613*~hmac=f1237b25866047f552b278773f12c91b 9b0c196fad2e130887ead75a213510b9

Landerl, K., Bevan, A., & Butterworth, B. (September, 2004). Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. [Discalculia del desarrollo y capacidades numéricas básicas: Un estudio de estudiantes de 8-9 años de edad]. Cognition, 93(2), 99-125. doi: 10.1016/j.cognition.2003.11.004

López, R., & Sánchez, A. B. (2006). Adquisición del error en la sustracción en educación primaria. [Error acquisition in subtraction in primary school]. In J. J. Navarro and M. Aguilar (Eds.), Libro de actas del Simposio Internacional sobre Matemática Temprana [Minutes from the International Symposium on Early Mathematics] (pp. 12-59). Departamento de Psicología de la Universidad de Cádiz: Cádiz.

López, R., & Sánchez, A. B. (September-December, 2007). Los componentes generadores de errores algorítmicos. Caso particular de la sustracción [The generating components of algorithm error. Particular case of subtraction]. Revista de Educación, 344, 377-402. Retrieved from http://www.revistaeducacion.mec.es/re344/re344_16.pdf

López, R., & Sánchez, A. B. (March, 2009). Los desarrollos hipermedia y el aprendizaje de la resta. [Hipermedia and learning subtraction]. Revista Iberoamericana de educación matemática [Ibero-American Journal of Mathematics Education], 17, 17-30. Retrieved from http://www.fisem.org/www/union/revistas/2009/17/Union_017_006.pdf

Marcelo, C. (June, 2001). Rediseño de la práctica pedagógica: Factores, condiciones y procesos de cambios en los teletransformadores [Redesigning the pedagogical practice: change factors, conditions, and process in teletransformers]. Conferencia presentada en la Reunión Técnica Internacional sobre el uso de TIC en el Nivel de Formación Superior Avanzada, Sevilla.

Martin, J., & VanLehn, K. (1995). Student assessment using bayesian nets [Evaluación de alumnos utilizando redes bayesianas]. Human-Computer Studies, 42, 575-591. Retrieved from http:// www.public.asu.edu/~kvanlehn/Stringent/PDF/95IJHCS_JM_KVL.pdf

Noda, A., & Bruno, A. (2009). Conceptos, estrategias y errores en las operaciones de suma y resta en alumnos con Síndrome de Down [Concepts, strategies, and errors in adding and subtraction in students with Down Syndrome]. In M. J. González, M.T. González, J. Murillo (Coords.), Investigación en educación matemática XIII [Research on Mathematical Education] (pp. 333-343). Santander: Sociedad Española de Investigación en Educación Matemática, SEIEM. Retrieved from http://dialnet.unirioja.es/ descarga/articulo/3629063.pdf

Ohlsson, S., & Rees, E. (1991). The function of conceptual understanding in the learning of arithmetic procedure [La función de la comprensión de los conceptos en el aprendizaje de procedimientos aritméticos]. Cognition and Instruction, 8(2) 103-179.

Peltenburg, M., van den Heuvel-Panhuizen, M., & Robitzsch, A. (2010). ICT-based dynamic assessment to reveal special education students’ potential in mathematics [Evaluación dinámica basada en las TIC para revelar el potencial de los estudiantes de educación especial en matemáticas]. Research Papers in Education, 25(3), 319-334.

Resnick, L. (1982). Syntax and semantics in learning to substract [Sintaxis and semántica en el aprendizaje de la resta]. In T. Carpenter, J. Moser and T. Romberg (Eds.), Addition and subtraction: A cognitive perspective [Suma y resta: Una perspectiva cognitiva] (pp. 136-175). Hillsdale: Lawrence Erlbaum Associates.

Resnick, L. (1983). A developmental theory of number understanding [Una teoría del desarrollo de la comprensión de los números] H. P. Ginsburg (Ed.), The development of mathematical thinking [El desarrollo del pensamiento matemático] (pp. 109-151). New York: Academic Press.

Resnick, L., & Omanson, S. F. (1987). Learning to understand arithmetic [El aprendizaje para comprender la aritmética]. In R. Glaser (Ed.), Advances in instructional psychology [Los avances en la psicología de la instrucción] (pp. 41-95). Hillsdale: Lawrence Erlbaum Associates.

Robinson, K. (March, 2001). The validity of verbal reports in children’s subtraction [La validez de los informes verbales de la resta en los niños]. Journal of Educational Psychology, 93(1), 211-222.

Rosselli, M., & Matute, E. (2005). Neuropsychologie de la dyscalculie développementale: Derniers résultats de recherche en Amérique du Nord [Neuropsychology of the development of dyscalculia: Results of the latest research in North America] In A. Van Hout, and C. Meljac (Eds.), Troubles du calcul et dyscalculies chez l’enfant [Trastornos del cálculo y discalculias en niños] (pp. 175-185). París: Masson.

Sánchez, A. B., & López, R. (January-April, 2009). La transferencia de aprendizaje algorítmico y el origen de los errores en la sustracción [The transference of algorithm and the origin of errors of subtraction]. Revista de educación, 354, 429-445. Retrieved from http://www.revistaeducacion.mec.es/re354/re354_17.pdf

Shalev, R. S., & Gross-Tsur, V. (Mayo, 2001). Developmental dyscalculia. Review article [Desarrollo de la discalculia. Artículo de revisión]. Pediatric Neurology, 24(5), 337-342.

Siegler, R. S. (1987). Strategy choices in subtraction [La selección de estrategias en la resta]. In J. A. Sloboda and D. Rogers (Eds.), Cognitive processes in mathematics [Procesos cognitivos en matemáticas] (pp. 81-106). Oxford: Oxford University Press.

Siegler, R. S., & Jenkins, E. (1989). How children discover new strategies [Cómo es que los niños descubren nuevas estrategias]. Hillsdale: Eribaum.

VanLehn, K. (1982). Bugs are not enough: Empirical studies of bugs, impasses and repairs in procedural skills [Los errores no son insuficientes: Estudios empíricos de los errores, impasses y modificaciones en las habilidades procedimentales] Journal of Mathematical Behaviour, 3(2), 3-71. Retrieved from http://www.public.asu.edu/~kvanlehn/Stringent/PDF/ BugsAreNotEnough1982.pdf

VanLehn, K. (1983). Human procedural skill acquisition: Theory, model and psychological validation [La adquisición de los procedimientos: Teoría, modelo y validación psicológica]. In P. Langley (Ed.), Proceedings of the 1983 Conference of the American Association for Artificial Intelligence [Actas de la Conferencia de la Asociación Americana para la Inteligencia Artificial de 1983] (pp. 420-423). Los Altos: Morgan Kaufmann. Retrieved from http://www. public.asu.edu/~kvanlehn/Stringent/PDF/83AAAI_KVL.pdf

VanLehn, K. (1987). Learning one subprocedure per lesson [Aprendizaje de un subprocedimiento por lección]. Artificial Intelligence, 31, 1-40. http://www.public.asu.edu/~kvanlehn/ Stringent/PDF/87AI_KVL.pdf

VanLehn, K. (1990). Mind bugs: origins of procedural misconceptions [Los errores principales: Orígenes de los procedimientos erróneos]. Cambridge: MIT Press.

Waiganjo, S., & Wausi, A. (2013). Using ICT to assist dyscalculia students: situation analysis for primary schools in Kenya, a case study of Starehe District Nairobi County [El uso de las TIC para ayudar a los estudiantes con discalculia: Análisis de la situación de las escuelas de Kenya, un estudio de caso del distrito Starehe de Nairobi]. International Journal of Innovative Education Research, 1(1), 74-83. Retrieved from http://sci.uonbi.ac.ke/node/2250

Young, R. M., & O’Shea, T. (April, 1981). Errors in children’s subtraction [Errores de los niños en la sustracción] Cognitive Science, 5(2), 153-177. doi: 10.1207/s15516709cog0502_3

---