Revista Electrónica Educare (Educare Electronic Journal) EISSN: 1409-4258 Vol. 20(3) SETIEMBRE-DICIEMBRE, 2016: 1-18

doi: http://dx.doi.org/10.15359/ree.20-3.9

URL: http://www.una.ac.cr/educare

CORREO: educare@una.cr

[Número publicado el 01 de setiembre del 2016]

---

 

Analyzing the Measurement Equivalence of a Translated Test in a

Statewide Assessment Program

Análisis de la equivalencia de la medida de la traducción de un test

en un programa de evaluación estatal

Jorge Carvajal-Espinoza1

Universidad de Costa Rica

San José, Costa Rica

correo: jorge.carvajalespinoza@ucr.ac.cr

orcid: http://orcid.org/0000-0003-0204-4894

Greg W. Welch2

University of Nebraska, Lincoln

Lincoln, Nebraska, Estados Unidos

gwelch2@unl.edu

Recibido 30 de junio de 2015 • Corregido 5 de julio de 2016 • Aceptado 16 de agosto de 2016

Abstract. When tests are translated into one or more languages, the question of the equivalence of items across language forms arises. This equivalence can be assessed at the scale level by means of a multiple group confirmatory factor analysis (CFA) in the context of structural equation modeling. This study examined the measurement equivalence of a Spanish translated version of a statewide Mathematics test originally constructed in English by using a multi-group CFA approach. The study used samples of native speakers of the target language of the translation taking the test in both the source and target language, specifically Hispanics taking the test in English and Spanish. Test items were grouped in twelve facet-representative parcels. The parceling was accomplished by grouping items that corresponded to similar content and computing an average for each parcel. Four models were fitted to examine the equivalence of the test across groups. The multi-group CFA fixed factor loadings across groups and results supported the equivalence of the two language versions (English and Spanish) of the test. The statistical techniques implemented in this study can also be used to address the performance on a test based on dichotomous or dichotomized variables such as gender, socioeconomic status, geographic location and other variables of interest.

Keywords. Measurement equivalence, structural equation modeling, confirmatory factor analysis.

Resumen. Al traducir tests a uno o más lenguajes, surge la pregunta sobre la equivalencia de los ítems en los diferentes lenguajes. Esta equivalencia puede ser estudiada en el nivel de escala por medio de un análisis factorial confirmatorio (AFC) de grupos múltiples en el contexto de modelos de ecuaciones estructurales. Esta investigación analizó la equivalencia de la medida de la versión en español de un test construido originalmente en inglés utilizando un AFC de grupos múltiples. Se utilizaron muestras de hablantes nativos del idioma al que se tradujo el test, quienes tomaron el test en inglés y en español, específicamente hispanoparlantes. Los ítems del test fueron agrupados en 12 conjuntos de contenido similar y para cada conjunto se calculó un promedio. Cuatro modelos fueron analizados para examinar la equivalencia entre grupos. Los pesos factoriales y los resultados obtenidos en las dos versiones del test (español e inglés) sugieren la equivalencia de ambas versiones. Las técnicas estadísticas utilizadas en este estudio pueden asimismo ser usadas para analizar el desempeño en un test con base en variables dicotómicas o que pueden tratarse como dicotómicas como género, estatus socioeconómico, localización geográfica y otras variables de interés.

Palabras claves. Equivalencia de la medida, modelos de ecuaciones estructurales, análisis factorial confirmatorio.

Introduction

Many states are offering versions of their statewide test forms in alternate languages as an accommodation for English Language Learners (ELLs) typically a Spanish-language version or other available home-language version of the assessment as the No Child Left Behind (NCLB) Act allows for any student who has not been in the United States for three consecutive years to be assessed with certain accommodations. Prior to the legislation of NCLB, ELLs were not included in statewide testing programs which resulted in a lack of accountability for the academic progress of these students (Lara & August, 1996). Students who had been in the United States or in an ESL program for less than 3 years were exempt from testing in most states (Holmes, Hedlund & Nickerson, 2000). The consequence was that ELLs did not benefit from the implementation of a state’s standardized assessment program and from educational programs and reforms intended to promote student learning (August & Hakuta, 1997). As ELLs are now being included in statewide testing programs, various types of accommodations may be allowed when the tests are is administered.

Language-specific accommodations, for example, are changes in the test or testing situation that address and consider a non-native speaker’s unique linguistic needs. The use of accommodations is intended to “level the playing field” and make assessment fair to all students. The idea is that with appropriate accommodations, a student’s ELL status should no longer be a hindrance to his/her true demonstration of knowledge. Accommodations include adaptations to testing that do not change the intent, purpose, or content of the test and do not provide the student with an unfair advantage. These adaptations do not interfere with scoring, they do not violate test security or the substantive focus of the assessment. Accommodations are especially important and appropriate in states with small but growing numbers of Hispanic students where Spanish test versions are common. The need for alternative forms to address federal accountability requirements has put a spotlight directly on test translation and test validity.

When tests are translated into one or more languages, the question of the equivalence of items across language forms arises (Price, 1999). There are two common applications for identifying potential bias against groups of examinees on a test. These applications focus on a combination of professional judgments about the appropriateness and freedom from bias of program materials and the gathering and interpretation of statistical information about differential item functioning (DIF). The DIF methodology has been used as a means to evaluate this equivalence in many testing programs (Gierl, Rogers & Klinger, 1999; Robin, Sireci & Hambleton, 2003; Sireci & Khaliq, 2002). DIF is said to exist when examinees of equal ability differ, on average, according to their group membership in their responses to a particular item (American Educational Research Association, AERA, Asociación Americana de Psicología, APA & National Coucil on Measurement in Education, NCME, 2014).

Translation DIF literature has called for the examination of the equivalence of the construct structure across the original and the adapted forms (Robin et al., 2003). This equivalence can be assessed at the scale level by means of a multiple group confirmatory factor analysis (CFA) in the context of structural equation modeling (SEM).

When such studies are conducted, extraneous factors can confound the results and thus confuse the findings. Potential causes include the translation itself (a poor quality translation or a translation at a different reading level, for example) or factors associated with group membership (cultural differences or differences in curricula, for example).

One possible way to control for this confounding is to analyze how the test behaves for samples of subjects of the target language taking the test in the source and the target language. In this way cultural differences can be ruled out and differences can be attributed to the translation itself.

While several studies have been conducted to analyze equivalence among different language versions of a test using a multiple group CFA (e.g. Wu, Li, and Zumbo (2007); Lievens, Anseel, Harris & Eisenberg, 2007) a void in the literature exists regarding studies that have used samples of native speakers of the target language of the translation taking the test in both the source and target language, for example, Hispanic ELLs taking the test in English and in Spanish.

The purpose of the present study is to examine the measurement equivalence of a statewide Mathematics test originally constructed in English and its Spanish translated version by using a multi-group CFA in the context of SEM (Byrne, 2006) utilizing samples of native speakers of the target language of the translation taking the test in both the source and target language. Specifically the subjects of the study are Hispanic ELLs. The existence of such samples is due to the fact that for this test, schools can assign to Hispanic ELLs either the English or Spanish version of the Mathematics test based on their English proficiency. In general, measurement equivalence exists if the probability of an observed score, given the true score, is independent of group membership (Wu et al., 2007; Hirschefeld & von Brachel, 2014). In our study, the group membership is determined by taking the test either in English or in Spanish.

Method

The translation of the assessment into Spanish from English was accomplished as follows. For each test, two translators independently conducted a translation of the assessment into Spanish. Subsequently, they performed a consensus-based validation of the translation. A third translator, proficient in both English and Spanish, then compared the English and the consensus-based version and made suggestions. The two first translators prepared a final version based upon those suggestions. All three translators were native Spanish speakers, with one of the translators being a mathematics educator.

The sample consisted of 957 ELLs, all 4th graders of Hispanic origin. Of the sample, 871 of the students were administered the 4th grade State Assessment in English while 86 took the Spanish-language translated version of that test.

In a previously conducted DIF study with this data set (Carvajal, 2015) two items out of 52 total items on the test where identified as showing DIF. These two items were eliminated from the present analysis in order to study the equivalence of the two versions after the DIF items had been removed.

The remaining 50 items were grouped in 12 facet representative parcels. The use of item parcels has advantages over the use of individual items as indicators for a variety of reasons, including keeping the ratio for manifest indicators to latent constructs manageable and reducing the number of free parameters in the model to decrease sample size requirements (Hall, Snell & Singer, 1999). The parceling was accomplished by grouping items that corresponded to similar content and computing an average for each parcel.

The test targets four content standards within the domain of Mathematics: Numbers, Algebra, Geometry, and Data. There are 3 parcels associated with each of these topics. Figure 1 below shows the distribution and parceling of the 50 items. For example, there are 11 items under the topic Geometry; these items were grouped in 3 parcels with 3, 4 and 4 items, respectively.

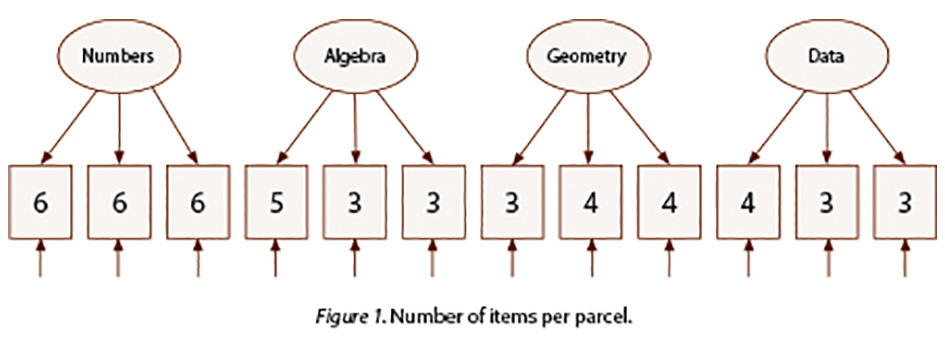
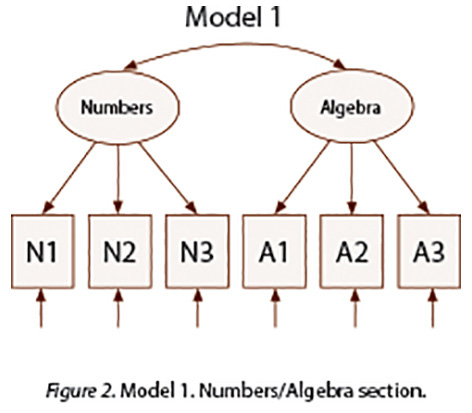
Although a model that includes the four standards would be the ideal model to be fitted across groups, due to relatively small sample size considerations (86 subjects in Spanish version) the decision was made to divide the test in two sections: Numbers and Algebra and Geometry and Data.

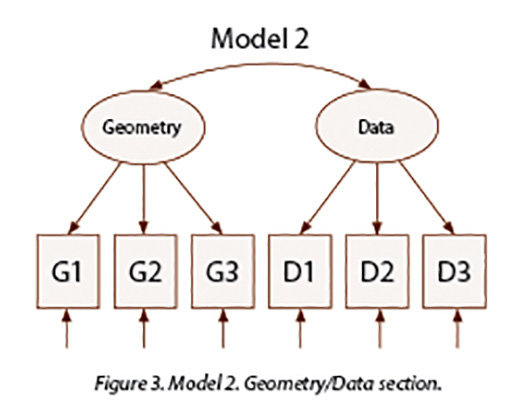
Figure 2 and Figure 3 display the models (Model 1 and Model 2) that were initially fitted. Further models were fitted as described in the results section.

The multiple group CFA analysis was conducted in EQS (Bentler, 1995). Fit indexes were evaluated in terms of the cutoff values proposed by Hu and Bentler (1999).

Results

Descriptive information

Table 1 provides descriptive information (Mathematics percent correct total score) on the samples of 4th grade ELL students by gender that took the Mathematics assessment in either the Spanish or English language format.

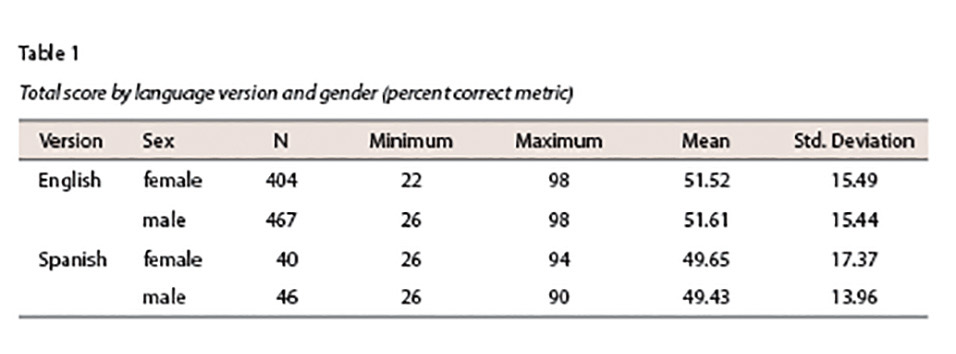
Table 1 indicates that within each language version, males and females performed comparably on the Mathematics assessment. Students in the Spanish language form scored approximately 2 percentage points lower than those students administered the English language form.

Table 2 and Table 3 provide a summary of total score (percent correct) information for the Numbers/Algebra and Geometry/Data sections, respectively.

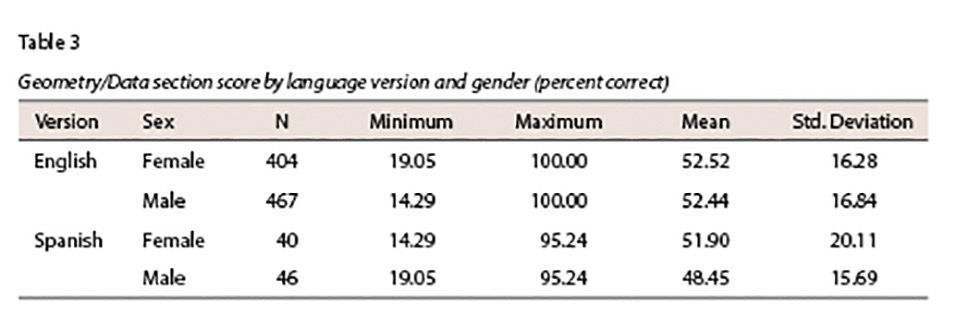
Table 2 and Table 3 indicate that for students administered the Spanish language version of the assessment, small differences in the percent correct mean score between males and females on the subtests are observed. Males tended to score higher, on average, than females on the Numbers/Algebra section while females performed slightly higher than males on the Geometry/Data section. As the samples size for these respective gender groups is small, they are more susceptible to variability.

Multiple group CFA results

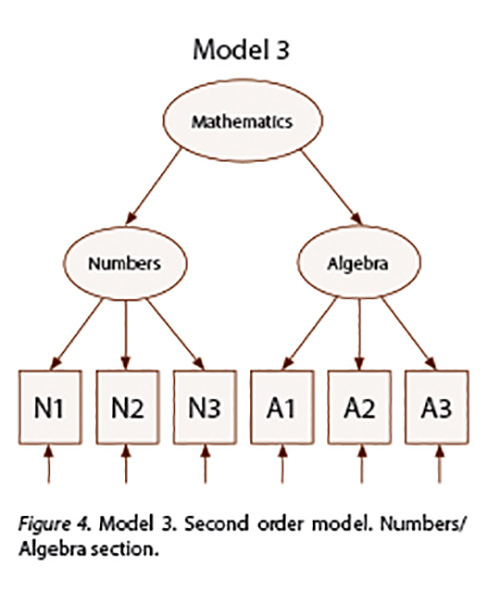
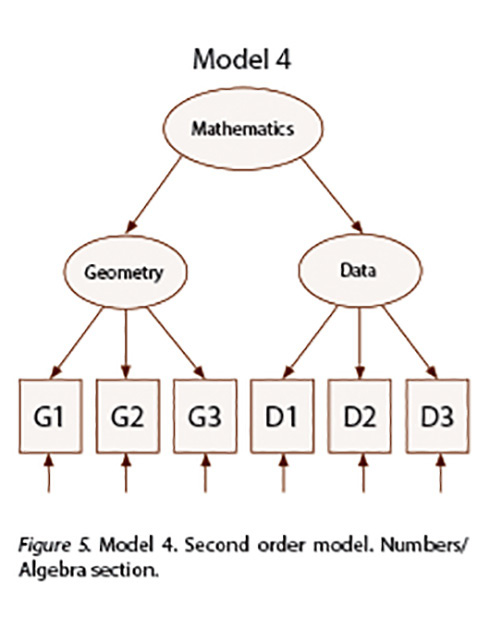
After fitting Model 1 and Model 2, high correlations were found between the two factors for both groups: r(Numbers, Algebra) = .90, r(Geometry, Data) = .97 in the English version and : r(Numbers, Algebra) = .79, r(Geometry, Data) = .77 in the Spanish version. These high correlations make sense because the test is ultimately built to measure Math knowledge. The values of correlation coefficients indicated a higher order model may be more appropriate. Accordingly, second order multiple group CFAs where Mathematics explains Numbers and Algebra (Model 3) and Geometry and Data (Model 4) were conducted. Figure 4 and Figure 5 display these two new models.

Model 3 results:

Appendix 1 displays the syntax used for fitting Model 3. As it can be noted the loading of Numbers on parcel N1 and the loading of Algebra on parcel A1 were fixed to 1. The remaining 6 loadings (Numbers on parcels N2 and N3, Algebra on parcels A2 and A3, Mathematics on Numbers and Math on Algebra) were estimated and then constrained to be equal across the two groups (Hispanics taking the English version and Hispanics taking the Spanish version) in order to test the model equivalence.

According to the analysis of the contribution to normalized multivariate kurtosis, case 512 of the English version group was deemed an outlier and eliminated. The Mardia’s coefficient and its normalized indicated no significant excess kurtosis indicative of non-normality; therefore the maximum likelihood solution (normal distribution theory) is reported.

The normal distribution theory goodness of fit indices indicate model equivalence across groups. Chi-square is 33.9164 with 21 degrees of freedom, p= .03700 showing that the null hypothesis that the model is equivalent across groups is rejected. This result came as no surprise as it is well known that this Chi-square statistic is extremely sensitive to sample size. On the other hand, other fit indices show that the constraints hold across groups as all are greater than the standard 0.95 (Hu & Bentler, 1999): Comparative fit index (CFI) = .987, Joreskog-Sorbom’s GFI = .989 and Joreskog-Sorbom’s AGFI=.977. Additionally, the root mean-square error of approximation was less than .05 (RMSEA = .036), which indicates that the constraints hold. The RMSEA 90% confidence interval is (.009, .058) which also supports the equality of loadings across groups.

Model 4 results:

Appendix 2 displays the syntax used for fitting Model 4. In a similar fashion to Model 3, it can be noted that the loading of Geometry on parcel G1 and the loading of Data on parcel D1 were fixed to 1. The remaining 6 loadings (Geometry on parcels G2 and G3, Data on parcels D2 and D3, and Mathematics on Geometry and Mathematics on Data) were estimated and then constrained to be equal in order to test the model equivalence across groups.

According to the analysis of the contribution to normalized multivariate kurtosis no outliers were found. The Mardia’s coefficient and its normalized estimate indicated no excess kurtosis indicative of non-normality; therefore the maximum likelihood solution (normal distribution theory) is reported.

The normal distribution theory goodness of fit indices indicate model equivalence across groups. Chi-square is 19.661 with 20 degrees of freedom, p= .47932 indicating that the null hypothesis that the model is equivalent across groups is not rejected. Other fit indices also show that the constrains hold across groups as CFI = 1.000, GFI = .993, and AGFI=.986. All exceed the standard .95. In addition, RMSEA = .000, which is less than .05, therefore indicating that the constraints hold. The RMSEA 90% confidence interval is (.000, .039) which also supports the equality of loadings across groups.

An additional note on the rejection of the null hypothesis that appears in model 3 but not in model 4 is necessary. Given the results of the other fit indices, our overall assessment is that both models 3 and 4 fit the data. The normal chi-square statistic cannot be relied upon for the rejection of the null hypothesis due to its dependence on sample size. Hence we interpreted the rejection of the null hypothesis in model 3 as an instance of Type I error.

It is also worth mentioning the difference between models 1 and 3 and 2 and 4, as models 3 and 4 appear to be appropriate given that the factors in model 1 and 2 are highly correlated and given the way in which the assessment is structured.

Discussion

The purpose of the current study was to examine the measurement equivalence of a Spanish translated version of a statewide Mathematics test originally constructed in English by using a multi-group CFA approach. The CFA approach, in general, is a powerful method for addressing measurement invariance in the context of standardized assessment programs. The multi-group CFA, as implemented in this study, fixed factor loadings across groups to examine the equivalence of English and Spanish versions of a standardized assessment. The results supported the equivalence of the two language versions of the test.

Two common approaches exist for examining bias or the quality of a test translation. While professional reviews have great utility, empirical techniques offer a level of precision that is not supplied by judgments. This study offered a statistical methodology for evaluating the quality of a translation. It utilized the comparison between native speakers of the target language taking the test in the source and the target language. This comparison has not been researched adequately and this study attempted to address the void in the test adaptation literature. Furthermore, we believe that this comparison can provide important information in the process of adapting tests. The suggested technique may provide more informative results than the traditional approach that only compares native speakers of the source language to native speakers of the target language, so long as appropriate samples are available.

Once structural equivalence of a construct has been demonstrated between native speakers of the target language, it is important to test the measurement equivalence between native speakers of the source language and the target language. If the latter is not supported, there is reason to think that there are cultural factors causing the lack of equivalence. For the test analyzed in the current study, it was not possible to carry this out because the English version that is offered to ELLs is a simplified language version compared to the English version that U.S. native speakers take.

Relatively small sample size in the group that took the test in Spanish tempers generalizability somewhat, but with the particular test type and subgroup, this will always be an issue. While additional studies with larger sample sizes would be ideal to replicate and validate the model presented in this study, the technique detailed in the current study is viable and is promising for assessing the measurement equivalence of translated tests in a statewide assessment program.

The importance of addressing measurement equivalence cannot be overstated. Assessment programs will always be faced with the challenge of creating culturally appropriate forms in multiple languages, especially in the United States where there exists an influx of Spanish speaking students. Given the importance of assessing learning through a rigorous assessment program, the most current and advanced developments in methodology must be implemented to address important issues such as measurement equivalence. Students that speak English as a second language are often at a disadvantage in the classroom to begin with, therefore, approaches to assessing their learning should rule out all bias associated with the assessment process itself. This study offers knowledge which can be built upon to further our understanding of measurement equivalence in standardized assessment programs.

The statistical techniques utilized in this study can also be used to address the performance on a test based on dichotomous or dichotomized variables such as gender, socioeconomic status, geographic location and other variables of interest. These variables can, and should, be examined in the context of populations that speak English as a second language. Many Spanish speaking students come from low to lower income families which provides an additional obstacle for them to overcome. A better understanding of this factor can also be instrumental in developing assessments that are fair for all. In addition, the statistical technique illustrated in this study can be used with such variables in other research contexts where measurement equivalence is also of interest.

Future research should also consider methodological approaches for addressing measurement equivalence when one group is much smaller than the other. Bias in estimates can exist when comparisons are being made between groups of students that are very small by comparison. This must be a strong consideration in any future work conducted in this area.

Referencias

American Educational Research Association (AERA), Asociación Americana de Psicología (APA), & National Coucil on Measurement in Education (NCME). (2014). Standards for educational and psychological testing. Washington, DC: American Educational Research Association.

August, D., & Hakuta, K. (Eds.). (1997). Improving schooling for language-minority students. A research agenda. Washington, DC: National Academy of Science.

Bentler, P. M. (1995). EQS: Structural equations program manual. Encino, CA: Multivariate Software.

Byrne, B. M. (2006). Structural equation modeling with EQS: Basic concepts, applications, and programming. Mahwah, NJ: Lawrence Erlbaum. doi: http://dx.doi.org/10.1207/s15328007sem1302_7

Carvajal, J. (2015). Using DIF to monitor equivalence of translated tests in large scale assessment: A comparison of native speakers in their primary and the test’s source language. The Tapestry Journal, 7(1), 14-21. Recuperado de http://journals.fcla.edu/tapestry/article/view/88133/84742

Gierl, M., Rogers, W. T., & Klinger, D. A. (1999). Using statistical and judgmental reviews to identify and interpret translation differential item functioning. The Alberta Journal of Educational Research, 45(4), 353-376. Recuperado de http://ajer.journalhosting.ucalgary.ca/index.php/ajer/article/view/107/99

Hall, R. J., Snell, A. F., & Singer M. (1999). Item parceling strategies in SEM: Investigating the subtle effects of unmodeled secondary constructs. Organizational Research Methods, 2(3), 233-256. doi: http://dx.doi.org/10.1177/109442819923002

Hirschfeld, G., & von Brachel, R. (2014). Multiple-Group confirmatory factor analysis in R-A tutorial in measurement invariance with continuous and ordinal indicators. Practical Assessment, Research & Evaluation, 19(7), 1-12. Recuperado de http://pareonline.net/pdf/v19n7.pdf

Holmes, D., Hedlund, P., & Nickerson, B. (2000). Accommodating ELLs in state and local assessments. Washington, DC: National Clearinghouse for Bilingual Education.

Hu, L. & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structual Equation Modeling, 6(1), 1-55. doi: http://dx.doi.org/10.1080/10705519909540118

Lara, J., & August, D. (1996). Systemic reform and limited English proficient students. Washington, DC: Council of Chief State School Officers.

Lievens, F., Anseel, F., Harris, M. M., & Eisenberg, J. (2007). Measurement invariance of the Pay Satisfaction Questionnaire across three countries. Educational and Psychological Measurement, 67(6), 1042-1051. doi: http://dx.doi.org/10.1177/0013164406299127

Price, L. R. (1999). Differential functioning of items and tests versus the Mantel-Haenszel technique for detecting differential item functioning in a translated test. Paper presented at the annual meeting of the American Alliance of Health Physical Education, Recreation, and Dance. Boston, MA.

Robin, F., Sireci, S. G., & Hambleton, R. (2003). Evaluating the equivalence of different language versions of a credentialing exam. International Journal of Testing, 3(1), 1-20. doi: http://dx.doi.org/10.1207/S15327574IJT0301_1

Sireci, S. G., & Khaliq, S. N. (April, 2002). An analysis of the psychometric properties of dual language test forms. (Center for Educational Assessment, Report No. 458). Paper presented at the Annual Meeting of the National Council on Measurement in Education. Amherst: University of Massachusetts, School of Education. Recuperado de http://files.eric.ed.gov/fulltext/ED468489.pdf

Wu, A. D., Li, Z., & Zumbo, B. D. (2007). Decoding the meaning of factorial invariance and updating the practice of multi-group confirmatory factor analysis: A demonstration with TIMSS data. Practical Assessment, Research and Evaluation, 12(3), 1-26. Recuperado de http://pareonline.net/getvn.asp?v=12&n=3

Apendix 1

/TITLE

Measurement Invariance for Hispanic ELL: English/Spanish Version of a Math Test - Model 3

Group 1 - Hispanics who took the test in English. Numbers and Algebra Section.

/SPECIFICATIONS

DATA=’C:\NCME\4ghe.ess’;

VARIABLES=12; CASES=871; DEL=512; Groups=2;

METHOD=ML,ROBUST; ANALYSIS=COVARIANCE; MATRIX=RAW;

/LABELS

V1=N1; V2=N2; V3=N3; V4=A1; V5=A2;

V6=A3; V7=G1; V8=G2; V9=G3; V10=Da1;

V11=Da2; V12=Da3;

F1=Numbers; F2=Algebra; F3=Math;

/EQUATIONS

V1 = 1F1 + E1;

V2 = *F1 + E2;

V3 = *F1 + E3;

V4 = 1F2 + E4;

V5 = *F2 + E5;

V6 = *F2 + E6;

F1= *F3 + D1;

F2= *F3 + D2;

/VARIANCES

F3=1;

D1 to D2 = *;

E1 to E6 = *;

/PRINT

FIT=ALL;

TABLE=COMPACT;

/TECHNICAL

/END

/TITLE

Measurement Invariance for Hispanic ELL: English/Spanish Version of a Math Test - Model 3

Group 2 - Hispanics who took the test in Spanish. Numbers and Algebra Section.

/SPECIFICATIONS

DATA=’C:\NCME\4ghs.ess’;

VARIABLES=12; CASES=86;

METHOD=ML,ROBUST; ANALYSIS=COVARIANCE; MATRIX=RAW;

/LABELS

V1=N1; V2=N2; V3=N3; V4=A1; V5=A2;

V6=A3; V7=G1; V8=G2; V9=G3; V10=Da1;

V11=Da2; V12=Da3;

F1=Numbers; F2=Algebra; F3=Math;

/EQUATIONS

V1 = 1F1 + E1;

V2 = *F1 + E2;

V3 = *F1 + E3;

V4 = 1F2 + E4;

V5 = *F2 + E5;

V6 = *F2 + E6;

F1= *F3 + D1;

F2= *F3 + D2;

/VARIANCES

F3=1;

D1 to D2 = *;

E1 to E6 = *;

/PRINT

FIT=ALL;

TABLE=COMPACT;

/CONSTRAINTS

(1,V2,F1) = (2,V2,F1);

(1,V3,F1) = (2,V3,F1);

(1,V5,F2) = (2,V5,F2);

(1,V6,F2) = (2,V6,F2);

(1,F1,F3) = (2,F1,F3);

(1,F2,F3) = (2,F2,F3);

TECHNICAL

/LMTEST

/END

Appendix 2

/TITLE

Measurement Invariance for Hispanic ELL: English/Spanish Version of a Math Test - Model 4

Group 1 - Hispanics who took the test in English. Geometry and Data Section

/SPECIFICATIONS

DATA=’C:\NCME\4ghe.ess’;

VARIABLES=12; CASES=871; Groups=2;

METHOD=ML,ROBUST; ANALYSIS=COVARIANCE; MATRIX=RAW;

/LABELS

V1=N1; V2=N2; V3=N3; V4=A1; V5=A2;

V6=A3; V7=G1; V8=G2; V9=G3; V10=Da1;

V11=Da2; V12=Da3;

F1=Geometry; F2=Data; F3=Math;

/EQUATIONS

V7 = 1F1 + E1;

V8 = *F1 + E2;

V9 = *F1 + E3;

V10 = 1F2 + E4;

V11 = *F2 + E5;

V12 = *F2 + E6;

F1= *F3 + D1;

F2= *F3 + D2;

/VARIANCES

F3=1;

D1 to D2 = *;

E1 to E6 = *;

/PRINT

FIT=ALL;

TABLE=COMPACT;

/TECHNICAL

/END

/TITLE

Measurement Invariance for Hispanic ELL: English/Spanish Version of a Math Test - Model 4

Group 2 - Hispanics who took the test in Spanish. Geometry and Data Section

/SPECIFICATIONS

DATA=’C:\NCME\4ghs.ess’;

VARIABLES=12; CASES=86;

METHOD=ML,ROBUST; ANALYSIS=COVARIANCE; MATRIX=RAW;

/LABELS

V1=N1; V2=N2; V3=N3; V4=A1; V5=A2;

V6=A3; V7=G1; V8=G2; V9=G3; V10=Da1;

V11=Da2; V12=Da3;

F1=Geometry; F2=Data; F3=Math;

/EQUATIONS

V7 = 1F1 + E1;

V8 = *F1 + E2;

V9 = *F1 + E3;

V10 = 1F2 + E4;

V11 = *F2 + E5;

V12 = *F2 + E6;

F1= *F3 + D1;

F2= *F3 + D2;

/VARIANCES

F3=1;

D1 to D2 = *;

E1 to E6 = *;

/PRINT

FIT=ALL;

TABLE=COMPACT;

/CONSTRAINTS

(1,V8,F1) = (2,V8,F1);

(1,V9,F1) = (2,V9,F1);

(1,V11,F2) = (2,V11,F2);

(1,V12,F2) = (2,V12,F2);

(1,F1,F3)= (2,F1,F3);

(1,F2,F3)= (2,F2,F3);

TECHNICAL

/LMTEST

/END

---