Tabla de volumen comercial para teca clonal
en diferentes índices de sitio en la Zona Norte
de Costa Rica

Table of commercial volume for clonal teak at different
site indices in Northern Costa Rica

Katherine Barrantes-Madrigal1; Rafael Murillo-Cruz2; Carlos Ávila-Arias3; William Fonseca-González4; Ana Isabel Barquero-Elizondo5

[Recibido: 4 de mayo 2020, Aceptado: 28 de agosto 2020, Corregido: 18 de setiembre 2020, Publicado: 1 de enero 2021]

Resumen

[Introducción]: Es necesario cuantificar y predecir con confiabilidad el volumen de madera para facilitar la gestión de la producción forestal. [Objetivo]: Elaborar tablas de volumen comercial a partir de la selección de modelos matemáticos en distintas calidades de sitio, para plantaciones clonales de Tectona grandis L.f. [Metodología]: Se evaluaron 3 calidades de sitio, según el índice de sitio (IS) 27, 24 y 21, respectivamente. A 266 árboles en pie (119 árboles para el IS27, 119 para el IS24 y 28 para el IS21) se les midió el diámetro al tocón y a 1.3 m sobre el nivel del suelo. Posteriormente, cada 1.5 m, hasta completar la altura total. El volumen del árbol se obtuvo mediante la sumatoria de cada sección cubicada con la fórmula de Smalian. Para cada índice de sitio, se ajustaron modelos por el método de mínimos cuadrados ordinarios con el paquete estadístico Statgraphics Centurion XVI. Se verificó el cumplimiento de los supuestos de autocorrelación de los residuos mediante la prueba de Durbin-Watson. La selección del modelo se hizo a partir de la sumatoria basada en la normalización de los parámetros estadísticos evaluados. [Resultados]: Los modelos seleccionados tuvieron buenos ajustes (R2≥ 94 %), bajos errores de estimación (≤ 3 %), muy prácticos por usar solo el diámetro normal (DAP) como variable predictora. [Conclusiones]: Junto con la tabla de volumen comercial construida, los modelos son una herramienta útil para cuantificar, de forma rápida y precisa, el volumen comercial con corteza de teca clonal hasta 15 cm de diámetro mínimo.

Palabras clave: Clones; ecuaciones de volumen; tabla de volumen; Tectona grandis.

Abstract

[Introduction]: Reliably quantifying and predicting the volume of wood is essential to assist in forest production management. [Objective]: Generate commercial volume tables using the selected mathematical models at different site qualities for clonal plantations of Tectona grandis. [Methodology]: Three site qualities were evaluated according to site indices (SI) 27, 24, and 21, respectively. The diameter of 266 standing trees (119 for SI27, 119 for SI24, and 28 for SI21) was measured at the stump, 1.3 m above ground level, and every 1.5 m until the total height. The volume of the tree was obtained by adding each measured section with the Smalian formula. For each site index, models were adjusted by the ordinary least squares method using the Statgraphics Centurion XVI statistical package. The Durbin-Watson test verified compliance with the assumptions of autocorrelation of residuals. The model was selected based on the sum of the normalization of the statistical parameters evaluated. [Results]: The selected models had good adjustments (R2≥ 94 %) and low estimation errors (<3 %) and were very practical since they only use the normal diameter (DBH) as a predictor variable. [Conclusions]: Along with the table of commercial volume, the models are an important tool to quickly and accurately quantify the commercial volume of clonal teak with bark up to 15 cm in diameter.

Keywords: Clones; Tectona grandis, volume equations; volume table.

1. Introducción

La teca (Tectona grandis L. F.) es una de las especies maderables más importantes, con cerca de 6.8 millones de hectáreas (ha) plantadas alrededor del mundo (Madeiros et al., 2018). En Costa Rica, es la especie forestal más utilizada en la reforestación comercial con 47 167 ha (Instituto Nacional de Estadística y Censos –INEC-, 2015), debido, principalmente, a las excelentes propiedades de durabilidad y a la calidad de la madera, buen crecimiento e idoneidad para una gran variedad de usos (Ladrach, 2009; Mora y Hernández, 2007). Lo anterior, ha propiciado su creciente demanda del mercado y la consecuente expansión del cultivo intensivo (Fallas, 2017; Pérez y Kanninen, 2007).

El manejo de plantaciones, además del valor de la madera, requiere de la conjunción de aspectos silviculturales, genéticos y culturales, que garanticen la máxima productividad al menor costo (Moret et al., 1998). Esto es aplicable a cualquier sistema de producción forestal y para lograrlo se necesita de información técnica, especialmente, cuando se maneja una plantación para obtener productos de alto valor comercial (Sianturi, 2015; Ureigho y Akpobome, 2018).

Dada la urgencia de aumentar la productividad, el uso de material genético de calidad superior (clones seleccionados), propicia mejores rendimientos que el método de semilla (Badilla y Murillo, 2017; Fallas, 2017), sin suponer que este aspecto pueda lograr el objetivo final por sí mismo.

Al respecto, además de las prácticas culturales de manejo y el material genético, la calidad del sitio influye en el crecimiento de los árboles, y, por ende, en la producción (Armijos, 2013; Michone et al., 2017). Para T. grandis los mejores sitios para su establecimiento se ubican en terrenos de menos de 1000 msnm, en suelos con pendientes no mayores a 30 %. Los suelos poco profundos, arcillosos, planos, y con bajo contenido de calcio (Ca), magnesio (Mg) y fósforo (P), el alto contenido de hierro (Fe) y de aluminio (Al) intercambiable, limitan el buen desarrollo (Armijos, 2013; Molina-Quesada et al., 2018).

La productividad de una especie en un sitio se mide a través del índice de sitio (IS), que está asociado a variables climáticas y edáficas que condicionan su crecimiento y rendimiento. Para definir el IS, en general, se utilizan indicadores intrínsecos al rodal, siendo la altura dominante la más apropiada debido a su baja dependencia de la densidad, de los tratamientos silviculturales y a la alta correlación con la producción (Alder, 1980; Dantani et al., 2019; Michone et al., 2017).

Diversos autores apuntan que el rendimiento de una plantación es afectado por la calidad de sitio (Armijos, 2013; Bermejo et al., 2004; Camacho-Linton et al., 2013; Nunifu y Murchison, 1999), de ahí la importancia de su determinación para predecir con la mayor confiabilidad posible la futura producción del sistema establecido.

Es esencial cuantificar y predecir con certeza el volumen de madera, de esta forma, se facilita la gestión de los proyectos forestales. Por lo anterior, las personas productoras necesitan de herramientas prácticas, generadas a partir de variables de fácil medición en campo, para calcular el volumen de madera, de forma sencilla y precisa (Armijos, 2013; Tewari y Singh, 2018); y que les beneficie en sus transacciones de compra o venta (Sulastri, 2015).

El volumen de un árbol se puede obtener a partir del diámetro a la altura del pecho (DAP, medición que corresponde a 1.3 m desde la base del árbol) y la altura, ambas variables medidas durante las actividades de inventario (Armijos, 2013; Sianturi, 2015; Sulastri 2015). Por otra parte, mediante modelos matemáticos, se pueden generar ecuaciones de predicción de volumen que logren el mismo fin (Akindele, 1991; Ureigho y Akpobome, 2018), generados a partir de ambas variables predictoras.

Distintas investigaciones han ajustado funciones matemáticas para estimar la producción en volumen de teca (Armijos, 2013; Drescher et al., 2014; Cerqueira et al., 2017; Telles et al., 2018; Tewari y Singh, 2018; Ureigho y Akpobome, 2018) y para Costa Rica (Bermejo et al., 2004; Camacho y Madrigal, 1997; Fallas, 2017; Gómez y Mora, 2003; Pérez y Kaninnen, 2007).

Las ecuaciones o modelos matemáticos son la base para desarrollar tablas de volumen de madera de un árbol, a partir de su altura o diámetro (Armijos, 2013; Camacho et al., 2013; Sianturi, 2015; Sulastri, 2015; Tamarit et al., 2013). Resulta esencial cuantificar y predecir con certeza el volumen de madera, de esta forma, se facilita la gestión de los proyectos forestales.

Tanto técnicos como productores requieren herramientas prácticas, generadas a partir de variables de fácil medición en campo, para calcular el volumen de madera de forma sencilla y precisa (Armijos, 2013; Tewari y Singh, 2018); y que les beneficie en sus transacciones de compra y/o venta (Sulastri, 2015).

Es por todo lo anterior que, el objetivo de este trabajo fue elaborar tablas de volumen comercial con corteza, de una sola entrada (DAP), por clase diamétrica, a partir del ajuste y la selección de ecuaciones matemáticas para teca clonal de 10 años, en diferentes índices de sitio, en la zona norte de Costa Rica. Se espera con este producto, contribuir en la adecuada gestión de los sitios forestales y la planificación de su rendimiento.

2. Metodología

2.1 Área de estudio

El estudio se realizó en el año 2016, en plantaciones clonales de T. grandis de 10 años en una finca privada de más de 70 ha, localizada en el distrito Pocosol, cantón San Carlos, provincia Alajuela, en la zona norte de Costa Rica. Las cuales están ubicadas alrededor de las coordenadas geográficas 10°49´34,607” N y 84°25´45.287” W, donde se registra una altitud promedio de 100 m s.n.m (Figura 1).

La zona presenta un clima lluvioso, con un promedio anual de precipitación de 3 020 mm y una temperatura media de 26 °C. La topografía es moderadamente ondulada con pendientes de 15 y 30 %. Mayoritariamente, los suelos son Ultisoles, por lo general profundos y bien drenados, color rojo o amarillo y de baja fertilidad (Solano y Villalobos, 2000).

Dicha finca fue plantada y manejada de manera homogénea. La preparación del terreno incluyó rastra, así como enmiendas al suelo y control de arvenses en forma de rodajas de 1 m de diámetro alrededor de cada árbol; adicionalmente, se le realizaron 2 raleos a la masa. El material clonal fue establecido en campo de forma aleatoria por la empresa, donde se utilizaron no más de 20 genotipos.

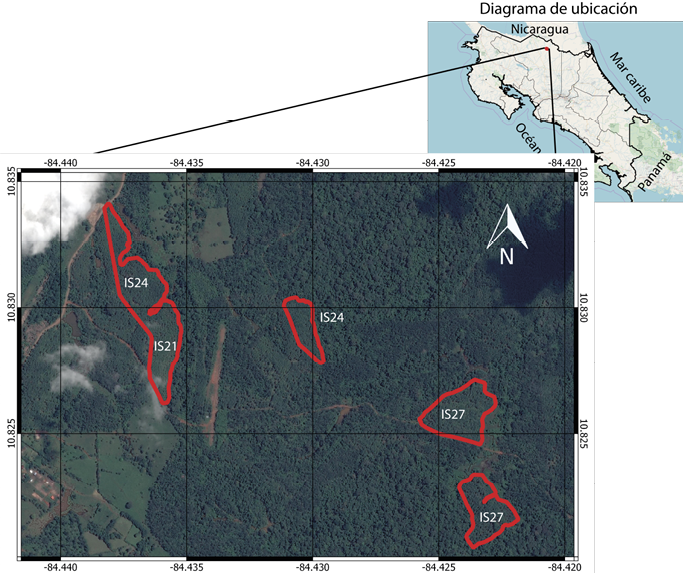
Figura 1. Ubicación de las plantaciones de teca evaluadas, Pocosol, San Carlos, Costa Rica.
Figure 1. Location of the teak plantations evaluated, Pocosol, San Carlos, Costa Rica.

2.2 Determinación del índice de sitio (IS)

La empresa propietaria de las plantaciones aportó la base de datos con información dasométrica, obtenida por medio de la medición de parcelas permanentes de monitoreo (PPM). De estas se determinó la altura dominante como el promedio de la altura total (H) del 10 % de los árboles más gruesos y más altos de cada unidad de muestreo. Para ello, se eligieron árboles utilizando tanto el DAP como la altura total, y con ambos crear un índice que identificara los más gruesos y más altos.

Se le dio un peso en la ponderación de 30 % al DAP y 70 % a la altura, de esta forma se evitó utilizar árboles que fueran gruesos pero bajos o altos pero delgados. Para utilizar el índice creado, se reordenaron los árboles de mayor a menor, con base en la altura total, luego se promedió la altura de los árboles que representan el 10 %. El índice de sitio se determinó al contrastar la altura dominante obtenida para cada lote con las curvas de índice de sitio desarrolladas por Mora y Meza (2003) para Costa Rica a una edad base de 16 años.

2.3 Selección de árboles para calcular el volumen

Inicialmente, se seleccionaron en forma aleatoria 2 parcelas para cada IS; sin embargo, en campo se decidió eliminar una parcela del IS21 debido a la poca homogeneidad del lote donde se ubicaba. Se determinó en oficina la cantidad de árboles en una distribución diamétrica de 3 cm para cada PPM. Se localizó en campo las PPM para marcar y cortar los árboles de la muestra. En total se cortaron 266 árboles (119 para IS27, 119 para el IS24 y 28 para el IS21).

Antes de derribar cada árbol, se midió su DAP y se hizo una marca en el fuste a esta altura; posteriormente, se midió el diámetro (cm) a la base (a 10 cm del suelo), y a partir de este punto, cada 1.5 m hasta el ápice. Además, se midió la altura comercial en metros (HC) hasta un diámetro mínimo de 15 cm con corteza (Figura 2).

2.4 Procesamiento de los datos

Se creó una base de datos, para realizar el cálculo del volumen de cada segmento del árbol, obtenido mediante la fórmula de Smalian (Ecuación 1). El volumen comercial fue la suma del volumen parcial de cada segmento hasta la altura comercial, según se muestra en la Ecuación 1.

Vm3: 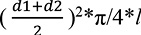(E. 1)

Donde:

Vm3 = volumen del segmento en metros cúbicos.

l = longitud del segmento en metros.

d1= diámetro con corteza en el extremo mayor de la troza, en metros.

d2= diámetro con corteza en el extremo menor de la troza, en metros.

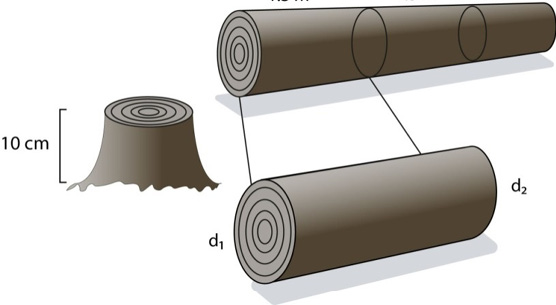
Figura 2. Cubicación de las trozas.
Figure 2. Logs cubing.

2.5 Desarrollo, selección y comparación de modelos

Los modelos se ajustaron mediante el método de mínimos cuadrados ordinarios con el programa Statgrapihcs Centurion XVI, y se empleó como variable independiente el diámetro (DAP). Para cada índice de sitio se probaron los siguientes 10 posibles modelos: Raíz Cuadrada Doble, Raíz Cuadrada-Y Log-X, Cuadrado de X, Raíz Cuadrada-Y Inversa de X, Lineal, Raíz Cuadrada de X, Logaritmo de X, Curva S, Raíz Cuadrada de Y y el Multiplicativo.

A cada uno de los modelos, se les calculó los siguientes estadísticos: coeficiente de determinación (R2), error estándar de la estimación (EEE), error medio absoluto (EMA), tamaño de la muestra (n), error del modelo o sesgo (E %), error cuadrático medio (ECM), la diferencia agregada (DA) y la suma de cuadrados de los residuos de los valores predichos (PRESS). Adicionalmente, se calculó el criterio de información de Akaike (AIC); para comparar los modelos con trasformación de la variable dependiente se utilizó el Índice de Furnival (IF) y para comprobar la autocorrelación de los residuos se utilizó la prueba de Durbin-Watson (DW).

Para evaluar los modelos y seleccionar el de mejor ajuste, los estadísticos citados arriba se normalizaron convirtiéndolos a una escala común para compararlos. La escala utilizada fue de 0 a 1, donde 0 es el valor menos deseable y 1 el más deseable. En los casos en que la variable tiene un sentido inverso de valor (relación negativa) todas las medidas de error son representadas por valores absolutos o relativos, cuyo mejor valor es aquel que se acerque a cero, por lo tanto, en ellos se invirtió el sentido del valor de la variable para que las medidas de los errores queden normalizadas de 0 a 1 (relación directa positiva), pero representando el mejor valor por la cercanía a uno (Ecuación 2).

Ʃvn= (R2vn) + (EEEvn)+ (EMAvn)+ (DWvn)+ (nvn)+ (ECMvn)+
(DAvn)+ (IFvn)+ (PRESSvn)+ (E%vn) + (AICvn) (E. 2)

Donde:

Ʃvn= sumatoria de valores normalizados de 0 a 1, R2vn= coeficiente de determinación, EEEvn= error estándar de la estimación, EMAvn= error absoluto medio, DWvn= prueba de Durwin Waston, nvn= tamaño de la muestra, ECMvn= error cuadrático medio, DAvn= diferencia agregada, IFvn= Índice de Furnival, PRESSvn= sumatoria de los residuos al cuadrado, E%vn= error relativo, AICvn= criterio de Información de Akaike.

Se utilizaron las ecuaciones para normalizar los siguientes estadísticos:

•1-Eec*1/Emax, para EEE, EMA, ECM, PRESS, E%, DA e IF

•La prueba de Durbin-1*DWec/4), para DW

•1*AICec/AICmin, para AIC

Donde: Eec =Valor del error de la ecuación, Emax: Valor del error máximo de todas las ecuaciones, DWec =Valor de DW de la ecuación, AICec =Valor AIC de la ecuación, AICmin: Valor mínimo del AIC de todas las ecuaciones. VCcc: Volumen comercial con corteza.

El modelo con el valor más alto en la sumatoria de los estadísticos normalizados resultó elegido; después, se analizaron los residuos (Vobservado –Vpredicho) en función de la variable dependiente. El modelo seleccionado para cada índice de sitio se comparó con los modelos de predicción de volumen para T. grandis en Costa Rica generados por Fallas (2017) y Pérez y Kanninen (2007). Finalmente, a partir de la ecuación seleccionada se generó la tabla de volumen comercial con corteza.

3. Resultados

3.1 Índices de sitio

Según los datos de PPM de la empresa, las plantaciones evaluadas se clasifican en 3 índices de sitio, el mayor (IS27) con una altura dominante de 22.2 m, 19.5 m para el IS24 y 15.5 m en el IS21. La condición dasométrica (DAP, altura y volumen) de las plantaciones disminuyó con la calidad de sitio, con diferencias en diámetro de más de 8 cm (39 % aproximadamente) para el árbol promedio entre el IS27 y el IS21. En volumen la diferencia fue de 0.2519 m3 (90 % aproximadamente) entre los mismos índices. A pesar de ser plantaciones clonales, se observa un amplio rango diamétrico de 19.3; 19.0 y 10.1 cm para el IS27, 24 y 21, respectivamente (Cuadro 1).

Cuadro 1. Estadísticos de las variables evaluadas en árboles de T. grandis por IS
Table 1. Statistics of the variables evaluated in T. grandis trees by IS.

Estadísticos	Índice de sitio 27			Índice de sitio 24			Índice de sitio 21
	DAP	Vol c	HC	DAP	Vol c	HC	DAP	Vol c	HC
n	119	119	119	119	119	113	28	28	28
X	22.8	0.2854	8.35	17.6	0.1054	4.04	13.9	0.0305	1.56
SD	4.34	0.15	3.23	3.45	0.08	2.53	2.41	0.03	1.16
CV	19.1	53.5	38.7	19.6	78.6	62.5	17.3	101.0	74.5
Mínimo	13.8	0.0200	1.00	9.0	0.0000	0.10	9.0	0.0000	0.30
Máximo	33.1	0.6524	15.30	28.0	0.3970	9.75	19.1	0.1180	4.50

n: tamaño de la muestra, X: promedio SD: desviación estándar, CV: coeficiente de variación (%), DAP (cm), Vol c: volumen comercial (m3*árb-1), HC: Altura comercial (m).

3.2 Modelos para estimar volumen por índice de sitio

Los modelos elegidos “Raíz Cuadrada-Y Log-X” para los IS27 y 24 y “Raíz cuadrada doble” para el IS21, presentaron un ajuste muy aceptable con R2 > 0.94 y errores de estimación (E %) inferiores al 3 %. El valor de la prueba de DW para los índices 24 y 21 sugiere que no existe autocorrelación de los residuos, ya que los resultados estuvieron muy cercanos a 2, mientras que para el IS27 el valor de “P” es menor que 0,05, indicación de una posible correlación serial. Los otros estadísticos también muestran cifras muy bajas, que demuestran excelente capacidad predictora y precisión (Cuadro 2).

Cuadro 2. Modelos seleccionados para la estimación de volumen comercial con corteza. Todos los modelos poseen una P < 0.001.
Table 2. Selected models for estimating commercial volume with bark. All models have a P < 0.001.

Índice de sitio	Modelo seleccionado	R2	EEE	EMA	DW	ECM	DA	IF	PRESS	E%	AIC
IS27	Vccc = (1.65557 + 0.763516*ln(DAP))2	0.94	0.037	0.029	1.41(P=0.0006)	0.038	0.0013	0.025	0.173	2.3	-3.1
IS24	Vccc = (1.49438 + 0.685618*ln(DAP))2	0.94	0.036	0.027	1.92(P=0.3380)	0.024	0.0014	0.0146	0.069	3	-3.52
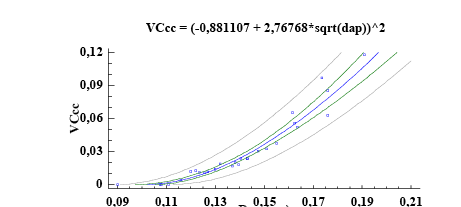
IS21	Vccc = (-0,881107 +2,76768*sqrt(DAP))2	0.94	0.022	0.017	2.07(P=0.5198)	0.007	0.0000	0.022	0.001	-1.4	-3.73

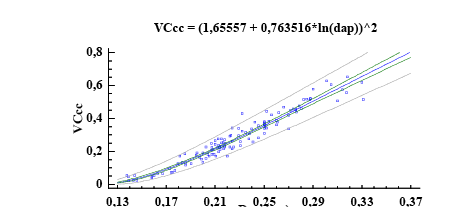
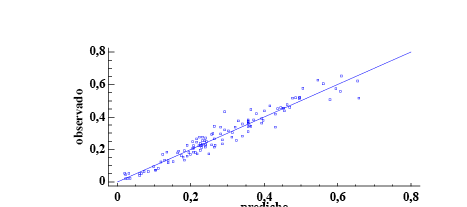
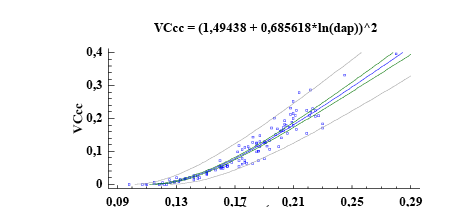
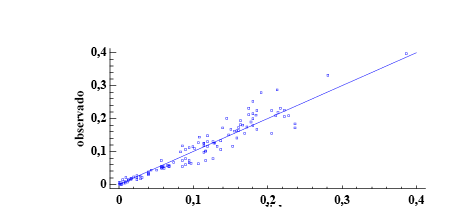
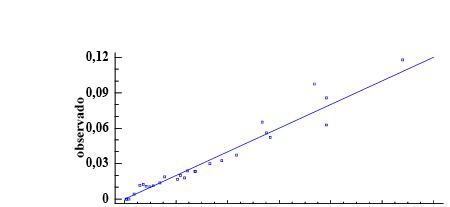
La forma de la curva que resultó de la relación entre el DAP y el volumen comercial se observa en la Figura 3a, el modelo ajustado lo representa la línea central, las siguientes 2 indican el intervalo de predicción y las líneas externas el intervalo de confianza. La Figura 3b muestra la distribución de residuos del volumen comercial con corteza. En los 3 modelos la distribución es homogénea sobre la línea de tendencia central, lo que indica que no se viola el supuesto de normalidad en la distribución residual.

a (IS 27)	b (IS 27)
a (IS 24)	b (IS 24)
a (IS 21)	b (IS 21)

Figura 3. Modelos para los IS27, 24 y 21: a) gráfico para el modelo ajustado b) gráfico de los valores predichos vs observados.
Figure 3. Models for IS27, 24 and 21: a) graph for the adjusted model b) graph of predicted vs. observed values.

3.3 Comparación de los modelos entre IS

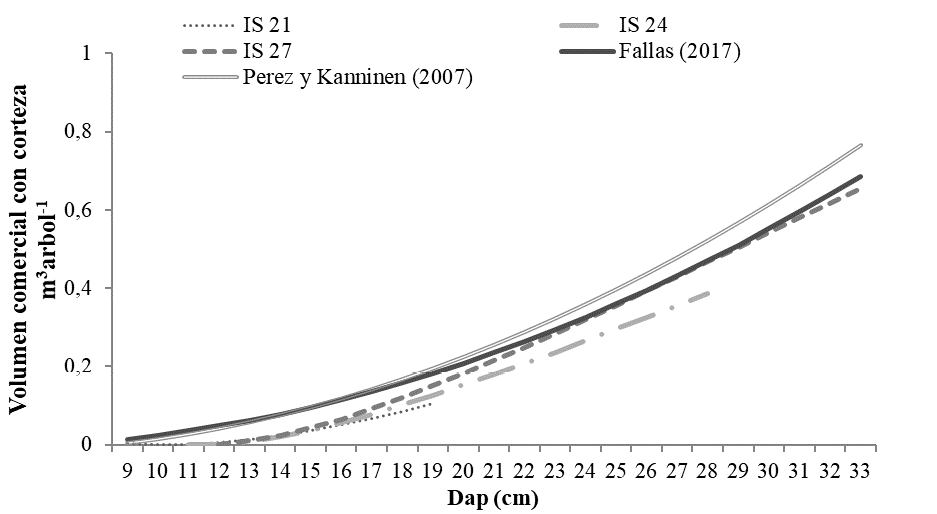
En árboles con DAP inferior a 16 cm, los 3 modelos registraron un comportamiento muy similar, arrojando cifras en volumen prácticamente iguales; sin embargo, a partir de los 16 cm, se observan diferencias, con una superioridad marcada del modelo para el índice de sitio 27 (Figura 4).

Figura 4. Comparación del modelo ajustado para volumen comercial con corteza de teca con otros modelos para volumen comercial en Costa Rica.
Figure 4. Comparison of the adjusted model for commercial volume with teak bark with other models for commercial volume in Costa Rica.

El volumen comercial con corteza obtenido con el modelo elegido para cada IS, se comparó con el predicho con otros modelos reportados en la literatura. Se observa en la Figura 4 que los modelos generados por Fallas (2017) y Pérez y Kanninen (2007) tienen una curva muy similar al modelo del IS27 obtenido en la presente investigación; lo que brinda una idea de los sitios estudiados por dichos autores. Por su parte, los modelos de los índices de sitio 24 y 21 predicen valores inferiores a los obtenidos por Fallas (2017) y Pérez y Kanninen (2007) (Figura 4).

3.4. Tabla de volumen

El volumen comercial con corteza para árboles de teca se presenta en el Cuadro 3. Esta es la herramienta de uso práctico, por medio de la cual es posible obtener el volumen (actual o futuro) del árbol con solo tener información del diámetro; puede ser aplicada para materiales genéticos con un desempeño similar a los aquí estudiados. La tabla de volumen incluye diámetros desde 15 hasta 33 cm.

Cuadro 3. Tabla de volumen comercial con corteza (m3 arbol-1) para teca clonal de 10 años para los índices de sitio 27, 24 y 21; en zona norte, Costa Rica.
Table 3. Commercial volume table with bark (m3 tree-1) for ten-year clonal teak for site index 27, 24 and 21; in north zone, Costa Rica.

DAP (cm)	IS27		IS24	IS21
15	0.0429		0.0375	0.0364
16	0.0657		0.0566	0.0511
17	0.0916		0.0781	0.0676
18	0.1199		0.1016	0.0859
19	0.1502		0.1266	0.1058
20	0.1821		0.1528
21	0.2153		0.1801
22	0.2495		0.2082
23	0.2846		0.2369
24	0.3203		0.2662
25	0.3565		0.2958
26	0.3932		0.3258
27	0.4302		0.3560
28	0.4674		0.3864
29	0.5047
30	0.5422
31	0.5797
32	0.6172
33	0.6546

IS27: Índice de sitio 27, IS24: Índice de sitio 24, IS21: Índice de sitio 21.

4. Discusión

4.1. Índice de sitio

Para este estudio, se identificó con mayor productividad el IS27; donde la altura dominante de 22.2 m coincide con la mejor calidad de sitio calculada por Vaides et al., (2004) en Guatemala y Drescher et al. (2014) en Brasil. Ambos determinaron como clase de productividad alta desde 20 m hasta 24 m en altura dominante a los 10 años, mientras fue superior a las mejores clases de sitio en Ghana a los 10 años con 15 m (Nunifu y Murchinson, 1999).

En el IS24 la altura de 19.5 m está dentro del rango determinado por Vaides et al. (2004) en Guatemala para sitios promedio (16-20 m) a los 10 años, mientras Bermejo et al. (2004) reportaron 20.7 m para sitios promedio a la misma edad. En el índice de sitio 21, la altura (15.5 m) es superior a lo reportado por Corona et al., (1999) en Cuba y Nunifu y Murchinson (1999) en Ghana; en estas investigaciones, para la mejor calidad de sitio, se registró 6.9 m y 14.6 m de altura a los 10 y 12 años, respectivamente.

La significativa diferencia registrada entre el IS21 y el IS27 sugiere que el primero no es ideal para desarrollar plantaciones comerciales, debido a que el volumen comercial será muy bajo. Según Vaides et al. (2004), una altura menor a 16 m representa un sitio bajo en productividad; la que, podría estar vinculada a diversos aspectos que van desde el material genético, pasando por factores limitantes propios del sitio que no fueron corregidos, hasta un manejo inadecuado de la masa.

El promedio en diámetro para el IS27 es superior a lo reportado en algunas investigaciones, incluso para edades superiores, tal es el caso de Camacho et al. (2013) en México con 20.7 cm a 11 años, mientras que Fallas (2017) calculó para plantaciones clonales menores a 12 años desde 8.6 a 32 cm, con mayor concentración de individuos en el rango de 10 a 15 cm; Bermejo et al. (2004) reportaron 10 a 21.8 cm para plantaciones de 11 años en Costa Rica.

El diámetro promedio para el IS24 (17.6 cm) es similar al indicado por Telles et al. (2018) (16.55 cm en México a 11 años); Nunifu y Murchison (1999) en sitios buenos en Ghana (clase 1 según Nunifu y Murchinson 1999) reportaron 16.3 cm; mientras que, para Costa Rica, Bermejo et al. (2004) determinaron un DAP promedio de 17.6 cm a la edad de 11 años. El IS21 presenta un DAP promedio de 14.56 cm, similar a lo que encontraron Cerqueira et al. (2017), un DAP promedio de 13.2 cm y un promedio de altura total de 10.2 m a los 10 años en Brasil.

La variabilidad observada en el volumen comercial, entre los índices de sitio para las mismas clases diamétricas, pese a que fueron manejados de la misma forma y utilizando el mismo material genético, es producto de las diferencias en diámetro y altura comercial, que pueden ser consecuencia de la calidad del sitio (productividad del sitio) (Camacho et al., 2013; Corona et al., 1999; Bermejo et al., 2004; Nunifu y Murchison 1999), recalcando la necesidad de clasificar los sitios para estimar su productividad potencial, por lo que se considera que este estudio es de utilidad en la predicción realista del volumen, cortas intermedias y cosecha final.

4.2. Modelos para estimar volumen por índice de sitio

El índice de sitio 27 registró el mayor volumen comercial promedio (0.28 m3*árbol-1), valor similar al obtenido por Fallas (2017) con 0.30 m3*árbol-1 para plantaciones de material clonal de menos de 12 años, y al indicado por Camacho et al. (2013) (0.269 m3*árbol-1) para sitios de nivel medio con 9 años en México, mientras que Drescher et al. (2014) en Brasil, reportaron un volumen total de 0.3129 m3*árbol-1 a los 10 años. Sin embargo, es inferior a lo reportado por Armijos (2013), quien determinó 0.41 m3*árbol-1 de volumen comercial a los 13 años en Ecuador.

En el índice de sitio 24, el promedio fue de 0.1054 m3*árbol-1, en el mismo diámetro y altura total Drescher et al. (2014) reportaron 0.1570 m3*árbol-1 para volumen total, lo que sugiere el uso de un factor mórfico diferente entre estudios. Una cifra igual a la obtenida en el presente estudio reportó Corona et al. (1999), para plantaciones en Cuba en calidad de sitio 2, con una altura dominante de 8.10 m a la edad de 10 años. En el índice de sitio 21 el volumen fue de 0.0356 m3*árbol-1, menor a lo reportado por Camacho et al. (2013) para sitios de nivel bajo en México (0.0685 m3*árbol-1, volumen total del fuste con corteza a los 10 años). El volumen comercial es en parte indicación de la influencia de la calidad del sitio.

El proceso de selección de los modelos depende, en primer lugar, de la representatividad de la información usada en su construcción y, adicionalmente, de la rigurosidad en la selección del mejor modelo, lo que garantiza que la ecuación escogida sea la más adecuada para los datos, ya que los valores coincidirán con los parámetros estadísticos calculados.

En el presente estudio se contó con una base de datos de 119 observaciones para los IS27 y 24 y de 28 para el IS21 y se calcularon 11 parámetros estadísticos, por lo que los modelos seleccionados se pueden utilizar con confiabilidad. Al respecto, autores como Telles (2018), Tamarit et al. (2013), Tewari et al. (2013) y Tewari y Singh (2018) recomiendan utilizar el criterio de selección expuesto por Sakici et al. (2008), que consiste en jerarquizar los estadísticos de mayor a menor calificación.

Los resultados para la prueba de Durbin-Watson con valores cercanos a 2 demuestran que no violan los supuestos de regresión, al no determinar autocorrelación de los residuos. Con el criterio de información de Akaike (AIC), según Tewari y Singh (2018), valores menores a 2 deben ser considerados para el ajuste del modelo, seleccionando como mejor aquel con el menor valor.

En este estudio se obtuvo para todos los modelos valores inferiores a 2, este criterio de selección también fue considerado por Tamarit et al. (2013). La distribución de los residuos sobre la línea central indica que no se violó el supuesto de normalidad, coincidente con los hallazgos de Telles (2018), Fallas (2017), Cerqueira et al. (2017), Drescher et al. (2014); Ureigho y Akpobome (2018); Nurudeen et al. (2014).

Por lo general, en la mayoría de los estudios de esta naturaleza, la selección de ecuaciones se basa en parámetros como el R2, error estándar de la medición, desviación estándar. Al respecto, Pérez y Kanninen (2007) se basaron en el R2 para escoger un modelo que predice el volumen total con base en el DAP y la altura total. Por su parte, Moret et al. (1998), Camacho y Madrigal (1997), Sulastri (2015), Sianturi (2015) y Telles (2018) utilizaron entre 3 y 5 parámetros para realizar la escogencia de las ecuaciones; mientras que, Bermejo et al. (2004) y Tamarit et al. (2013) utilizaron 6 y 7 parámetros, respectivamente, para el mismo fin.

De la misma manera que en el presente estudio, Moret et al. (1998) y Pérez y Kanninen (2007) incluyeron el índice de Furnival (IF) para la selección del modelo; adicionalmente, la prueba de Durbin-Watson fue utilizada por Telles (2017) y Tamarit et al. (2013); mientras que el criterio de información de Akaike (AIC) fue considerado como criterio de selección en los trabajos de Tewari y Singh (2018); Tewari (2013) y Tamarit et al. (2013). Lo anterior apunta que la rigurosidad que se debe presentar en la selección del mejor modelo está condicionada a maximizarse con base en un número creciente de parámetros estadísticos; razón por la cual se utilizaron 11 de ellos.

El buen ajuste exhibido por los modelos seleccionados en este trabajo (R2 ≥ 94 %) y (E % < 3 %), para los 3 índices de sitio muestran mucha confiabilidad, además de la facilidad en su aplicación por utilizar solo una variable predictora. Condición similar fue reportada por Tewari y Singh (2018) en la India quienes obtuvieron R2 de 97.7 %; Fallas (2017) obtuvo un R2 de 98 % y errores de estimación bajos (< 2 %) para material clonal en plantaciones de menos de 12 años en Costa Rica. Este último autor señala que la silvicultura clonal genera crecimientos más homogéneos en los árboles y las plantaciones, que proporciona facilidades en el ajuste de modelos matemáticos con mayor precisión.

4.3. Comparación de modelos

La forma de la curva del modelo elegido para el IS27 presenta una tendencia muy similar al escogido por Pérez y Kanninen (2007) y prácticamente, igual al modelo de Fallas (2017); dicha semejanza puede ser explicada por utilizar material clonal con cierto nivel de selección genética (Figura 4). Ambos autores ajustaron modelos con datos de árboles de 2 a 47 años y con un diámetro mínimo comercial de 10 cm.

Los modelos para los 3 índices de sitio mantienen una tendencia muy similar en las primeras clases diamétricas. A partir de un DAP de 16 cm se muestra la superioridad del IS27, y los IS24 y 21 reportan menor DAP y volumen. Lo anterior resulta esperable, por los factores intrínsecos a dichos sitios que provocan una menor productividad.

El hecho que la masa fuera silviculturalmente manejada de la misma forma y haberse utilizado igual material genético, indica que la variabilidad observada en el volumen comercial entre los índices de sitio para las mismas clases diamétricas es producto de diferencias en la altura comercial registrada. Diversos autores concluyen que, lo anterior, es consecuencia de diferencias en la calidad entre sitios, lo que se vincula directamente con su productividad (Nunifu y Murchison 1999; Corona et al. 1999; Bermejo et al. 2004; Camacho et al. 2013). Con esto se ratifica la importancia de clasificar de previo los sitios, para, con ello, obtener un estimado más preciso de la productividad potencial de la totalidad de la finca.

4.4. Tabla de volumen

La tabla de volumen construida presenta la ventaja de requerir únicamente el DAP del árbol, sin necesidad de medir la altura, lo cual representa un proceso lento y muchas veces poco exacto (Armijos, 2013). A pesar de su utilidad, se debe tener cuidado que al utilizar esta herramienta se considere la calidad del sitio y el material genético evaluado.

Autores como Corona et al. (1999), Torres Del Valle et al. (2012), Akindele 1991 y Minoche et al., (2017) apuntan que mediante el índice de sitio es posible clasificar la productividad, lo que permite una estimación más precisa del volumen esperable, y con ello optimizar la planificación y la prescripción de actividades para un deseado manejo silvicultural de la masa.

5. Conclusiones

Las plantaciones evaluadas corresponden a los IS 27, IS 24 e IS 21, este último no es recomendable para el establecimiento de masas comerciales por su baja productividad.

Los modelos elegidos para estimar el volumen comercial en los 3 índices de sitio presentaron una bondad de ajuste muy buena (R2 > 0.94), con bajos errores de estimación. Asimismo, muestran la ventaja de la simplicidad en su uso, por utilizar como variable predictora, el diámetro a la altura del pecho (DAP). Los resultados ratifican confiabilidad del DAP como variable predictora, en la estimación del volumen comercial del árbol individual, mediante la generación de ecuaciones de regresión.

Los modelos ajustados representan una importante herramienta para cuantificar el volumen comercial con corteza de teca clonal desde 15 cm de diámetro, para plantaciones con características similares a las del presente estudio. Por tanto, se recomienda ser cauteloso al intentar aplicarlos en condiciones distintas a las evaluadas.

6. Ética y conflicto de interés

Las personas autoras declaran que han cumplido totalmente con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en la producción del manuscrito; que no hay conflictos de intereses de ningún tipo; que todas las fuentes financieras se mencionan completa y claramente en la sección de agradecimientos, y que están totalmente de acuerdo con la versión final editada del artículo.

7. Agradecimientos

Los autores expresan su agradecimiento al proyecto “Evaluación del crecimiento de plantaciones clonadas de teca y melina y determinación de la rentabilidad de la producción de madera de ambas especies” desarrollado en el Instituto de Investigación y Servicios Forestales de la Universidad Nacional (INISEFOR-UNA), por su apoyo en la logística y el financiamiento de la presente investigación. A la Empresa Proteak S. A., por facilitar el acceso a sus fincas para la recolección de información. A los estudiantes de ingeniería forestal que voluntariamente colaboraron en la recolección de los datos durante el trabajo de campo y a las personas revisoras anónimas de la revista por sus aportes, los cuales enriquecieron el manuscrito.

8. Referencias

Akindele, S. O. (1991). Development of a site index equation for teak plantations in Southwestern Nigeria. Journal of Tropical Forest Science, 4(2), 162-169. https://www.jstor.org/stable/43596244

Alder, D. (1980). Estimación del volumen forestal y predicción del rendimiento, con referencia especial a los trópicos. Organización de las Naciones Unidas para la Agricultura y la Alimentación, Roma, Italia.

Armijos, D. (2013). Construcción de tablas volumétricas y cálculo de factor de forma (ff.) para dos especies, teca (Tectona grandis) y melina (Gmelina arborea) en tres plantaciones de la empresa Reybanpac ca. en la provincia de los Ríos. (Tesis de grado). Escuela Superior Politécnica de Chimborazo. Riobamba, Ecuador.

Badilla, Y. y Murillo, O. (2017). Ganancia realizada en plantaciones clonales de teca en Costa Rica. En: I Simposio Internacional GENFORES. 26-27 enero, 2017. Instituto Tecnológico de Costa Rica. Cartago, Costa Rica.

Bermejo, I., Cañellas, I. y San Miguel, A. (2004). Growth and yield models for teak plantations in Costa Rica. Forest Ecology and Management, (189), 97-110. https://doi.org/10.1016/j.foreco.2003.07.031

Camacho-Linton, A., Ramírez-Maldonado, H., de los Santos-Posadas, H. M. y Zamudio-Sánchez, F. J. (2013). Tablas de rendimiento para teca (Tectona grandis L.) en el Estado de Campeche. Revista Mexicana de Ciencias Forestales, 4(19), 92–101. https://doi.org/10.29298/rmcf.v4i19.381

Camacho, P. y Madrigal, T. (1997). Ecuaciones de volumen preliminares para Tectona grandis. En 3. Congreso Forestal Nacional. 27-29 agosto 1997. No. 634.9097286063 C749 1997. (pp. 131–133). San José, Costa Rica.

Cerqueira, C., Dos Santos, G., De Jesús, L., Mora, R., Marques, G., Salles, T. y Brianezi, D. (2017). Modelagem da altura e volume de Tectona grandis L. F. na mesorregião Nordeste do Pará. Nativa: Pesquisas Agrárias e Ambientais, 5(Especial), 606-611. https://doi.org/10.5935/2318-7670.V05nespa22

Corona, I., Jacas, F., Tamayo, F., y Pereira, A. (1999). Índice de sitio y tablas de crecimiento para plantaciones jóvenes de Tectona grandis L. en la Unidad silvícola Guisa, Cuba.

Dantani, A., Shamaki, S., Gupa, M., Sa’idu, M., Mukhtar, R., Umar, M. y Abubakar, A. (2019). Allometric Models for Estimating Site Index of Teak (Tectona grandis Linn F.) in Kanya Forest Plantation, Kebbi State, Nigeria. Asian Journal of Environment y Ecology, 10(1), 1-7. https://doi.org/10.9734/ajee/2019/v10i130110

Drescher, R., Gava, F. H., Pelissari, A. L., Acosta, F. C. y Silva, V. (2014). Equações volumétricas para Tectona grandis Linn F. em povoamentos jovens no estado de Mato Grosso. Advances in Forestry Science, Cuiabá, 1(2), 65-70.

Fallas, J. (2017). Funciones alométricas, de volumen y de crecimiento para clones de teca (Tectona grandis L. F.) en Costa Rica. (Tesis de maestría). Instituto Tecnológico de Costa Rica, Cartago, Costa Rica.

Gómez, M. y Mora, F. (2003). Comparación de modelos y unificación de ecuaciones de volumen para árboles individuales en plantaciones de teca (Tectona grandis Linn) en Costa Rica. En Plantaciones de teca (Tectona grandis): posibilidades y perspectivas para su desarrollo. Seminario y Grupo de Discusión Virtual. (Disco compacto), 26 al 28 de noviembre de 2003, Heredia, Costa Rica, 16 p.

Instituto Nacional de Estadística y Censos [INEC]. (2015). VI Censo Nacional Agropecuario: Resultados Generales. Instituto Nacional de Estadística y Censos. 1 ed. San José, Costa Rica.

Ladrach, W. (2009). Manejo de plantaciones de la teca para productos sólidos, ISTF, (Sociedad Internacional de Forestales Tropicales). http://www.istf-bethesda.org/specialreports/teca_teak/teca.pdf

Madeiros, R., Nogueira, H., Siqueira, F. & Garcia, H. (2018). Growth and yield of teak stands at different spacing. Pesquisa Agropecuária Brasileira, 53(10):1109-1118. https://doi.org/10.1590/s0100-204x2018001000004

Minoche, D. Herrero C., Domínguez M. y Martínez. P. (2017). Determinación del índice de sitio de las plantaciones de teca (Tectona grandis L.) en Tabasco, México. Ciencia e Investigación Agraria, 44(2), 154-167. http://rcia.uc.cl/index.php/ijanr/article/view/1645

Molina-Quesada, S., Alfaro, C., Murillo, O., Badilla, Y. y Luján, R. (2018). Evaluación del comportamiento de clones de Tectona grandis L. F. en suelos vertisoles de la Península de Nicoya, Costa Rica. Revista Forestal Mesoamericana Kurú, 16(38), 24-34. https://doi.org/10.18845/rfmk.v16i38.3993

Mora, F. y Hernández, W. (2007). Estimación del volumen comercial por producto para rodales de teca en el Pacífico de Costa Rica. Agronomía Costarricense, 31(1), 101-112. https://www.mag.go.cr/rev_agr/v31n01_101.pdf

Mora, F. y Meza, V. (2003). Curvas de índice de sitio para teca (Tectona grandis Linn.) en la vertiente del Pacífico de Costa Rica. En Plantaciones de Teca (Tectona grandis): posibilidades y perspectivas para su desarrollo. Seminario y Grupo de Discusión Virtual. (Disco compacto), 26 al 28 de noviembre de 2003, Heredia, Costa Rica.

Moret, A. Y., Jerez, M., y Mora, A. (1998). Determinación de ecuaciones de volumen para plantaciones de teca (Tectona grandis L.) en la Unidad Experimental de la Reserva Forestal Caparo, Estado Barinas–Venezuela. Revista Forestal Venezolana, 42(1), 41-50. http://www.saber.ula.ve/handle/123456789/24242

Nunifu, K. y Murchison, H. (1999). Provisional yield models of teak (Tectona grandis L. F.) plantations in northern Ghana. Forest Ecology and management, 120(1-3), 171-178. https://doi.org/10.1016/S0378-1127(98)00529-5

Nurudeen, T., Abiola, J., Salami, K., Erinle, O. y Olaniyi, W. (2014). Regression Models for Tree Volume Prediction in Stands of Tectona grandis Linn at Federal College of Forestry, Jericho, Ibadan, Oyo State Nigeria. Science Journal of Agricultural Research and Management, 2014. https://doi.org/10.7237/sjarm/233

Pérez, L. y Kanninen, M. (2007). Estimación del volumen comercial a diámetros y alturas variables para Tectona grandis L. F. en Costa Rica. Recursos Naturales y Ambiente, (49-50).

Sakici, O., Misir, N., Yavuz, H. y Misir, M. (2008). Stem taper functions for Abies nordmannia subsp. bornmulleriana in Turkey. Scandinavian. Journal of Forest Reserch, 23(6), 522-533. https://doi.org/10.1080/02827580802552453

Sianturi, A. (2015). Development of the local volume table wood carpentery of jati (Tectona grandis L. F.) in KPH Ngawi Perum Perhutani Division Regional East Java.

Solano, J. y Villalobos, R. (2000). Regiones y subregiones climáticas de Costa Rica. San José, Costa Rica: Instituto Meteorológico Nacional.

Sulastri, R. (2015). Volume table of jati (Tectona grandis L. F.) using felled tree in Private Forest Standing (Case Study in Private Forest, Regency Kulon Progo Special Region Yogyakarta).

Tamarit, J., De los Santos, H., Aldrete, A., Valdez, R. y Ramírez, H., Guerra, V. (2013). Sistema de cubicación para árboles individuales de Tectona grandis L. F. mediante funciones compatibles de ahusamiento-volumen. Revista Mexicana de Ciencias Forestales, 5 (21), 59-75. DOI: 10.29298/rmcf. v5i21.358

Telles, R., Gómez, M., Alanís, E., Aguirre, O. y Jiménez, J. (2018). Ajuste y selección de modelos matemáticos para predecir el volumen fustal de Tectona grandis L. F. en Nuevo Urecho, Michoacán, México. Madera y Bosques, 24(3), 1-12. https://doi.org/10.21829/myb.2018.2431544

Tewari, V. P., Mariswamy, K. M. y Arunkumar, A. N. (2013). Total and merchantable volume equations for Tectona grandis Linn. F. plantations in Karnataka, India. Journal of Sustainable Forestry, 32(3), 213-229. https://doi.org/10.1080/10549811.2013.762187

Tewari, V. y Singh, B. (2018). Total Wood Volume Equations for Tectona grandis Linn F. Stands in Gujarat, India. Journal of Forest and Environmental Science, 34(4),313-320. https://doi.org/10.7747/JFES.2018.34.4.313

Torres Del Valle, E. y Restrepo, G. (2012). Site index for teak in Colombia. Journal of Forestry Research 23(3), 405–411. https://doi.org/10.1007/s11676-012-0277-x

Ureigho, U. y Akpobome, W. (2018). Models for volume estimation of Tectona grandis stands atoke-eri plantation in ijebu-ode, Ogun state, Nigeria. Nigerian Journal of Agriculture, Food and Environment, 14(1), 13-19.

Vaides, E., Ugalde, L. y Galloway, G. (2004). Crecimiento y productividad de teca en plantaciones forestales jóvenes en Guatemala. Recursos Naturales y Ambiente. 46-47,13

---