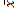Evaluación del crecimiento de Cedrela odorata L. en sistemas agroforestales con café en Pérez Zeledón, Costa Rica

Evaluation of the growth of Cedrela odorata L. in coffee agroforestry systems in Pérez Zeledón, Costa Rica

David Carvajal-Arroyo1, Rafael Murillo-Cruz2, Mariela González Rojas3,
William Fonseca-González4

[Recibido: 15 de abril 2020, Aceptado: 6 de octubre 2020, Corregido: 17 de octubre 2020, Publicado: 1 de enero 2021]

Resumen

[Introducción]: La combinación de árboles maderables con cultivos agrícolas presenta muchas ventajas a nivel de finca, más cuando las especies usadas poseen alto valor comercial. [Objetivo]: Se propuso evaluar el crecimiento de cedro amargo (C. odorata) en sistemas agroforestales con café mediante una caracterización dasométrica y el desarrollo de modelos alométricos para la predicción del volumen total por árbol. [Metodología]: Se establecieron 140 parcelas temporales rectangulares de 1 000 m2 con cedro entre uno y 20 años y se midió el diámetro a 1.3 m (DAP), la altura total (Ht) y comercial (Hc) de cada árbol. Se generaron 14 modelos que predicen el volumen total por árbol a partir del DAP, la edad y la altura; para el conjunto de edades (de 1 a 20 años) y para rangos (cada 5 años). También se generó un modelo de volumen comercial en función del DAP y otros relacionando las demás variables. [Resultados]: El modelo general predice el volumen total según el DAP con un R2=0.99 mientras que los modelos por rango de edad obtuvieron un R2 mayor a 0.95. El coeficiente de determinación del modelo de volumen comercial fue de 0.79 [Conclusiones]: Tanto el modelo general como el de rangos, predicen exitosamente el volumen, no obstante, el de rangos estima mejor el volumen total entre los 11 y 16 años, mientras que para el resto de las edades el modelo general es más recomendable.

Palabras clave: agroforestería; modelos de volumen total y comercial; parámetros estadísticos; regresión.

Abstract

[Introduction]: The combination of timber trees with agricultural crops has many advantages at the farm level, especially when the species used have high commercial value. [Objective]: Evaluate the growth of Spanish cedar (C. odorata) in coffee agroforestry systems using dasometric characterization and allometric models to predict the tree’s total and commercial volume. [Methodology]: A total of 140 1000 m2 temporary rectangular plots were established with one to 20-year-old cedar trees; in addition, the diameter of tree each at 1.3 m (DBH), total height (Ht), and commercial height (Hc) was measured. A total of 14 models were generated to predict total volume per tree using DBH, age, and height: for the set of ages (1 to 20 years) and ranges (every five years). A commercial volume model was also generated based on DBH and other elements connecting the other variables. [Results]: The general model predicts a total volume based on DBH with an R2= 0.99, while models by age range obtained an R2 greater than 0.95. The coefficient of determination of the commercial volume model was 0.79. [Conclusions]: Both the general model and the rank model successfully predict volume; however, the rank model better estimates the total volume between 11 and 16 years of age, while the general model is more recommended for the rest of the ages.

Keywords: Agroforestry; regression; statistical parameters; total-commercial volume models.

1. Introducción

En el mundo, cerca de la mitad de las fincas agrícolas tienen al menos un 10 % de su área con árboles de diferentes propósitos como la producción de madera, forraje, para sombra, para la fijación de nitrógeno, entre otras; esta forma de producción, catalogada como sistemas agroforestales (SAF), es importante tanto para la elaboración de productos locales como globales e, incluso, útil como estrategia para alcanzar objetivos nacionales (FAO, 2015; Sol, et al., 2018). La producción de madera en asocio con cultivos como cacao, café, plátano, banano, entre otros, posibilita un flujo de caja constante y los productos se ven menos afectados por condiciones de mercado (Moraga, 2006). Algunas especies maderables comúnmente utilizadas en estos sistemas son: Cedrela odorata L, Swietenia macrophylla King, Eucalyptus deglupta Blume, E. saligna Sm, Juglans olancheana Standl. & L.O. Williams y Cordia alliodora (Ruiz & Pav.) Cham.; además de las especies de servicio, como Erythrina fusca Lour. y las leguminosas de género Inga (Montenegro et al., 1997; Navarro et al., 2012).

En Costa Rica, el cedro amargo es una de las especies con mejor precio en el mercado y con alto valor, principalmente para mueblería (muebles de cocina y dormitorio), por su trabajabilidad; registró en el 2019 un valor de USD $ 140.2 m-3 en pie y
USD $ 413.1 m-3 en madera aserrada (Barrantes y Ugalde, 2019). Asimismo, la combinación de cedro amargo con café ha demostrado ser un sistema agroforestal exitoso, con un valor actual neto (VAN) de USD $ 14 083.82 ha-1, una tasa interna de retorno (TIR) de 16 % con respeto a una tasa de interés de 6.1 % y una relación de beneficio/costo de 1.34 (González et al., 2018).

En los últimos años, en Costa Rica se redujo el consumo de madera originaria de bosque natural y de sistemas agroforestales, mientras que el de las plantaciones forestales ha presentado un aumento. No obstante, la tasa de reforestación se redujo y, para el 2017, se registró la cifra históricamente más baja, con 2 002 hectáreas plantadas, según lo registrado por FONAFIFO (PEN, 2018); esto implica que el aporte de las plantaciones forestales a la producción de madera en el futuro se reducirá. Por otra parte, se ha comprobado que algunas especies logran mayor rendimiento en asocio con cultivos agrícolas que en rodales puros (Somarriba, et al., 2001), por lo que resulta conveniente cultivarlas con estos sistemas para incrementar la productividad de la finca. La combinación de café con especies maderables, como el cedro amargo, resulta en una opción de diversificación rentable para su producción (González et al., 2018); pero es necesario estimar el crecimiento de la especie en esta condición. Actualmente, el aporte de madera de los sistemas en terrenos de uso agropecuario, a la oferta del país es de 155 571 m3 en rollo (Barrantes y Ugalde, 2019).

En la combinación de cedro amargo con café hay escasa información, sin embargo, se reportan, para edades tempranas de un año, crecimientos de 4.4 cm en diámetro a la altura del pecho (DAP) y 2.7 m en altura total (Ht) en Turrialba, Costa Rica (Montenegro et al., 1997). A los 5 años, González et al. (2017) reportaron un diámetro medio de 15.77 cm y una altura total de 12.93 m; mientras que a los 10 años el diámetro y la altura superan los 25 cm y 17 m, respectivamente. Estos mismos autores registraron un volumen comercial máximo por árbol de 0.509 y 1.505 m3 a los 10 y 17 años, respectivamente, con una producción por hectárea de 92.13 m3, valor inferior al reportado para laurel (Cordia alliodora) con café, con un volumen total de 206 m3 ha-1 (132 m3 ha-1 de madera comercial) a los 20 años y una abundancia de 100 árboles ha-1 (Muschler, 2000).

En rodales puros de cedro, en el trópico en México a la edad de 15 años, se registraron volúmenes por árbol de 1.081 m3, una altura dominante máxima de 22.06 m y un diámetro promedio de 33.60 cm (Murillo et al., 2017). En Oaxaca, México, se generaron modelos de predicción de volumen con valores de 47 y 101 m3 ha-1 en sitios de baja y alta calidad, respectivamente (Larrea et al., 2008); mientras, en Honduras, se han obtenido rendimientos de 3.40 m3 árbol-1 en linderos asociados con café (Viera y Pineda, 2004).

La relevancia de los sistemas agroforestales en el país y en el mundo, el precio y las bondades del cedro motivaron la realización de este estudio, cuyo objetivo fue evaluar el crecimiento de la especie a distintas edades en SAF y desarrollar modelos de predicción del volumen. Adicionalmente, se generaron modelos para predecir el diámetro normal y la altura total y comercial.

2. Metodología

2.1.Localización y características del sitio

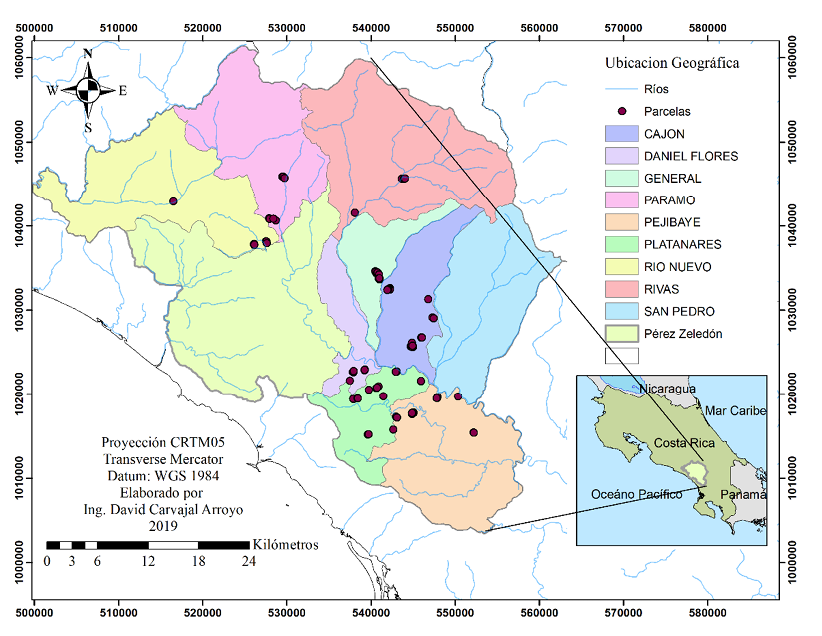
El área de estudio fue el cantón Pérez Zeledón, Costa Rica; específicamente en los distritos Cajón, General, Pejibaye, Platanares, Río Nuevo, Páramo, Daniel Flores, San Pedro y Rivas, en sitios entre 505 y 1 200 m snm (Figura 1). En Pérez Zeledón se encuentran varias zonas de vida, debido a su topografía y relieve; sin embargo, predomina en la mayor parte la superficie del cantón el bosque muy húmedo premontano (28.1 %) y el bosque pluvial premontano (18.5 %) con temperaturas promedio de 24 y 27 oC (INDER, 2016). La precipitación varía entre 2 000 y 4 000 mm anuales (Bolaños et al., 2005), son setiembre y octubre los meses más lluviosos según información del Instituto Meteorológico Nacional de Costa Rica (IMN, 2015).

Figura 1. Ubicación de los distritos donde se ubicaron las fincas con sistema agroforestal, Pérez Zeledón, Costa Rica, 2019.
Figure 1. Location of the districts where the farms with an agroforestry system were located, Pérez Zeledón, Costa Rica, 2019.

2.2. Muestreo

Con base en las fincas registradas por Coopeagri R.L., cuyos propietarios recibieron el pago por servicios ambientales (PSA) del Fondo de Financiamiento Forestal (FONAFIFO), en la modalidad de sistemas agroforestales (SAF), se elaboró una base de datos de fincas con cedro y café con edad entre uno y 20 años. Posteriormente, se visitaron las fincas y se instalaron parcelas de 1 000 m2 (25 x 40 m) que abarcan el rango de edades. En cada unidad de muestreo, para todos los árboles, se midió el diámetro a 1.3 m (DAP) con cinta diamétrica, y la altura total y la comercial con clinómetro. En total se midieron 2 059 árboles en 140 parcelas temporales en los periodos entre el 2017 y 2019 de las cuales 29 % se ubican en Platanares, 16 % en Pejibaye, 17 % en General, 14 % en Cajón, 10 % en Rio Nuevo, 7 % en Daniel Flores, 3 % en San Pedro y 2 % en Rivas y Páramo.

2.3 Procesamiento de información

Se elaboró una base de datos y se analizó gráfica y numéricamente para eliminar valores atípicos (árboles descopados, valor dudoso en alguna variable del árbol, etc.). Posteriormente se calculó el volumen total y comercial por árbol con la siguiente Ecuación 1 de la siguiente manera:

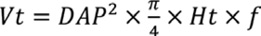(E.1)

Donde Vt= volumen total (m3), DAP= diámetro a 1.3 m (m), Ht= altura total (m) y f= factor de forma. Para todas las edades se utilizó un factor mórfico de 0.4 obtenido de una investigación en proceso en la misma zona.

El volumen comercial se calculó utilizando la misma fórmula con una altura comercial estimada con el clinómetro hasta un diámetro mínimo de 15 centímetros y un factor de forma de 0.6 obtenido de González et al. (2018) en su estudio de rentabilidad de cedro amargo en la misma zona.

2.4. Análisis estadístico

Se generaron los modelos de predicción del volumen total a partir del DAP, la edad y la altura: para el conjunto de edades de 1 a 20 años un modelo general y para 4 rangos de edades cada 5 años. Además, se generaron modelos de Ht en función del DAP y la EDAD; el DAP en función de la EDAD; y la Hc en función de la Ht, el DAP y la EDAD. Posteriormente, se analizaron los modelos del conjunto de edades con respecto a los modelos para los rangos de cada 5 años y se compararon estadísticamente con respecto a otros modelos existentes.

Los modelos se desarrollaron en STATGRAPHICS Centurion Version 16.1.18. Para elegir el mejor modelo se utilizó una metodología de normalización de parámetros estadísticos que incluyó: el coeficiente de determinación (R2), el error estándar del estimado (EEE), el error medio absoluto (EMA), la prueba de Durbin Watson (DW), cuadrado medio del error (CME), la diferencia agregada (DA), el índice de Furnival (IF), la sumatoria del cuadrado de los residuos (PRESS), el error porcentual (E %) y el criterio de información de Akaike (AIC). La escala de valoración de estos parámetros es diferente, especialmente cuando hay transformación de las variables dependientes, por lo tanto, no se pueden usar para crear un índice que permita una escogencia objetiva. La normalización consistió en definir una escala con rango de 0 a 1 para cada estadístico del modelo, y se creó un índice cuyo máximo valor representa a la mejor ecuación dentro del grupo de ecuaciones analizadas.

3. Resultados

3.1 Características dasométricas

En la cronosecuencia evaluada, el diámetro varió desde 0.8 a 73.8 cm, en plantaciones de 1 y de 20 años, respectivamente. La altura total y comercial máxima registrada fue de 29.88 m y 18.09 m, correspondientemente (Cuadro 1). Según el coeficiente de variación se registró, para todas las variables, una alta variabilidad principalmente en las plantaciones más jóvenes. En efecto, para el DAP y Ht, en cedro menor a 10 años, la variación fue de 31 y 28 % respectivamente; mientras que, para estas mismas variables, en cedro entre 10 y 20 años, la variación fue en promedio de 22 y 13 %. Entre los 17 y 20 años, el 40 % de los árboles poseen un diámetro de 40 a 50 cm y el 32 % supera los 50 cm. En este rango de edad es común que, en la zona, se realice el aprovechamiento de la madera en las fincas cafetaleras con cedro.

El volumen total promedio por árbol a los 20 años fue de 2.0746 m3 (±0.9849 m3) y un volumen máximo de 4.7273 m3, a esta edad la variación fue del 48 %. El volumen comercial varió entre 0.694 y 1.205 m3 entre los 17 y 20 años. En promedio, la relación volumen comercial y total fue de 53 % desde los 9 años hasta los 20 años.

Cuadro 1. Características dasométricas (diámetro, altura total y comercial, volumen total y comercial) en árboles de C. odorata en SAF, Pérez Zeledón, Costa Rica, 2019
Table 1. Dasometric characteristics (diameter, total and commercial height, total and commercial volume) in C. odorata trees in SAF, Pérez Zeledón, Costa Rica, 2019.

Edad (años)	n		Diámetro (cm)		Altura total (m)		Altura comercial (m)		Volumen total por árbol (m3)		Volumen comercial por árbol (m3)		Vt/Vc
	Parcela	Árboles		DE		DE		DE		DE		DE	%
1	3	32	3.92	1.19	3.20	0.86	-	-	0.002	0.01	-	-	-
2	8	134	3.95	1.38	3.53	1.47	-	-	0.002	0.01	-	-	-
3	5	96	6.79	2.97	6.00	2.15	-	-	0.013	0.02	-	-	-
4	5	151	9.01	3.05	7.31	2.16	-	-	0.024	0.02	-	-	-
5	5	53	15.72	2.17	12.99	2.23	-	-	0.105	0.04	-	-	-
6	12	281	11.59	3.71	9.84	2.80	-	-	0.052	0.04	-	-	-
7	8	149	15.61	5.51	11.04	2.96	-	-	0.107	0.09	-	-	-
8	11	145	18.90	6.53	13.08	3.46	-	-	0.186	0.16	-	-	-
9	8	130	23.95	6.25	16.35	3.40	6.41	2.26	0.337	0.22	0.201	0.17	59
10	19	311	25.72	6.19	19.02	4.38	8.10	3.02	0.446	0.27	0.284	0.17	64
11	10	100	28.71	7.99	18.65	4.12	6.93	3.16	0.566	0.41	0.335	0.23	59
12	7	154	30.46	7.60	19.66	4.29	8.64	3.47	0.653	0.46	0.438	0.22	67
13	6	74	32.67	7.84	21.86	3.43	11.30	3.34	0.807	0.46	0.658	0.29	82
14	3	25	41.90	5.91	23.75	3.02	9.74	3.52	1.361	0.47	0.806	0.25	59
15	5	64	34.69	7.80	23.64	3.76	10.96	3.26	0.973	0.51	0.693	0.28	71
16	5	75	34.93	7.47	21.35	3.34	9.19	2.25	1.642	0.44	0.576	0.22	35
17	5	44	42.66	10.75	28.08	4.66	9.94	2.05	1.758	1.01	0.947	0.36	54
18	3	35	43.26	5.83	24.46	3.86	8.21	2.48	1.486	0.56	0.740	0.21	50
19	5	45	44.70	10.60	24.95	3.82	10.00	3.64	1.655	0.78	1.094	0.51	66
20	7	56	49.56	10.84	24.93	3.06	11.80	2.96	2.074	0.98	1.448	0.43	70

n= tamaño de la muestra por edad, =promedio, DE= desviación estándar

3.1.1 Distribución diamétrica

A los 10 años, el 56 % de los árboles alcanzaron un DAP de 20 a 30 cm, a los 15 años el 66 % de 25 a 40 cm, entre 16 y 20 años el 53 % de 35 a 50 cm, con un volumen entre 0.8907 y 2.0250 m3. A los 20 años el 40 % de los individuos tiene un diámetro de 50 a 60 cm y el 14 % superó 60 cm (Cuadro 2).

Cuadro 2. Abundancia (árboles) de C. odorata por clase diamétrica y rango de edad en SAF, Pérez Zeledón, Costa Rica, 2019
Table 2. Abundance (trees) of C. odorata by diameter class and age range in SAF, Pérez Zeledón, Costa Rica, 2019.

Clase diamétrica (cm)	Edad (años)
	5 años	10 años	15 años	20 años
10 a 14.9	21	14	-	-
15 a 19.9	29	39	3	-
20 a 24.9	3	80	3	-
25 a 29.9	-	99	10	4
30 a 34.9	-	62	17	2
35 a 39.9	-	15	15	5
40 a 44.9	-	2	9	8
45 a 49.9	-	-	6	7
50 a 54.9	-	-	1	11
55 a 59.9	-	-	-	11
60 a 64.9	-	-	-	4
Mayor a 65	-	-	-	4

3.2 Modelos de predicción

En total se generaron 14 modelos según sus estadígrafos de los cuales 2 son modelos generales: uno para el volumen total y otro para volumen comercial; ambos utilizan como variable predictora el DAP. Además, para el volumen total se seleccionaron otros 2 modelos cuyas variables independientes son la EDAD y la altura total. Para cada rango de edad propuesto se obtuvo un modelo que predice el volumen en función del DAP. Finalmente, 6 modelos más que predicen el DAP, la Ht y Hc.

3.2.1 Modelos predictivos del DAP, Ht y Hc

Los modelos para estimar Ht y DAP poseen un coeficiente de determinación mayor al 0.77, mientras que los que predicen la Hc fueron inferiores al 0.37 (Cuadro 3). Cifras tan bajas en el ajuste indican que el crecimiento de la altura comercial de cedro no es explicado adecuadamente por las variables de DAP, Ht y EDAD.

La relación entre la Ht y el DAP con respecto a la EDAD muestra que ambas variables continúan creciendo aún a los 20 años (Figura 2), pero con una disminución más acelerada y, a menor edad, la altura. Por ejemplo, el DAP en promedio creció 2.30 cm año-1 en los primeros 10 años y aumentó a 2.60 cm año-1 entre los 10 y 20 años, mientras la Ht creció 1.81 y 0.93 m año-1 en el primer y segundo periodo, respectivamente. El mayor incremento corriente anual para el DAP se registró al año 20 (2.67 cm) y para la Ht al año 2 (2.53 m).

Cuadro 3. Modelos predictivos de la altura y el diámetro para árboles de C. odorata en SAF, Pérez Zeledón, Costa Rica, 2019
Table 3. Predictive models of height and diameter for C. odorata trees in SAF, Pérez Zeledón, Costa Rica, 2019.

Modelo	n			R2	EMA	DW	ECM	DA	IF	E%	AIC
Ht = (0.0803195 + 1.27971*ln(DAP))^2	2059			0.88	0.27	1.07	2.80	0.12	0.34	2.46	1.03
DAP = exp(0.614883 + 1.09388*ln(EDAD))	2059			0.80	0.26	0.81	6.53	0.89	0.33	6.13	1.88
Ht = (0.741368 + 1.46152*ln(EDAD)^2		2059	0.78		0.38	0.73	3.67	0.23	0.48	6.50	1.30
Hc = (-1.74375 + 1.55995*ln(Ht))^2	1096			0.36	0.38	1.15	2.99	0.50	0.49	7.71	1.10
Hc = exp(2.92842 - 23.5776/DAP)	1096			0.36	0.27	1.35	2.96	0.24	0.36	11.10	1.09
Hc = exp(3.18185 - 20.9741/EDAD)	1096			0.19	2.63	1.14	2.99	0.50	3.29	7.71	1.10

DAP= Diámetro A 1.3 m (cm), Ht= Altura total (m), Hc= altura comercial (m), n= tamaño de la muestra, R2= coeficiente de determinación, EMA= error medio absoluto, DW= prueba de Durbin Watson, CME=error cuadrático medio, DA=diferencia agregada, IF=índice de Furnival, E%= error porcentual, AIC= criterio de información de Akaike.

La relación DAP/Ht en los primeros años (1 a 6 años) fue cercana a 1 cm m-1, aumentó conforme el árbol envejecía hasta llegar a ser mayor a 2 cm m-1 de los 17 años en adelante. En promedio, entre 1 y 10 años la relación DAP/Ht fue de 1.20 cm m-1 y a partir de los 11 hasta los 20 años aumentó a 1.78 cm m-1.

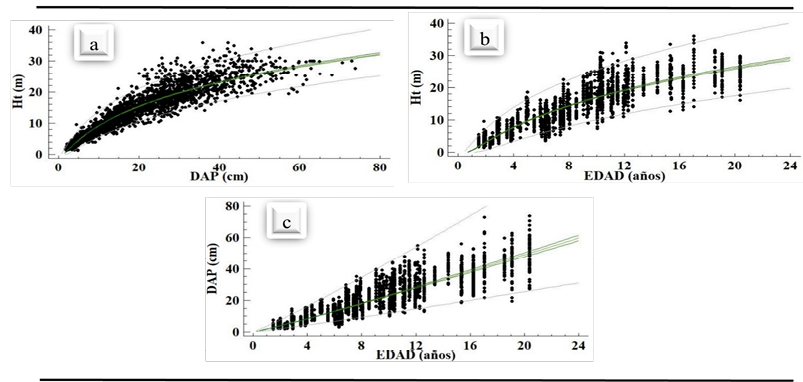
La relación entre la Hc y las otras variables (DAP, EDAD y Ht) fue positiva; a partir de 15 años, 24 m de Ht y 37 cm de DAP, la Hc es igual o superior a 10 m (Figura 3). Además, a partir de 16 m de Ht, la Hc representa en promedio el 41.4 % de la altura total, mientras que la relación Hc/DAP fue de 0.28 m cm-1. Es necesario tomar en cuenta que la variabilidad entre estas relaciones es amplia y que los modelos de volumen comercial no son apropiados desde el punto de vista estadístico, debido a su bajo ajuste en el coeficiente de determinación.

Figura 2. Modelos predictivos de la altura total y el DAP en árboles de C. odorata en SAF, Pérez Zeledón, Costa Rica, 2019: a) Ht en función DAP, b) Ht en función a la EDAD, c) DAP en función a la EDAD.
Figure 2. Predictive models of total height and DBH in C. odorata trees in SAF, Pérez Zeledón, Costa Rica, 2019: a) Ht as a function to DBH, b) Ht as a function AGE, c) DAP as a function AGE.

Figura 3. Modelos predictivos de la altura comercial de C. odorata en SAF, Pérez Zeledón, Costa Rica, 2019: a) en función del Ht, b) en función del DAP, c) en función de la EDAD.
Figure 3. Predictive models of the commercial height of C. odorata in SAF, Pérez Zeledón, Costa Rica, 2019: a) as a function of Ht, b) as a function of DAP, c) as a function of AGE.

3.2.2 Modelos generales para predecir el volumen

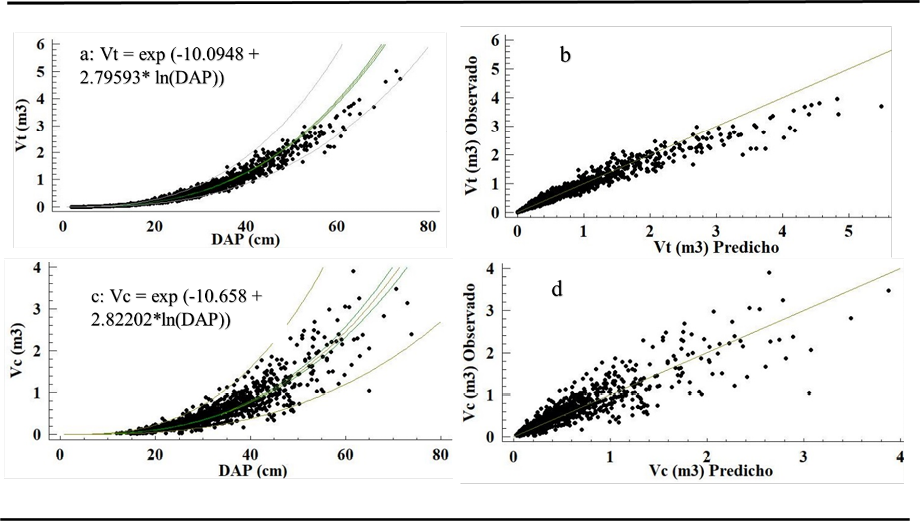
Los modelos para predecir el volumen total por árbol (Vt), desde uno hasta 20 años, en función del DAP, la Ht y la EDAD mostraron ajustes (R2) de 0.99, 0.85 y 0.71, respectivamente, lo que indica que el DAP es la variable que mejor explica la variabilidad observada en el volumen. El modelo que utiliza el DAP como variable independiente tiene la ventaja de que el DAP es una variable fácil de medir y con un margen de error menor, por lo cual es la mejor opción. Además, este modelo presentó las cifras más bajas de errores como el E% y EMC, en comparación con los demás modelos (Cuadro 4).

El modelo para el volumen comercial es útil para predecirlo a partir de los 9 años. Este presenta mejores parámetros estadísticos en comparación con los demás modelos, por ejemplo, es superior a los demás al tomar en cuenta EMA, IF y DA. También posee el segundo mejor AIC y coeficiente de determinación (R2). Tanto el volumen total y comercial presentan una relación lineal y aceptable, según la gráfica de volúmenes predichos y observados (Figura 4).

Cuadro 4. Modelos predictivos del volumen total y comercial para C. odorata en SAF, Pérez Zeledón, 2019
Table 4. Predictive models of the total and commercial volume for C. odorata in SAF, Pérez Zeledón, 2019.

Modelo	n	R2	DW	EMA	CME	IF	DA	E%	AIC
Vt = exp (-10.0948 + 2.79593*ln(DAP))	2059	99.1	1.173	0.149	0.170	0.195	0.022	2.01	-1.769
Vt = (0.0833394 + 0.001589*Ht^2)^2	2059	85.1	1.060	0.104	0.350	0.1579	0.024	2.84	-1.046
Vt= (0.65536 + 0.00341986*EDAD ^2) ^2	2059	71.3	0.976	0.164	0.396	0.2190	0.047	14.3	-0.918
Vc =exp(-10.658 + 2.82202*ln(DAP))	1096	86.1	1.356	0.276	0.240	0.365	0.014	7.76	-1.418

Vt= volumen total (m3), Vc= volumen comercial (m3), DAP= diámetro normal (cm), Ht= altura total (m), n= tamaño de la muestra, DW= prueba de Durbin Watson (P=0.000), CME= error cuadrático medio, IF=índice de Furnival, AIC, criterio de información de Akaike, R2= coeficiente de determinación, E%= error porcentual.

Figura 4. Modelos para predecir el volumen de C. odorata en SAF, Pérez Zeledón, 2019. a, b) modelo para el volumen total y distribución de los residuos; c, d) modelo para el volumen comercial y distribución de los residuos.
Figure 4. Models to predict the volume of C. odorata in SAF, Pérez Zeledón, 2019. a, b) model for the total volume and distribution of waste; c, d) model for commercial volume and distribution of waste.

3.2.3 Modelos predictivos del volumen total por rango de edad

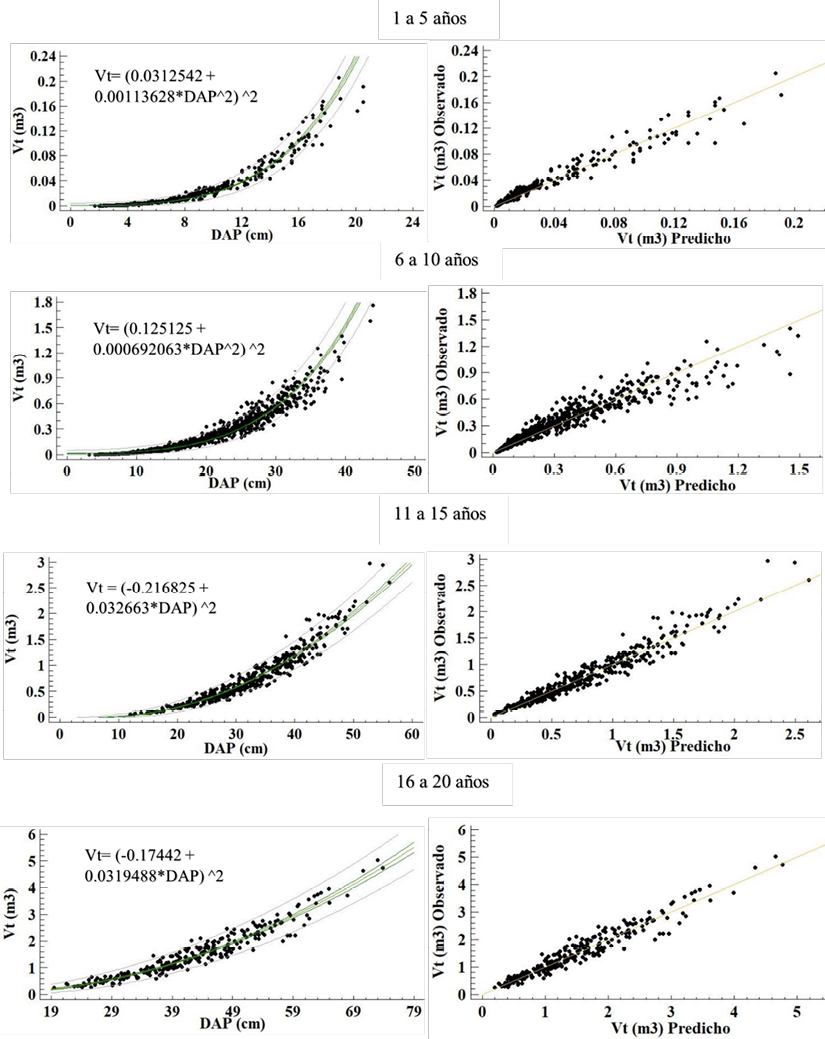
Los modelos elegidos mostraron un ajuste (R2) superior al 0.95 para todos los rangos de edad. El error de predicción o sesgo fue inferior o igual a 2 % entre los 10 y 20 años, pero poco precisos a edades inferiores (Cuadro 4). Los gráficos de residuos muestran una distribución lineal entre el volumen predicho y el observado (Figura 5).

Cuadro 5. Modelos para predecir el volumen total por rango de edad de C. odorata en SAF, Pérez Zeledón, Costa Rica, 2019
Table 5. Models to predict the total volume by age range of C. odorata in SAF, Pérez Zeledón, Costa Rica, 2019.

Rango (años)	Modelo	n	R2 (%)	DW	CME	IF	AIC	DA	E %
1 a 5	Vt= (0.0312542 + 0.00113628*DAP^2)^2	421	96.5	1.279	0.009	0.018	-4.56	0.003	10.14
6 a10	Vt=(0.125125 + 0.000692063*DAP^2)^2	966	95.0	1.081	0.071	0.053	-2.62	0.003	5.42
11 a 15	Vt = (-0.216825 + 0.032663*DAP)^2	417	94.9	0.990	0.123	0.063	-2.07	0.004	1.12
16 a 20	Vt= (-0.17442 + 0.0319488*DAP)^2	255	96.4	1.031	0.229	0.091	-1.44	0.008	1.99

Vt= volumen total (m3), DAP= diámetro normal (cm), n= tamaño de la muestra, R2= coeficiente de determinación, DW= prueba de Durbin Watson, CME= error cuadrático medio, IF=índice de Furnival, AIC, criterio de información de Akaike, DA=diferencia agregada, E%= error porcentual.

Figura 5. Modelos para predecir el Vt y distribución de residuos de C. odorata en SAF para cuatro rangos de edad, Pérez Zeledón, Costa Rica, 2019.
Figure 5. Models to predict the Vt and residue distribution of C. odorata in SAF for four age ranges, Pérez Zeledón, Costa Rica, 2019.

3.2.4 Comparación entre modelos generales y por rango de edad

El modelo general y los modelos por rango subestiman el volumen total en la mayoría de las edades con un error porcentual promedio del 12 %, en este sentido, para las primeras etapas de crecimiento los modelos subestiman hasta 25 y 35 %. Únicamente a los 18 y 20 años el modelo general sobreestima el volumen con un error de 4.28 y 9.25 %, respectivamente, y a los 16 años el modelo de rango lo sobreestima en un 1.25 %. Para todos los modelos, los errores de estimación más altos se presentan a edades tempranas (menor de 10 años), cuando la madera comercial muestra un porcentaje bajo, porque el árbol está en crecimiento (Cuadro 6).

Cuadro 6. Comparación entre modelos de predicción de volumen total por árbol y el volumen real observado de C. odorata en SAF, Pérez Zeledón, Costa Rica
Table 6. Comparison between prediction models of total volume per tree and the actual observed volume of C. odorata in SAF, Pérez Zeledón, Costa Rica.

Edad	DAP Observado (cm)	Vt Observado (m3)	Vt Modelo general (m3)	E%	Vt Modelo por rango (m3)	E%
2	3.95	0.0024	0.002	-19.88	0.002	-0.03
4	9.01	0.0238	0.019	-18.97	0.015	-35.92
6	11.59	0.052	0.039	-25.01	0.048	-8.53
8	18.9	0.1863	0.153	-17.86	0.139	-25.59
10	25.72	0.4463	0.362	-18.85	0.340	-23.86
12	30.46	0.6526	0.581	-10.95	0.605	-7.23
14	41.9	1.3606	1.417	4.17	1.327	-2.50
16	34.93	0.8756	0.852	-2.67	0.887	1.25
18	43.26	1.4861	1.550	4.28	1.459	-1.86
20	49.56	2.0746	2.266	9.25	1.985	-4.31

*Los modelos por rango de edad corresponden a cada 5 años (Cuadro 5).

4. Discusión

4.1 Caracterización dasométrica

El volumen total por árbol obtenido en este estudio (2.0746 m3, con DAP de 49.56 cm y Ht de 24.93 m a los 20 años) fue un 40 % menor que lo registrado por Viera y Pineda (2004), quienes indican 3.40 m3 con 77.56 cm en diámetro, a la misma edad, en linderos asociados con café. La diferencia puede ser explicada por el origen de los datos, por ejemplo, la calidad del sitio, de los datos registrados a 20 años en Pérez Zeledón corresponde al distrito de Cajón, cuyas características edafoclimáticas se encuentran por debajo de las condiciones óptimas determinadas por González et al. (2017) para el desarrollo de cedro en sistemas agroforestales con café en la misma zona, tales como los niveles de pH, la altitud y la relación calcio-magnesio. Otras posibles causas de las diferencias en volumen están relacionadas con el manejo silvicultural, el programa de fertilización y encalado, así como con el tipo de arreglo en el sistema agroforestal. Además, la muestra utilizada por Viera y Pineda (2004) fue de 8 árboles, la cual podría no ser representativa, mientras que en el presente estudio se utilizaron 56 individuos en esa edad.

Caso contrario registró Murillo et al. (2017) en rodales puros en México, con cifras de 1.081 m3 con un diámetro de 33.6 cm a los 15 años. En este caso, la altura (22.06 m) y el diámetro normal promedio son inferiores a lo obtenido en el presente estudio; pero el volumen total por árbol es superior en un 10 % para la misma edad. Al no concordar la comparación entre el volumen y las variables mencionadas entre los estudios, podrían existir diferencias en el cálculo de volumen, como el uso de un factor de forma mayor a 0.4. A los 17 años, el volumen comercial (0.947 m3) calculado en este trabajo es inferior al registrado por González et al. (2018) en sistemas agroforestales con café (1.204 m3) lo que se podría deberse a la inclusión de datos de otras calidades de sitio producto de una mayor cantidad de árboles incorporados a la muestra.

Para la misma zona en Pérez Zeledón, Calvé et al. (2020) registraron una diferencia de DAP (39.9 cm) con respecto al presente estudio, superior en aproximadamente 6 cm. La diferencia puede estar referida a la cantidad de árboles registrados en los estudios y a la calidad del sitio donde se realizó la medición.

4.2 Modelos predictivos del DAP, Ht y Hc

Entre los modelos para predecir la Hc, los que utilizan el DAP y la Ht como variables predictoras proporcionan estimaciones más cercanas al valor observado, sobreestiman en promedio la Hc en un 4.1 y 3.9 %, respectivamente. Al utilizar la EDAD como variable predictora, el error porcentual promedio del modelo es superior al 40 %, lo cual indica que el uso del modelo no es adecuado. Entre 10 y 20 años, los modelos que predicen la Ht y DAP en función de la EDAD tienden a subestimar el volumen en un 4 %, mientras para edades tempranas (uno a 9 años) la subestimación es de 10 a 12 %.

El ajuste logrado (R2 >0,80) en este estudio para predecir Ht y DAP es superior al registrado por Jiménez (2012) para C. odorata (0.68) en cafetales en Honduras, quien utilizó el modelo de Chapman y Richards para predecir la relación entre el DAP y la EDAD. También, el modelo mostró ser superior en ajuste a lo registrado por Inga y del Valle (2017), quienes obtuvieron una eficiencia de 0.65 utilizando una regresión no lineal para cedro y caoba.

4.3 Modelos predictivos del volumen

El ajuste (R2=0.99) del modelo para predecir el volumen total en función del DAP en el presente estudio fue muy satisfactorio y similar al obtenido por Larrea et al. (2008) en la determinación del volumen total para C. odorata en México, también este fue similar al logrado con otras especies; por ejemplo, R2=0.98 con teca clonal (Fallas, 2017) y a lo registrado por Hernández et al. (2017) en plantaciones de Eucalyptus urophylla. Cifras tan altas de R2 son indicadoras de que el DAP es una excelente variable predictora del volumen, con la ventaja de que su medición es muy fácil y objetiva.

Para el volumen comercial de cedro en cafetales, González et al. (2018) eligieron un modelo de regresión múltiple con un valor de R2 de 0.90 y un CME de 0.019 m3. Para melina (Gmelina arborea), Quirós (2015) logró un ajuste de 0.89 con un EEE de 0.035; mientras, para teca clonal, Fallas (2017) obtuvo un R2 de 0.98; en las 3 investigaciones, los modelos elegidos para predecir el Vc en función del DAP presentaron valores en el coeficiente de variación ligeramente superiores que los obtenidos en el presente estudio.

La predicción del volumen comercial está sujeta a la alta variabilidad de la altura comercial, por lo cual el ajuste de los datos no supera el 0.86; sin embargo, las proyecciones de volumen presentan errores porcentuales bajos (menor a 7.76 %) que permiten que el modelo sea confiable y apropiado en sistemas agroforestales con cedro a partir de los 9 años. La variación, tanto para este modelo como para las variables dasométricas, responden a una variedad de espaciamiento, manejo y tipos de sistemas agroforestales presentes en la zona de estudio.

5. Conclusiones

El crecimiento de cedro en sistemas agroforestales (SAF) con café a los 20 años en la zona evaluada alcanzó un DAP promedio de 50 cm, una altura total y comercial de 25 y 11.8 m respectivamente. Los modelos de volumen total y comercial basados en la variable DAP son precisos y adecuados en comparación con los modelos que utilizan las variables de altura total, comercial y edad; además, la medición en campo del DAP es menos susceptible a errores, lo cual la convierte en una variable predictora efectiva para la estimación del volumen.

Para la determinación del volumen total por árbol, se recomienda el uso del modelo general cuando la edad de cedro es menor a 11 años y mayor a 16 años, mientras que cuando la edad se ubica entre los 11 y 16 años, se podría utilizar el modelo generado dentro del rango de edad correspondiente. En futuros trabajos relacionados con la selección de modelos, se sería interesante la aplicación de la metodología de normalización de parámetros estadísticos, utilizada en este estudio, dado que proporciona una selección objetiva.

6. Ética y conflicto de intereses

Las personas autoras declaran que han cumplido totalmente con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en la producción del manuscrito; que no hay conflictos de intereses de ningún tipo; que todas las fuentes financieras se mencionan completa y claramente en la sección de agradecimientos; y que están totalmente de acuerdo con la versión final editada del artículo.

7. Agradecimientos

Se agradece a los sujetos caficultores del cantón de Pérez Zeledón que participaron en el estudio y permitieron la recolección de la información. A CoopeAgri R. L. y al INISEFOR-UNA, por el apoyo logístico y financiero para la realización de esta investigación. También se agradece a la Revista y a las personas revisoras anónimas por sus oportunos comentarios.

8. Referencias

Barrantes, A. y Ugalde, S. (2019). Usos y aportes de la madera: Estadísticas 2018 y precios 2019. Oficina Nacional Forestal. https://onfcr.org/wp-content/uploads/2019/11/USOS-Y-APORTES-DE-LA-MADERA-2018.pdf

Bolaños, R., Watson, V. y Tosi, J. (2005). Mapa ecológico de Costa Rica (zonas de vida), según el sistema de clasificación de zonas de vida del mundo de L. R. Holdridge, Escala 1:750 000. Centro Científico Tropical.

Calvé Jarque, S., Murillo, O., Salazar, L., & Córdoba, D. (2020). Aporte económico de la madera de cedro (Cedrela odorata L.) como árbol de sombra en cafetales de Pérez Zeledón, Costa Rica. Revista Forestal Mesoamericana Kurú, 17(41), 68-77. https://doi.org/10.18845/rfmk.v17i41.5287

Fallas Zúñiga, J. (2017). Funciones alométricas, de volumen y de crecimiento para clones de teca (Tectona grandis L.f) en Costa Rica [Tesis de maestría] Escuela de Ingeniería Forestal, Instituto Tecnológico de Costa Rica.

FAO. (2015). Promoviendo la agroforestería en la agenda política: Una guía para tomadores de decisiones. Documentos de trabajo en Agroforestería No. 1Organización de la Naciones Unidas para la Alimentación y la Agricultura (FAO).

González, M., Murillo, R. y Ávila, C. (2018). Rentabilidad financiera de Cedrela odorata L. en sistemas agroforestales con café en Pérez Zeledón, Costa Rica. Revista de Ciencias Ambientales, 52(1), 129-144. http://kimuk.conare.ac.cr/Record/RUNA_f0c6c62c49db4927f94b2a4396d9b2f3

González, M., Murillo, R., Virginio, y Ávila, C. (2017). Influencia de factores biofísicos y de manejo en el crecimiento de Cedrela odorata L. en asocio con café en Pérez Zeledón, Costa Rica. http://kimuk.conare.ac.cr/Record/RTEC_1d8dfb9006e9b6ce3fb8750b4352e6cd

Hernández-Ramos, J., De los Santos-Posadas, H. M., Valdez-Lazalde, J. R., Tamarit-Urias, J. C., Ángeles-Pérez, G., Hernández-Ramos, A., Méndez-López, B., & Peduzzi, A. (2017). Estimación del volumen comercial en plantaciones de Eucalyptus urophylla con modelos de volumen total y de razón. Agro-Ciencia, 51(5), 561–580.

IMN. (2015). Pronóstico Climático Estacional Octubre-diciembre, 2015. Instituto Meteorológico Nacional. https://www.imn.ac.cr/documents/10179/29808/PerspClimCR201510.pdf/98f8c05e-604d-46a3-a4f9-ee2e4532ba55?version=1.1

INDER. (2016). Caracterización del territorio de Pérez Zeledón. Instituto de Desarrollo Rural. Dirección Región Brunca Oficina Subregional San Isidro https://www.inder.go.cr/territorios_inder/region_brunca/caracterizaciones/Caracterizacion-territorio-Perez-Zeledon.pdf

Inga, J. y del Valle, J. (2017). Log-relative growth: A new dendrochronological approach to study diameter growth in Cedrela odorata and Juglans neotropica, Central Forest, Peru. Dendrocronologia, 44(1), 117-129. https://doi.org/10.1016/j.dendro.2017.03.009

Jiménez Nehring, N. G. (2012). Producción de madera y almacenamiento de carbono en cafetales con cedro (Cedrela odorata) y caoba (Swietenia macrophylla) en Honduras. [Tesis de maestría] Centro Agronómico Tropical de Investigación y Enseñanza: CATIE.

Larrea, R. G., Posadas, H. M. de los S., y Hernández, J. I. V. (2008). Crecimiento y rendimiento de Cedrela odorata L. y Tabebuia donnell-smithii Rose en San José Chacalapa, Pochutla, Oaxaca. https://search-ebscohost-com.una.idm.oclc.org/login.aspx?direct=true&AuthType=ip,uid,url&db=asn&AN=35903276&lang=es&site=ehost-live

Montenegro, J., Ramírez, G. y Blanco, H. (1997). Evaluación del establecimiento y crecimiento inicial de seis especies maderables asociadas con café. Agroforestería en las Américas, 4(13):14-20.

Moraga, F. (2006). Alternativas de diversificación para caficultores frente al impacto de TLC. Universidad Nacional Autónoma de Nicaragua. http://repositorio.unan.edu.ni/7180/1/6604.pdf

Murillo, Y., Domínguez, M., Martínez, P., del C. Lagunes, L., y Aldrete, A. (2017). Índice de sitio en plantaciones de Cedrela odorata en el trópico húmedo de México. Revista FCA UNCUYO, 49(1), 15-30. https://search-ebscohost-com.una.idm.oclc.org/login.aspx?direct=true&AuthType=ip,uid,url&db=asn&AN=124007809&lang=es&site=ehost-live

Muschler, R. (2000). Árboles en cafetales. Centro Agronómico Tropical de Investigación y Enseñanza (CATIE). Proyecto Agroforestal CATIE/GTZ. Módulo de enseñanza, 45, 139. CATIE.

Navarro-Garza, H., Santiago, A., Musálem M., Vibrans H. y Pérez M. (2012). La diversidad de especies útiles y sistemas agroforestales. Revista Chapingo Serie Ciencias Forestales y del Ambiente 18(1), 71-86, 2012. https://doi.org/10.5154/r.rchscfa.2010.11.124

PEN. (2018). Estado de la nación en desarrollo humano sostenible. Programa Estado la Nación. https://estadonacion.or.cr/informes/

Quirós-Monge, S. (2015). Modelos de volumen comercial, perfil de fuste y crecimiento para plantaciones clonales de Gmelina arborea Roxb. ex Sm. en Costa Rica. http://kimuk.conare.ac.cr/Record/RTEC_46301c09feb2b41c9554bea6042d98f3

Sol-Sánchez, A., López-Juárez, S., Córdova-Ávalos, V., y Gallardo-López, F. (2018). Productividad potencial del SAF cacao asociado con árboles forestales. Revista Iberoamericana De Bioeconomía y Cambio Climático, 4(7), 862-877. https://doi.org/10.5377/ribcc.v4i7.6327

Viera, C. J., y Pineda, A. (2004). Productivity of Cedrela odorata living fences. http://kimuk.conare.ac.cr/Record/PUCR_cc1cbf9fc3d30334df030048f03f2ff9

---