Análisis comparativo de susceptibilidad de erosión y evaluación de incertidumbre en la subcuenca del Río Claro, Costa Rica

Comparative analysis of erosion susceptibility and an uncertainty evaluation at thesub-basin of the Claro River, Costa Rica

Iván Pérez-Rubio1, Daniel Flores2, Christian Vargas3, Andreas Mende4, Francisco Jiménez5

[Recibido: 21 de marzo 2020, Aceptado: 6 de octubre 2020, Corregido: 29 de octubre 2020, Publicado: 1 de enero 2021]

Resumen

[Introducción]: La deforestación y la gestión insostenible de los sistemas de producción agrícola y ganadero en áreas montañosas han provocado la degradación de la tierra y una progresiva reducción en la provisión de los servicios ecosistémicos. [Objetivo]: En este artículo se desarrolla un análisis espacial de susceptibilidad de erosión en la subcuenca del río Claro, en el cordón montañoso Fila Cruces, en la región del Pacífico Sur de Costa Rica. [Metodología]: Para ello se aplicaron los métodos de regresión logística y redes neuronales artificiales integrados en un entorno de sistemas de información geográfica (GIS) y empleando herramientas de teledetección. En ambos modelos se consideraron los siguientes factores explicativos: uso del suelo, geomorfología, pendiente, distancia euclidiana a la red de drenaje e índice de vegetación diferencial normalizado (NDVI, en sus siglas en inglés). Los mapas de susceptibilidad de erosión fueron validados independientemente por medio de la función características operativas del receptor (ROC, por sus siglas en inglés). [Resultados]: El modelo de redes neuronales artificiales obtuvo un poder predictivo superior al de regresión logística con base en el valor calculado del área debajo de la curva (AUC, por sus siglas en inglés). Los factores con mayor poder explicativo variaron en función del modelo utilizado [Conclusiones]: Los mapas de susceptibilidad de erosión mostraron una elevada alteración ecológica en términos de la probabilidad de ocurrencia de procesos de erosión, especialmente en la parte alta de la subcuenca, en terrenos ocupados por fincas de ganadería extensiva y elevada pendiente.

Palabras clave: Ganadería; redes neuronales artificiales; regresión logística; subcuenca hidrográfica; teledetección.

Abstract

[Introduction]: Deforestation and unsustainable management of agricultural and livestock production systems in mountainous areas have caused land degradation and a progressive reduction in the provision of ecosystem services. [Objective]: This paper elaborates erosion susceptibility mapping applied at the local scale in the Claro river subbasin in the Fila Cruces mountain range, in Southern Pacific Costa Rica. [Methodology]: The spatial analysis was conducted using a geographic information system (GIS) employing two techniques, logistic regression and artificial neural networks, as well as remote sensing tools. Five conditional factors were finally evaluated for the models: land use, geomorphology, slope gradient, distance to streams, and the Normalized Difference Vegetation Index (NDVI). The erosion susceptibility maps were validated through the receiver operating characteristics (ROC) function. [Results]: The artificial neural network model showed higher predictive power than the logistic regression method based on the calculated value of the Area under the Curve (AUC). The factors with the greatest explanatory power varied depending on the model used. [Conclusions]: The erosion susceptibility maps showed a high ecological alteration in terms of the probability of occurrence of erosion processes, especially in the upper subbasin, lands mostly occupied by cattle ranching, and a steeply sloped morphology.

Keywords: Artificial neural networks; cattle ranching; logistic regression; remote sensing; subbasin.

1.Introducción

La erosión del suelo es uno de los problemas más graves, desde un punto de vista ecológico y económico, que enfrentan los países tropicales (Bayard et al., 2006). Uno de los factores antrópicos que desencadenan incrementos dramáticos de erosión y producción de sedimentos es la deforestación de los bosques nativos en las cuencas hidrográficas tropicales (Bruijnzeel, 2004). En América Latina y el Caribe, la ganadería es uno de los principales usos del suelo; en Centroamérica cerca de 48 % de su extensión se utiliza para pastoreo (Steinfeld, 2002); 9 millones del total de hectáreas fueron transformadas de bosque a pasturas y monocultivos, las cuales presentan un alto nivel de degradación de suelos (Szott et al., 2000).

Esta problemática se presenta en la cadena montañosa Fila Cruces, localizada en el Pacífico Sur de Costa Rica. Se trata de un ecosistema relevante por su conectividad biológica, con un alto endemismo ecológico y amenazado por procesos de deforestación, cuyas tierras han sido ocupadas principalmente por ganadería extensiva y una agricultura de subsistencia (ProDUS 2007). Estas actividades humanas han derivado en una progresiva fragmentación del bosque húmedo tropical y una severa alteración del equilibrio hidrológico, cuyos efectos se traducen en erosión, riesgo de deslizamientos e inundaciones en las poblaciones locales, y sedimentación en el Golfo Dulce que afecta los arrecifes de coral (Cortés, 1990).

Son múltiples los estudios de análisis de susceptibilidad y de medición del riesgo o amenaza de deslizamientos de tierra. En términos generales, un análisis de susceptibilidad con respecto a un determinado terreno se refiere a la probabilidad de ocurrencia de un proceso de erosión. Ambas temáticas se diferencian en que estos últimos incluyen tanto factores condicionantes, que son variables intrínsecas del terreno, como factores activadores, variables extrínsecas como son las precipitaciones o las fallas tectónicas (Van Westen et al., 2003).

En los modelos de susceptibilidad y en los de amenaza se emplean diferentes herramientas estadísticas entre las cuales se encuentran las siguientes: ponderaciones de evidencia en modelos estadísticos bivariados (Van Westen et al., 2003), regresión logística binaria (Ayalew y Hamagishi, 2005; Lee et al., 2016) y probabilidad condicional conjunta mediante el teorema de Bayes (Chung y Fabbri, 1993). Recientemente se han introducido nuevos enfoques no lineales como las redes neuronales artificiales (Dou et al., 2015; Lee et al., 2016; Nefeslioglu et al., 2008; Pradhan y Lee, 2010). Más novedosos son los métodos de aprendizaje automático (machine learning) como los algoritmos de árboles de decisión (Pradhan, 2013) y máquinas de soporte vectorial (Dou et al., 2015; Pradhan, 2013).

A diferencia de estos estudios, en los cuales se abordan, específicamente, los deslizamientos del terreno, el presente trabajo se planteó como un análisis espacial de susceptibilidad aplicado sobre procesos genéricos de erosión, incluidos los deslizamientos. El propósito de esta elección consistió en evaluar el estado de conservación de la subcuenca hidrográfica en términos de la vulnerabilidad del suelo a eventos de erosión y su relación con un conjunto de factores condicionantes.

Los resultados obtenidos mediante los modelos de predicción deben ser convenientemente validados, en el sentido de evaluar su grado de correspondencia con la realidad. Al respecto, el método más utilizado es el denominado características operativas del receptor (ROC, en sus siglas en inglés) (Swets, 1998).

Los sistemas naturales muestran un comportamiento intrínseco difícil de predecir y simular, dado el amplio conjunto de factores que intervienen y cuya presencia, conocimiento o magnitud no es posible conocer a la perfección (Funtowicz y Ravetz, 1990). Evaluar la incertidumbre es una tarea compleja, si se consideran las múltiples aristas y dimensiones que puede encerrar el concepto (Hamel y Bryant, 2017). Por todo ello, se debe evaluar previamente la importancia relativa de las posibles fuentes de incertidumbre, delimitar su valoración y seleccionar adecuadamente las técnicas y herramientas apropiadas para su medición (Refsgaard et al., 2007).

El presente estudio aborda los siguientes propósitos. En primer lugar, un análisis comparativo del índice de susceptibilidad de erosión mediante los métodos de regresión logística y redes neuronales artificiales. En segundo lugar, un análisis de incertidumbre aplicado sobre el modelo de regresión logística a partir de la apreciación de error o un comportamiento aleatorio en las variables explicativas uso y coberturas del suelo y el índice de vegetación NDVI.

2.Metodología

2.1Área de estudio

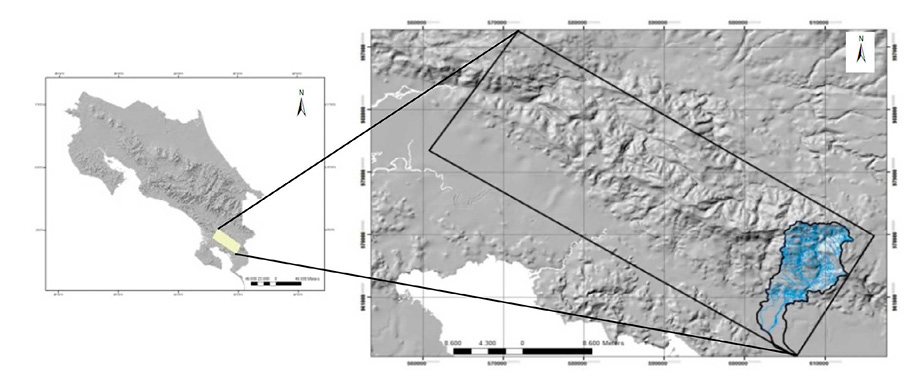
El área de estudio abarca una extensión de 100.81 km² y un perímetro de 62.27 km correspondientes a la subcuenca hidrográfica del Río Claro que forma parte de la Cordillera Costeña, sector Fila Cruces, en el Pacífico Sur de Costa Rica. La subcuenca se localiza entre las coordenadas geográficas 8º 40’ – 8º 47’ 30’’ Latitud Norte y 82º 57’ 30’’– 83º 4’ 30’’ Longitud Oeste (Figura 1).

Figura 1. Localización geográfica de cordillera Fila Cruces y la subcuenca hidrográfica del Río Claro.
Figure 1. Map of the Fila Cruces mountain range and the Claro river sub-basin.

2.2Procesamiento preliminar de sensores remotos

Los procesos de clasificación de los usos y coberturas del suelo y el cálculo del índice de vegetación normalizada requieren del preprocesamiento de las imágenes obtenidas mediante sensores remotos. Las imágenes utilizadas consistieron en fotografías aéreas correspondientes al Proyecto CARTA (2005) y dos imágenes del proyecto Landsat (path=14, row=54), Landsat-7 (ETM) adquirida el día 15/03/2005 y Landsat-8 (OLI TIRS) adquirida el día 14/01/2015. Las imágenes de Landsat fueron descargadas del United States Geological (USGS) Earth Explorer (https://earthexplorer.usgs.gov/).

Todas las imágenes Landsat fueron georreferenciadas al datum WGS_84 y al sistema de coordenadas Universal Transverse Mercator (UTM) Zona 17 Norte y tamaño de pixel de 30m. Las imágenes satelitales Landsat-7 y Landsat-8 se emplearon ambas para realizar una clasificación supervisada del uso del suelo y el cálculo del índice de vegetación diferencial normalizado (NDVI). Además, se descargó un mosaico de imágenes de Google Maps por medio del software SASPlanet 141212.8406 Staple (http://sasgis.org) pertenecientes al año 2014 que se emplearon para la digitalización de los usos del suelo observables mediante el programa ArcGIS 10.2.

Se utilizaron imágenes alternativas (±1 año), lo cual se explica a partir de un criterio de selección de aquellas imágenes con la menor presencia de nubes posible y que permitan, por lo tanto, una mayor precisión tanto en la clasificación de usos del suelo como en el cálculo del índice NDVI.

Las imágenes procedentes de los sensores remotos satelitales deben ser previamente procesadas para su utilización posterior. El primer paso consiste en convertir los valores originales presentes en formato digital number (DN) a valores de radianza. Los DN representan la intensidad de energía electromagnética medida por el sensor para un área de superficie terrestre. En el segundo paso se deben convertir los valores de radianza en valores de reflectancia (Chandler et al., 2009). Los valores de reflectancia se expresaron en el rango 0,1. Este procedimiento se implementó utilizando los programas ENVI 5.3 y ArcGIS 10.2.

2.3Inventario de procesos de erosión

El primer paso para la elaboración de la base de datos comienza con un inventario de los procesos de erosión (laminar, surco, cárcava o deslizamiento) observables dentro de la subcuenca del Río Claro. Para determinar su localización espacial se utilizaron sensores remotos, en concreto, fotografías aéreas correspondientes al Proyecto CARTA (2005) y Google Maps (2014), en una escala comprendida entre 1:5 000 y 1:25 000.

2.4Factores condicionantes

Dado que el presente estudio es un análisis de susceptibilidad y no un análisis de amenazas, no se incluyeron factores activadores como las precipitaciones o las fallas tectónicas (Van Westen et al., 2003). Se consideró, inicialmente, el siguiente conjunto de factores condicionantes con base en la bibliografía, los datos disponibles en el área de estudio y la escala de trabajo: ángulo de pendiente, dirección de pendiente, subunidades geomorfológicas del terreno (TMS, en sus siglas en inglés), altitud, geología, distancia a la red de drenaje, índice de vegetación diferencial normalizado NDVI, en sus siglas en inglés), tipo de suelo, usos y coberturas del suelo. El modelo de elevación digital, que permite el cálculo de las variables topográficas del modelo, fue construido mediante la interpolación de un mapa de contorno de curvas de nivel en intervalos de 10 metros (MINAE-CENIGA, 1998). La construcción espacial de estas variables se detalla a continuación (Figura 3):

1.Usos y coberturas del suelo. Los mapas de clasificación de uso del suelo fueron elaborados mediante la técnica de fotointerpretación-digitalización sobre la imagen aérea de Google Maps (2014), a una escala 1:5 000. Los porcentajes de la extensión de cada una las clases se muestran en el Cuadro 1.

2.Pendiente. Este mapa fue generado en una escala de 1:5 000 a partir de un modelo digital de elevación, el cual fue obtenido mediante una interpolación de contorno de curvas de nivel en intervalos de 10 metros (MINAE-CENIGA, 1998).

3.Subunidades geomorfológicas del terreno (TMS, en sus siglas en inglés). El mapa fue obtenido a partir de datos tomados en el campo (Mende y Astorga, 2007). Consiste en una clasificación del terreno que consta de 29 clases a partir de datos geomorfológicos, edáficos y geológicos subdivididos en unidades homogéneas que incorporan las siguientes variables: (1) ángulo de pendiente, (2) relieve relativo, (3) dirección de pendiente y (4) densidad de drenaje.

4.Distancia a la red de drenaje. A partir de la digitalización de la red de drenaje sobre la imagen del Proyecto CARTA (2005), se calculó la distancia euclidiana, y se generó una capa tipo ráster de 10 metros de cuadrícula.

5.Índice de vegetación diferencial normalizado (NDVI). Los valores del índice oscilan en un rango de [-1,1] y, para este caso, fueron convertidos en un rango de [0,1] con el objetivo de lograr, por una parte, una escala homogénea para todas las variables explicativas en el modelo de regresión logística y, en segundo lugar, analizar su relación con los valores de susceptibilidad de erosión.

Para la selección de las variables, se realizó un análisis bivariado que se concretó en un análisis de correlación para las variables numéricas y en un contraste de dependencia X² para las cualitativas. Este análisis se aplicó en dos sentidos, por una parte, entre la variable dependiente y cada una de las variables independientes, así como entre las variables independientes entre sí con el propósito de detectar la presencia de multicolinealidad (para el modelo de regresión logística). Siguiendo este procedimiento se rechazaron, para el modelo final, las siguientes variables: dirección de pendiente, geología y la tipología de suelo. En relación con esta última, la razón se basó en la disponibilidad de un único mapa en escala 1:500 000. La base de datos espaciales generada en formato raster por medio del programa ArcGIS 10.2 fue exportado en formato ASCII para su posterior procesamiento estadístico.

2.5Regresión logística

Después del proceso de selección de las variables explicativas se debe realizar un conjunto de ajustes en las variables del modelo, debido a su diferente naturaleza de medición. Por una parte, existen variables cuantitativas con diferente unidad de medida y, por otra parte, variables categóricas compuestas por un determinado conjunto de clases. La solución al primer inconveniente consiste en normalizar todos los valores en una unidad de medición común (Nefeslioglu et al., 2008). La solución tradicional al segundo problema es crear variables binarias o dicotómicas para cada una de las diferentes clases (Guzzetti et al., 1999). Sin embargo, en el caso de que existan muchos parámetros, como es el caso de la variable TMS en el presente estudio, la función lineal resultante sería muy larga, su cálculo muy complejo y la evaluación estadística de los resultados de la regresión final para cada variable independiente puede presentar errores de interpretación y multicolinealidad (Ayalew y Yamagishi, 2005).

Por estas razones, en el presente estudio se optó por un enfoque basado en la normalización de los valores de las variables cuantitativas (Choi et al., 2010):

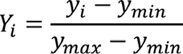(E.1)

donde Y1 en la Ecuación 1 corresponde a los valores normalizados ymin y ymax que representan los valores mínimos y máximos de y1 respectivamente. Como consecuencia, las variables tomarán valores en el rango [0,1].

Con respecto a las variables cualitativas, se procedió a mantener la variable uso del suelo como variable categórica y convertir la variable TMS en cuantitativa mediante el cálculo de las densidades de los puntos de erosión para cada una de las clases que compone dicha variable (Ayalew y Yamagishi, 2005).

La variable dependiente categórica dicotómica se estableció asignando el valor 1 en una tabla de atributos vinculada al archivo de puntos y creada a partir de los procesos de erosión identificados. El valor 0 se asignó a un conjunto de puntos aleatorios distribuidos uniformemente dentro del área de estudio, que no deben coincidir espacialmente con los procesos de erosión y cuya cantidad debe de ser similar a estos últimos. En este estudio los valores de los coeficientes estimados de la función de regresión logística y los estadísticos anexos fueron calculados mediante el programa IBM SPSS Statistics 21.

Los mapas de susceptibilidad de erosión fueron generados a en el entorno de ArcGIS 10.2, mediante una interpolación, según el método de distancia inversa ponderada a partir de los valores pronosticados por regresión logística y asignados en una tabla de atributos perteneciente al archivo de puntos de presencia y ausencia de erosión. Los valores fueron clasificados, según los siguientes rangos: Muy baja (0-0.30), baja (0.31-0.50), moderada (0.51-0.60), alta (0.61-0.70) y muy alta (0.71-1.00).

2.6Redes neuronales artificiales

El modelo de redes neuronales artificiales se ejecutó en el programa R 3.4.3 (R Core Team, 2017) mediante el paquete neuralnet (Fritsch y Günther, 2008), el cual incluye un conjunto de algoritmos, entre ellos el de retropropagación tradicional (backpropagation) y el retropropagación resiliente (resilient backpropagation). El primero es el que más comúnmente ha sido empleado, aunque más recientemente se está imponiendo el uso del segundo, por resultar, significativamente, más rápido y eficiente (Gómez-Ossa y Botero-Fernández, 2017; Günther y Fritsch, 2010). La diferencia entre ambos algoritmos se basa en que el resiliente no utiliza la magnitud del gradiente para determinar el cambio de los pesos, sino el signo del gradiente. En segundo lugar, no utiliza una tasa de entrenamiento global para el ajuste de todos los pesos y sesgos, sino que calcula tasas de cambio para cada peso y sesgo de forma independiente (Bailey, 2015). En el presente estudio se realizó un análisis exploratorio utilizando ambos algoritmos y combinando estructuras diferentes. Además de confirmar una mayor rapidez y eficiencia en la convergencia de la red, el desempeño en términos de su capacidad de pronóstico de la variable dependiente fue, significativamente, superior con el algoritmo de retropropagación resiliente.

Este paquete ejecuta el entrenamiento de una red neuronal mediante el método batch, a partir de un conjunto finito de variables de entrada y una variable dependiente, en este caso dicotómica, que es la que se pretende estimar. A partir de la selección del algoritmo, neuralnet permite la selección de una forma flexible, tanto del número de capas ocultas como de la cantidad de neuronas ocultas de acuerdo con los requisitos de complejidad que se asigne el usuario (Günther y Fritsch, 2010).

El funcionamiento de una red neural precisa de la partición de los datos en una muestra aleatoria de entrenamiento y otra de prueba. La muestra de entrenamiento comprende los registros de datos utilizados para entrenar la red neuronal. La muestra de prueba es un conjunto independiente de registros de datos que se utiliza para realizar un seguimiento de los errores durante el entrenamiento, con el fin de evitar un sobreajuste. El porcentaje de distribución finalmente asignado al algoritmo fue de un 70 % de entrenamiento y de un 30 % de prueba, se introdujo una variable de partición que genera números aleatorios, para volver a crear con exactitud las muestras utilizadas en el análisis.

Aunque el algoritmo no requiere que las variables de entrada estén linealmente relacionadas, es conveniente que las variables continuas sean normalizadas con el propósito de que la red neuronal asigne la misma importancia a los datos (Nefeslioglu et al., 2008), para lo cual se empleó la Ecuación 1. Las variables de naturaleza cualitativa (uso del suelo y TMS) se convirtieron en numéricas mediante el cálculo de las densidades de los puntos de erosión para cada una de las clases que compone dicha variable (Ayalew y Yamagishi, 2005).

En el diseño de la arquitectura de la red se seleccionó la ecuación sigmoide como función de activación de la capa de salida, lo cual permite obtener valores de estimación comprendidos en el intervalo [0,1], de manera que puedan compararse con los resultados obtenidos en la regresión logística.

La variable dependiente, al igual que en la regresión logística, es dicotómica (erosión/no erosión). Para evaluar el nivel de predicción de la red neuronal se entrenaron ocho configuraciones distintas que modifican solamente el número de neuronas de la capa oculta. La etapa de entrenamiento finaliza en el momento en que el error alcanza un valor umbral predefinido en el paquete neuralnet igual a 0.01 (Günther y Fritsch, 2010). En ese proceso, las ponderaciones de cada factor se modifican de forma iterativa hasta alcanzar un valor óptimo de convergencia. Se introdujo en el script el algoritmo de Garson (1991), el cual permite visualizar los valores de estas ponderaciones que representan la importancia relativa de cada factor en valor absoluto (Beck, 2018).

Los mapas finales de susceptibilidad de erosión se crearon en ArcGIS 10.2, por medio de una interpolación en la que se aplicó el método de distancia inversa ponderada. Con el objetivo de poder hacer comparaciones espaciales, los valores de los mapas fueron clasificados de la misma forma que en la regresión logística.

2.7Validación de resultados

En el presente estudio se verificaron sendos modelos de regresión logística y redes neuronales artificiales por el método de característica operativa del receptor (ROC, en sus siglas en inglés). La función ROC calcula la proporción de positivos pronosticados de forma correcta (sensibilidad) contra la proporción de negativos pronosticados erróneamente (1-especificidad) para todas las posibles combinaciones de umbrales de discriminación entre ambos resultados (Swets, 1988). El área debajo de la curva ROC (AUC, en sus siglas en inglés) representa la calidad de un sistema de pronóstico, pues describe la capacidad del sistema para predecir correctamente la ocurrencia o no de un evento predefinido (Pontius y Schneider, 2001; Swets, 1988). Sus valores varían en un rango de 0.50 a 1.00, por lo que cuanto más se aproximen a 1.00, mejor será la calidad del pronóstico.

Dado que el presente estudio, cuyos resultados se representan en forma de mapas, incorpora un análisis comparativo de dos modelos de predicción, es conveniente analizar la correspondencia espacial entre ambos. Tomando como mapa de referencia aquel que logre una mayor precisión, se pretende conocer en qué grado el segundo se aproxima a las características del primero. Para ello los mapas se clasifican previamente en categorías iguales y se comparan por medio de una tabla de contingencia, cuyas celdas contienen el número de pixeles correspondientes. Por medio del programa IDRISI 17.02 Selva (http://www.clarklabs.org/) (Eastman, 2012) se calcularon los coeficientes chi-cuadrado, V de Cramer y el índice Kappa (Cohen, 1960). En relación con este último es necesario precisar que, en realidad, este índice captura solamente el grado de correspondencia cuantitativa total por categorías y no en términos de localización espacial y, por lo tanto, no distingue entre el error cuantitativo y el error de localización (Pontius, 2000).

2.8Análisis de incertidumbre

Las posibles fuentes de incertidumbre se encuadran en las siguientes categorías: (1) contexto y marco del modelo, (2) inputs o atributos del modelo, (3) parámetros del modelo, (4) estructura del modelo y (5) soporte técnico del modelo (Refsgaard et al., 2007). En el presente estudio se abordó un análisis cuantitativo de la variabilidad del índice de susceptibilidad de erosión, por considerarse como imprecisos o aleatorios los valores de los atributos uso y coberturas del suelo y el índice NDVI.

El mapa de usos y coberturas del suelo se elaboró mediante la digitalización de polígonos a partir de la interpretación de una imagen de Google Maps a escala 1:5 000. Se midió el grado de precisión del mapa resultante comparándose con una imagen de Google Earth a partir de los resultados de una muestra aleatoria de observaciones; estos resultados se estructuraron en una matriz de confusión. Se calculó la proporción total de aciertos (Congalton, 1991) y se registró la principal fuente de error en la identificación de las tres clases de bosque. Por este motivo, para la definición de la variable aleatoria en el modelo de incertidumbre, se estableció un error máximo del 20 % en la asignación de las tres diferentes categorías de bosque (natural, secundario e intervenido). Una clasificación supervisada por medio del método de máxima verisimilitud suele presentar un error del 20 % (Liu et al., 2007).

El cálculo del índice de vegetación NDVI requiere de la selección previa del satélite, el cual presenta diferencias significativas en las resoluciones espacial, temporal, espectral y radiométrica (Weber et al., 2008) que se proyectarán posteriormente en los valores del índice NDVI (Brown et al., 2006). Se calculó el índice NDVI en las imágenes de satélite disponibles en los años 2014 y 2015 y se encontraron diferencias en su distribución. Se calcularon números aleatorios asignándose una distribución de probabilidad de valores extremos o de Gumbel (desviación estándar del 10 %).

La variabilidad conjunta del índice de susceptibilidad de erosión se cuantificó en el modelo de regresión logística mediante una simulación de Monte Carlo (10 000 simulaciones) en el programa Oracle Crystal Ball 11.1.

3.Resultados

3.1Inventario de procesos de erosión

Se registraron un total de 604 eventos genéricos de erosión, cuya distribución espacial a lo largo de la subcuenca del Río Claro se muestra en la Figura 2.

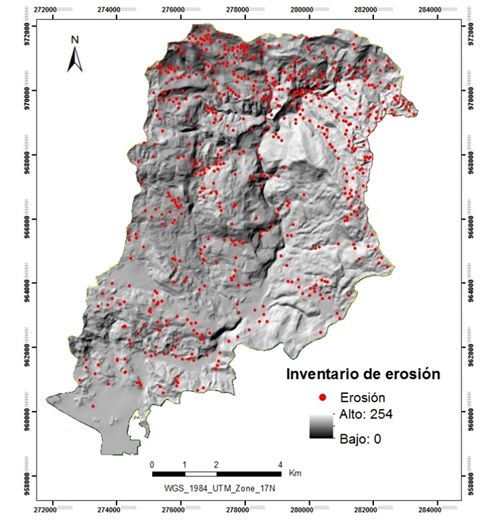
Figura 2. Inventario de los procesos de erosión observables en la subcuenca del Río Claro.
Figure 2. Erosion inventory and location map of the Claro river sub-basin.

Cuadro 1. Porcentaje del área para cada clase de usos y coberturas del suelo.
Table 1. Percentage of the area for each land use class.

Uso del suelo	Área (%)
Bosque intervenido	4.73
Bosque natural	40.54
Bosque secundario	13.17
Charral/tacotal	6.91
Cuerpo de agua	1.27
Cultivo anual	0.60
Palma de aceite	1.11
Pasto	21.76
Plantación forestal	7.96
Urbano	1.75

Figura 3. Mapas de factores condicionantes: (a) Uso y cobertura del suelo; (b) elevación, (c) pendiente, (d) índice de vegetación diferencial diferenciado, (e) distancia euclidiana a cauces, (f) densidad del factor subunidades geomorfológicas del terreno.
Figure 3. Thematic maps of the study area: (a) Land use, (b) Elevation, (c) slope angle, (d) NDVI, (e) drainage density networks, (f) terrain mapping subunits (geomorphology).

3.2Regresión logística

Los resultados del modelo de regresión logística se resumen en el Cuadro 2. Los valores de los coeficientes correspondientes a las categorías del uso del suelo deben interpretarse con relación con la categoría de referencia que en este caso se corresponde a bosque natural. Todas ellas resultaron estadísticamente significativas, salvo las de plantación forestal y bosque secundario. Para evaluar el poder de significancia de los coeficientes de las variables independientes, se aplicó la prueba de Wald (Cuadro 2). De acuerdo con los resultados estadísticos de esta prueba, el uso del suelo correspondiente a pasto resultó ser la categoría estadísticamente más significativa seguida de la de charral/tacotal. Con respecto al resto de las variables, el índice NDVI también resultó ser una variable con un alto grado de significancia estadística y se observa una alta correlación negativa con los valores pronosticados de susceptibilidad de erosión. La variable subunidades geomorfológicas del terreno (TMS) también presentó una alta significancia estadística, superior a las variables pendiente y distancia a la red de drenaje, ambas estadísticamente significativas. El mapa resultante de susceptibilidad de erosión se muestra en la Figura 4a.

Cuadro 2. Coeficientes del modelo de regresión logística, estadístico Wald y nivel de significancia.
Table 2. Logistic regression coefficients, Wald test statistics and significance level.

Categoría	B	E.T.	Wald	gl	Sig.	Exp (B)
Uso del suelo			108.578	7	0.000
Uso (cultivo anual)	3.514	0.633	30.787	1	0.000	33.589
Uso (pasto)	1.583	0.199	63.082	1	0.000	4.868
Uso (charral/tacotal)	1.843	0.266	47.927	1	0.000	6.313
Uso (plantación forestal)	1.088	0.320	11.533	1	0.001	2.967
Uso (bosque secundario)	0.173	0.244	0.499	1	0.480	1.188
Uso (bosque intervenido)	0.424	0.323	1.730	1	0.188	1.529
Uso (palma de aceite)	1.441	0.698	4.261	1	0.039	4.224
TMS	3.705	0.543	46.562	1	0.000	40.634
Distancia red de drenaje	-2.567	0.883	8.454	1	0.004	.077
Pendiente	1.140	0.488	5.469	1	0.019	3.128
NDVI	-5.426	0.740	53.812	1	0.000	.004
Constante	2.949	0.643	21.034	1	0.000	19.087

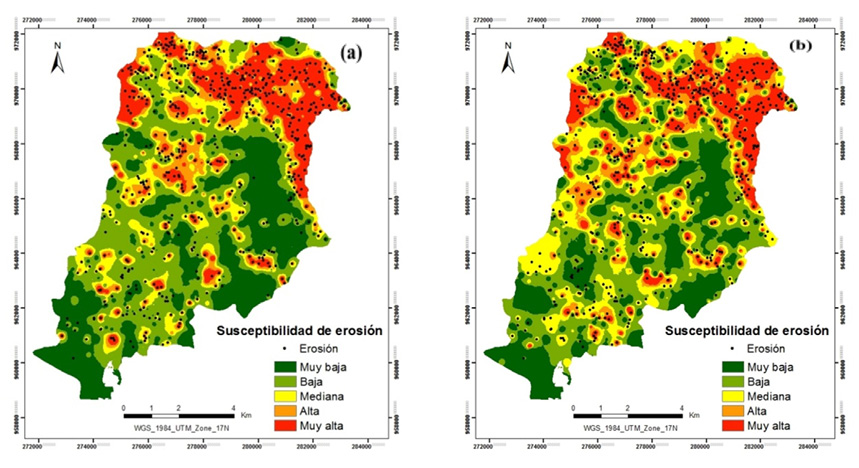
Figura 4. Mapas de susceptibilidad de erosión mediante los métodos: (a) regresión logística y (b) redes neuronales artificiales.
Figure 4. Erosion susceptibility maps produced by (a) logistic regression and (b) artificial neural networks.

El Cuadro 3 muestra el porcentaje del área total de extensión de cada una de las 5 categorías de clasificación del índice de susceptibilidad de erosión. Los valores más altos se localizan geográficamente en la parte alta de la subcuenca, especialmente en la intersección de la Fila Cruces y la Fila Zapote, en un rango de altitud comprendido entre los 1 000 y 1 600 m s.n.m.

Cuadro 3. Porcentaje del área cubierta según los niveles de clasificación de susceptibilidad de erosión.
Table 3. Percentage of the area covered by each of the erosion susceptibility classification levels.

Rango de probabilidad	Clasificación	Área (log*) (%)	Área (red**) (%)
0.01 – 0.30	Muy baja	0.27	0.22
0.31 – 0.50	Baja	0.32	0.29
0.51 – 0.60	Moderada	0.13	0.20
0.61 – 0.70	Alta	0.10	0.11
0.71 – 0.99	Muy alta	0.17	0.16

*Método de regresión logística.

**Método de redes neuronales artificiales.

3.3Redes neuronales artificiales

Los resultados de las redes neuronales artificiales entrenadas mediante el algoritmo de retropropagación resiliente se muestran en el Cuadro 4. Se incluyen un conjunto de indicadores que evalúan la calidad y la bondad de ajuste de los resultados de la estimación realizada. El término error se refiere a la proporción del total de valores de la muestra pronosticados de forma incorrecta por la red neuronal. El criterio de información de Akaike (AIC, en sus siglas en inglés) es un estadístico que mide la bondad de ajuste de la estimación que se calcula a partir del valor máximo de la función de verosimilitud y dado un conjunto de modelos estimados, el preferido será aquel con valor mínimo (Akaike, 1973). El criterio de información bayesiano (BIC, en sus siglas en inglés) es otro estimador de la bondad de ajuste similar al AIC, también directamente relacionado con el máximo valor de la función de verosimilitud y, dados dos modelos con el mismo número de variables explicativas, se preferirá el de menor valor (Schwarz, 1978).

Los resultados presentaron valores en sus indicadores que evidencian un alto desempeño de la red neuronal. Los resultados confirmaron que, en general, tanto los valores del error como de AUC, mejoran su registro cuando se incrementa el número de neuronas ocultas hasta alcanzar un umbral de veinte. En cuanto a los valores registrados del AIC, confirman la tendencia esperada de disminuir conforme descienden los valores del error.

Cuadro 4. Resultados de la capacidad predictiva de ocho corridas de la red neuronal para diferente número de capas ocultas, valor del área bajo la curva y estadístico AIC.
Table 4. Results of eight times running the resilient back-propagation network model for selection of the number of hidden neurons, area under ROC curve (AUC) and AIC statistic.

Red	Número de neuronas ocultas	Error	Validación AUC	AIC
1	5	0.2187	0.8582	771.27
2	6	0.2013	0.8589	761.22
3	10	0.1970	0.8687	783.44
4	12	0.1883	0.8820	724.79
5	15	0.1614	0.8929	705.56
6	18	0.1657	0.8880	691.73
7	20	0.1657	0.8907	662.72
8	22	0.1718	0.8923	695.35

La red neuronal compuesta por veinte neuronas ocultas fue corrida un total de diez veces modificándose los valores de la muestra aleatoria por el algoritmo. Los resultados de las ponderaciones de cada factor en valor se muestran en el Cuadro 5. Los valores más altos corresponden a la variable subunidades geomorfológicas del terreno (TMS) y la distancia euclidiana a la red de drenaje, según la corrida y, en tercer lugar, la variable uso del suelo.

Cuadro 5. Ponderaciones de cada factor en la red neuronal seleccionada.
Table 5. Weights derived from ANN estimation model from ten samples.

Variable	1	2	3	4	5	6	7	8	9	10
Uso del suelo	0.134	0.178	0.117	0.158	0.122	0.142	0.149	0.193	0.136	0.191
TMS	0.315	0.324	0.275	0.259	0.242	0.374	0.246	0.283	0.337	0.236
NDVI	0.140	0.063	0.157	0.085	0.134	0.138	0.106	0.123	0.115	0.135
Distancia a la red de drenaje	0.252	0.285	0.295	0.353	0.268	0.241	0.313	0.275	0.299	0.306
Pendiente	0.158	0.151	0.155	0.145	0.233	0.105	0.186	0.127	0.112	0.131
AUC	0.901	0.898	0.908	0.898	0.885	0.911	0.903	0.906	0.903	0.907

El mapa resultante de susceptibilidad de erosión (Figura 4b) se elaboró a partir de los valores estimados de la variable dependiente seleccionando la red neuronal que presentó el mejor desempeño. Los valores se exportaron en formato ASCII al programa ArcGIS 10.2 para su posterior representación espacial.

3.4Validación de los modelos de susceptibilidad

En el Cuadro 4 se muestran los resultados de la predicción de la probabilidad de ocurrencia de procesos de erosión mediante redes neuronales artificiales donde se incluyen los valores del área debajo de la curva ROC para cada una de las redes entrenadas. Se puede comprobar que los valores de este indicador aumentan conforme se incrementa el número de neuronas ocultas hasta alcanzar un valor umbral de veinte.

En el modelo de regresión logística, el valor del área debajo de la curva ROC obtenido fue 0.821. Estos resultados evidencian, en general, un alto nivel de predicción para ambos modelos, con mejores resultados mediante el modelo de redes neuronales.

Con respecto a la medición del grado de correspondencia espacial entre los dos modelos, los resultados se resumen en el Cuadro 6. El valor obtenido en la prueba Chi-cuadrado supone aceptar la hipótesis de dependencia o concordancia entre los resultados de los dos modelos. El coeficiente V de Cramer presenta un valor moderado y el coeficiente de Kappa un valor sustancial, según la clasificación de Landis y Koch (1977). Como consecuencia, según estos indicadores, el mapa obtenido mediante el modelo de regresión logística presentaría un grado de concordancia espacial moderado en comparación con el generado mediante redes neuronales artificiales, por lo tanto, el primer modelo sería, en este caso, insuficientemente robusto como método alternativo al segundo.

Cuadro 6. Estadísticos de correspondencia espacial, Kappa estándar, V de Cramer y chi cuadrado.
Table 6. Standard Kappa index of agreement, Cramer’V and Chi square spatial accuracy statistics.

Estadístico	Valor
Chi cuadrado	3000726.00
V de Cramer	0.6229
Kappa (categoría ISE muy baja)	0.7389
Kappa (categoría ISE baja)	0.4489
Kappa (categoría ISE mediana)	0.2144
Kappa (categoría ISE alta)	0.2679
Kappa (categoría ISE muy alta)	0.6798
Kappa estándar total	0.6534

ISE: Índice de susceptibilidad de erosión.

3.5Análisis de incertidumbre

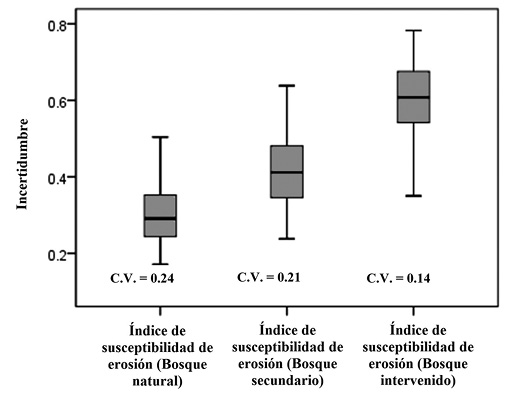
El efecto de la incertidumbre existente en las variables explicativas del modelo de regresión logística, uso y cobertura del suelo, y el índice NDVI, sobre el índice de susceptibilidad de erosión se muestra en la Figura 5. El diagrama de cajas refleja el rango de variabilidad del índice, según la clase de cobertura boscosa (natural, secundario e intervenido). Las diferencias en los rangos intercuartílicos (Q3-Q1) son similares entre las clases de cobertura boscosa. Los valores promedio reflejan las diferencias relativas con los valores promedio zonales, según las diferentes categorías de uso y coberturas del suelo (Cuadro 7).

Figura 5. Diagrama de cajas de la incertidumbre en el índice de susceptibilidad de erosión según tres tipos de cobertura boscosa. Se incluye el valor del coeficiente de variación (C.V.).
Figure 5. Box-plots describing differences in uncertainty values of the erosion susceptibility index between three forested cover classes. A coefficient of variation (C.V.) is given for each box-plot.

Cuadro 7. Parámetros estadísticos descriptivos del índice de susceptibilidad de erosión (método de redes neuronales) según la categoría de uso y cobertura del suelo correspondiente.
Table 7. Descriptive statistic parameters of the erosion susceptibility index between land-use classes.

Uso del suelo	Media	Desviación estándar	Coeficiente de variación
Bosque intervenido	0.59	0.1769	0.2998
Bosque natural	0.42	0.1882	0.4480
Bosque secundario	0.47	0.2128	0.4527
Charral/tacotal	0.54	0.1818	0.3366
Cultivo anual	0.53	0.1279	0.2413
Palma de aceite (Elais guineensis)	0.39	0.1275	0.3269
Pasto	0.60	0.1937	0.3228
Plantación forestal de melina (Gmelina arborea)	0.41	0.1447	0.3529

4.Discusión

El primer desafío que presenta este estudio se centra en la correcta identificación espacial de los procesos de erosión a partir de la resolución espectral y radiométrica de las imágenes de los sensores remotos. Además de la interpretación espacial, se requiere de una rigurosa verificación de campo. Sin embargo, la complejidad topográfica del terreno, el difícil acceso y la densa vegetación dificultaron esta labor. Como consecuencia, este proceso encierra un nivel de incertidumbre que debe tenerse en cuenta. Al respecto, para minimizar este problema, es conveniente disponer de un conjunto de imágenes pasadas con el propósito de identificar patrones generales de distribución espacial de los eventos de erosión. En el presente estudio se utilizaron en ese sentido fotografías aéreas correspondientes al Proyecto CARTA (2005).

En segundo lugar, la precisión del modelo de predicción va a depender de la disponibilidad de información sobre los factores condicionantes, así como de su calidad y resolución espacial. En este caso, el área de estudio presenta el inconveniente de albergar escasos estudios científicos. Por este motivo no fue posible disponer de datos, por ejemplo, sobre litología, una de las variables explicativas imprescindibles en los estudios de susceptibilidad de deslizamientos. A pesar de este inconveniente, las variables explicativas incorporadas en este estudio presentan una escala y una resolución espacial que otorgan robustez y precisión a los modelos de predicción.

En este estudio se aplicó el criterio según el cual los análisis de susceptibilidad deben incorporar, exclusivamente, factores condicionantes a diferencia de los análisis de amenazas (hazard) que incluyen, además, factores activadores como precipitación o sismicidad (Van Westen et al., 2003). Este criterio se basa en el concepto de susceptibilidad que, aplicado a los deslizamientos, ha sido definido como la probabilidad relativa de ocurrencia de estos eventos en un área determinada como consecuencia de la influencia exclusiva de factores intrínsecos (Dai et al., 2001). Sin embargo, existen estudios recientes que abordan análisis de susceptibilidad que incorporan factores activadores o extrínsecos como precipitaciones o sismicidad (Chen et al., 2017; Dou et al., 2015).

El otro aspecto esencial que determina la robustez y precisión de los modelos de susceptibilidad es la elección del método de predicción o algoritmo. Los resultados generales obtenidos en este estudio, tanto en el modelo de regresión logística como en el de redes neuronales artificiales, mostraron un grado de predicción general elevado, aunque ligeramente por debajo del alcanzado en otros estudios (Elkadiri et al., 2014; Nefeslioglu et al., 2008; Pradhan y Lee, 2010), donde el nivel de predicción alcanzado en sus modelos supera el 90 %.

Los mapas de susceptibilidad obtenidos a partir de los resultados pronosticados por los dos modelos presentan diferencias en cuanto a la distribución espacial de las diferentes categorías de clasificación. El grado de concordancia espacial total definido por el coeficiente de Kappa estándar es del 65 %, similar al que se presenta en Kalantar et al., (2018) e inferior al 91.5 % en Elkadiri et al., (2014) para los mismos modelos. La explicación a esta diferencia puede deberse, entre otros posibles factores, a las diferencias existentes en la importancia relativa de las variables explicativas entre los dos modelos, como se muestra en los Cuadros 2 y 5. Estas diferencias también se manifiestan en Ngadisih et al., (2016) y Lee et al., (2016).

La mayoría de los estudios de susceptibilidad no incorporan un análisis de incertidumbre, a pesar de que los datos, dada su naturaleza, pueden ser altamente susceptibles de presentar imprecisiones o aleatoriedad. Admitiendo que un análisis de incertidumbre integral puede llegar a ser complejo, se considera que es relevante plantear, al menos, un análisis parcial que incorpore alguna de las posibles fuentes de incertidumbre y, de esta manera, cuantificar, desde determinados supuestos, el grado de variabilidad de los valores pronosticados.

5.Conclusiones

En el presente estudio se realizó un análisis de susceptibilidad a partir de un inventario de procesos de erosión de cualquier clase, con el propósito de generar una zonificación espacial que registrara el grado de vulnerabilidad integral de la subcuenca del Río Claro como consecuencia del efecto de un conjunto de factores intrínsecos. El hecho de no existir un criterio unánime en la selección de los factores condicionantes y el empleo de modelos probabilísticos posibilita la robustez de este estudio.

Para ello, se han empleado comparativamente dos modelos de predicción, regresión logística y redes neuronales artificiales. Este último presentó una mayor capacidad predictiva en términos de la función ROC, resultado que comparten la mayoría de estudios (Nefeslioglu et al., 2008; Ngadisih, et al., 2016; Pradhan y Lee, 2010). Esta evidencia empírica, unida al hecho de que el segundo modelo es un método no-paramétrico y que, por tanto, permite flexibilizar determinados supuestos de partida con respecto a las variables explicativas, fortalece su prevalencia sobre el modelo de regresión logística.

Los mapas de susceptibilidad de erosión muestran una elevada alteración ecológica del ecosistema en términos de la probabilidad de ocurrencia de eventos de erosión, especialmente en la parte alta de la subcuenca. El estudio evidencia que el cambio del uso del suelo, en términos del establecimiento de fincas de ganadería extensiva en terrenos de aptitud forestal y alta pendiente, es el factor más relevante. Como consecuencia, se propone la introducción de proyectos de reforestación que posibiliten la reducción de la vulnerabilidad del terreno, el riesgo de amenazas sobre la población, la restauración progresiva de los servicios ecosistémicos y el incremento de la resiliencia ambiental.

6.Ética y conflicto de intereses

Las personas autoras declaran que han cumplido totalmente con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en la producción del manuscrito; que no hay conflictos de intereses de ningún tipo; que todas las fuentes financieras se mencionan completa y claramente en la sección de agradecimientos; y que están totalmente de acuerdo con la versión final editada del artículo.

7.Agradecimientos

El equipo de investigación agradece, al Programa de Becas CeNAT-CONARE, por el apoyo financiero; así como al personal del laboratorio PRIAS del Centro Nacional de Alta Tecnología (CeNAT), por la colaboración técnica y logística. A la Revista y personas revisoras anónimas, por los comentarios realizados, los cuales ayudaron a mejorar el escrito.

8.Referencias

Akaike, H. (1973). Information Theory as an Extension of the Maximum Likelihood principle. In N. Petrov y F. Csaki (Eds.), Second International Symposium on Information theory (pp. 267-81). Akademiai Kiado.

Ayalew, L. y Yamagishi, H. (2005). The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology, 65, 15–31. https://doi.org/10.1016/j.geomorph.2004.06.010.

Bailey, T. M. (2015). Convergence of Rprop and variants. Neurocomputing, 159, 90-95. https://doi.org/10.1016/j.neucom.2015.02.016

Bayard, B., Curtis, M. J. y Shannon, D. (2006). The Adoption and Management of Soil Conservation Practices in Haiti: The Case of Rock Walls. Agricultural Economics Review, 2, 28-39. http://doi.org/10.22004/ag.econ.44111.

Beck, M. W. (2018). NeuralNetTools: Visualization and Analysis Tools for Neural Networks. Journal of Statistical Software, 85, 11, 1-20. http://doi.org/10.18637/jss.v085.i11.

Brown, E. M., Pinzón, J. E. Didan, K., Morisette, J. T. y Tucker, C. J. (2006). Evaluation of the Consistency of Long-Term NDVI Time Series Derived From AVHRR, SPOT-Vegetation, SeaWiFS, MODIS, and Landsat ETM+ Sensors. IEEE Transactions on Geoscience and Remote Sensing, 44(7), 1787-1793. https://doi.org/10.1109/TGRS.2005.860205.

Bruijnzeel, L. A. (2004). Hydrological functions of tropical forests: not seeing the soil for the trees? Agriculture, Ecosystems and the Environment, 104, 185-228. https://doi.org/10.1016/j.agee.2004.01.015

Chandler, G., Markham, B. L. y Helder, D. L. (2009). Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sensing of Environment, 113, 893-903. https://doi.org/10.1016/j.rse.2009.01.007.

Chen, W., Xie, X., Peng, J., Wang, J., Duan, Z. y Hong, H. (2017) GIS-based landslide susceptibility modelling: a comparative assessment of kernel logistic regression, Naïve-Bayes tree, and alternating decision tree models, Geomatics, Natural Hazards and Risk, 8(2), 950-973. https://doi.org/10.1080/19475705.2017.1289250.

Choi, J., Oh, H. J., Won, J. S., y Lee, S. (2010). Validation of artificial neural network model for landslide susceptibility mapping. Environmental Earth Sciences, 60, 473-483. https://doi.org/10.1007/s12665-009-0188-0.

Chung C.J. y Fabbri A. G. (1993). The representation of geoscience information for data integration. Non-renewable Resources, 2, 122–139. https://doi.org/10.1007/BF02272809

Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20(1), 37-46. https://doi.org/10.1177/001316446002000104.

Congalton, R. G. (1991). A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sensing of Environment, 37, 35-46. https://doi.org/10.1016/0034-4257(91)90048-B.

Cortés, J. (1990). The coral reefs of Golfo Dulce, Costa Rica. Distribution and community Structure. National Museum of Natural History. Smithsonian Institution. Atoll Research Bulletin, 344.

Dai, F. C., Lee, C. F., Li, J. y Xu, Z. W. (2001). Assessment of landslide susceptibility on the natural terrain of Lantau Island, Hong Kong. Environmental Geology, 40, 381–391. https://doi.org/10.1007/s002540000163.

Dou, J., Paudel, U., Oguchi, T., Uchiyama, S. y Hayakawa, Y. S. (2015). Shallow and Deep-Seated Landslide Differentiation Using Support Vector Machines: A Case Study of the Chuetsu Area, Japan. Terrestrial Atmospheric and Oceanic Sciences, 26(2), 227-239. http://doi.org/10.3319/TAO.2014.12.02.07(EOSI).

Fritsch, S. y Günther, F. (2008). Neuralnet: Training of Neural Networks. R Foundation for Statistical Computing. https://doi.org/10.32614/RJ-2010-006

Funtowicz, S. O. y Ravetz, J. R. (1990). Uncertainty and Quality in Science for Policy. Kluwer Academic Publishers. https://doi.org/10.1007/978-94-009-0621-1_3
https://doi.org/10.1007/978-94-009-0621-1

Garson, G. D. (1991). Interpreting Neural Network Connection Weights. Artificial Intelligence Expert, 6(4), 46–51.

Gómez-Ossa, L. F., y Botero-Fernández, V. (2017). Desempeño de redes neuronales artificiales en la modelación de la deforestación en una región tropical de Colombia. En J-F. Mas (Comp.), Análisis y modelación de patrones y procesos de cambio. Centro de Investigaciones en Geografía Ambiental, UNAM.

Günther, F. y Fritsch, S. (2010). Neuralnet: Training of Neural Networks. The R Journal, 2(1). https://doi.org/10.32614/RJ-2010-006

Guzzetti, F., Carrara, A., Cardinali, M. y Reichenbach, P. (1999). Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology, 31, 181–216. https://doi.org/10.1016/S0169-555X(99)00078-1.

Hamel, P. y Bryant, B. P. (2017). Uncertainty assessment in ecosystem services analyses: Seven challenges and practical responses. Ecosystem Services, 24, 1–15. http://doi.org/10.1016/ j.ecoser.2016.12.008.

Kalantar, B., Pradhan, B., Naghibi, S.A., Alireza Motevalli, A. y Mansor, S. (2018). Assessment of the effects of training data selection on the landslide susceptibility mapping: a comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN), Geomatics, Natural Hazards and Risk, 9(1), 49-69. http://doi.org/10.1080/19475705.2017.1407368.

Landis, J. y Koch, G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33, 159-74. https://doi.org/10.2307/2529310

Lee, S., Jeon, S. W., Kwan-Young, O. y Moung-Jin, L. (2016). The spatial prediction of landslide susceptibility applying artificial neural network and logistic regression models: A case study of Inje, Korea. Open Geosciences, 8(1), 117-132. https://doi.org/10.1515/geo-2016-0010.

Liu, C. R., Frazier, P. y Kumar, L. (2007). Comparative assessment of the measures of thematic classification accuracy. Remote Sensing of Environment, 107, 606–616. https://doi.org/10.1016/j.rse.2006.10.010.

Mende, A. y Astorga, A. (2007). Incorporating geology and geomorphology in land management decisions in developing countries: A case study in Southern Costa Rica. Geomorphology 87, 68–89. https://doi.org/10.1016/j.geomorph.2006.06.043.

MINAE-CENIGA. (1998). Información cartográfica de la misión TERRA-Costa Rica. Ministerio de Ambiente, Energía y Minas.

Nefeslioglu, H. A., Gokceoglu, C., y Sonmez, H. (2008). An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Engineering Geology, 97, 171–191. http://doi.org/10.1016/j.enggeo.2008.01.004.

Ngadisih, Bhandary, N. P., Yatabe, R. y Dahal, R. K. (2016). Logistic regression and artificial neural network models for mapping of regional-scale landslide susceptibility in volcanic mountains of West Java (Indonesia). American Institute of Physics Conference Proceedings, 1730, 060001-1–060001-11. http://doi.org/10.1063/1.4947407.

Pontius, R. G., Jr. (2000). Quantification error versus location error in the comparison of categorical maps. Photogrammetric Engineering and Remote Sensing, 66, 1011–1016.

Pontius, R. G., Jr. y Schneider, L. C. (2001). Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agriculture, Ecosystems and Environment, 85, 239–248. http://doi.org/10.1016/S0167-8809(01)00187-6.

Pradhan, B. (2013). A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Computers & Geosciences, 51, 350-365. https://doi.org/10.1016/j.cageo.2012.08.023.

Pradhan, B., y Lee, S. (2010). Regional landslide susceptibility analysis using backpropagation neural network model at Cameron Highland, Malaysia. Landslides, 7(1), 13-30. https://doi.org/10.1007/s10346-009-0183-2.

ProDUS. (2007). Diagnóstico. Plan regulador cantonal de Golfito (Tomo I). Escuela de Ingeniería Civil. Universidad de Costa Rica.

Proyecto CARTA. (2005). Centro Nacional de Alta Tecnología. Consejo Nacional de Rectores (CONARE).

R Core Team. (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. URL https://www.R-project.org/.

Refsgaard, J. C., van der Sluijs, J. P., Højberg, A. L. y Vanrolleghem, P. A. (2007) Uncertainty in the environmental modelling process––a framework and guidance. Environmental Modelling and Software, 22, 1543–1556. http://dx.doi.org/10.1016/j.envsoft.2007.02.004.

Schwarz. G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461–464. https://doi.org/10.1214/aos/1176344136

Steinfeld, H. (2002). Producción animal y el medio ambiente en Centroamérica. . En Intensificación de la ganadería en Centroamérica. Beneficios económicos y ambientales (Cap. I. Ganadería y medio ambiente en Centroamérica. FAO.

Swets, J. A. (1988) Measuring the accuracy of diagnostic systems. Science, 240, 1285–1293. https://doi.org/10.1126/science.3287615

Szott, L., Ibrahim, M. y Beer, J. (2000). The hamburger connection hangover: cattle pasture land degradation and alternative land use in Central America. Serie Técnica. Informe Técnico n.o 313. CATIE.

Van Westen, C. J., Rengers, N. y Soeters, R. (2003). Use of Geomorphological Information in Indirect Landslide Susceptibility Assessment. Natural Hazards, 30, 399–419. https://doi.org/10.1023/B:NHAZ.0000007097.42735.9e.

Weber, K. T., Théau, J., y Serr, K. (2008). Effect of coregistration error on patchy target detection using high-resolution imagery. Remote Sensing of Environment, 112, 845–850. https://doi.org/10.1016/j.rse.2007.06.016.

---