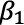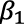Superficie forestal afectada por incendios en México: apuntes iniciales hacia un modelo de manejo preventivo

Forest area affected by fires in Mexico: Initial notes toward a preventive management model

Andrés González-Rosales1, Carlos Francisco Ortiz-Paniagua2

[Recibido: 25 de mayo 2021, Aceptado: 12 de octubre 2021, Corregido: 30 de octubre 2021, Publicado: 1 de enero 2022]

Resumen

[Introducción]: Algunas variables ayudan a explicar la Superficie Forestal Afectada por Incendios (SFAI) que si bien, se conocen intuitivamente, no se han cuantificado para estimar su importancia en la prevención al combate de los incendios forestales. [Objetivo]: plantear un modelo estadístico que demuestre los determinantes de la SFAI y, con ello, aportar información inicial para el fortalecimiento de un esquema para prevención de incendios. [Metodología]: se integraron dos técnicas estadísticas: análisis multivariado de componentes principales y datos panel para entender la relación entre dichas variables intuitivas sobre número de incendios, detección, llegada, temperatura y duración, sobre la SFAI. [Resultados]: sugieren que en 11 entidades federativas de México (Región Centro-Occidente) hay una relación entre la cantidad y duración de incendios, más que proporcional para la cantidad de incendios (1.28) y menos que proporcional para la duración de estos (0.52), en relación con la SFAI. [Conclusiones]: este modelo puede tener aplicaciones en la planificación de acciones y esquemas para la protección de ecosistemas forestales y la asignación de recursos (humanos, equipo y materiales) más eficaz y eficiente a fin de prevenir y reducir los incendios forestales.

Palabras clave: Componentes principales; incendio forestal; Análisis de Datos Panel; Región México Centro-Occidente; superficie forestal.

Abstract

[Introduction]: The Forest Area Affected by Fires (FAAF) could be explained by variables that that although they are intuitively known, they have not been quantified to estimate their importance in preventing the fight of forest fires. [Objective]: To propose a statistical model that demonstrates implicated factors on SAAF and thereby provide initial information for the strengthening of a fire prevention scheme. [Methodology]: Were applied two statistical techniques 1) principal component analysis, was used to justify the variables; and 2) panel data analysis was used to understand the relationship between intuitive variables on detection, arrival, and duration, on the affected surface. [Results]: The results indicate that 11 states of Mexican Central-Western Region there is a relationship between the Quantity and Duration of forest fires, more than proportional for the Quantity of Fires (1.28) and less than proportional with the Duration of these (0.52), in relation to the FAAF. [Conclusions]: This model can have applications in the planning of actions and schemes for the protection and prevention of forest ecosystems and the allocation of resources (human, equipment, and materials) more effective and efficient to prevent and reduce forest fires.

Keywords: Central West México; forest area; forest fire; Panel Data Analysis , Principal Components Analysis.

1. Introducción

Poco más de la quinta parte de los bosques en el mundo se encuentran en América Latina y el Caribe. Estos cubren 49 % de la superficie y representan 57 % de los bosques primarios del mundo, en términos de biodiversidad y conservación (FAO, 2020). América del Sur ha ocupado el primer lugar en incendios forestales entre 2001 y 2018, con una afectación de 597.9 millones de hectáreas (FAO, 2020) Una de las amenazas más importantes a los bosques en América Latina son los incendios forestales que constituyen la principal fuente de transformación de los ecosistemas terrestres, al provocar alteraciones, en su mayoría, negativas como degradación del ecosistema y daños susceptibles de ser valorados económicamente como costos de remediación, de extinción del incendio y de infraestructura (Ocampo Zuleta, 2016).

Entre 2002-2003, se incendió 1.1 % de la superficie de bosques latinoamericanos, aunque 40 % se quemaron solo una vez, para 2018, 48 % de la superficie que padeció incendios ya se había convertido en otros usos. El aumento de la frecuencia de los incendios incrementa los riesgos de pérdida forestal irreversible, transformando los bosques en ecosistemas cada vez más vulnerables a la degradación. Para revertir esta tendencia ante el cambio climático es indispensable implementar acciones clave para conservar los bosques de América Latina (Armenteras et al., 2021). Ante los escenarios más probables de cambio climático es imperante contar con instrumentos para el manejo de los incendios forestales en la región.

Si bien, los incendios forestales forman parte de la naturaleza de los ecosistemas (Pausas, 2020), el presente artículo se refiere a aquellos provocados, directa o indirectamente, que tienen externalidades y consecuencias no deseadas tanto para los ecosistemas como para procesos antrópicos. Se trata de disturbios que ocasionan deforestación, degradación de bosques y pueden disminuir la capacidad de los ecosistemas para la generación de bienes y servicios ecosistémicos (Balvanera, 2012; Rodríguez Trejo, 2015; Urquidi, 2007); es decir, ocasionan un problema de consecuencias trascendentales.

En América Latina, la pérdida de cobertura forestal tras un incendio se estimó en: Panamá (64 %), Paraguay (61 %), Brasil (57 %), México (31 %) Guatemala (30 %) y Belice (17 %) (Armenteras et al., 2021), lo cual transformó el uso del suelo para habilitación de terrenos en actividades económicas. Lo paradójico es que el fuego se usa como herramienta para cambiar el uso forestal por agricultura, ganadería o desarrollo inmobiliario, que enseguida se convierten en demandantes de los servicios ecosistémicos proporcionados por los bosques, como el agua (Rodríguez et al., 2013), situación que, a su vez, aumenta los riesgos de abastecimiento de dichos servicios y se intensifica la deforestación.

Entre 1990 a 2015, mundialmente, se perdieron 178 millones de hectáreas (ha) de bosques (FAO, 2020). Entre 2000 y 2010, la deforestación en México fue de 1 950 000 ha (Programa Nacional de Desarrollo [PND], 2013). Entre 2010 y 2020, se reportaron en promedio 7,5 mil incendios, con una afectación de más de 4.5 millones de hectáreas y, en la región Centro-Occidente, fueron 442 mil ha (Comisión Nacional Forestal [CONAFOR], 2021); causado principalmente por el uso del fuego no controlado, carecer de actividades preventivas y la falta de eficiencia y eficacia en la distribución de los recursos humanos, materiales y equipo para la detección, llegada y combate de los siniestros (Rodríguez, 1996; Rodríguez y Silva & González-Cabán, 2016; Ynouye-Francés et al., 2020).

En el período de 2010 a 2020, se reportaron 53 231 incendios solo en la Región Centro-Occidente, que afectaron 442 mil ha. Entre los lugares más afectados, se encuentran Puebla, Michoacán y el Estado de México, con 68 % del total de la superficie afectada. Los Estados con la mayor cantidad de incendios, históricamente, han sido el Estado de México, Ciudad de México, Chihuahua y Michoacán, acumulando el 52 % de los incendios totales del país en los últimos 20 años (CONAFOR, 2021).

A lo anterior, se le suma la falta de una cultura de prevención de incendios y de labores de presupresión, esenciales para una eficaz liquidación y seguridad en su control (Rodríguez Trejo et al., 2002); el poco apoyo al conocimiento científico, que puede apoyar en la prevención, planeación, la toma de decisión y asignación anual de recursos para atención del sector; además de brindar información sobre la relación entre la Oscilación del Sur (El Niño) y los incendios de México (González-Ramírez et al., 2007; Magaña Rueda et al., 1998; Manzo-Delgado & López-García, 2020).

Dentro de las variables más importantes en torno a este problema, se encuentran: el Número de Incendios Forestales (NIF) y la SFAI; ambas se utilizan para conocer características específicas de los siniestros como: intensidad, largo de llama y velocidad de propagación. También se emplean para conocer la magnitud y daño a la vegetación remanente, por ello su importancia en las estadísticas oficiales, para rendir informes a la sociedad y en las dependencias encargadas (CONAFOR, 2017).

De esta manera, el NIF y la SFAI suelen dar información para las actividades de prevención realizadas como: apertura de brechas cortafuego, líneas negras y quemas prescritas; para con ello detectar áreas de oportunidad sobre las acciones que debieran implementarse (CONAFOR, 2010); a fin de reducir la carga de combustibles y, por lo tanto, la presencia de incendios catastróficos (Loomis et al., 2019). Todo esto en función del combustible presente, el tiempo atmosférico, la topografía del lugar, la pronta detección, el tiempo de llegada al incendio y el tiempo de combate para extinguir el incendio (Pausas, 2020; Rodríguez, 2015).

Tomando como base los estudios referenciados en cuanto a la eficiencia en el combate y las causas de expansión de los incendios forestales, en este estudio se parte de suponer que los factores relativos a la administración para el combate a los incendios se relacionan con la eficacia y eficiencia de las acciones gubernamentales como la detección y llegada para abatir los incendios forestales. Estos aspectos se han estudiado poco en México, de manera que la pregunta conductora se plantea de la siguiente manera: ¿Cómo incidieron las variables: detección (De), tiempo de llegada al incendio (TLI), duración (Dur), temperatura (T) y la ocurrencia o número de incendios forestales (NIF) sobre la SFAI, en las entidades de México?

Las variables De y TLI dependen del personal técnico (torrero); y Dur de las personas brigadistas, los materiales y equipo para combatirlo. Se trata de la eficiencia y la eficacia de las acciones gubernamentales, la cual se expresa en las políticas forestales de protección de los ecosistemas y el combate de los incendios forestales (Rodríguez Trejo, 1994; Rodríguez Trejo, 2015). En este sentido, el proceso administrativo es fundamental para combatir los incendios forestales, lo que se apreciaría bajo la sospecha de que estas variables tendrían una mayor relevancia.

2. Presencia de incendios forestales en México

Los incendios forestales naturales han ocurrido desde siempre, siendo parte de la normalidad del funcionamiento de los ecosistemas. Suele haber tres causas: descargas eléctricas; negligencias, causas incidentales de humanos; y un origen intencionado. El primer caso refiere a causas naturales. En el segundo se trata de quemas que se salen de control, fogatas, fumadores, etc. En el tercero, son los humanos, quienes con diferentes intenciones actúan para incendiar superficies forestales. No obstante, también las condiciones climáticas (temperatura, viento y humedad) y ambientales (disponibilidad de combustible y oxígeno) contribuyen a la magnitud e intensidad de los incendios (Salgado Chávez, 2021) (el triángulo del fuego -oxígeno, temperatura y combustible-).

Un tema preocupante es que las causas de la proliferación por la actividad humana en estas últimas décadas sobrepasan la capacidad de recuperación natural. Con esto, se aprecian cambios en los regímenes de fuego por influencia humana (Cerano-Paredes et al., 2016; Guitian Rivera, 1999; Kauffman, 1991; Parra Lara, 2011; Rodrígues et al., 2004). A la vez, ha crecido el interés, general y regional, la multidisciplinariedad y la investigación sobre las causas, implicaciones y algunos aspectos relacionados con los incendios; tanto en la cantidad de estudios (Harnecker et al., 2020; Rodrígues et al., 2004) como en las técnicas innovadoras desde la inteligencia artificial y sensores remotos para su pronta detección y previsión (Castillo Sarasty, 2021).

En América Latina, y en particular en México, los incendios forestales han sido una preocupación creciente. En la región, se puede apreciar que algunos incendios intencionados buscan cambiar el tipo de cobertura vegetal, usualmente por agricultura, ganadería o desarrollo urbano. Ciertos cultivos que se plantan en lugar de los bosques son los frutales (Schwentesius Rindermann et al., 2021; Macías & Sevilla García, 2021). En otros casos, son incendios que se expandieron más allá de una zona agrícola por descuido y se encuentran también los incendios forestales producto de un descuido humano de turistas o población local (fogatas, quema de basura, cigarro, etc.), lo cual a su vez se relacionan con puntos geográficos de calor, lo que puede ayudar a la prevención de estos (Flores-Garnica et al., 2021).

Para el período 1991 a 2020, la SFAI ha presentado una tendencia creciente a razón de 355 mil ha anuales, si se omite el año 2011 (extraordinario por alcanzar las 956 mil ha), la media disminuye a 315 mil ha anuales, manteniendo una tendencia creciente (Ver Figura 1), la cantidad de incendios anual promedio en México fue de 7,828 para ese periodo. La media estatal la SFAI asciende a 11 mil ha y la cantidad de incendios al año a 245, para el mismo período (Figura 2). Bajo este contexto, se aprecia la importancia que cobra el tema de los incendios forestales y la necesidad de entender cómo han sido las prácticas para su combate.

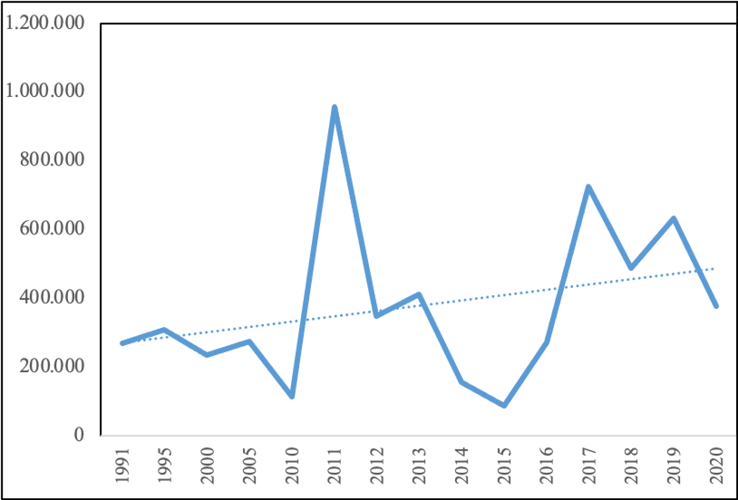
Fuente: Elaborado con datos de Comisión Nacional Forestal, Gerencia del Manejo del Fuego, marzo, 2021.

Figura 1. Comportamiento de la Superficie Forestal Afectada por Incendios (SFAI) en México, 1991-2020.

Figure 1. Tendency of the Average Forest Area Affected by Fires (FAAF) in Mexico, 1991-2020

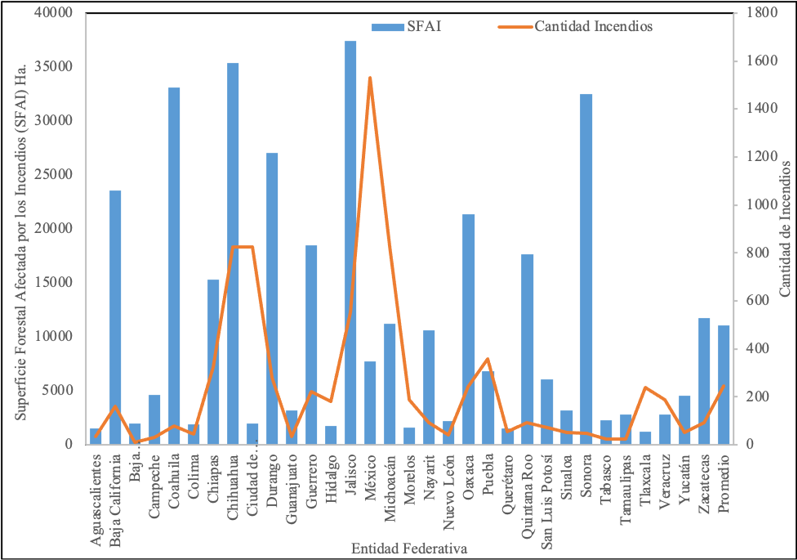
Fuente: Elaborado con datos de Comisión Nacional Forestal, Gerencia del Manejo del Fuego, marzo, 2021.

Figura 2. Promedio de SFAI y de NIF por Entidad Federativa, 1991-2020.

Figure 2. Average Forest Area Affected by Fires (FAAF) and Quantity of Forest Fires (QFF) by Federative State, 1991-2020

3. Marco teórico

Para prevenir y combatir los incendios forestales, es importante conocer los factores naturales y antropogénicos asociados con el siniestro. Esta tarea se puede hacer mediante: índices (vulnerabilidad, peligro, riesgo, etc.) y modelos estadísticos. Ambos instrumentos se emplean para detectar y combatir incendios forestales. Algunos factores causantes tienen que ver con condiciones aleatorias (estado del tiempo, combustible, dirección del viento y hora del evento), otros inciden directamente en la atención a la superficie afectada como la detección, llegada y combate de incendios forestales que dependen de la actuación humana y el despacho de los recursos económicos y materiales para realizar las acciones establecidas en un tiempo determinado (Rodríguez Trejo et al., 2008).

De esta manera, la SFAI está determinada por una conjugación de factores, físicos, meteorológicos y socioeconómicos. Los socioeconómicos que inciden de manera significativa en dicha explicación son: descuidos, accidentes, negligencia, intencionalidad, agricultura, tala ilegal y pastoreo (Cosgun & González-Cabán, 2019). Una explicación modelada se puede realizar a través de la generación de ecuaciones que describen dicha asociación (Rodríguez Trejo et al., 2008) o estiman los costos de la planificación mediante instrumentos econométricos (Rodríguez y Silva, 2019).

En contextos con incendios forestales, predecir la presencia, modelar el comportamiento y estimar los daños de los siniestros no es suficiente. Los estudios realizados en el tema en México señalan que la SFAI, la velocidad del viento y el número de productores agrícolas apoyados durante el ciclo productivo primavera-verano tuvieron una correlación positiva con variables dependientes relacionadas con el siniestro como el número de incendios y la superficie afectada. También se encontró correlación negativa entre alfabetización, esperanza de vida y número de combatientes; denotando que a mayor valor en estas variables se tienen menos SFAI y NIF (Rodríguez Trejo et al., 2008).

En otro estudio se identificó que las variables superficie del bosque, producto interno bruto per cápita y la longitud de carreteras, se encuentran relacionadas positivamente con la probabilidad de NIF y negativamente con la SFAI (Cruz-Espíndola et al., 2017). Se presentan también estudios que plantean un modelo conceptual del potencial de los incendios forestales para el Estado de Durango, México, mediante Sistemas de Información Geográfica, empleando variables físicas, ecológicas y antropogénicas asociadas con patrones de recurrencia de áreas incendiadas. Este modelo puede brindar apoyo a los administradores del bosque, para definir donde podrían ocurrir los incendios forestales y, con ello, alistar los planes de prevención y supresión (Pompa García et al., 2012).

También para Durango, se aplicó un análisis espaciotemporal de el NIF para determinar los factores más importantes que inciden en el tamaño de los incendios. Mediante una regresión geográficamente ponderada en función de la distancia, se encontró que el tamaño de los incendios se manifiesta de acuerdo con la densidad de la población y vías de acceso. A la vez que las bajas precipitaciones y altas temperaturas son factores climáticos que favorecen el NIF (Pérez-Verdín et al., 2013).

Si bien algunos estudios señalan que el número de combatientes de incendios y la longitud de carreteras tienen una relación negativa en la superficie siniestrada (Cruz-Espíndola et al., 2017; Rodríguez Trejo et al., 2008), también hay evidencia que el tamaño del incendio se expande en función de las vías de acceso y la distancia de estas (Pérez-Verdín et al., 2013). Se encuentran también los modelos sobre potencial y probabilidad de ocurrencia de incendios forestales (Cruz-Espíndola et al., 2017; Pompa García et al., 2012), así como los modelos sobre causalidad y eficiencia en el combate a incendios forestales (Ynouye-Francés et al., 2021) e índices de eficiencia para la protección contra incendios (Rodríguez y Silva, & González-Cabán, 2016; Rodríguez, et al., 2008). También es conocido que las variables biofísicas como humedad relativa, temperatura o cantidad de biomasa combustible disponible influyen (Cruz-Espíndola et al., 2017; Pompa García et al., 2012; Rodríguez et al., 2008).

Las variables propuestas en este trabajo (detección -De-, Tiempo de llegada TLI, temperatura -T-, detección -De- y duración -Dur- de incendios forestales sobre la SFAI) no han sido consideradas en la construcción de modelos estadísticos en México, que validen dicha relación. Para estudiar los factores que inciden en la SFAI, estos son elementos importantes. Sin embargo, la delimitación de la zona de estudio puede o no tomar en cuenta estos aspectos, así como el relieve y la vulnerabilidad (Vargas-Sanabria & Quesada-Román, 2018) en la previsión de la SFAI. De manera que, en una escala de análisis con una delimitación geográfica precisa, (cuenca, localidad, área natural -protegida o no-, núcleo rural, etc.) hay factibilidad de emplear dichas variables, dado que se trata de una superficie acotada.

El caso de estudio se integra de 11 entidades federativas, conocido como Región Centro-Occidente de México y tienen diferentes tipos de ecosistemas forestales, condiciones biofísicas, sociopolíticas, económicas y administrativas; tanto en las causas como en la atención a los incendios forestales. Por ello, el presente experimento retoma variables comunes, esperando encontrar efectos comunes a la explicación de la SFAI. No obstante, se ha tomado, como experimental, la variable temperatura lo que permitió corroborar que no es viable emplear esta variable a dicha escala.

El objetivo de la investigación fue plantear un modelo estadístico que ayude a identificar los determinantes de la SFAI, en la Región Occidente de México. En este sentido, se propone aportar información inicial para el fortalecimiento de un esquema para prevención de incendios. Las variables empleadas fueron: duración del incendio (Dur), número de incendios (NIF), detección de incendios (De), temperatura (T) y tiempo de llegada al incendio (TLI).

4. Metodología

4.1. Conceptualización de las variables

Las variables que pueden incidir en la eficiencia para el combate de los incendios forestales y su relación con la SFAI se seleccionaron de acuerdo con los estudios consultados (Castillo Sarasty, 2021; Cruz-Espíndola et al., 2017; Pérez-Verdín et al., 2013; Pompa García et al., 2012; Rodríguez Trejo, 2002; Rodríguez et al., 2008; Rodríguez y Silva, 2019; Ynouye-Francés et al., 2021), que sugieren estas variables (entre otras) afectan la eficiencia para el manejo de incendios. En un primer término, SFAI estaría siendo afectada por el número de incendios forestales (NIF), una variable del tiempo atmosférico, temperatura (T) y, en un segundo momento, influirían las variables de la eficiencia en el combate de incendios: detección de incendios (De), tiempo de llegada (TLI) y la duración del incendio (Dur), las cuales se presentan en el (Cuadro 1) y son las siguientes:

a)SFAI: es la cantidad de superficie afectada por incendios forestales durante un año (ha/año).

b)NIF: cantidad de incendios forestales presentados por Entidad Federativa por año.

c)Temperatura (T): es la cantidad de calor que un cuerpo o el aire tiene. Se expresa en grados centígrados.

i)Existe una relación inversa entre la temperatura y la humedad del aire; por ello, el binomio temperatura-humedad relativa influye en el peligro de incendio forestal, marca los parámetros de seguridad dentro de los que se deben conducir quemas prescritas, así como la apertura de líneas negras (Rodríguez Trejo, 2015).

b)Detección de incendios (De): es la acción de percatarse de la existencia de un incendio (expresada en segundos y minutos).

i)La detección oportuna permite que una vez reportado a las brigadas contra incendios, sea combatido, controlado y liquidado tan pronto como sea posible y con mayor seguridad, ya que el fuego apenas inicia y las llamas pueden ser controladas más rápidamente; reduciéndose la superficie afectada y los daños a la vegetación. Esta actividad se realiza por medios terrestres, aéreos y vía satélite (Rodríguez Trejo, 2002; Rodríguez Trejo et al., 2002).

b)Llegada al incendio: es el traslado de una brigada, generalmente la más cercana al incendio (expresada en segundos y minutos); es decir cuando un incendio es detectado, ya sea por medios fijos o móviles, se informa al despacho y la brigada más cercana al siniestro será la encargada de realizar el primer ataque.

i)Dicha brigada debe informar la ubicación y superficie que cubre el incendio, la hora de salida al siniestro, la llegada al inicio de combate y el avance de las labores cuando se les solicite. Esta actividad se relaciona directamente con el despacho, el cual de acuerdo con Rodríguez Trejo et al. (2002) es la distribución óptima y ágil de los recursos humanos y materiales como: brigadas terrestres, aeronaves, tractores oruga, herramientas, equipo entre otros, disponibles para una eficaz prevención, combate y control de los incendios forestales.

b)Combate de incendios forestales (duración): son todas las acciones que tiene como objetivo controlar el incendio (expresado en minutos y horas).

i)Puede ser directo o indirecto. El primero liquida al fuego con bate-fuegos, aplicando tierra con palas a la base de las llamas, agua con mochilas aspersoras, motobombas, camiones motobomba, mediante avión cisterna o helibalde. Se considera ataque directo a la apertura de brechas cortafuego y la aplicación de agua con retardante cerca de las llamas. El combate indirecto consiste en la apertura de brechas cortafuego lejos del incendio. Uno de los elementos básicos que integran el combate de incendios forestales es la estrategia que es el plan general de acción para combatir el incendio, de modo que se haga el uso más eficiente posible de personal y equipo (Rodríguez Trejo, 2015).

Cuadro 1. Variables e indicadores.

Table 1. Variables e indicadores.

Variable dependiente	Variables independientes	Indicadores
SFAI	NIF (Ocurrencia de Incendios)	Cantidad de incendios en un año
	T	Temperatura promedio anual en °C.
	De	Tiempo en minutos
	TLI	Tiempo en minutos
	Dur	Tiempo expresado en minutos

El modelo estadístico se desarrolló con datos panel organizados anualmente de 1995 a 2016, para 11 entidades federativas de la Región Centro Occidente de México. Estas fueron: Colima, Ciudad de México, Guanajuato, Hidalgo, Jalisco, Estado de México, Michoacán, Morelos, Puebla, Querétaro y Tlaxcala. Los criterios para la selección de estos estados fueron tres: es la región con mayor cantidad de incendios en México (promedio anual y período de estudio); se trata de una muestra que da cuenta de la situación general en el país; y se pudo disponer de la información necesaria.

La información fue recabada en estadísticas anuales del Programa Nacional de Prevención de Incendios Forestales de la Comisión Nacional Forestal (CONAFOR, 2017; CONAFOR, 2021) y las variables meteorológicas se obtuvieron del servicio meteorológico nacional (SMN, 2017).

Se usaron las aplicaciones, XLSTAT y Eviews, para analizar los datos y realizar las siguientes pruebas: componentes principales, prueba de redundancia, prueba de raíz unitaria, prueba de Hausman, modelos de regresión de datos panel y prueba de redundancia de efectos fijos en logaritmos, normalidad de los residuales, autocorrelación, heterocedasticidad y multicolinealidad.

La primera prueba tuvo como propósito realizar una exploración del comportamiento de las variables, sus interrelaciones y explicar en términos de sus relaciones subyacentes comunes (factores) (Hair et al., 2007). Las demás pruebas fueron para corroborar o contrastar lo encontrado en el análisis de componentes principales y para conocer los determinantes de la SFAI, mediante un modelo que permita identificar el impacto por variable y su significancia estadística. El modelo se puede representar según se indica en la Ecuación 1, siguiendo los criterios de especificación de Gujarati y Porter (2010, p. 468).

Yit = ait + β1X1it + β2X2it +… + βkXkit + Uit; con i= 1, 2, 3… n y t=1, 2, 3…. t. (E. 1)

Donde:

i = unidad de estudio

t = tiempo

Yit = Variable dependiente

Xit = Variables independientes, es la i-ésima observación en el momento t, para las k variables explicativas (X1, X2,…,Xk).

ait = Interceptos que puede contener (1 o n+t) parámetros

β1, β2,…..,βK = Parámetros

Uit = Error compuesto (no observables, no cuantificables y error aleatorio).

Las pruebas estadísticas de normalidad, raíz unitaria, Hausman y redundancia se emplearon para detectar errores de especificación ecuacional, verificar el comportamiento de las variables, conocer el tipo de relación y su significancia estadística para validar si son o no relaciones espurias (Gujarati & Porter, 2010).

4.2. Análisis de Componentes Principales (ACP)

En el (Cuadro 2) se aprecia que las variables De, TLI y Dur tienen una misma dirección, además, se comportan de forma paralela, lo que se aprecia en los vectores propios y sugeriría que las variables se podrían agrupar según el comportamiento semejante de su varianza …dado que las comunalidades son estimaciones de la varianza compartida o común entre las variables, los factores (F) que resultan del análisis factorial común se basan solamente en la varianza común (Hair et al., 2007, p. 91).

Las cargas factoriales más altas en el Factor F1 se obtuvieron para De, TLl y Dur con signo positivo y contribución de 23 %, 24 % y 24 % respectivamente. Por tal motivo, este factor se identifica con la eficacia en el combate, dado que son variables en cierto control. El factor F2 se identifica con las variables SFAI y NIF, cargas factoriales altas y 90 % de contribución a la variable. Ambas variables se identifican con el evento, incendios y su afectación. F1 y F2 aportan 64 % del comportamiento de la varianza. La variable T destaca en el F3 con un comportamiento distinto y contribuye 16 % a la varianza total (Cuadro 2).

Cuadro 2. Análisis de Componentes Principales (ACP).

Table 2. Principal Component Analysis (PCA).

Vectores propios:
	F1		F2		F3		F4		F5
SFAI	-0.028		0.749		0.357		-0.114		-0.509
NIF	-0.348		0.584		-0.188		0.332		0.574
T	0.394		-0.079		0.661		0.546		0.083
De	0.480		0.131		-0.434		0.514		-0.042
TLI	0.494		0.203		-0.417		-0.169		-0.242
Dur	0.498		0.183		0.197		-0.534		0.587
Cargas factoriales:
	F1		F2		F3		F4		F5
SFAI	-0.044		0.869		0.351		-0.081		-0.320
NIF	-0.552		0.678		-0.185		0.234		0.361
T	0.626		-0.092		0.650		0.385		0.052
De	0.762		0.152		-0.427		0.362		-0.027
TLI	0.784		0.236		-0.410		-0.119		-0.152
Dur	0.791		0.213		0.194		-0.377		0.369
Correlaciones entre las variables y los factores:
	F1		F2		F3		F4		F5
SFAI	-0.044		0.869		0.351		-0.081		-0.320
NIF	-0.552		0.678		-0.185		0.234		0.361
T	0.626		-0.092		0.650		0.385		0.052
De	0.762		0.152		-0.427		0.362		-0.027
TLI	0.784		0.236		-0.410		-0.119		-0.152
Dur	0.791		0.213		0.194		-0.377		0.369
Contribuciones de las variables (%):
	F1		F2		F3		F4		F5
SFAI	0.076		56.074		12.740		1.310		25.941
NIF	12.084		34.095		3.530		11.017		32.939
T	15.552		0.622		43.640		29.853		0.692
De	23.059		1.718		18.836		26.398		0.179
TLI	24.385		4.132		17.371		2.866		5.844
Dur	24.844		3.359		3.883		28.556		34.406
Valores propios y aporte a la varianza por factor:
		F1		F2		F3		F4		F5	F6
Valor propio		2.518		1.347		0.968		0.497		0.395	0.275
Variabilidad (%)		41.969		22.445		16.130		8.286		6.588	4.583
Acumulado		41.969		64.413		80.544		88.829		95.417	100.000

Fuente: Elaborado con datos de CONAFOR (2021).

En suma, el ACP sugiere que De, TLI y Dur se agrupan en un factor en tanto que SFAI y NIF, en otro, de acuerdo con el comportamiento de su varianza; en tanto que “T” sigue una lógica distinta. Esto proporciona una visión del comportamiento en comunalidades de las variables y que las seis variables se pueden resumir a tres factores que estarían explicando la mayor parte del comportamiento de la varianza (Hair et al., 2007). Las implicaciones de esta información ayudarían a justificar las variables; debido a que: De, TLl y Dur refieren eficiencia en el combate a incendios, son variables de respuesta al evento y, al parecer, se repite información entre estas. Por esta razón, se supondría que el modelo estadístico puede arrojar información sobre la respuesta de cada variable, esto apoya para tener mayor eficacia en el combate a los incendios.

5. Resultados

La eficacia de las acciones públicas para el combate a los incendios forestales aborda dos elementos: la previsión y la mitigación/eliminación del daño. En el primer caso se trata del conjunto de acciones que pretenden evitar los incendios, en tanto que el segundo caso es el combate a estos. La SFAI es entonces la consecuencia del desarrollo de ambas acciones, el modelo que se propone retomar la perspectiva desde la evidencia, en tanto a las variables de respuesta, es decir, el combate a los incendios. Como se ha podido apreciar, el ACP apunta un comportamiento relacional entre las variables, ahora se revisará si las variables NIF, T, De, TLI y Dur, encierran información que ayude a explicar la SFAI; para ello, se plantea el análisis de panel de datos y las pruebas estadísticas.

5.1. Análisis de redundancia y pruebas de raíz unitaria

La prueba de redundancia con sección cruzada y efectos fijos de la variable dependiente SFAI y las variables independientes: NIF, T, TLI, De y Dur, sugiere que para las variables De y T no se puede rechazar la hipótesis nula de no redundancia ver (Cuadro 3), (véase Greene, 2012). Como se aprecia las variables T y De, no pasan la prueba de análisis de redundancia de sección cruzada, de manera que no son consistentes para la prueba de raíz unitaria, lo que lleva realizar una reducción de variables reduciendo, a su vez, la probabilidad de colinealidad (Gujarati & Porter, 2012).

Cuadro 3. Análisis de redundancia.

Table 3. Redundance análisis.

Variable	Coeficiente	Error Estándar	Estadística de t	Valor P
C	1.967800	1.345254	1.462773	0.1447
NIF	1.184123	0.044660	26.51425	0.0000
T	-0.396019	0.427121	-0.927181	0.3546
TLI	0.281055	0.082041	3.425780	0.0007
De	0.114268	0.072114	-1.584548	0.1142
Dur	0.732573	0.069424	10.69259	0.0000

Fuente: Elaborado con información de CONAFOR, 2017 y 2021.

Cuadro 4. Pruebas de raíz unitaria para las variables.

Table 4. Unit root test variables.

Variable	Pruebas	Significancia estadística	Nivel de integración
SFAI	1. Levin, Lin y Chu 2. Im, Pesaran and Shin W-stat. 3. ADF - Fisher Chi-square. 4. PP - Fisher Chi-square.	Con un (α= 0.01) y un nivel de confianza del 99 %.	Nivel de integración I(0)
NIF	1. Levin, Lin y Chu 2. Im, Pesaran and Shin W-stat. 3. ADF - Fisher Chi-square. 4. PP - Fisher Chi-square.	Con una (α= 0.05) y un nivel de confianza del 95 % (para la prueba Levin, Lin & Chu) y (α= 0.01) y un nivel de confianza del 99 %.	Nivel de integración I(0)
Dur	1. Levin, Lin y Chu 2. Im, Pesaran and Shin W-stat. 3. ADF - Fisher Chi-square. 4. PP - Fisher Chi-square.	Con una (α=0.01) y un nivel de confianza del 99 %.	Nivel de integración I(0)

Fuente: Elaborado con información de CONAFOR, 2017 y 2021.

Considerando el análisis general de las pruebas de raíz unitaria; la prueba de Im, Pesaran y Shin W-stat, fue la más consistente, tanto para la variable dependiente SFAI como las variables NIF y Dur para un nivel de significancia (α= 0.01) y un nivel de confianza del 99%, se rechaza la hipótesis nula; ya que dichas variables no tienen raíz unitaria, es decir, son variables estacionarias y tienen un grado de integración cero I (0) (Ver Cuadro 4) (véase Greene, 2012; Gujarati & Porter, 2012).

5.2. Prueba de Hausman

La prueba Hausman indica el tipo de modelo que se utilizará en el análisis de datos a fin reducir los problemas de endogeneidad. Los resultados que se muestran en el (Cuadro 5) indican que para un modelo de sección cruzada y período aleatorio una significancia estadística (α=0.01) y un nivel de confianza del 99 %; al menos un coeficiente es diferente de las variables: NIF, Dur y SFAI; por lo tanto, se utilizaron efectos fijos tanto para la sección cruzada y período en el modelo de regresión (Montero Granados, 2005).

Cuadro 5. Prueba de Hausman.

Table 5. Hausman test.

Prueba	Chi-cuadrada (estadístico)	Chi-cuadrada (d.f)	Prob.
Sección cruzada aleatoria	0.000000	2	1.0000
Periodo aleatorio	0.000000	2	1.0000
Sección cruzada y periodo aleatorio	50.200848	2	0.0000

Fuente: Elaborado con datos de CONAFOR, 2017 y 2021.

5.3. TLl, NIF y Dur como determinantes de la SFAI

Una vez realizadas las pruebas de raíz unitaria y Hausman se determinó el modelo de datos panel para las variables dependiente SFAI y explicativas NIF y Dur, siendo el siguiente:

Yit = ait + β1X1it + β2X2it +… + βkXkit + Uit; con i= 1, 2, 3,…n y t=1, 2, 3….t.

Donde:

i = unidad de estudio (Entidad federativa)

t= tiempo (años de 1995 a 2016)

Yit = Variable dependiente SFAI

Xit = Variables independientes (TLl, NIF y Dur), es la i-ésima observación en el momento t, para las k variables explicativas (X1, X2,…,Xk).

ait = Interceptos que puede contener (1 o n+t) parámetros

β1, β2,…..,βK = Parámetros

Uit = Error compuesto (no observables, no cuantificables y error aleatorio)

5.4. Modelo de datos panel:

Para el análisis de regresión, se hizo la transformación a logaritmos y el modelo fue de datos panel con efectos fijos en sección cruzada de once entidades federativas de México durante el período 1995-2016. Los resultados se pueden apreciar en el (Cuadro 6), obteniendo una relación elástica para NIF e inelástica para Dur, ambos en signos positivos, lo que indica una relación directa. En el caso de la variable TLl, no pasó la prueba, por lo que no fue una variable significativa, manteniendo solo dos variables en el modelo, véase (Apéndice 1). En el Apéndice 2, se incluyen las pruebas estadísticas de bondad de ajuste del modelo.

Cuadro 6. Modelo estadístico .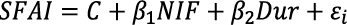

Table 6. Statistical model 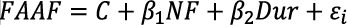*3.

	Coeficiente		Desv. Típica			Estadístico t	valor p
const	0.219579		0.291930			0.7522	0.4693
LogNIF	1.28413		0.0918763			13.98	<0.0001		***
LogDur	0.523415		0.135942			3.850	0.0032		***
Contraste de normalidad de los residuos Hipótesis nula: [El error tiene distribución Normal] Estadístico de contraste: Chi-cuadrado (2) = 4.16659 Con valor p = 0.124519
Media de la vble. dep.		3.277097			D.T. de la vble. dep.			0.615625
Suma de cuad. residuos		8.042817			D.T. de la regresión			0.196640
R-cuadrado MCVF (LSDV)		0.911944			R-cuadrado ‘intra’			0.898448
Log-verosimilitud		68.52004			Criterio de Akaike			−69.04008
Criterio de Schwarz		49.58381			Crit. de Hannan-Quinn			−21.25411
rho		−0.067306			Durbin-Watson			2.040714

Fuente: Elaborado con datos de CONAFOR (2017, 2021).

Con significancia α = 0.01 y un nivel de confianza del 99 %, ambas variables fueron significativas; por lo tanto, los coeficientes son consistentes e insesgados. En este sentido, las variables se relacionan positivamente en un grado de respuesta más que proporcional, ante un aumento en 1 % en NIF, la superficie incendiada responde en 1.28 %. Por el contrario, con Dur, la cual implica que ante un aumento del 1% en el tiempo de duración del incendio, la superficie incendiada aumentará 0.52 %. La R2 sugiere que el comportamiento en la variable dependiente es altamente explicado por las variables explicativas.

5.5. Pruebas de redundancia de efectos fijos para el modelo:

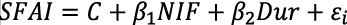
La prueba de redundancia del modelo estadístico: log (SFAI) = log (NIF) log (Dur), con significancia estadística (α=0.05) y nivel de confianza del 95 %, al menos un coeficiente no es redundante, como se muestran en el (Cuadro 7).

Cuadro 7. Prueba de redundancia de efectos fijos (logaritmos).

Table 7. Fixed effects redundancy test (logarithms).

Prueba de los efectos (F) y Ji-cuadrada (χ2)	Estadístico	D.f	Probabilidad
Sección cruzada F	21.105615	(10,208)	0.0000
Sección cruzada χ2	169.512976	10	0.0000
Período F	1.749073	(21,208)	0.0259
Período χ2	39.353962	21	0.0089
Sección cruzada/Período F	8.290954	(31,208)	0.0000
Sección cruzada/Período χ2	194.699027	31	0.0000

Fuente: Elaborado con datos de CONAFOR (2017, 2021).

Una vez realizadas las pruebas: regresión, redundancia y normalidad del modelo de datos panel log (SFAI)= log (NIF) + log (Dur); el modelo estadístico para explicar la SFAI por incendios para la Región Centro Occidente de México con los siguientes atributos: Log (SFAI) = 0.22 + 1.28*Log(NIF) + 0.52*Log(Dur). El modelo estaría explicando aproximadamente 90 % de los casos. Más allá de que se trate de un modelo que pretenda predecir el comportamiento, su contribución en la práctica es que Dur es una variable sobre la que se puede incidir e, incluso, tener un cierto grado de control desde la política contra incendios forestales, como variable de respuesta. En tanto que NIF sería una variable en la que se podría incidir solamente con previsión, por lo que ambas serían complementarias para las acciones de política forestal.

6. Discusión

El análisis de regresión evidenció que las variables NIF y Dur del incendio guardan una relación positiva con la superficie forestal afectada por incendio, lo cual concuerda con los hallazgos de Rodríguez Trejo et al. (2008) y Cruz-Espíndola et al. (2017), siendo el número de incendios el que más incide en el modelo, con un grado de respuesta más que proporcional; es decir, ante un aumento en 1 % en el número de incendios, la superficie incendiada responde en 1.28 %. Por el contrario, hay una respuesta inelástica entre duración y superficie ante un aumento del 1 % en el tiempo de duración del incendio, la superficie incendiada aumentará 0.52 %.

Este hallazgo concuerda con la predominancia de los modelos de simulación que se enfocan en su predicción de acuerdo al número de incendios e índices de peligro (Cruz-Espíndola et al., 2017; Pérez-Verdín et al., 2013; Pompa García et al., 2012; Rodríguez et al., 2008) que tienen como finalidad reducir la superficie forestal afectada por incendio; por consiguiente, tanto los modelos de eficiencia del combate de incendios forestales como la duración del siniestro pueden mejorar las decisiones y acciones gubernamentales en el combate y liquidación de los incendios.

El fuego ha constituido parte importante para la regeneración de algunos bosques (Kauffman, 1991; Pausas, 2020). En un trabajo experimental se aprecia que el fuego favoreció el establecimiento de la regeneración natural de P. montezumae en el área estudiada. Se demostró que la capa de hojarasca es un factor limitante en el establecimiento de la regeneración, evitando que la semilla se establezca al no encontrar condiciones adecuadas o, en su caso, que la raíz llegue a suelo mineral, sufriendo así un estrés hídrico y consecuentemente la muerte. Sin embargo, ya establecidas las plántulas, la hojarasca las protege de las heladas (Díaz-Hernández et al., 2021). Ante esto, se hace necesario mantener un control sobre el histórico de incendios y manejo preventivo de zonas. Para la Región Centro Occidente de México, se aprecia que las SFAI puede ser prevenida cuando se conocen las condiciones de las variables T, Dur, De y TLI.

En cuanto a las variables como detección y llegada al incendio, no se encuentran relacionadas con la superficie forestal afectada por incendios y el número de incendios; por lo tanto, las actividades de vigilancia del torrero (detección) y el traslado de la brigada al siniestro (llegada) no determina su afectación y ocurrencia. Lo anterior se puede deber a la distribución estratégica de las brigadas durante la temporada de incendios y la experiencia acumulada del personal operativo y administrativo del área de incendios; que han logrado tener una mayor eficiencia y eficacia en estas dos variables; no así en cuanto a la duración y ocurrencia de los incendios, que aunada a la falta de una cultura de prevención de incendios en México, de acuerdo a Rodríguez Trejo et al. (2002), reduce la eficiencia y eficacia de las acciones gubernamentales en la asignación de recursos humanos y materiales para el combate de incendios, ocasionando eventos catastróficos como los ocurridos en 1998, 2011 y 2013.

Esta hipótesis resalta la importancia que tienen las acciones de protección de la vegetación por parte de las instituciones oficiales y propietarios de los bosques, las cuales deben enfocarse directamente en la prevención de incendios como: apertura de brechas cortafuego, líneas negras y quemas prescritas; ya que existe una correlación positiva entre la cantidad de incendios y la superficie forestal afectada (CONAFOR, 2010). Además, con la implementación de actividades preventivas, se pueden obtener otros beneficios en la asignación de recursos durante la temporada de incendios forestales como: facilitar las actividades de llegada y combate del incendio forestal, con lo cual se reduciría la intensidad y afectación a la vegetación existente; así como el tiempo de combate del incendio (Pausas, 2020; Rodríguez Trejo, 2015). Es decir, hace más eficaz y eficiente la asignación de recursos humanos, equipo y materiales destinados al combate de incendios forestales, dado que se reduce los tiempos empleados en cada una de las actividades: detección, llegada y combate; evitando su propagación y disminuyendo su peligro.

El trabajo de Muñoz-Robles et al., (2005) encuentra que conocer la distribución del peligro de incendios dentro del ejido Corona del Rosal permite generar estrategias de control y combate de incendios forestales, de tal manera que los recursos humanos destinados para las labores de control y combate serán dirigidos a las zonas donde se espera un mayor grado de peligro. Para esto, el análisis multicriterio constituye una herramienta fundamental para las estrategias de combate a los incendios (Muñoz-Robles et al., 2005). En este sentido, el modelo planteado se puede extender a otras entidades y aportar información para dicho análisis al momento del diseño de estrategias de combate, como un aporte modesto en el marco de la información suficiente para la toma de decisión.

Respecto al modelo estadístico, este considera la eficiencia en el combate en los incendios; por lo tanto, amplía el conocimiento respecto al modelaje de los incendios forestales en México; ya que complementa los modelos existentes de prevención, detección y combate de incendios forestales; con lo cual, de acuerdo con Vega García et al. (1999), se puede realizar una mejor distribución de recursos de extinción más eficiente y puede reducir costos, perdidas y daños. Además, se puede complementar con los modelos de simulación que predicen la ocurrencia de incendios en sitios específicos como los desarrollados por Pompa García et al. (2012); a fin de planear los programas y acciones gubernamentales para la supresión de los incendios forestales, a fin de reducir su magnitud.

En el trabajo de Pérez-Verdín et al. (2013), se presenta un modelo de regresión espacial y recomiendan el uso de técnicas estadísticas, variables estocásticas, como las que se usan en el presente trabajo, lo que apoya a seguir explorando el uso de este tipo de instrumentos provenientes de la econometría. Lo anterior dado uno de los hallazgos de dicho trabajo: la no estacionalidad sugiere que el tamaño de los incendios forestales depende de su posición geográfica y de la influencia de los factores antes mencionados (Pérez-Verdín et al., 2013), lo cual se afirma también para el presente trabajo, aunque con otras variables y otra escala de trabajo. No obstante, se presenta una línea de investigación prometedora.

El presente modelo constituye una propuesta inicial para el análisis a una escala “macro” de la SFAI. Se pueden agregar variables para robustecer el alcance y, con ello, llegar a mayor precisión en la prevención de incendios. No obstante, es importante destacar la importancia de contar con más variables disponibles en información homogénea. Por otra parte, a una escala de cuenca (por ejemplo), se puede proponer un modelo semejante incorporando las variables que sugieren los estudios de Pérez-Verdín et al. (2013); Vargas-Sanabria y Quesada-Román (2018) y Muñoz-Robles et al. (2005), lo que abre una línea de investigación de la aplicación de los métodos estadísticos provenientes de la econometría a sus aplicaciones en el campo de la prevención de incendios forestales.

7. Conclusiones

El uso de modelos estadísticos o de simulación es una herramienta útil que puede ayudar a planificar acciones de protección forestal y a elegir las mejores estrategias de prevención, detección, despacho, combate y liquidación de incendios. Sin embargo, los existentes son utilizados para identificar y combatir incendios forestales. Por esto, el modelo obtenido abarca otros derroteros y puede utilizarse en la distribución eficiente y eficaz de los recursos humanos, materiales y equipo; a fin de que los siniestros tengan una menor duración e intensidad. Es decir, asignar los mayores recursos en los lugares donde existe la mayor probabilidad de ocurrencia de incendios, con la finalidad de reducir la superficie forestal afectada por incendios, pero sobre todo su magnitud. Si bien, se puede intuir cómo interactúan las variables que se presentan en este trabajo (SFAI, Dur, T, TLI y De), el aporte consiste en darles forma relacional y una medición que sea justificada, para lo cual ha sido de gran ayuda el análisis de componentes principales.

Los resultados apuntan a que, en la Región Centro Occidente de México, (11 entidades federativas) existe una relación entre NIF y Dur, más que proporcional para NIF (1.28) y menos que proporcional para la Dur (0.52), en relación con la SFAI. Las otras variables: De, TLl y T; para las dos primeras se trata variables de gestión, que se deben atender desde la perspectiva del manejo preventivo. La temperatura es una variable exógena que es importante para el monitoreo en la temporada de incendios, como se pudo apreciar en los resultados de otras investigaciones y su tratamiento estadístico, más bien, va acompañado de otras variables que inciden en los incendios, desde el aspecto bio-físico.

Debido a que SFAI y su intensidad tienen una correlación positiva con el NIF y su duración; los programas de incendios forestales deben contar la estadística histórica, el pronóstico de las condiciones climáticas, las cargas de combustibles y las características topográficas del lugar; pero principalmente los recursos humanos, equipo y materiales disponibles para implementar acciones eficientes y eficaces contra incendios forestales; además, dicha información permite realizar adecuaciones presupuestales ante la presencia de la Oscilación del Sur o fenómeno conocido como el niño a fin de evitar incendios catastróficos como los presentados en 1998, 2011, 2013 y 2017, que causaron pérdidas humanas, económicas y de servicios ecosistémicos.

La política de protección de la vegetación forestal por parte de las instituciones oficiales debe enfocarse en el manejo del fuego, a través de quemas prescritas, apertura de brechas cortafuego y líneas negras; ya que estas actividades reducen el número e intensidad de los incendios que se presentan en una zona o región específica; así como despachar de manera eficiente los recursos humanos y materiales destinados para esta actividad.

8. Agradecimientos

Al Dr. Plinio Hernández-Barriga, Al instituto de Investigaciones Económicas y Empresariales, a la Universidad Michoacana. A la Universidad Michoacana de San Nicolás de Hidalgo, a la Revista de Ciencias Ambientales y a las personas revisoras anónimas por sus aportes a la versión final del escrito.

9. Ética y conflicto de intereses

Las personas autoras declaran que han cumplido totalmente todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en la producción del manuscrito; que no hay conflicto de interés de ningún tipo; que todas las fuentes financieras se mencionan completa y claramente en la sección de agradecimientos, y que están totalmente de acuerdo con la versión final editada del artículo.

10. Referencias

Armenteras, D., Dávalos, L. M., Barreto, J. S., Miranda, A., Hernández-Moreno, A., Zamorano-Elgueta, C., Gónzalez-Delgado, T. M., Meza-Elizalde, M. C., & Retana, J. (2021). Fire-induced loss of the world’s most biodiverse forests in Latin America. Science Advances, 7(33). 1-8. https://doi.org:10.1126/sciadv.abd3357

Balvanera, P. (2012). Los servicios ecosistémicos que ofrecen los bosques tropicales. Ecosistemas, 21 (1-2), 136-144. https://doi.org/10.7818/ECOS.33

Castillo Sarasty, J. E. (2021). Prototipo web para predicción y detección de incendios forestales en los cerros orientales de Bogotá, mediante una red de sensores e inteligencia artificial. [Tesis de grado, Universidad Piloto de Colombia]. Repositorio Institucional Universidad Piloto de Colombia. http://repository.unipiloto.edu.co/bitstream/handle/20.500.12277/9883/PROTOTIPO%20WEB%20PARA%20PREDICCION%20Y%20%20DETECCI%c3%93N%20Sistemas.pdf?sequence=1&isAllowed=y

Cerano-Paredes, J., Villanueva-Díaz, J., Vázquez-Selem, L., Cervantes-Martínez, R., Esquivel-Arriaga, G., Guerra-de la Cruz, V., & Fulé, P. (2016). Régimen histórico de incendios y su relación con el clima en un bosque de Pinus hartwegii al norte del estado de Puebla, México. Bosque (Valdivia), 37(2), 389-399. ∑https://dx.doi.org/10.4067/S0717-92002016000200017

Comisión Nacional Forestal, Gerencia del Manejo del Fuego (2021, marzo). Número de incendios [Base de datos]. Gobierno de México http://dgeiawf.semarnat.gob.mx:8080/ibi_apps/WFServlet?IBIF_ex=D3_RFORESTA05_01&IBIC_user=dgeia_mce&IBIC_pass=dgeia_mce&NOMBREENTIDAD=*&NOMBREANIO=*

CONAFOR (2010). Incendios forestales. Guía práctica para comunicadores (3ra ed.). CONAFOR. http://www.conafor.gob.mx:8080/documentos/docs/10/236Gu%C3%ADa%20pr%C3%A1ctica%20para%20comunicadores%20-%20Incendios%20Forestales.pdf

CONAFOR (2017). Programa nacional de prevención de incendios forestales. Reporte de estadísticas 1995-2016. http://www.conafor.gob.mx/web/temas-forestales/incendios/

Cosgun, U. & González-Cabán, A. (2019). Factores Socioeconómicos que Afectan a los Incendios Forestales: Un Estudio de Caso de Antalya, Turquía. En Armando González-Cabán y José J. Sánchez (Coord.), Quinto Simposio Internacional Sobre Políticas, Planificación, y Economía de los Incendios Forestales: Servicios Ambientales e Incendios Forestales. [Memoria de Simposio]. Pp. 107-108. Servicio Forestal del Departamento de Agricultura. Estados Unidos. https://doi.org/10.2737/PSW-GTR-261-ES

Cruz-Espíndola, M. Á., Rodríguez-Trejo, D. A., Villanueva-Morales, A., & Santillán-Pérez, J. (2017). Factores sociales de uso del suelo y vegetación asociados a los incendios forestales en Hidalgo. Revista Mexicana de Ciencias Forestales, 8(41). https://doi.org/10.29298/rmcf.v8i41.29

Díaz-Hernández, D., Rodríguez-Laguna, R., Rodríguez-Trejo, D. A., Acevedo-Sandoval, A., & Maycotte-Morales, C. C. (2021). Dinámica de la regeneración de Pinus montezumae posterior a un incendio y a quema prescrita. Botanical Sciences, 99(1), 58-66. https://doi.org/10.17129/botsci.2634

FAO (2020). Yearbook of Forest Products 2018. Ed. FAO. https://doi.org/10.4060/cb0513m.

Flores-Garnica, J., Reyes-Alvarado, A., & Reyes-Cárdenas, O. (2021). Relación espaciotemporal de puntos de calor con superficies agropecuarias y forestales en San Luis Potosí, México. Revista Mexicana de Ciencias Forestales, 12(64) 127-145. https://doi.org/10.29298/rmcf.v12i64.857

González-Ramírez, L. M., Galicia, L., & González-Mendoza, L. (2007). El efecto de El Niño ENSO en la presencia de incendios forestales extremos. En Global Fire Monitoring Center, [Conferencia Internacional sobre Incendios Forestales] (pp. 13-18). https://www.researchgate.net/profile/Leopoldo-Galicia/publication/268513749_El_efecto_de_El_Nino_ENSO_en_la_presencia_de_incendios_forestales_extremos/links/546e17d20cf29806ec2e7b7b/El-efecto-de-El-Nino-ENSO-en-la-presencia-de-incendios-forestales-extremos.pdf

Greene, W. H. (2012). Econometric analysis (17va ed.). Pearson.

Guitián Rivera, L. (1999). Los incendios forestales a través de la Historia: pervivencias y cambios en el uso del fuego en el noroeste peninsular. En F. Araque Jiménez (Coord.), Incendios Históricos. Una aproximación multidisciplinar (pp. 149-162). Universidad Internacional de Andalucía. Baeza. https://dspace.unia.es/bitstream/handle/10334/2313/149-162Guitian.pdf?sequence=26&isAllowed=y

Gujarati, D., & Porter, D. (2010). Econometría (5ta ed.). Mc. Graw Hill.

Hair, J. F., Anderson, R. E., Tatham, R. L., & Black, W. C. (2007). Análisis Multivariante. Pearson

Harnecker, B., Vásquez, J., & Ortega, R. (2020). Las publicaciones científicas sobre incendios forestales están creciendo y tienen una gran presencia regional. https://conectaresiliencia.cl/investigacion-incendios/

Kauffman, J. B. (1991). Survival by sprouting following fire in tropical forests of the eastern Amazon. Biotropica, 23, 219–224. https://doi.org/10.2307/2388198

Loomis, J., Sánchez, J. J., González-Cabán, D.R., Rideout, D., & Reich, R. (2019). ¿Los tratamientos de combustible reducen los costos de supresión de incendios forestales y daños a la propiedad? Análisis de los costos de supresión y daños a la propiedad en los bosques nacionales de los Estados Unidos”. En Armando González-Cabán y José J. Sánchez (Coord.), Quinto Simposio Internacional Sobre Políticas, Planificación, y Economía de los Incendios Forestales: Servicios Ambientales e Incendios Forestales. [Memoria de Simposio]. Pp. 78-94. Servicio Forestal del Departamento de Agricultura. Estados Unidos. https://doi.org/10.2737/PSW-GTR-261-ES

Macías Macías, A., & Sevilla García, Y. L. (2021). Naturaleza vulnerada. Cuatro décadas de agricultura industrializada de frutas y hortalizas en el sur de Jalisco, México (1980–2020). EntreDiversidades: Revista de Ciencias Sociales y Humanidades, 8(1), 64-91. https://doi.org/10.31644/ED.V8.N1.2021.A03

Magaña Rueda, V., Pérez, J. L., & Conde, C. (1998). El niño y la oscilación del sur, sus impactos en México. Ciencias, 51, 14-18. https://www.revistacienciasunam.com/es/108-revistas/revista-ciencias-51/907-el-fenomeno-del-el-nino-y-la-oscilacion-del-sur-sus-impactos-en-mexico.html

Manzo-Delgado, L. L., & López-García, J. (2020). Análisis espacial y temporal de áreas quemadas en 1998, 2003 y 2015 en la Reserva de la Biosfera Montes Azules, Chiapas, México. Bosque, 41(1), 11-24. https://doi.org/10.4067/S0717-92002020000100011

Montero Granados, R. (2005). Test de Hausman. [Documentos de Trabajo en Economía Aplicada. Universidad de Granada. España]. https://www.ugr.es/~montero/matematicas/hausman.pdf

Muñoz-Robles, C. A., Treviño Garza, E. J., Verástegui Chávez, J., Jiménez Pérez, J., & Calderón Aguirre, O. A. (2005). Desarrollo de un modelo espacial para la evaluación del peligro de incendios forestales en la Sierra Madre Oriental de México. Investigaciones geográficas, 56, 101-117. https://doi.org/10.14350/rig.30099

Ocampo Zuleta, K. (2016). Valoración económica de incendios forestales en las principales ciudades de América Latina y el Caribe: una lección para Bogotá. Revista de Investigaciones de Uniagraria, 4(1), 75-89. https://www.uniagraria.edu.co/wp-content/uploads/2021/06/Revista_Vol.4_DIGITAL.pdf

Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). (2020). Evaluación de los recursos forestales mundiales 2020. http://www.fao.org/3/ca9825es/ca9825es.pdf

Parra Lara, Á. D. C. (Ed.) (2011). Incendios de la cobertura vegetal en Colombia. Ed. Universidad Autónoma de Occidente, RCFA y PNUMA.

Pausas, J. G. (2020). Incendios forestales, una visión desde la ecología. Consejo Superior de Investigaciones Científicas (España) y Libros de la Catarata. https://digital.csic.es/handle/10261/56575

Pérez-Verdín, G., Márquez-Linares, M. A., Cortes-Ortiz, A., & Salmerón-Macías, M. (2013). Análisis espacio-temporal de la ocurrencia de incendios forestales en Durango, México. Madera y Bosques, 19 (2), 37-58. https://doi.org/10.21829/myb.2013.192339

Plan Nacional de Desarrollo (PND) 2013-2018 (2013). Programa Nacional Forestal. Especial. https://conamer.gob.mx/documentos/marcojuridico/rev2016/PND%202013-2018.pdf.

Pompa-García, M., Vázquez-Vázquez, L., Zapata-Molina, M., & Solís-Moreno, R. (2012). Modelo conceptual del potencial de incendios forestales en Durango: avances preliminares. Revista mexicana de ciencias forestales, 3(13), 95-106. https://doi.org/10.29298/rmcf.v3i13.492

Rodrígues, R., Torres, R., Matthes, L., & Penha, A. (2004). Tree Species Sprouting from Root Buds in a Semideciduous Forest Affected by Fire. Brazilian Archives of Biology and Technology, 47(1), 127-133. https://doi.org/10.1590/S1516-89132004000100017

Rodriguez Trejo, D. A. (1994). La lucha contra el fuego. Guía para la prevención, presupresión y supresión de incendios forestales. Universidad Autónoma Chapingo.

Rodríguez Trejo, D. A. (2002). Efecto del fuego en el crecimiento en diámetro de Eucalyptus camaldulensis Dehnh. Revista Chapingo. Serie Ciencias Forestales y del Ambiente, 8(1), 71-74. https://www.redalyc.org/articulo.oa?id=62980108

Rodríguez Trejo, D. A. (2015). Incendios de vegetación. Su ecología y manejo. Volumen 2. Biblioteca básica de agricultura. Guadalajara, Jalisco México.

Rodríguez Trejo, D. A., Ramírez, M, H., Tchikoue, H., & Santillán, P. J. (2008). Factores que inciden en la siniestralidad de los incendios forestales. Revista Ciencia Forestal en México, 33(104), 37-58. http://cienciasforestales.inifap.gob.mx/editorial/index.php/forestales/article/view/736/1898. https://doi.org/10.1016/j.jfe.2016.10.002

Rodríguez Trejo, D. A., Rodríguez A, M., Fernández S, F., & Pyne S, J. (2002). Educación e Incendios Forestales. Mundi-prensa.

Rodríguez y Silva, F., & González-Cabán, A. (2016). Contribution of suppression difficulty and lessons learned in forecasting fire suppression operations productivity: A methodological approach. Journal of Forest Economics, 25(1), 149-159. http://dx.doi.org/10.1016/j.jfe.2016.10.002.

Rodríguez y Silva, F. (2019). “Modelo econométrico para el diagnóstico y evaluación de costos en la planificación de quemas prescripciones en el paisaje forestal”. En Armando González-Cabán y José J. Sánchez (Coord.), Quinto Simposio Internacional Sobre Políticas, Planificación, y Economía de los Incendios Forestales: Servicios Ambientales e Incendios Forestales. [Memoria de Simposio]. (pp. 182-183). Servicio Forestal del Departamento de Agricultura. Estados Unidos https://doi.org/10.2737/PSW-GTR-261-ES

Rodríguez, M., Reina, J., & Herrera, L. (2008). Eficiencia de la protección contra incendios forestales en Pinar del Río. Revista Forestal Baracoa, 27(2), 31-37.

Rodríguez, S. F., Molina, M. J.R., Herrera, M. M.A., & Rodríguez, L. J. M. (2013). VISUAL-SEVEIF, una herramienta para la integración de la simulación del comportamiento del fuego y la evaluación económica del impacto de los incendios forestales. En Armando González-Cabán (Coord.), Cuarto Simposio Internacional Sobre Políticas, Planificación, y Economía de los Incendios Forestales: Servicios Ambientales e Incendios Forestales. [Memoria de Simposio] (pp. 180-196). Servicio Forestal del Departamento de Agricultura.

Rodríguez, T. D. A. (1996). Incendios forestales. Universidad Autónoma Chapingo. Multi-Prensa. México.

Salgado, P. A. (2021). Cartografía para modelos combustibles utilizando tecnologías geoespaciales para la predicción de incendios forestales en la Reserva Geobotánica Pululahua. [Tesis de grado, Universidad de las Fuerzas Armadas]. Repositorio Dspace. http://repositorio.espe.edu.ec/xmlui/handle/21000/23764

Schwentesius, R., Vázquez, L. E., Ayala, A. V., Rodríguez, F., Gómez, L., & Cruz, J. A. (2021). Comparación de producción orgánica y convencional en aguacate en Ario de Rosales, Michoacán. En F. Pérez Soto, E. Figueroa Hernández, M. Jiménez García, L. Godínez Montoya, & R. S. García Núñez (Coord.), Producción y Comercialización. Asociación Mexicana de Investigación Interdisciplinaria.

SMN. (2017). Resúmenes mensuales de temperaturas y lluvias. [base de datos]. https://smn.conagua.gob.mx/es/climatologia/temperaturas-y-lluvias/resumenes-mensuales -de-temperaturas-y-lluvias

Urquidi, V. L. (2007). Desarrollo sustentable y cambio global. El colegio de México. https://doi.org/10.2307/j.ctvhn09kv

Urquidi, V. L. (2007). Los desafíos del desarrollo sustentable en la región Latinoamericana. Pp. 63-92. En: Nadal, A. Editor. Desarrollo sustentable y cambio global. Editado por El Colegio de México, A. C. México D. F. ISBN: 968-12-1251-7.

Vargas-Sanabria, D., & Quesada-Román, A. (2018). Influencia geomorfológica en la vulnerabilidad a incendios forestales en el Área de Conservación Guanacaste, Costa Rica. Revista de Ciencias Ambientales, 52(2), 1-15. https://doi.org/10.15359/rca.52-2.1

Vega García, C., Woodard, P. M., Titus, S. J., Adamowicz, W. L., & Lee, B. S. (1999). Dos modelos para la predicción de incendios forestales en Whitecourt Forest, Canada. Canadian Forest Service Publications, 8(1), 5-23. https://cfs.nrcan.gc.ca/publications?id=18697

Ynouye-Francés, M., Ramos-Rodríguez, M. P., Martínez-Becerra, L. W., Cabrera-Reina, J. M., González-Rodríguez, R. & Duany-Dangel, A. (2021). Causalidad de los incendios forestales en Pinar del Río, Cuba (1975-2018). Colombia forestal, 24(2), 24-38. https://doi.org/10.14483/2256201X.16881.

Apéndice 1. Pruebas de estadísticos de bondad del Modelo Estadístico de datos panel con efectos fijos: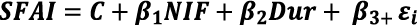

Panel: Efectos fijos, utilizando 242 observaciones

Se han incluido 11 unidades de sección cruzada

Largura de la serie temporal = 22

Variable dependiente: LogSFAI

	Coeficiente		Desv. Típica			Estadístico t		valor p
const	0.197880		0.116827			1.694		0.0917		*
LogNIF	0.991790		0.0339257			29.23		<0.0001		***
LogDur	1.02476		0.0766844			13.36		<0.0001		***
LogTLl	−0.0500872		0.0765667			−0.6542		0.5137
Media de la vble. dep.		3.277097			D.T. de la vble. dep.				0.615625
Suma de cuad. residuos		16.26574			D.T. de la regresión				0.267097
R-cuadrado MCVF (LSDV)		0.821917			R-cuadrado ‘intra’				0.794623
F (13, 228) MCVF		80.94604			Valor p (de F)				1.07e-77
Log-verosimilitud		−16.69805			Criterio de Akaike				61.39610
Criterio de Schwarz		110.2412			Crit. de Hannan-Quinn				81.07267
rho		0.085896			Durbin-Watson				1.733088
Contrastes
Heterocedasticidad libre de distribución de Wald							Normalidad de los residuos
Chi-cuadrado (11) = 39.6885							Chi-cuadrado (2) = 13.442
con valor p = 0.0000404392							con valor p = 0.00120536
Wooldridge de autocorrelación en datos de panel
Estadístico de contraste: F (1, 10) = 2.00206
con valor p = P (F(1, 10) > 2.00206) = 0.187462

Apéndice 2. Pruebas de estadísticos de bondad del Modelo Estadístico de datos panel con efectos fijos: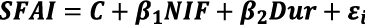

	Coeficiente		Desv. Típica				Estadístico t	valor p
const	0.219579		0.291930				0.7522	0.4693
LogNIF	1.28413		0.0918763				13.98	<0.0001	***
LogDur	0.523415		0.135942				3.850	0.0032	***
Media de la vble. dep.		3.277097			D.T. de la vble. dep.				0.615625
Suma de cuad. residuos		8.042817			D.T. de la regresión				0.196640
R-cuadrado MCVF (LSDV)		0.911944			R-cuadrado ‘intra’				0.898448
Log-verosimilitud		68.52004			Criterio de Akaike				−69.04008
Criterio de Schwarz		49.58381			Crit. de Hannan-Quinn				−21.25411
rho		−0.067306			Durbin-Watson valor p = 0.97874				2.040714
Contrastes
Conjunto de los regresores (excepto la constante)						Heterocedasticidad libre de distribución de Wald
Estadístico de contraste: F (2, 10) = 99.8997						Estadístico de contraste asintótico: Chi-cuadrado (11) = 27.8791
con valor p = P (F(2, 10) > 99.8997) = 0.000000246025						con valor p = 0.00337824
Wooldridge de autocorrelación en datos de panel						Normalidad de los residuos
Estadístico de contraste: F (1, 10) = 0.68531						Hipótesis nula: [El error tiene distribución Normal]
con valor p = P (F(1, 10) > 0.68531) = 0.427079						Estadístico de contraste: Chi-cuadrado (2) = 4.16659
Estadístico de Durbin-Watson = 2.04071; valor p = 0.97874						con valor p = 0.124519

Diagnósticos de colinealidad de Belsley-Kuh-Welsch:

Proporciones de la varianza

lambda cond const LogNIF LogDur

2.773 1.000 0.003 0.005 0.018

0.211 3.629 0.005 0.069 0.474

0.016 13.061 0.992 0.926 0.508

(De acuerdo con BKW, cond >= 30 indica “fuerte” dependencia casi lineal, y cond entre 10 y 30 “moderadamente fuerte”. Cuenta de índices de condición >= 30: 0; Cuenta de índices de condición >= 10: 1; Proporciones de varianza >= 0.5 asociadas con condición >= 10:

const LogNIF LogDur

0.992 0.926 0.508

---

Top