Generación de residuos sólidos urbanos municipales y su relación con un indicador de ingreso municipal en México (años 2010 y 2015)

Generation of municipal urban solid waste and its relationship with an indicator of municipal income in Mexico (years 2010 and 2015)

Sergio Gabriel Ceballos Pérez1, Ramiro Flores-Xolocotzi2

[Recibido: 17 de junio 2022, Aceptado: 11 octubre 2022, Corregido: 21 de octubre 2022, Publicado: 16 de noviembre 2022]

Resumen

[Introducción]: La relación teórica entre crecimiento económico (medido a través de algún indicador de ingreso) y la generación de contaminantes explica que a cierto nivel de crecimiento empieza un decremento de los mismos, proceso conocido como desacoplamiento y que posiblemente indique la presencia de una Curva Ambiental de Kuznets (CAK). [Objetivo]: Se estudió un posible desacoplamiento de residuos sólidos urbanos municipales en México en los años 2010 y 2015 para 2 183 municipios. [Metodología]: Para ello se empleó como variable independiente el ingreso per cápita anual municipal en dólares expresados como paridades de poder de compra. Además, el modelo se controló a través de densidad poblacional y de escolaridad promedio municipales. [Resultados]: Los resultados de modelos estimados por efectos aleatorios, efectos fijos y efectos fijos con errores estándar robustos de clúster evidencian probable desacoplamiento entre ingreso y niveles de residuos sólidos urbanos considerando los 2 183 municipios estudiados. [Conclusiones]: Si bien es posible la existencia de una CAK, son necesarias nuevas investigaciones mexicanas y también latinoamericanas que contrasten dicha hipótesis dentro de un horizonte temporal largo a nivel nacional, regional y sectorial; y contemplar también el efecto de otras variables relacionadas con la recolección de residuos sólidos urbanos y de reciclaje.

Palabras-clave: Contaminación; curva ambiental de Kuznets; datos de panel; efectos fijos.

Abstract

[Introduction]: The theoretical relationship between economic growth (measured through some income indicator) and the generation of pollutants explains that at a certain level of growth, a decrease in them begins, a process known as decoupling and that possibly indicates the presence of an Environmental Curve of Kuznets (CAK). [Objective]: A possible decoupling of municipal solid waste in Mexico was studied for the years 2010 and 2015 in 2 183 municipalities. [Methodology]: For this purpose, the independent variable used was the annual municipal income per capita in dollars expressed as purchasing power parities. In addition, the model was controlled by municipal population density and average municipal schooling. [Results]: The results of models estimated by random effects, fixed effects, and cluster robust standard errors in fixed effects show the probable existence of decoupling between income and municipal solid waste in the 2 183 municipalities studied. [Conclusions]: Although there is a possible CAK, new research is needed to contrast this hypothesis considering a long-time horizon at the national, regional, and sectorial levels in Mexico and Latin America too, as well as considering the effect of variables related to the collection of urban solid waste and recycling.

Keywords: Fixed effects, Kuznets curve; panel data; pollution.

1. Introducción

Los residuos sólidos urbanos en el ámbito municipal (RSUM) resultantes de las actividades de consumo se relacionan con el crecimiento económico de las ciudades, factores poblacionales y su distribución en el espacio (densidad poblacional); y son además determinados por los hábitos de consumo de las personas (Araiza et al., 2017). De esta forma, la generación de RSUM puede ser vista como un costo negativo del consumo de bienes y servicios en hogares, oficinas y espacios públicos donde se desarrollan las actividades cotidianas de las personas. Los RSUM a los que se hará referencia en esta investigación comprenderán únicamente materiales sólidos de desecho que se producen en casas-habitación, además de oficinas, comercios y escuelas, ya sea que puedan reciclarse o no (Araiza et al., 2017; INEGI, 2013). Consecuentemente, este trabajo se enfoca de forma exclusiva al sector económico del consumidor final (en hogares, oficinas, comercios y escuelas). Si bien pudieran incluirse en futuras investigaciones residuos del sector agrícola, residuos peligrosos (de hospitales e industriales) u otros, se tendrían que considerar la posibilidad de que la relación entre las variables de crecimiento económico, ingreso y generación de residuos sea diferente (Dinda, 2004; Dinda, 2005).

Debido al impacto que tienen los RSUM sobre el medioambiente urbano, es necesario identificar la relación funcional causa y efecto entre la emisión de RSUM y el crecimiento económico asociado al auge de las ciudades (Madden et al., 2019; Tsiamis et al., 2018). Para investigar la relación entre la calidad ambiental y el crecimiento económico, se ha empleado la hipótesis de curva ambiental de Kuznets (CAK) (Boubellouta y Kusch-Brandt, 2020; Tsiamis et al., 2018). La hipótesis sostiene que existe una amplia desigualdad en la calidad ambiental en las primeras etapas del crecimiento económico entre las naciones, ciudades o localidades. Posteriormente, según dicha hipótesis, el crecimiento económico llegará a un punto crítico, en donde la desigualdad en la calidad ambiental se reduce conforme el crecimiento continúa (crecimiento expresado a través de un indicador macroeconómico de ingreso). Este proceso es conocido como desacoplamiento y es explicado por la hipótesis de CAK (Boubellouta y Kusch-Brandt, 2020; Jaligot y Chenal, 2018). Desde una perspectiva ambiental, el paradigma de CAK ha desarrollado modelos con indicadores de degradación ambiental (como los RSUM) y medidas de ingreso nacional como el Producto Interno Bruto u otras medidas de ingreso (Boubellouta y Kusch-Brandt, 2020; Jaligot y Chenal, 2018).

De acuerdo con Dinda (2004; 2005), de la relación entre crecimiento económico y emisión de contaminantes, se derivan algunos aspectos que pueden relacionarse con los residuos sólidos:

a)Es más factible que exista una CAK en el caso de contaminantes locales (como contaminantes atmosféricos de una ciudad) que en contaminantes globales (gases que causan efecto invernadero). La solución con respecto a estos últimos implica estrategias y acuerdos internacionales que complican el desarrollo de políticas económicas tendientes a minimizar sus niveles de emisión.

b)La evidencia empírica demuestra que es más factible encontrar una CAK en contaminantes que impactan directamente en la salud humana debido a que son problemas que tienden a disminuir constantemente con el crecimiento económico. Este podría ser el caso de los residuos sólidos peligrosos (hospitalarios e industriales) incluyendo aquellos derivados de la actividad agrícola y de la industria química y farmacéutica (Bustos, 2009). No sería el caso de los RSUM en los cuales se ha observado que tienen una relación monotónica creciente con el ingreso de los consumidores finales en hogares. Según Dinda (2005), cuando los problemas ambientales pueden externalizarse (es el caso de los RSUM), la curva podría ni siquiera descender en los niveles de ingresos altos. Estos argumentos deberán considerarse en futuros estudios que comprendan residuos sólidos totales.

En vista de lo anterior, en este estudio se contrasta econométricamente la relación que pudiera existir entre un indicador macroeconómico de ingreso anual per cápita municipal y los residuos sólidos urbanos municipales (RSUM) considerando las 32 entidades federativas de México a un nivel municipal para los años 2010 y 2015. En consecuencia, el objetivo de este trabajo es determinar cómo es la relación entre las variables anteriores considerando que pudiera ser señal de la posible existencia de una CAK. Además se contemplan como variables de control la densidad poblacional y la escolaridad promedio a nivel municipal. De sustentarse estadísticamente un posible desacoplamiento entre las variables, se analizaría la relación entre RSUM y el indicador de ingreso a nivel municipal tomando en cuenta el punto de inflexión de la curva que expresa gráficamente dicha relación.

2. Marco teórico

Los estudios sobre emisión de contaminantes y su relación con el crecimiento económico, desacoplamiento e hipótesis de CAK se han realizado en países con diferentes niveles de crecimiento económico, empleando indicadores de contaminantes en suelo, agua, o atmósfera (Dinda, 2005; Stern, 2017). El desacoplamiento y la hipótesis de CAK son una propuesta teórica que permite conocer y explicar en qué posible etapa de crecimiento se encuentra una economía en relación con la calidad ambiental. En una primera etapa de desarrollo el sector industrial crece y con ello la explotación de los recursos naturales y la contaminación también (Boubellouta y Kusch-Brandt, 2020). Sin embargo, la hipótesis considera que una vez que la fase de crecimiento industrial es superada, ocurre una inflexión en la curva (desacoplamiento entre la generación de contaminantes y crecimiento económico) (Catalán, 2014).

En dicha inflexión, sectores económicos como el de servicios se desarrollan provocando cambios estructurales que conllevan incrementos en el ingreso per cápita. Los incrementos en el ingreso asociados al crecimiento económico permiten el acceso a actividades relacionadas con educación, investigación científica e innovación tecnológica (Madden et al., 2019; Rosales et al., 2018). En esta etapa y siguiendo a Rosales et al. (2018), los efectos tecnológicos y estructurales en este modelo económico pueden influir en el fortalecimiento de la regulación ambiental al disminuir la degradación y contaminación masiva debido a la práctica de actividades a favor de la calidad ambiental en la economía. De esta forma, los resultados sobre desacoplamiento pudieran variar de acuerdo con la escala territorial-espacial en la que se realice (nacional a local). Aunque también existen otros elementos que pueden influir, tales como: tecnología, educación, políticas comerciales y políticas ambientales (por ejemplo, reciclaje de RSUM), entre otros (Shimamoto, 2019).

Respecto a residuos sólidos, la relación entre generación de RSUM-crecimiento económico, el desacoplamiento y la hipótesis de CAK, los estudios se han implementado en ámbitos municipales, regionales y nacionales, considerando diferentes tipos de residuos sólidos: urbanos, peligrosos, electrónicos, plásticos, entre otros (Boubellouta y Kusch-Brandt, 2020; Jaligot y Chenal, 2018; Madden et al., 2019; Tsiamis et al., 2018; Yilmaz 2020; Zhao et al., 2020). En la Figura 1 se muestra la forma gráfica de una CAK.

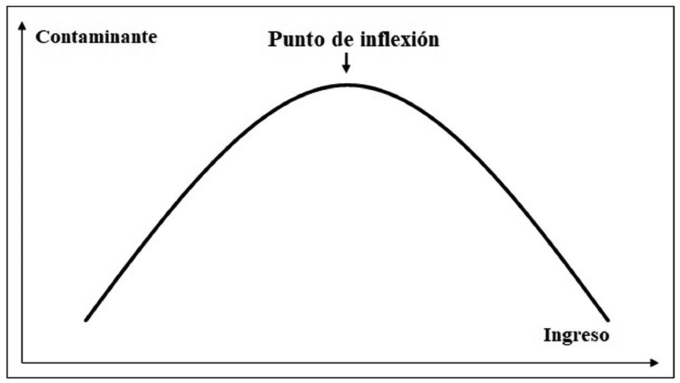
Figura 1. Curva de Kuznets.
Figure 1. Kuznets curve.

La teoría sobre CAK explica la flexión en la curva, considerando los siguientes tres efectos (Zilio y Caraballo, 2014; Stern, 2017; basados a su vez en Grossman y Krueger, 1991):

1)Efecto escala. En esta fase existe un predominio de actividades del sector primario y el sector industrial está en crecimiento. Se caracteriza por presentar, en teoría, una relación positiva entre el crecimiento económico y la degradación ambiental (incrementos en contaminantes). Se interpreta que el deterioro de la calidad ambiental es una característica asociada con el crecimiento económico en las primeras fases del crecimiento económico. El crecimiento se puede medir a través del PIB o de alguna medida de ingreso e incluso se han empleado indicadores de desarrollo sustentable y de desarrollo humano (Akseer y Subhasish, 2021).

2)Efecto tecnología. En esta fase de crecimiento, las economías nacionales alcanzan la capacidad económica para invertir en investigación ambiental, innovación y desarrollo de tecnologías limpias (Dinda, 2005; Stern, 2017) y para el caso de RSUM inversiones en tecnología para reciclaje. Por lo que se empieza a contrarrestar el efecto escala. Existe también un incremento en la conciencia ambiental de los agentes económicos, lo cual puede verse reflejado en su disposición a pagar por una mayor calidad ambiental (Stern, 2017).

3)Efecto composición. Esta fase del crecimiento económico se caracteriza por un predominio del sector terciario (servicios) en el que las innovaciones tecnológicas permiten cambios en los procesos productivos los cuales a su vez mejorarán la calidad ambiental. Por ejemplo a través de reciclaje y valorización
de los RSUM en los ámbitos urbanos. Estos, junto con mecanismos de comando y control (regulación legal de los contaminantes) e instrumentos económicos como impuestos o incentivos relacionados con la emisión de contaminantes como los RSUM, permiten la disminución de los contaminantes (Catalán, 2014).

De acuerdo con Dinda (2005) y Stern (2017), además de estos efectos hay que considerar las hipótesis del desplazamiento y del paraíso contaminante que en conjunto explican la forma en que el comercio internacional puede influir en la relación crecimiento económico-generación de contaminantes. Esta relación permite que los países desarrollados lleven su producción de bienes a economía emergentes con normatividad ambiental laxa, convirtiendo posiblemente a dichas economías en paraísos contaminantes. También hay que considerar que el enfoque de crecimiento económico bajo el que se sustenta la teoría que explica la relación ingreso-contaminante (desacoplamiento y CAK) se basa en la sustitución de capital natural por capital manufacturado (D’Autume y Schubert, 2008; Rodríguez y Ruíz, 2001). Esta viene a ser la base teórica que fundamenta el efecto tecnología y por tanto las propuestas de política pública que promueven el reciclaje y valorización (Brough y Jouhara, 2020; Ibáñez-Forés, et al, 2021). Sin embargo, el reciclaje tiene límites. De acuerdo con Zhou et al. (2019) y Franceschelli, et al. (2019), el reciclaje depende de los tipos de materiales; su reuso requiere de un porcentaje de nuevos materiales y de energía lo cual provoca la existencia de nuevos contaminantes.

Para describir y analizar la probable relación estadística entre generación de RSUM y un indicador de ingreso municipal, esta investigación empleará datos sobre generación de residuos sólidos urbanos a nivel municipal de los años 2010 y 2015 para las 32 entidades federativas mexicanas, incluyendo su capital Ciudad de México (CDMX). Aunque es factible que aparezca un posible indicador de la existencia de una CAK, se deberá considerar que este estudio comprende solo dos anualidades separadas por cinco años mientras que la teoría de CAK comprende tres fases en un horizonte de tiempo que pudiera estar por arriba de cinco años (Stern, 2017). Sin embargo, siguiendo a Halter et al. (2014) sobre la relación entre ingreso y generación de RSU bajo un periodo de tiempo, se debe hacer una diferencia entre evaluar la CAK y evaluar la tendencia de la curva en ese determinado periodo. La idea original de Simón Kuznets, de la cual se derivó la hipótesis de CAK, era conocer la relación entre el ingreso y la disminución de la pobreza sobre periodos de tiempo de largo plazo en los que se puedan observar los cambios estructurales de la economía. No obstante, para el caso de las tendencias, es posible evaluar períodos de tiempo cortos en la curva, lo cual podría manifestar una posible evidencia.

Así pues, la metodología y los resultados de esta investigación deberán leerse dentro del marco descrito. Futuras investigaciones municipales deberán considerar bases de datos continuas en horizontes de tiempo amplios sobre indicadores de ingreso municipal e incluso de PIB municipal. Sin embargo en México no existen dichas bases de datos, amén de que las estadísticas de ingreso municipal que publica INEGI no están completas y son discontinuas (INEGI, 2020).

3. Metodología

3.1 Elaboración de base de datos

Para la realización de la prueba de Kuznets, se emplearon datos sobre generación de residuos sólidos urbanos a nivel municipal (RSUM) de los años 2010 y 2015 para las 32 entidades federativas mexicanas que comprende México, incluyendo su capital CDMX. Los datos de RSUM de 2010, se obtuvieron de los Censos Nacionales de Gobiernos Municipales y Delegacionales realizados por el Instituto Nacional de Estadística y Geografía (INEGI, 2020). Los valores de RSUM de 2015 se obtuvieron estimando una media geométrica con los datos disponibles de forma bianual de 2010, 2012, 2014 y 2016 recopilados de INEGI (2020). Posteriormente se multiplicó por una tasa anualizada con el fin de obtener el valor del 2015 (Ecuación 1) (Kisbye y Levstein, 2010).

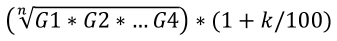(E.1)

Dónde:

G1, G2 hasta G4 es el volumen generado de RSUM bianual para los años 2010, 2012, 2014 y 2016;

n=4 es el número de observaciones, y

k=5 es el año que se desea obtener.

Considerando lo anterior, se obtuvo una base de datos de RSUM para los años 2010 y 2015 que consideró el 88.9 % (N=2 183), de los municipios mexicanos (incluyendo alcaldías en el caso de la Ciudad de México). Se incluyó el total de municipios actualmente existentes en México (INEGI, 2021a). Los municipios que no fueron incluidos fue porque carecían de información anual de 2010 o datos para estimar los RSUM del año 2015.

La información de RSUM obtenida se dividió por la población municipal para los años de estudio. Con ello se obtuvo la variable RSUM per cápita por municipio. Para obtener el número de habitantes por municipio en cada año de estudio se empleó información poblacional de INEGI para los años 2010 y 2015 (INEGI, 2021b).

Siguiendo el modelo económico de la CAK, se empleó como variable económica el “ingreso per cápita anual municipal en dólares expresados en unidades de PPC” (Paridades de Poder de Compra; en adelante variable IMPCC). De acuerdo con INEGI (2021c) las PPC son tipos de conversión de monedas y deflactores espaciales de precios. Su objetivo es eliminar las diferencias en los niveles de precio entre países (valuación al mismo nivel de precio), reflejando diferencias relativas en volúmenes de bienes/servicios comprados en los países. Se empleó IMPPC como variable de ingreso ya que el PIB a nivel municipal en México no existe oficialmente. Sin embargo, el IMPPC cumple con las características de indicador de ingreso para contrastar la hipótesis de Kuznets. Esta medida de ingreso no se deflacta dado que proviene de la Ecuación 2:

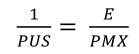(E.2)

En donde PUS representa los niveles de precios extranjeros y PMX el nivel de precios nacional a un determinado año promedio y E el tipo de cambio. En ese sentido, se puede decir que la medida del IMPCC ya se encuentra deflactada (Gómez, 2009).

Los IMPCC de 2010 y 2015 se obtuvieron de las bases de datos del Informe de Desarrollo Humano 2010-2015 desarrollados por el Programa de las Naciones Unidas para el Desarrollo (en adelante PNUD) y cuya información/bases se pueden consultar en línea (PNUD 2021). Igualmente se empleó la variable de densidad poblacional municipal (DPM), dividiendo población anual municipal entre superficie municipal (variable indicadora del grado de urbanización). La superficie municipal se obtuvo de información obtenida y publicada por Pérez (2014) a través del Instituto Nacional de Administración Pública, INAP. También se empleó como variable independiente la escolaridad promedio municipal (EPM) para los años 2010 y 2015 y que es reportada por PNUD (2021). Con estas variables se elaboró una base de datos.

Para cada variable sin transformar, se estimaron promedios (media y mediana), desviación estándar, valor máximo, valor mínimo y valores de asimetría y curtosis. Para el análisis de los modelos se consideraron los signos y la significancia de los parámetros estimados para IMPCCit, y IMPCCit2 (β1 y β2 respectivamente). Las hipótesis a contrastar con los resultados, de acuerdo con Catalán (2014) y Jaligot y Chenal (2018) expresan si existe y cómo es la relación de RSUM con el IMPCC:

Hipótesis 1. β1+β2= 0. No existe relación estadística significativa entre RSUM e IMPCC.

Hipótesis 2. β1> 0 y β2= 0. Existe una relación lineal creciente entre RSUM e IMPCC.

Hipótesis 3. β1< 0 y β2= 0. Posible relación lineal decreciente entre RSUM e IMPCC.

Hipótesis 4. β1> 0 y β2< 0. Probable curva inversa que expresa que ante incrementos en el IMPCC llega un momento en que hay una disminución en la generación de RSUM y que podría ser indicador de una posible CAK.

Hipótesis 5. β1< 0 y β2> 0. Probable curva en forma de U.

3.2 Modelos de regresión

Siguiendo a Jaligot y Chenal (2018), se estimó inicialmente un modelo que contemplara efectos aleatorios (EA) y un modelo que considerara efectos fijos (EF). Si bien las estimaciones por EF y EA consideran heterogeneidad de efectos inobservables, es importante verificar el cumplimiento de supuestos estadísticos de los modelos, dado que si se incumplen pudieran sesgar los parámetros estimados.

En consecuencia, considerando los datos por municipio (N=2 183) en dos períodos de tiempo (2010 y 2015), se aplicaron las pruebas estadísticas de Multiplicadores de Lagrange de Breush-Pagan (Test ML de BP) para seleccionar entre un modelo de efectos aleatorios y un modelo de mínimos cuadrados agrupados (los resultados de este último no se presentan). También un Test Robusto ante posible presencia de heteroscedasticidad basado en el estadístico Sargan-Hansen para seleccionar entre un modelo de EA y EF (Arellano, 1993; Wooldridge, 2010).

Como se verá posteriormente, los resultados de las pruebas estadísticas llevaron a seleccionar el modelo de EF, por lo que se realizaron para el modelo una prueba de Wald modificada para heterocedasticidad grupal (en adelante Test W) (Wooldridge, 2010). Igualmente se optó por analizar solamente la correlación contemporánea (CC) entre las unidades del panel en el modelo de EF. Para analizar la CC se aplicó el test estadístico de Pesaran (Test CCn) (Ditzen, 2018). La prueba contrasta la hipótesis de existencia de CC débil en los paneles “N”. Sobre esto, de acuerdo con Dogan et al. (2020), la presencia de una CC fuerte puede deberse a interacciones y vínculos socioeconómicos entre municipalidades, y, cuyos efectos pueden ser heterogéneos. Dicha heterogeneidad se podría deber a que las unidades de estudio (municipios) tienen diferencias económicas (niveles de crecimiento económico, preponderancia de algún sector económico), sociales (educación) y poblacionales.

Como se comentó anteriormente, la heterogeneidad se considera como parte de los efectos específicos inobservables (constantes en el tiempo) en los modelos de EF y EA (Wooldridge, 2010). Empero, de acuerdo con Freire-Seoane et al. (2020), su efecto implicaría diferentes coeficientes autorregresivos, en este caso para cada municipio. Sin embargo, debido a que los datos consideran sólo dos anualidades (separadas 5 años) es posible soslayar la autocorrelación (correlación serial) en este trabajo (Jaligot y Chenal, 2018; Wooldridge, 2010). Sin embargo, futuras investigaciones de RSUM y crecimiento que empleen series de tiempo deberán considerar la heterogeneidad como parte de los supuestos a evaluar dentro de los modelos, ya que puede derivar en una estimación inconsistente de los parámetros (Dogan et al., 2020).

Como se verá en resultados, las pruebas evidenciaron solo la presencia de heterocedasticidad. Así que se estimó finalmente una regresión de EF con errores estándar robustos de clúster (en adelante EFERC) (Moundigbaye et al., 2018; Wooldridge, 2010). El modelo EFERC permite considerar la presencia de heterocedasticidad en las observaciones a nivel de panel (Moundigbaye et al., 2018; Stata 2019; Wooldridge, 2010).

De acuerdo con lo recomendado por Jaligot y Chenal (2018), el modelo estimado (para EA, EF y EFERC), fue la Ecuación 3, siendo β cada parámetro estimado, en las variables i=municipalidad y t=tiempo (2010 y 2015):

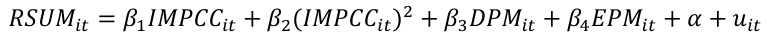(E.3)

En donde:

1.- RSUMit: es la variable dependiente RSUM transformada con LN.

2.- Como variables independientes:

•IMPCCit: Es la variable del ingreso IMPCC anual municipal per cápita en dólares PPC transformada con LN.

•(IMPCCit)2: corresponde al LN del IMPCCit anual municipal per cápita, elevado al cuadrado.

•DPMit: LN de la densidad poblacional municipal.

•EPMit: Escolaridad promedio municipal.

3.- Para la estimación de los modelos, todas las variables (dependiente e independientes) se transformaron con logaritmos naturales (LN) a excepción de la variable EPM (años promedio de escolaridad municipal). Lo anterior se justificó por consideración de que la variable EPM tuvo una curtosis igual a 3 característica de una distribución normal (de 2.99, ver Cuadro 1), aunque su asimetría fue de 0.34. En algunos estudios de CAK algunos investigadores optan por no transformar con logaritmos sus variables en los modelos estimados (Jaligot y Chenal, 2018; Boubellouta y Kusch-Brandt, 2020) o trabajar simultáneamente con variables transformadas y sin transformar considerando las características de cada variable en sus modelos (Fang et al., 2020).

4.- α: se puede entender como un intercepto. Mientras que para efectos fijos α = αi siendo una estimación que absorbe efectos de las variables inobservables que se mantienen constantes en el tiempo (para cada unidad de N) y se correlaciona con las variables independientes.

5.- uit: Es un error aleatorio.

Los modelos se ajustaron en Stata versión 17 (Jaligot y Chenal, 2018).

Finalmente, con los resultados obtenidos se analiza la relación entre RSUM e IMPCC considerando un probable punto de inflexión en la relación entre ambas variables a nivel municipal en las 32 entidades federativas y sus implicaciones a nivel económico-ambiental.

4. Resultados y discusión

4.1 Estadística descriptiva

En el Cuadro 1, se observan los valores promedio de las variables sin transformar con logaritmos de RSUM, IMPCC, DPM y EPM considerando los municipios mexicanos estudiados. Acompañan a estos datos sus correspondientes desviaciones estándar, valores máximos, valores mínimos, asimetrías y curtosis. Se observa que las medianas de RSUM, IMPCC y DPMM son notoriamente inferiores a la media, a excepción de la variable EPM cuya diferencia entre ambas es de 0.15.

Cuadro 1. Estadística descriptiva de las variables sin transformar con logaritmos naturales.
Table 1. Descriptive statistics of variables without transformation with natural logarithms.

Estadístico	RSUM per cápita kg anuales	IMPCC per cápita en dólares PPC	DPM habitantes/km2	EPM, años promedio
Media	220.08	1 855.50	305.16	6.19
Mediana	159.22	1 699.77	57.06	6.04
Desviación estándar	622.69	947.36	1 217.93	1.80
Valor mínimo	0.46	185.29	0.1441	1.05
Valor máximo	25 835.47	9 748.53	17 912.34	12.95
Asimetría	30.12	1.37	8.80	0.34
Curtosis	1084.57	7.43	95.95	2.99

4.2 Modelos estimados y análisis

4.2.1 Estimaciones de efectos aleatorios y efectos fijos

En el Cuadro 2, se observa que la estimación del modelo de efectos aleatorios es estadísticamente significativa al 0.01 de nivel de significancia (NS). El modelo EA demuestra que los términos IMPCCit junto con las variables municipales de densidad poblacional y escolaridad transformadas con logaritmo, son cada una significativas al 0.01 de NS. Los signos asociados a los coeficientes IMPCCit y IMPCCit2 del Modelo EA sustentan la hipótesis 4. (existencia de una probable curva inversa en la relación RSUM con IMPCC). Igualmente, considerando los signos asociados, bajo EA, mayores años de educación promedio municipal se relacionan con mayores cantidades de RSUM. Además se observa una relación inversa entre la densidad poblacional municipal y el RSUM.

El test ML de BP indica que significativamente (NS= 0.01) es mejor optar por un modelo de EA que por los resultados de un modelo de mínimos cuadrados agrupados (cuyos resultados no se presentan en el artículo). Empero, los resultados de la prueba robusta ante heteroscedasticidad basada en el estadístico Sargan-Hansen rechazan significativamente la hipótesis nula que está a favor del modelo de EA, por lo que se sugiere optar por los resultados de EF.

Cuadro 2. Resultados de efectos aleatorios, efectos fijos y efectos fijos con errores estándar de clúster.
Table 2. Random effects, Fixed effects, and cluster standard errors in fixed effects results.

Variable	EA Coeficiente (ee)1	EF Coeficiente (ee)1	EFERC Coeficiente (eerc)2
Constante	-10.57813*** (1.938433)	-1.97594 (3.130742)	-1.97594 (3.605717)
IMPCCit	3.306459*** (0.5313263)	1.727154** (0.8387289)	1.727154* (0.9480924)
IMPCC it2	-0.170388*** (0.0366201)	-0.1090958* (0.0567819)	-0.1090958* (0.064042)
DPMit	-0.028551*** (0.010313)	-0.311138** (0.155987)	-0.311138* (0.1661956)
EPMit	0.080619*** (0.016043)	0.216582** (0.0313703)	0.216582*** (0.0337409)
R2	0.32	0.84	0.84
Test del modelo	Wald=1 340.17***	F=28.23***	F=29.50***
Test ML de BP	576.74***	--------------------	-----------------
Test robusto basado en Sargan-Hansen	108.870***		----------------
Test W Chi2	------	1.29 X 106***	---------------
Test CC(n)	------	-0.897	---------------

*** Indican significancia al 0.01; ** indican significancia al 0.05 y * significancia al 0.1

1ee es el error estándar.

2eerc es el error estándar robusto de clúster.

Siguiendo con EF, los resultados del Test W y del Test CC(n) (Cuadro 2), indican que se rechaza la hipótesis nula de homocedasticidad (NS= 0.01) y no se rechaza ni al 0.1 de NS la hipótesis nula de correlación contemporánea débil, respectivamente. No obstante, el Test W pierde potencia cuando N>T, ante esta advertencia, Wooldridge (2010) sugiere emplear errores estándar robustos cuando T es fijo y N tiende a infinito ante posible presencia de heterocedasticidad. En consecuencia, se presentan en la columna derecha del Cuadro 2, los resultados del modelo de efectos fijos con errores estándar robustos de clúster ante posible presencia de heteroscedasticidad (EFERC). Antes de pasar a su análisis, se señala que los 3 modelos (EA, EF y EFERC) son significativos al 0.01.

Sobre bondad de ajuste (variación explicada de la variable dependiente), considerando el R2, los mejores modelos son EF y EFERC, (Cuadro 2). Además, el valor de los errores estándar tiende a ser mayor, en algunas variables en EF que en EA y finalmente mayor en EFERC que en el modelo EA. Del resto de variables, se observa en los modelos estimados una relación positiva significativa entre RSUM con la variable de escolaridad en el ámbito municipal (al menos con un NS= 0.05). Existiendo también una relación significativa inversa entre la variable de densidad (DPM) y RSUM (al menos con un NS= 0.1).

4.2.2 Modelo con errores estándar robustos de clúster

En los resultados de EFERC (Cuadro 2), se observan los mismos signos que en EF y EA para los parámetros que acompañan a IMPCCit, y IMPCCit2. En el caso de EFERC ambos parámetros son significativos al 0.1 de NS. Por lo que con los resultados de los modelos, y en particular del modelo EFERC, se sustenta la hipótesis 4, que expresa que ante incrementos en el IMPCC llega un momento en que hay una disminución en la generación de RSUM (curva inversa de U) para los municipios bajo estudio en los años 2010 y 2015 (Cuadro 2).

Así, los resultados obtenidos muestran un probable desacoplamiento entre la generación de RSUM y el ingreso en los municipios estudiados. Si bien el resultado es señal de una posible CAK, no se puede concluir que exista debido al horizonte de tiempo empleado, el cual se limitó solo a dos anualidades (2010 y 2015). Por lo que es necesario, que futuras investigaciones sobre RSUM, crecimiento económico y CAK en México consideren un horizonte de tiempo más largo y de preferencia que este sea continuo.

Sobre las variables control, se observa significativamente (NS= 0.1) que incrementos en la densidad municipal se relacionan con decrementos del RSUM. Sobre la relación positiva de RSUM con la variable EPM, (significativa al 0.01 en EA, EF y EFERC); Johnstone y Labonne (2004) y Shimamoto (2019) han estudiado y analizado la existencia de relaciones positivas entre RSUM, con ingreso y escolaridad en otras investigaciones. Esto se podría explicar debido a que mayor escolaridad implica mayores oportunidades de incorporación al mercado laboral y consecuentemente mayores ingresos, mayor consumo y generación de residuos en los hogares (Johnstone y Labonne, 2004; Shimamoto, 2019).

Con respecto a la relación negativa encontrada del RSUM con la densidad poblacional (significativa en los tres modelos con al menos 0.1 de NS) (Cuadro 2), esta se ha analizado como un indicador de urbanización. El signo y significancia encontrada en los diversos estudios es variable (Jaligot y Chenal 2018; Madden et al., 2019). Johnstone y Labonne (2004) y Jaligot y Chenal (2018) mencionan que es posible que la densificación provoque economías de escala en los servicios de recolección de RSUM reduciendo así el costo de la provisión de dichos servicios públicos en las localidades urbanas, incrementando su eficiencia e impactando en menores tasas de generación de RSUM. Sin embargo, la presencia de un eficiente servicio de recolección de residuos no va necesariamente asociado a la presencia de una estrategia política de reciclaje por lo que la densidad podría tener una relación positiva en la generación de RSUM.

Igualmente, Johnstone y Labonne (2004), señalan que es probable que variables como urbanización y densidad poblacional tengan una relación positiva con la generación de RSUM. El argumento que proporcionan es la consideración de que los hogares urbanos tienen menos posibilidades de reúso y reciclaje con respecto a los hogares rurales.

Las variables control empleadas en este trabajo podrían ser consideradas en futuras investigaciones junto con otras características de los hogares municipales (por ejemplo, promedio de personas, promedio de niños, proporción de sexos en casa-habitación e indicadores de calidad de vida). Así, nuevas investigaciones sobre crecimiento económico, RSUM y CAK en México o en otros países latinoamericanos podrían controlar este tipo de variables y determinar su impacto en las tasas de generación de RSUM, considerando como se mencionó anteriormente, un horizonte de tiempo más largo y continuo. Es recomendable también que nuevos modelos comprendan variables relacionadas con políticas públicas sobre reciclaje, reúso de productos y factores que impacten en los hábitos de consumo en los hogares. Y, desde luego, que se analice su impacto en la generación de RSUM.

4.3 Estimación del punto de inflexión e implicaciones

De acuerdo con Chen (2010), si se cumple la hipótesis 4, para estimar el punto de inflexión (PI), entre RSUM e ingreso, se emplean los resultados de los parámetros que acompañan a las variables IMPCCit, y (IMPCCit)2 (β1 y β2 de la Ecuación 4 respectivamente). Para ello se usarán los resultados del modelo EFERC y se recurre a la fórmula:

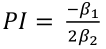(E.4)

Considerando la transformación con logaritmos naturales, se hace la estimación y se obtiene un punto de inflexión de $2 740.149 dólares expresados en unidades de PPC. Dicho punto está por arriba de la media y mediana de IMPCC del conjunto de datos (ver Cuadro 1), pero por abajo del valor máximo de $9 748.53 de IMPCC incluyendo todos los municipios (N= 2 183).

Considerando los 2 183 municipios comprendidos en esta investigación y los IMPCC del año 2015, en el Cuadro 3, se encuentra que 419 de esos municipios al año 2015, en las 32 entidades mexicanas, han superado el punto de inflexión estimado con los resultados del modelo EFERC.

Cuadro 3. Municipios que superan el punto de inflexión por entidad al año 2015
Table 3. Municipalities that exceed the turning point by entity (year 2015)

Entidad	Número de municipios		Tasa de cobertura de PI Respecto a estudiados.	Medianas anuales per cápita municipales 2015
	Supera PI	Estudiados		IMPCC en dólares PPC1	RSUM kg anuales
Ciudad de México	15	15	100.0	4 440.9	602.4
Baja California	5	5	100.0	3 898.3	315.8
Quintana Roo	6	9	66.7	3 662.0	463.7
Baja California Sur	5	5	100.0	3 633.6	515.3
Nuevo León	41	49	83.7	3 460.8	294.8
Sonora	55	71	77.5	3 425.6	260.6
Coahuila	27	36	75.0	3 256.4	281.0
Colima	7	10	70.0	2 925.7	379.3
Sinaloa	8	18	44.4	2 628.1	329.0
Jalisco	52	124	41.9	2 608.8	305.4
Nayarit	6	20	30.0	2 464.5	339.2
Tabasco	4	17	23.5	2 418.9	283.2
Morelos	9	33	27.3	2 412.6	220.4
Querétaro	6	18	33.3	2 412.1	225.2
Chihuahua	17	58	29.3	2 364.8	224.6
Campeche	2	11	18.2	2 354.8	241.1
Aguascalientes	3	11	27.3	2 303.2	241.7
Durango	5	37	13.5	2 230.2	180.4
México	26	120	21.7	2 228.0	213.4
Tlaxcala	5	60	8.3	2 151.1	235.8
Guanajuato	7	44	15.9	2 151.1	247.0
Tamaulipas	13	40	32.5	2 073.9	251.9
Hidalgo	14	80	17.5	1 972.7	174.0
Yucatán	14	106	13.2	1 970.2	128.6
Zacatecas	3	56	5.4	1 882.7	279.7
Michoacán	5	112	4.5	1 771.1	233.9
San Luis Potosí	4	58	6.9	1 719.9	148.4
Veracruz	20	166	12.0	1 704.4	155.9
Guerrero	3	80	3.8	1 456.0	111.0
Puebla	3	207	1.4	1 416.6	127.9
Chiapas	2	117	1.7	1 169.5	120.0
Oaxaca	27	390	6.9	1 112.8	59.6

1El Cuadro se ordena de mayor a menor IMPCC y en negrilla se encuentran los porcentajes de cobertura mayores a 50 % con sus correspondientes IMPCC.

El Cuadro 3, considera número de municipios por entidad federativa que han rebasado el punto de inflexión al año 2015. Para enriquecer el análisis de política ambiental y económica, del lado derecho se reportan valores promedio de IMPCC y RSUM. Igualmente, las entidades se ordenan de mayor a menor IMPCC promedio. Debido a la asimetría de las variables IMPCC y RSUM se emplean las medianas como indicadores del promedio.

Considerando la tasa de cobertura del PI de los municipios a nivel estatal, las mayores tasas corresponden a Ciudad de México, Baja California y Baja California Sur con 100 % y las menores tasas corresponden a Oaxaca y San Luis Potosí (6.9 %); Zacatecas (5.4 %); Michoacán (4.5 %); Guerrero (3.8 %); Chiapas (1.7 %) y Puebla (1.4 %). Se hace la observación de que, en el caso de la Ciudad de México, esta investigación no comprendió una de sus 16 alcaldías: Benito Juárez. Pero en el caso de Baja California y Baja California Sur todos los municipios están representados.

En el Cuadro 3 se observa que las ocho entidades que rebasan un 50 % tasa de cobertura del PI coinciden en ser las 8 entidades con los mayores niveles de ingreso per cápita (IMPCC) promedio (considerando la mediana) a nivel nacional. Dichas entidades son, en orden decreciente de IMPCC: Ciudad de México, Baja California, Quintana Roo, Baja California Sur, Nuevo León, Sonora, Coahuila y Colima. Para poner en perspectiva de análisis se señala lo siguiente.

El Cuadro 3 muestra que la Ciudad de México, Baja California Sur y Quintana Roo (de las 8 entidades ya mencionadas) si bien son entidades con alto porcentaje de cobertura (del PI) con respecto a municipalidades estudiadas, son las entidades con mayores niveles per cápita de RSUM en términos de la mediana con 602.4, 515.3 y 463.7, respectivamente. Si se consideran que las medianas nacionales per cápita municipales de IMPCC y RSUM al año 2015, fueron de 1 876.22 y 172.33 respectivamente, entonces 7 entidades (Michoacán, San Luis Potosí, Veracruz, Guerrero, Puebla, Chiapas y Oaxaca) de las 24 restantes, están por debajo de la mediana nacional 2015 de IMPCC y con coberturas de PI que van de 1.4 % en Puebla a 12 % en Veracruz.

Siguiendo con RSUM (Cuadro 3), también 7 entidades están por debajo de la mediana nacional 2015 (Yucatán, San Luis Potosí, Veracruz, Guerrero, Puebla, Chiapas y Oaxaca) con coberturas de PI de 1.4 de Puebla a 13.2 % de Yucatán.

De lo anterior se desprende que las entidades con mayores tasas de cobertura de PI tienden a ser entidades con mayores cantidades municipales per cápita promedio de IMPCC y de RSUM. Al respecto, según los datos del Cuadro 3 (32 entidades): coeficientes de correlación de Spearman estimados entre tasa de cobertura con IMPCC, tasa de cobertura con RSUM y RSUM con IMPCC tienen valores de 0.94, 0.81 y 0.87 respectivamente (todos significativos al 0.01). Lo anterior indica una asociación directa positiva en los pares de variables: incrementos en una variable se asocian con incrementos en la otra y decrementos de una variable se asocian a decrementos en la otra.

Hay que señalar también que las alcaldías de la Ciudad de México se caracterizan por la preponderancia del sector terciario basado en servicios, incluyendo el turismo para el caso particular de Baja California, Baja California Sur y Quintana Roo (Sánchez-Crispín y Propin-Frejomil, 2011). Mientras que las entidades con menores tasas de cobertura como Oaxaca, Guerrero y Chiapas se caracterizan por ser entidades con preponderancia del sector primario (agricultura y ganadería) (Rodríguez-Hernández et al., 2016).

Fuera del grupo de municipios del Cuadro 3, existe un conjunto amplio de municipalidades (1 764) que de acuerdo con los resultados aquí obtenidos no han alcanzado el punto de inflexión. Bajo la observación de que esta investigación está acotada sólo a dos anualidades (2010 y 2015), la relación entre generación de contaminantes y crecimiento económico se pudiera explicar por los efectos escala, tecnología y composición. El primero hace referencia a economías basadas en el sector primario y en fase temprana de crecimiento; el segundo hace referencia a economías en donde el crecimiento incentiva la innovación tecnológica (tecnologías de reciclaje y de control de contaminantes) y un mayor interés ecológico-ambiental. Mientras que la tercera fase es producto del crecimiento, resultando en una disminución de los contaminantes ante este (punto de inflexión) (Catalán 2014).

Consecuentemente, a nivel de política pública, se observa que, bajo la relación ingreso-generación de RSUM en las dos anualidades estudiadas, la mayoría de los municipios no han alcanzado el punto de inflexión. Esto significa que sería necesario desarrollar estrategias a nivel nacional dirigidas a innovaciones tecnológicas para el manejo y reciclaje de RSUM a la par del crecimiento económico de las municipalidades (Johnstone y Labonne, 2004). Además del cumplimiento de la normatividad legal necesaria para el manejo de RSUM en sitios de confinamiento y de rellenos sanitarios en los municipios, es necesario incentivar a nivel de municipalidad el desarrollo de una fase de innovaciones tecnológicas para el reciclaje de RSUM, tal como se está llevando a cabo en otras partes del mundo (Johnstone y Labonne, 2004; Jaligot y Chenal, 2018).

Estas recomendaciones podrían extenderse a América Latina y a economías emergentes, en donde desafortunadamente no se han desarrollado estudios macroeconómicos de desacoplamiento entre generación de RSUM e Ingreso; además de desarrollar investigaciones que contrasten econométricamente la hipótesis de CAK. En consecuencia, es necesario que se desarrollen investigaciones macroeconómicas de RSUM y de crecimiento económico en la región latinoamericana a nivel nacional, estatal o municipal, considerando horizontes extensos de tiempo.

Finalmente, aunque los resultados de esta investigación demuestran un probable desacoplamiento entre generación de RSUM y un indicador de Ingreso en municipios, los resultados expuestos no son concluyentes en cuanto a la existencia de una CAK debido a la delimitación temporal (T=2 años, 2010 y 2015) y de municipios contemplados (N=2 183, 88.9 % de municipalidades mexicanas). Futuras investigaciones nacionales, regionales y sectoriales (por ejemplo, turismo) podrían analizar la CAK y contrastar su hipótesis considerando un panel de emisión de RSUM con un horizonte de tiempo largo y pasar de un análisis estático a un análisis dinámico. Se hace necesario que la generación de estadísticas sobre tasas de emisión de RSUM se hagan de manera continua y estable. Empero, este trabajo constituye un avance sobre la emisión de RSUM en México y arroja evidencia sobre un probable desacoplamiento económico entre los RSUM y un indicador de ingreso per cápita municipal.

5. Conclusiones

Considerando los datos del 88.9 % de municipios mexicanos en los años 2010 y 2015, la hipótesis que explica la relación entre generación de RSUM con niveles de ingreso sustenta un posible desacoplamiento. Lo anterior se explica mediante los signos obtenidos en los coeficientes de las variables de ingreso: IMPCCit (NS=0.1) e IMPCCit2 (NS=0.1) en el modelo estimado con errores estándar robustos de clúster (modelo EFERC). El comportamiento de los signos para ambas variables (IMPCCit, IMPCCit2) se observa también en los resultados de EA y de EF. Sin embargo, ante posible presencia de heterocedasticidad se opta por emplear los resultados del modelo EFERC. No obstante, se destaca que el modelo está limitado sólo a dos anualidades separadas cinco años una de otra, por lo que si bien los resultados son señal de la posible existencia de una CAK, estudios futuros deberán considerar un horizonte temporal continuo más amplio que permita contrastar la hipótesis de CAK relacionando generación de RSUM con ingresos.

A partir de los resultados del modelo EFERC respecto a las variables control, se concluye que existe una probable relación negativa entre RSUM y la variable de densidad poblacional, además de existir una probable relación positiva entre RSUM y la variable de escolaridad promedio municipal.

Con los resultados del modelo seleccionado se obtiene un PI de 2 740.149 dólares expresados en unidades de PPC. Con este valor se encuentra que 419 de esos municipios al año 2015 en las 32 entidades mexicanas superan el punto de inflexión. Se encontró que ocho entidades que rebasan en un 50 % la tasa de cobertura del PI son las 8 entidades con los mayores niveles de ingreso per cápita (IMPCC) a nivel nacional a 2015. Dichas entidades son Ciudad de México, Baja California, Quintana Roo, Baja California Sur, Nuevo León, Sonora, Coahuila y Colima.

Igualmente se observa que las menores tasas de cobertura corresponden a Oaxaca y San Luis Potosí (6.9 %); Zacatecas (5.4 %); Michoacán (4.5 %); Guerrero (3.8 %); Chiapas (1.7 %) y Puebla (1.4 %). Varias de estas entidades tienen los menores niveles de ingreso per cápita. En el caso de Oaxaca, Guerrero y Chiapas son entidades federativas mexicanas con preponderancia del sector primario.

A nivel de política pública, teniendo en cuenta que la mayoría de los municipios mexicanos no han alcanzado el punto de inflexión, es necesario que a nivel gubernamental se incentive el desarrollo de innovaciones tecnológicas en el área de gestión y reciclaje de RSUM paralelamente al crecimiento económico de las municipalidades. Estas recomendaciones se pueden extender a otras naciones latinoamericanas en donde las investigaciones sobre RSUM y crecimiento económico son escasas.

6. Agradecimientos

Agradecemos a la Revista y a las personas revisoras anónimas por los comentarios y sugerencias realizados a la versión final del manuscrito.

7. Ética y conflicto de intereses

Los autores de este trabajo declaran haber cumplido con todos los requisitos éticos y legales durante la elaboración del estudio y en la elaboración del manuscrito. No tenemos conflicto de intereses de ningún tipo. No recibimos ningún financiamiento para la investigación ni para la preparación del manuscrito.

8. Referencias

Akseer H., & Subhasish D. (2021). Revisiting environmental Kuznets curve with HDI: New evidence from cross-country panel data. Journal of Environmental Economics and Policy, https://doi.org/10.1080/21606544.2021.1880486

Araiza, J., Chávez, J. y Moreno, J. (2017). Cuantificación de residuos sólidos urbanos generados en la cabecera municipal de Berriozábal, Chiapas, México. Revista Internacional de Contaminación Ambiental, 33(4), 691-699. https://doi.org/10.20937/RICA.2017.33.04.12

Arellano, M. (1993). On the testing of correlated effects with panel data. Journal of Econometrics, 59(1), 87-97. https://doi.org/10.1016/0304-4076(93)90040-C

Ayala S. (2020). Estadística, media geométrica. Escuela Superior Tepeji del Río, Universidad Autónoma del Estado de Hidalgo. https://www.uaeh.edu.mx/division_academica/educacion-media/repositorio/2010/6-semestre/estadistica/media-geometrica.pdf

Boubellouta, B., y Kusch-Brandt, S. (2020). Testing the Environmental Kuznets Curve hypothesis for E-waste in the EU28+2 countries. Journal of Cleaner Production, 277, 1-11. https://doi.org/ 10.1016/j.jclepro.2020.123371

Brough, D. y Jouhara, H. (2020). The aluminium industry: A review on state-of-the-art technologies, environmental impacts and possibilities for waste heat recovery. International Journal of Thermofluids, 1, 1-39. https://doi.org/10.1016/j.ijft.2019.100007

Bustos, C. (2009). La problemática de los desechos sólidos. Economía, 27, 121-144. https://www.redalyc.org/pdf/1956/195614958006.pdf

Catalán, H. (2014). Curva ambiental de Kuznets: Implicaciones para un crecimiento sustentable. Economía Informa, 389, 19-37. https://doi.org/10.1016/S0185-0849(14)72172-3

Chen, C. (2010). Spatial inequality in municipal solid waste disposal across regions in developing countries. International. Journal of Environmental Science and Technology, 7(3), 447–456. https://doi.org/10.1007/BF03326154

D’Autume, A. y Schubert, K. (2008). Zero discounting and optimal paths of depletion of an exhaustible resource with an amenity value. Revue d’Economie Politique, 118(6), 827–845. https://doi.org/10.3917/redp.186.0827

Dinda, S. (2004). Environmental Kuznets Curve Hypothesis: A Survey. Ecological Economics, 49(4), 431-455. https://doi.org/10.1016/j.ecolecon.2004.02.011

Dinda, S. (2005). A theoretical basis for the environmental Kuznets curve. Ecological Economics, 53(3), 403-413. https://doi.org/10.1016/j.ecolecon.2004.10.007

Ditzen, J. (2018). Estimating Dynamic Common-Correlated Effects in Stata. The Stata Journal: Promoting Communications on Statistics and Stata, 18(3), 585–617. https://doi.org/10.1177/1536867x1801800306

Dogan, E., Ulucak, R., Kocak, E. e Isik, C. (2020). The use of ecological footprint in estimating the Environmental Kuznets Curve hypothesis for BRICST by considering cross-section dependence and heterogeneity. Science of The Total Environment, 723, 1-9. https://doi.org/10.1016/j.scitotenv.2020.138063

Fang, Z, Huang, B. y Yang, Z. (2020). Trade openness and the environmental Kuznets curve: Evidence from Chinese cities. The World Economy, 43, 2622-2649. https://doi.org/10.1111/twec.12717

Franceschelli, M., Santoro, G., Giacosa, E. y Quaglia, R. (2019). Assessing the determinants of performance in the recycling business: Evidence from the Italian context. Corporate Social. Responsibility and Environmental Management, 26(5), 1086-1099. https://doi.org/10.1002/csr.1788

Freire-Seoane, M. López-Bermúdez, B. y De la Peña, I. (2020). Efectos del transporte marítimo en contenedores sobre el crecimiento económico en los países de la costa oeste de América Latina. Revista de la CEPAL, 130, 91-108. https://doi.org/10.18356/f8ba8bbf-es

Gómez, M. (2009). La paridad del poder de compra: Una revisión crítica, Revista nicolaíta de estudios económicos de la Universidad Michoacana de San Nicolás de Hidalgo, 4(2), 89-112. https://biblat.unam.mx/es/revista/revista-nicolaita-de-estudios-economicos/articulo/la-paridad-del-poder-de-compra-una-revision-critica

Grossman, G., & Krueger A. (1991). Environmental Impacts of a North American Free Trade Agreement. National Bureau of Economic Research, Working Paper num. 3914. https://econpapers.repec.org/paper/nbrnberwo/3914.htm

Halter, D., Oechslin, M. y Zweimüller, J. (2014). Desigualdad y crecimiento: La dimensión temporal desatendida. Revista de crecimiento económico, 19(1), 81-104. https://doi.org/10.1007/s10887-013-9099-8

Ibáñez-Forés, V., Coutinho-Nóbrega, C., Guinot-Meneu, M., y Bovea, M. (2021). Achieving waste recovery goals in the medium/long term: Eco-efficiency analysis in a Brazilian city by using the LCA approach. Journal of Environmental Management, 298. https://doi.org/10.1016/j.jenvman.2021.113457

INEGI (2013). Censo Nacional de Gobiernos Municipales y Delegacionales 2013. Memoria de actividades. INEGI. https://www.inegi.org.mx/contenidos/productos/prod_serv/contenidos/espanol/bvinegi/productos/censos/justicia/2013/CNGMD_2013/702825063504.pdf

INEGI (2020). Censo Nacional de Gobiernos Municipales y Demarcaciones Territoriales/Delegacionales, 2011, 2013, 2015, 2017, 2019. INEGI. https://www.inegi.org.mx/programas/cngmd/2019/#Tabulados

INEGI (2021a). Catálogo único de claves de áreas geoestadísticas estatales, municipales y localidades. INEGI. https://www.inegi.org.mx/app/ageeml/

INEGI (2021b). Censos y conteos de población y vivienda. INEGI. https://www.inegi.org.mx/datos/?ps=Programas

INEGI (2021c). Estudios de precios para el Programa Eurostat-OCDE de Paridades de Poder de Compra, Documento Metodológico. INEGI. https://www.inegi.org.mx/contenidos/programas/ppc/2017/documento_metodologico_ppc.pdf

Jaligot, R., & Chenal, J. (2018). Decoupling municipal solid waste generation and economic growth in the canton of Vaud, Switzerland. Resources, Conservation and Recycling, 130, 260–266. https://doi.org/10.1016/j.resconrec.2017.12.014

Johnstone, N., & Labonne, J. (2004). Generation of household solid waste in OECD countries: an empirical analysis using macroeconomic data. Land Economics, 80(4), 529-538. https://doi.org/10.2307/3655808

Kisbye P. y Levstein F. (2010). Todo lo que usted quiere saber de matemática financiera pero no se anima a preguntar. Colección Ciencias Naturales y Matemática. Instituto Nacional de Educación Tecnológica, Buenos Aires Argentina. https://revistas.unc.edu.ar/index.php/REM/article/view/15776

Madden, B., Florin, N., Mohr, S. y Giurco, D. (2019). Using the waste Kuznets’s curve to explore regional variation in the decoupling of waste generation and socioeconomic indicators. Resources, Conservation and Recycling, 149, 674–686. https://doi.org/10.1016/j.resconrec.2019.06.025

Moundigbaye, M., Rea, W. y Reed, R. (2018). Which panel data estimator should I use? A corrigendum and extension. Economics, 12(1), 1-32. https://doi.org/10.5018/economics-ejournal.ja.2018-4

Pérez, F. (2014). Tipología del municipio mexicano para su desarrollo integral. INAP.

PNUD (2021). Informe de desarrollo humano 2010-2015. Transformando México desde lo local Programa de las Naciones Unidas para el Desarrollo, (Bases de Datos). PNUD. https://www.mx.undp.org/content/mexico/es/home/library/poverty/informe-de-desarrollo-humano-municipal-2010-2015--transformando-.html

Rodríguez-Hernández, R., Morales-Guerra, M., Sánchez-Vásquez, V., Cadena-Iñiguez, P., Rendón-Medel, R., (2016). Vinculación al mercado y competitividad de unidades campesinas en situación de pobreza en Oaxaca, Guerrero y Chiapas. Revista Mexicana de Ciencias Agrícolas, 1(15), 3115-3128. https://doi.org/10.29312/remexca.v0i15.430

Rodríguez, L. y Ruiz, D. (2001). El concepto de capital natural en los modelos de crecimiento exógeno. Análisis Económico, 16(33), 109-128. https://www.redalyc.org/pdf/413/41303304.pdf

Rosales, A.; Kwon, N. y Quintana-Romero, L. (2018). El tamaño de las empresas manufactureras y la contaminación medioambiental en México: Una aproximación espacial. EURE 44(131), 1-22. http://dx.doi.org/10.4067/S0250-71612018000100075

Sánchez-Crispín, Á., y Propin-Frejomil, E. (2011). Transporte y turismo en la península de Baja California, México. Revista Transporte y Territorio, 1(5) 48-71. http://revistascientificas.filo.uba.ar/index.php/rtt/article/view/266

Shimamoto, K. (2019). Determining factors of waste management in Japan. Theoretical and Empirical Research in Urban Management, 14(3), 62-76. https://www.jstor.org/stable/e26753784

Stata (2019). Stata longitudinal data/panel data reference Manual Release 16. Stata Press. https://www.stata.com/manuals/xt.pdf

Stern, D. (2017). The environmental Kuznets curve after 25 years. Journal of Bioeconomics, 19, 7–28. https://doi.org/10.1007/s10818-017-9243-1

Tsiamis, D., Torres, M. y Castaldi, M. (2018). Role of plastics in decoupling municipal solid waste and economic growth in the U.S. Waste Management, 77, 147–155. https://doi.org/10.1016/j.wasman.2018.05.003

Wooldridge, J. (2010). Econometric analysis of cross section and panel data. MIT Press.

Yilmaz, F. (2020). Is there a waste Kuznets curve for OECD? Some evidence from panel analysis. Environmental Science and Pollution Research, 27(32), 40331–40345. https://doi.org/10.1007/s11356-020-09109-0

Zhao, Z., Zou, J., & Zhang, Z. (2020). Does China’s municipal solid waste source separation program work? Evidence from the spatial-two-stage-least squares models. Sustainability, 12, 1-20. https://doi.org/10.3390/su12041664

Zhou, F., Lim, M., He, Y., Lin, Y., & Chen, S. (2019). End-of-life vehicle (ELV) recycling management: Improving performance using an ISM approach. Journal of Cleaner Production, 228, 231-243. https://doi.org/10.1016/j.jclepro.2019.04.182

Zilio, M. y Caraballo, M. (2014). ¿El final de la curva de Kuznets de carbono? Un análisis semiparamétrico para la América Latina y el Caribe. El Trimestre Económico, 81(321), 241-270. https://doi.org/10.20430/ete.v81i321.114

---

Top