
Revista Economía y Sociedad
EISSN: 2215-3403
Número 54 Julio-diciembre 2018
Páginas de la 27 a la 48 del documento impreso
 |
Revista Economía y Sociedad EISSN: 2215-3403 Número 54 Julio-diciembre 2018 Páginas de la 27 a la 48 del documento impreso |
CAMBIO TECNOLÓGICO ENDÓGENO Y TASA DE INTERÉS EN LA DINÁMICA DE LA GLOBALIZACIÓN1
ENDOGENOUS TECHNOLOGICAL CHANGE AND INTEREST RATE IN THE DYNAMICS OF GLOBALIZATION
MUDANÇA TECNOLÓGICA ENDÓGENA E OS JUROS NA DINÂMICA DA GLOBALIZAÇÃO
Mario Eduardo Firmenich2
Doi: http://dx.doi.org/10.15359/eys.23-54.2
Resumen
El crecimiento económico global ha sido entendido en las últimas décadas desde la perspectiva neoclásica de la Nueva Teoría del Crecimiento, la cual tiene un soporte seminal en Romer (1990). En este trabajo, en primer lugar, se analiza el modelo de Romer (1990) y se demuestra que algunos supuestos neoclásicos generan inconsistencias matemáticas.
En segundo lugar, para evitar los resultados autocontradictorios, se reemplaza los supuestos cuestionados por definiciones y conceptos teóricos no neoclásicos, lo cual implica construir un nuevo modelo transformado. Luego, se define algunos hechos estilizados de la globalización y se testea la capacidad explicativa del modelo transformado, al interpretar dichos hechos desde esta nueva perspectiva.
La conclusión es que mejora la capacidad explicativa si el modelo teórico tiene las siguientes propiedades: a) no existe retorno endógeno al crecimiento equilibrado, b) no existe convergencia automática global en renta per cápita; c) el dinero y la tasa de interés, definidos en unidades monetarias fiduciarias, son gestionados políticamente; d) las preferencias temporales dependen de las expectativas sobre el futuro y e) la globalización financiera no es un mercado competitivo.
Palabras clave: crecimiento endógeno; globalización; tasa de interés; producto marginal del capital
Abstract
Global economic growth has been understood in recent decades from the neoclassical perspective of the New Growth Theory, which has a seminal support in Romer (1990). In this paper, firstly, the Romer model (1990) is analyzed and it is proved that some neoclassical assumptions generate mathematical inconsistencies.
Secondly, to avoid self-contradictory results, the questioned assumptions are replaced by non-neoclassical theoretical definitions and concepts, which implies constructing a new transformed model. In addition, some stylized facts of globalization are defined and the explanatory capacity of the transformed model is tested, by interpreting such facts with this new perspective.
The conclusion is that the explanatory capacity improves if the theoretical model has the following properties: a) there is no endogenous return to balanced growth, b) there is no global automatic convergence in per capita income; c) money and interest rate, defined in fiduciary monetary units, are managed politically; d) temporary preferences depend on expectations about the future; and e) financial globalization is not a competitive market.
Keywords: endogenous growth; globalization; interest rate; marginal product of capital
Resumo
O crescimento econômico global tem sido entendido nas últimas décadas a partir da perspectiva neoclássica da Nova Teoria do Crescimento, que tem um apoio seminal em Romer (1990). Neste trabalho, em primeiro lugar, analisa-se o modelo de Romer (1990) e mostra-se que alguns pressupostos neoclássicos geram inconsistências matemáticas.
Em segundo lugar, para evitar resultados autocontraditórios, substituem-se as suposições questionadas por definições e conceitos teóricos não neoclássicos, o que implica a construção de um novo modelo transformado. Então, definem-se alguns fatos estilizados da globalização e testa-se a capacidade explicativa do modelo transformado, quando se interpreta os fatos a partir desta nova perspectiva.
A conclusão é que há uma melhoria na capacidade explicativa se o modelo teórico tiver as seguintes propriedades: a) a inexistência de um retorno endógeno ao crescimento equilibrado; b) a inexistência da convergência automática global na renda per capita; c) o dinheiro e a taxa de juros, definidos em unidades monetárias fiduciárias, administrados politicamente; d) as preferências temporárias dependem das expectativas sobre o futuro e e) a globalização financeira não é um mercado competitivo.
Palavras-chaves: crescimento endógeno; globalização; taxa de juros; produto marginal do capital
Fecha de recepción: 2-6-2018. Fechas de reenvíos: 6-8-2018, 29-8-2018, 10-9-2018. Aceptado el 14-9-2018. Publicado el 17-9-2018.
1. Introducción
El crecimiento económico global ha sido entendido en las últimas décadas desde la perspectiva neoclásica de la Nueva Teoría del Crecimiento. Esta teoría tiene un soporte seminal en Romer (1990).
Este trabajo analiza críticamente los fundamentos teóricos de dicho modelo y sugiere algunas modificaciones que cambian la perspectiva de interpretación y las conclusiones sobre la dinámica de la globalización. El escrito está organizado del siguiente modo:
En el apartado 2, se expone el sistema de ecuaciones del modelo de Romer (1990).
En el apartado 3, el análisis de este modelo demuestra que, en Romer (1990), el supuesto neoclásico usual de que el producto marginal del capital (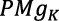 ) es igual a la tasa de interés (r) genera inconsistencias.
) es igual a la tasa de interés (r) genera inconsistencias.
En el apartado 4, se abandona el supuesto 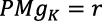 y también que la tasa de descuento del consumo
y también que la tasa de descuento del consumo 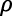 es un parámetro constante. Se introduce en reemplazo supuestos, no neoclásicos.
es un parámetro constante. Se introduce en reemplazo supuestos, no neoclásicos.
En el apartado 5, se analiza las relaciones entre política monetaria y cambio tecnológico endógeno en el modelo transformado con supuestos no neoclásicos.
En el apartado 6, se considera las relaciones entre la globalización financiera y el crecimiento endógeno nacional, al enfatizar las consecuencias para algunos Países Menos Desarrollados (PMDs) de un crecimiento equilibrado en los Países Industrializados (PIs) con una revolución tecnológica endógena y una tasa de interés global muy baja.
En el apartado 7, se definen algunos hechos estilizados de la dinámica de la globalización en las últimas décadas, a los cuales se les da una interpretación plausible con el modelo teórico modificado con supuestos no neoclásicos.
Finalmente se expone como conclusión que la sustitución de algunos supuestos neoclásicos por los conceptos teóricos introducidos en el apartado 4 mejora la capacidad explicativa de los hechos planteados.
2. El sistema de ecuaciones del modelo de Romer (1990)3
Existen 4 inputs: capital x(i), trabajo L supuesto constante, capital humano H supuesto constante y un índice del nivel tecnológico A, que es el número de diseños existentes de bienes de capital, cuyo crecimiento es ilimitado (Romer, 1990, p. 78-79); el número i = A indica las cantidades de bienes de capital en producción y uso, cada uno de ellos es producido por una empresa monopolista; “se supone que los bienes duraderos no se deprecian” (Romer, 1991, p. 454), tienen durabilidad infinita y no sufren obsolescencia. A no puede disminuir.
Dice que: En esta clase de ambiente una forma funcional sencilla para el producto es la extensión siguiente de la función de producción de Cobb-Douglas:
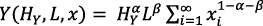 ” (Romer, 1991, p. 453) (1)4
” (Romer, 1991, p. 453) (1)4
Debido al supuesto de simetría, resulta (Romer, 1990, p. 89):
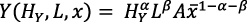 (1 bis)
(1 bis)
Define una medida contable de la acumulación de capital (Romer, 1990, p. 82):
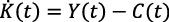 (2)
(2)
La relación de K con los bienes durables usados en la producción es:
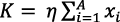 (3)
(3)
Debido a la simetría, resulta (Romer, 1990, p. 89):
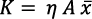 (3 bis)
(3 bis)
η es un parámetro (Romer, 1990, p. 93).
El productor de cada x(i) es un monopolista propietario de una patente. Cualquiera puede usar el conocimiento patentado para producir nuevo conocimiento porque el conocimiento es un insumo no rival (Romer, 1990, p. 83).
Agrega:
(…) se puede derivar la demanda agregada de bienes duraderos a partir de un problema de maximización (…) 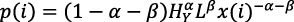 (…) La curva de demanda agregada de [esta] ecuación es lo que toma como dado el productor de cada bien duradero especializado al escoger el precio maximizador de la ganancia que habrá de fijarse. (…) una empresa que ya ha incurrido en la inversión de costo fijo en un diseño escogerá un nivel de producto x para maximizar su ingreso menos el costo variable en cada fecha:
(…) La curva de demanda agregada de [esta] ecuación es lo que toma como dado el productor de cada bien duradero especializado al escoger el precio maximizador de la ganancia que habrá de fijarse. (…) una empresa que ya ha incurrido en la inversión de costo fijo en un diseño escogerá un nivel de producto x para maximizar su ingreso menos el costo variable en cada fecha:
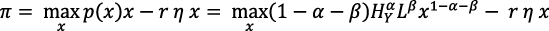 . (Romer, 1991, p. 460).
. (Romer, 1991, p. 460).
r es la tasa de interés de los préstamos denominados en bienes (Romer, 1990, p. 85).
De esta maximización se deduce la cantidad del equilibrio monopólico, ecuación que Romer (1990) no explicita:
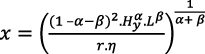 (4)
(4)
Dada la simetría, todos los bienes duraderos se proporcionan al mismo nivel 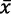 (Romer, 1990, p. 88).
(Romer, 1990, p. 88).
Al sustituir la ecuación (4) en la demanda inversa de x(i) (sin explicitar esta deducción) se halla el precio del monopolio (Romer, 1990, p. 87):
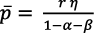 (5)
(5)
El beneficio monopólico es (Romer, 1990, p. 87):
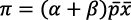 (6)
(6)
La ecuación (6) puede ser deducida de las ecuaciones (4) y (5).
El costo hundido de la inversión en un nuevo diseño, PA, es el valor presente de un flujo infinito de beneficios, descontado con la tasa de interés r(t) (Romer, 1990, p. 87):
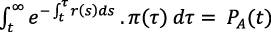 (7)
(7)
Si PA fuera constante resulta (Romer, 1990, p.87):
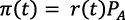 (7 bis)
(7 bis)
El PA de los i = A diseños es igual para todos porque existe libre entrada en el mercado de diseños (Romer, 1990, p. 73).
Según la ecuación (8) el acervo agregado de diseños crece exponencialmente (Romer, 1990, p. 83):
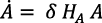 (8)
(8)
δ es un parámetro de productividad
La producción de diseños es lineal en A lo que permite un crecimiento ilimitado (Romer, 1990, p. 84).
El capital humano dedicado a la producción del bien final y el capital humano dedicado a la producción de nuevos diseños tienen la restricción (Romer, 1990, p.85):
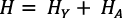 (9)
(9)
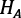 recibe todo el ingreso del sector, el salario del sector es (Romer, 1990, p. 91):
recibe todo el ingreso del sector, el salario del sector es (Romer, 1990, p. 91):
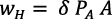 (10)
(10)
La condición de equilibrio para la asignación de H entre Hy y HA es que los salarios en ambos sectores sean iguales. En el producto final el salario de 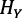 es su producto marginal. En consecuencia es (Romer, 1990, p. 91):
es su producto marginal. En consecuencia es (Romer, 1990, p. 91):
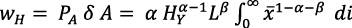 (11)
(11)
Debido a la simetría resulta:
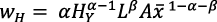 (11 bis)
(11 bis)
Al seguir a Ramsey (1928), las preferencias de los consumidores expresan una relación paralela entre la tasa de crecimiento del consumo y la tasa marginal de sustitución intertemporal. Los consumidores tienen preferencias descontadas de elasticidad de sustitución constante 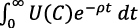 , .
, . 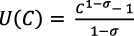 es la función de utilidad;
es la función de utilidad; 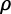 es la tasa de descuento del consumo y
es la tasa de descuento del consumo y 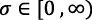 es el coeficiente de aversión al riesgo que determina la sustitución intertemporal del consumo.
es el coeficiente de aversión al riesgo que determina la sustitución intertemporal del consumo.
La condición de optimización intertemporal para un consumidor con tasa de interés fija, r, es (Romer, 1990, p. 88):
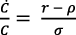 (12) 5
(12) 5
En t = 0, los consumidores son propietarios de las empresas productoras de bienes duraderos y perciben sus beneficios como dividendos (Romer, 1990, p. 88).
Los precios presentes se miden en unidades de producto corriente. Dado que los bienes pueden convertirse en capital “uno por uno”, el precio presente del capital es 1 y su tasa de rendimiento es r (Romer, 1990, p. 85): 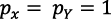 .
.
Solamente la ecuación (4) no está explicitada en Romer (1990), pero su existencia es lógica en su sistema de ecuaciones, porque es la cantidad resultante del problema de maximización del monopolio y está implícita en las ecuaciones (5) y (6).
3. Algunos problemas de este modelo neoclásico
3.1. Consideraciones previas
Romer (1990) no propone ninguna ecuación de comportamiento de r(t); no existe mercado de dinero que determine r(t), ni un Banco Central que la fije políticamente; r(t) es la tasa pagada como costo del capital y retribuida a los propietarios-consumidores por sus ahorros o dividendos (ecuación 12). Pero, como es usual en la teoría neoclásica, r(t) es igual al PMgK y, por lo tanto, es una variable endógena.
El PMgK variable se obtiene a partir de la función de producción (1):
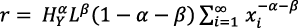 (13)
(13)
Dada la simetría, es:
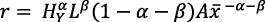 (13 bis)
(13 bis)
Romer (1990), no explicita si la tasa de interés es constante o variable en el problema de maximización del monopolio. Por ello, se estudiará la implicancia de ambas posibilidades.
3.2. Problemas si la tasa de interés iguala al producto marginal del capital al considerarla como dada
En el problema de maximización r(t) parece considerada "como si fuera constante" (Romer, 1990, p. 88). Cada monopolista individual sería demasiado pequeño para afectar la tasa de interés de equilibrio.
Efectivamente, las ecuaciones (5) y (6) son obtenidas de la ecuación (4), que requiere r constante en el problema de maximización. Pero de la ecuación (4) se obtiene:
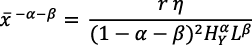
Al substituir esta expresión en la ecuación (13 bis) resulta:
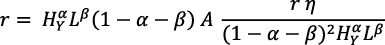
Al simplificar, resulta: 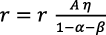
Esto exige r = 0 o bien 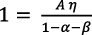 . En la ecuación (4), r = 0 es imposible; en la ecuación (12), si es r = 0 la tasa de crecimiento del consumo sería negativa. Al aceptar la segunda posibilidad:
. En la ecuación (4), r = 0 es imposible; en la ecuación (12), si es r = 0 la tasa de crecimiento del consumo sería negativa. Al aceptar la segunda posibilidad:
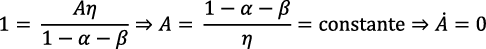
Al considerar r “como si fuera constante” en el problema de maximización, en Romer (1990) no habría cambio tecnológico endógeno. La senda del crecimiento equilibrado sería un estado estacionario.
3.3. Problemas si la tasa de interés es igual al producto marginal del capital al considerarla como variable
El crecimiento equilibrado requiere que A crezca a una tasa exponencial constante y el equilibrio es analizado a través de una cadena de supuestos condicionados que dependen de que r esté "fija" (Romer, 1990). Si esas condiciones se verifican, el equilibrio de largo plazo existirá con un valor de r que sería “fijo”, pero endógeno.
En tal caso, las tasas de crecimiento de todas las variables resultarían:
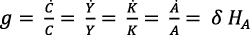 (14)
(14)
Dadas las ecuaciones (14) y (12), resulta (Romer, 1990, p. 92):
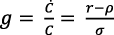 (15)
(15)
Romer (1991) dice:
Dada la forma supuesta de las preferencias, un nivel fijo de A conducirá a un equilibrio con un estado estable en el cual el nivel de K se determina por el requerimiento de que el producto marginal del capital sea igual a la tasa de descuento. (1991, p. 464)
Aquí Romer (1990) acepta que es PMgK = r, como en Ramsey (1928). Pero ese estado “estable” no depende de un nivel de A arbitrariamente fijado, sino que sería la consecuencia del valor endógeno de r como PMgK.
De hecho, puesto que r depende de x, se debe substituir r, según la ecuación (13 bis), en el problema de maximización:
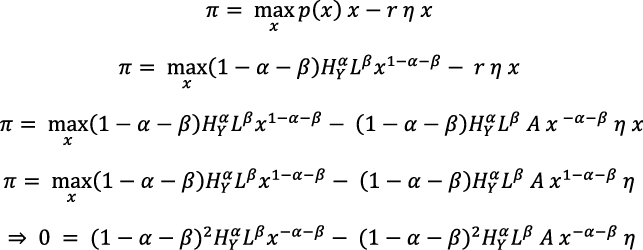
Al pasar de miembro el término negativo y simplificar, resulta:
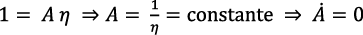 (16)
(16)
Alternativamente, se puede considerar la ecuación (7) de Romer (1990, p. 89), para hallar el PMgK:
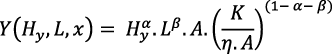
Diferenciando con respecto a K resulta:
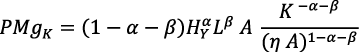
Al multiplicar y dividir por K es:
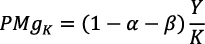
Al reemplazar según la ecuación (3 bis) y luego al simplificar resulta:
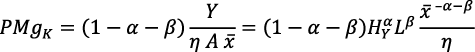
Pero PMgk = r, por lo tanto, al igualar esta ecuación y la ecuación (13 bis), resulta:
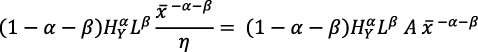
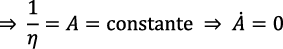
Para un valor de r = PMgK, el modelo de Romer (1990), implica un nivel de A constante, lo que significa que no existe cambio tecnológico endógeno.
Esto es cierto para cualquier valor de x. En efecto, se puede manipular el problema de maximización de otra forma:
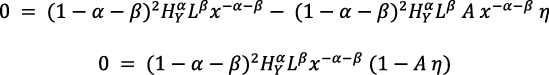
Esto solo puede ser verdadero si 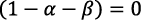 , si
, si 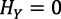 , si
, si 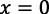 , o si
, o si 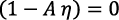 ;
; 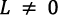 por hipótesis.
por hipótesis.
Pero si 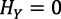 o si
o si 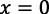 , el producto final en la ecuación (1) sería Y = 0.
, el producto final en la ecuación (1) sería Y = 0.
Además, 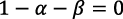 es inconsistente con la ecuación (1).
es inconsistente con la ecuación (1).
Al ser A un conteo del número de diseños de x(i), si fuera x(i) = 0 para todo i, entonces sería también A = 0.
En consecuencia, debe ser:
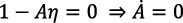
La ecuación (4) no puede ser una solución al problema de maximización si el costo del capital r es el valor endógeno del PMgK. No se puede obtener ninguna expresión formal válida para un valor de equilibrio de x, porque de
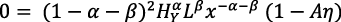
sólo se puede obtener la expresión imposible:
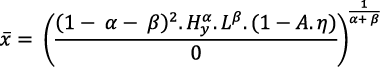
Dado que 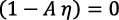 esta expresión es la indeterminación
esta expresión es la indeterminación 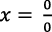 .
.
Existen infinitas soluciones simultáneas para 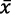 y para todas es
y para todas es 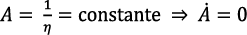 .
.
Para cada una de las infinitas soluciones simultáneas, al tener presentes las ecuaciones (16), (8) y (15), es:
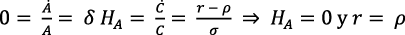 (17)
(17)
Si 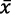 está indeterminado, muchas otras ecuaciones de Romer (1990) lo estarán también, así como el conjunto del modelo.
está indeterminado, muchas otras ecuaciones de Romer (1990) lo estarán también, así como el conjunto del modelo.
Dada la necesaria igualdad de las tasas de crecimiento para un equilibrio dinámico, todas ellas serían iguales a 0 en la ecuación (14). Este curioso resultado es coherente con la teoría de Fisher (1907), sobre la tasa de interés y la preferencia sobre el tiempo, o con su teoría sobre la impaciencia humana, Fisher (1930), que significa la igualdad 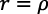 , habitualmente aceptada en la economía neoclásica (Varian, 1992, pp. 426-429).
, habitualmente aceptada en la economía neoclásica (Varian, 1992, pp. 426-429).
Las relaciones de Romer (1990) permiten, no obstante, imaginar una interpretación económica a este resultado indeterminado.
De la ecuación (Romer, 1990, p. 91):
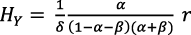 (18)
(18)
y de la constante definida por los parámetros tecnológicos (Romer, 1990, p. 92):
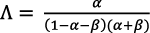 (19)
(19)
Al substituir (19) en (18) e igualar r con 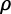 resultaría:
resultaría:
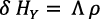 (20)
(20)
Por lo tanto, la tasa del hipotético crecimiento equilibrado del modelo en términos de los parámetros (Romer, 1990, p. 92), dadas las ecuaciones (20), (15) y (17), resultaría:
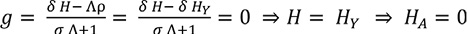 (21)
(21)
Con abuso de la interpretación económica de un modelo indeterminado, podría decirse que si la tasa de descuento del consumo es igual a la tasa que retribuye el ahorro de los consumidores-propietarios, estos no tendrían incentivos para invertir en nuevos diseños; todo el acervo de H sería dedicado a 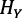 y no habría cambio tecnológico.
y no habría cambio tecnológico.
3.4. Problemas con el valor del producto marginal del capital (VPMgK)
El reverso de la ingeniería, ecuación (13 bis), es la suma de todas las funciones de demanda inversa de cada producto intermedio e implícitamente dice que p(i) es el Valor del Producto Marginal; p(i) es la productividad marginal del iésimo bien de capital que, a su vez, es la curva de demanda inversa del iésimo productor de bienes intermedios.
El precio p(i) de los bienes de capital es su VPMgK, pero como el precio de x(i) es 1, resulta p(i) = r. Esto es consecuencia del supuesto de que los bienes de capital se producen en un sector que tiene la misma tecnología que el sector del producto final (Romer, 1990, p. 80).
Como se ha visto: 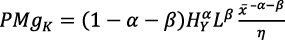
El VPMgK es el precio de equilibrio de p(i): 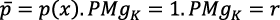
Y esto es: 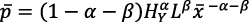
En consecuencia, debe ser 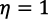 .
.
Pero si r = PMgK, con r variable en el problema de maximización, resulta 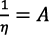 . En tal caso, las cantidades de diseños patentados, de bienes de capital en producción y de empresas monopolistas es A = 1, lo que significa que no hay cambio tecnológico endógeno.
. En tal caso, las cantidades de diseños patentados, de bienes de capital en producción y de empresas monopolistas es A = 1, lo que significa que no hay cambio tecnológico endógeno.
Además, con 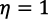 , en la ecuación (5) resulta:
, en la ecuación (5) resulta: 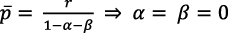 , lo que contradice la ecuación (1).
, lo que contradice la ecuación (1).
Asimismo, resulta: 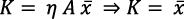
3.5. Problemas con la identidad entre la tasa de crecimiento equilibrado y la condición de optimización intertemporal de Ramsey (1928)
A diferencia de Romer (1990), en Ramsey (1928) la tasa de crecimiento g, a la cual crece A, es exógena y no tiene que ser necesariamente igual a la tasa de crecimiento del consumo de la ecuación (12).
Según la ecuación (15): 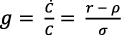 . Esta igualdad acarrea serias consecuencias para el modelo de Romer (1990).
. Esta igualdad acarrea serias consecuencias para el modelo de Romer (1990).
En Ramsey (1928) son posibles 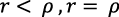 y
y  6 ya que r no es una constante.
6 ya que r no es una constante.
Con respecto a 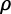 , cabe considerar las afirmaciones de Laibson (1997a, 1997b) y Ramsey (1928) citados por Barro & Sala-i-Martín (2009), quienes dicen:
, cabe considerar las afirmaciones de Laibson (1997a, 1997b) y Ramsey (1928) citados por Barro & Sala-i-Martín (2009), quienes dicen:
La mayor parte de los modelos macroeconómicos básicos … se basa en el supuesto de que los hogares tienen una tasa de preferencia 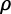 constante. Sin embargo, la base lógica de este supuesto no está clara. (…) [Ramsey] prefiere utilizar una tasa de preferencia temporal igual a cero. (…) [Por otra parte se] ha hecho observaciones muy convincentes en lo que respecta a la manera en que varían las tasas de preferencia temporal. (pp. 121-122)
constante. Sin embargo, la base lógica de este supuesto no está clara. (…) [Ramsey] prefiere utilizar una tasa de preferencia temporal igual a cero. (…) [Por otra parte se] ha hecho observaciones muy convincentes en lo que respecta a la manera en que varían las tasas de preferencia temporal. (pp. 121-122)
Es legítimo analizar las consecuencias de una interferencia exógena en las expectativas de los consumidores que altere sus preferencias sobre el futuro, al modificar las relaciones entre r y 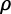 .
.
Si 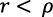 la condición de optimización dinámica es
la condición de optimización dinámica es 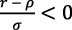 y la tasa de crecimiento del consumo sería negativa. Con
y la tasa de crecimiento del consumo sería negativa. Con 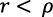 y dada la ecuación (17), la igualdad de las tasas de crecimiento en el equilibrio endógeno del modelo es un absurdo:
y dada la ecuación (17), la igualdad de las tasas de crecimiento en el equilibrio endógeno del modelo es un absurdo:
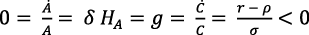 (22)
(22)
La tasa de cambio tecnológico endógeno no puede ser nula ni negativa (A es el número creciente de diseños de bienes de capital indestructibles).
Un problema similar resulta con  .
.
Esto significa que con 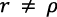 no existe crecimiento equilibrado y con
no existe crecimiento equilibrado y con 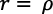 , el “crecimiento” equilibrado es un estado estacionario sin cambio tecnológico endógeno.
, el “crecimiento” equilibrado es un estado estacionario sin cambio tecnológico endógeno.
4. Una formalización más allá del modelo neoclásico
Dado que la más importante consecuencia es que el PMgK no puede ser igual a r, se abandonará este supuesto neoclásico habitual. Se introduce el dinero fiduciario y la política monetaria; r(t) será una variable distributiva exógena.
Ahora existe un grado de libertad con r(t) como variable libre. Este concepto teórico no neoclásico guarda semejanza con Sraffa (1960).
Se supondrá que existe una autoridad monetaria que administra políticamente una tasa de interés de mercado en función de la estabilidad de precios para el crecimiento equilibrado; la liquidez sería gestionada al estilo de una “regla de Taylor” (Taylor, 1993).
Se supondrá también que los consumidores-ahorradores no son las mismas personas que los propietarios del capital. Los consumidores ahorran su dinero en los bancos y su retribución es r(t); las empresas toman préstamos en dinero de los bancos y su costo es r(t). Por simplicidad, se considera iguales esas dos tasas.
Se abandonará el supuesto neoclásico habitual de 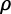 como parámetro fijo. Siguiendo a Laibson 1997a, 1997b citados por Barro & Sala-i-Martín (2009), estos autores dicen:
como parámetro fijo. Siguiendo a Laibson 1997a, 1997b citados por Barro & Sala-i-Martín (2009), estos autores dicen:
Teniendo en cuenta estos puntos de vista y los datos empíricos [sobre las variaciones de las tasas de preferencia temporal], es importante plantear si los economistas podemos seguir dependiendo de la versión estándar del modelo neoclásico de crecimiento … como el modelo básico de la macroeconomía dinámica. (p. 122)
Se definirá 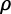 como una variable exógena que depende de las expectativas sobre el futuro; éstas, a su vez, dependen de la estructura institucional y la estabilidad política, exógenas a la estructura económica. Si S es la desviación estándar de las expectativas sobre el futuro como expresión de incertidumbre, es:
como una variable exógena que depende de las expectativas sobre el futuro; éstas, a su vez, dependen de la estructura institucional y la estabilidad política, exógenas a la estructura económica. Si S es la desviación estándar de las expectativas sobre el futuro como expresión de incertidumbre, es:
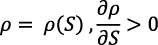
Ahora r(t) no tiene porqué ser igual ni al PMgK ni a ρ(S).
La ecuación (4) es válida, pero con r como variable exógena.
El PMgK se obtiene al derivar con respecto a x la ecuación (1 bis):
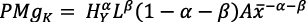 (23)
(23)
Al substituir la ecuación (4) en la (23) y al simplificar resulta:
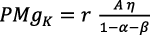 (24)
(24)
La ecuación (24) significa que 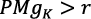 si
si 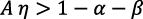 .
.
De la ecuación (24) resulta:
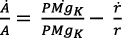 ,
, 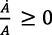 (25)
(25)
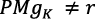 es incompatible con algunos supuestos y resultados de Romer (1990).
es incompatible con algunos supuestos y resultados de Romer (1990).
En efecto, en Romer (1990, pp. 90-91) 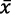 permanece constante en el tiempo. Pero de la ecuación (4) se obtiene:
permanece constante en el tiempo. Pero de la ecuación (4) se obtiene:
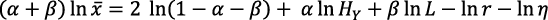
Si 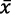 fuera constante, al derivar resulta:
fuera constante, al derivar resulta:
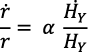
Pero, de la ecuación (18), con 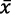 constante, resulta:
constante, resulta:
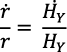
Si fuera 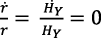 no habría problemas. Pero r no es una constante;
no habría problemas. Pero r no es una constante; 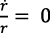 es posible pero no necesaria.
es posible pero no necesaria.
Si fuera 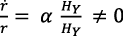 y si se aceptara la ecuación (10) de Romer (1990, p. 91), (ecuación (18) en este trabajo), debería ser
y si se aceptara la ecuación (10) de Romer (1990, p. 91), (ecuación (18) en este trabajo), debería ser 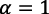 , que contradice la ecuación (1).
, que contradice la ecuación (1).
En consecuencia, 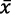 no es constante en el tiempo en la ecuación (4).
no es constante en el tiempo en la ecuación (4).
Al substituir la ecuación (4) en la (1 bis) se obtiene:
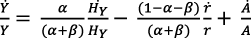 (26)
(26)
Al substituir la ecuación (4) en la (3 bis), se obtiene:
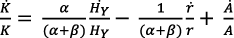 (27)
(27)
Si HA ≠ 0, las tasas para un crecimiento equilibrado serían:
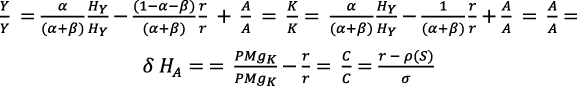 (28)
(28)
Este crecimiento equilibrado es posible solamente si r > ρ. Además, r debe estar fija, 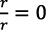 , y por lo tanto
, y por lo tanto 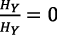 ; en caso contrario, de la igualdad de las ecuaciones (26) y (27) resultaría
; en caso contrario, de la igualdad de las ecuaciones (26) y (27) resultaría 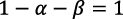 , lo cual contradice la ecuación (1).
, lo cual contradice la ecuación (1).
Así, la ecuación (26) debe ser 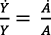 y la ecuación (27) debe ser
y la ecuación (27) debe ser 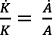
Entonces resulta: 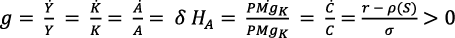 (28 bis)
(28 bis)
Las tasas de crecimiento del PMgK y del consumo deben ser positivas e iguales, pero con el tipo de interés r fijo. Al ser positivo el crecimiento del PMgK al mismo tiempo que la tasa de crecimiento del tipo de interés es 0, con el paso del tiempo, el PMgK, que crece, será cada vez más grande que r, que no crece.
Al considerar el PMgK como el dividendo ganado por los propietarios del capital y r como retribución por los ahorros y costo del capital, la ecuación (28 bis) muestra que el tipo de interés r es diferente y cada vez menor que el dividendo PMgK.
Esto será causa de creciente apalancamiento, al incrementar los beneficios del capital invertido en comparación a los intereses del ahorro prestado. Al asumir que los consumidores-ahorradores son personas diferentes de los propietarios del capital, la desigualdad social será creciente.
5. Política monetaria y cambio tecnológico endógeno
Las relaciones (28 bis) dependen de las expectativas de los consumidores que determinan ρ(S) para r(t) fija. c
Si r = ρ, será 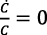 , pero esto no implica que las otras tasas de crecimiento sean 0.
, pero esto no implica que las otras tasas de crecimiento sean 0.
Si 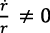 , entonces:
, entonces: 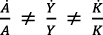 , según las ecuaciones (25), (26) y (27).
, según las ecuaciones (25), (26) y (27).
Una política monetaria activa sería inconsistente con el crecimiento equilibrado porque r debe permanecer fija y mayor que 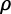 ; pero gestionar políticamente r(t) podría ser útil para aproximar la economía hacia el equilibrio.
; pero gestionar políticamente r(t) podría ser útil para aproximar la economía hacia el equilibrio.
Las variaciones de r(t) afectan la asignación de H entre la producción de nuevos diseños y la producción de bienes de consumo.
En efecto, al substituir la ecuación (4) en la (11) y al igualar con la ecuación (10), tras algunas manipulaciones, se obtiene:
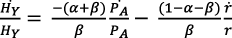 (29)
(29)
Al calcular el valor actual de PA con la ecuación (7 bis) es:
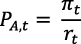
Al aplicar logaritmos y derivar con respecto a r(t) se obtiene:
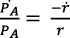 (30)
(30)
Al substituir la ecuación (30) en la (29) se obtiene:
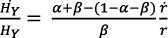 (31)
(31)
Si la elasticidad del producto final Y con respecto al capital x en la ecuación (1 bis) fuera 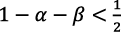 , entonces en la ecuación (31)
, entonces en la ecuación (31) 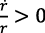 implicaría
implicaría 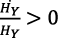 . Se supondrá que este es el caso7.
. Se supondrá que este es el caso7.
Si es 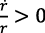 se incrementará
se incrementará 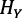 ; entonces, dadas las ecuaciones (8) y (9), se reducirá
; entonces, dadas las ecuaciones (8) y (9), se reducirá 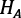 y la tasa de crecimiento de la tecnología será más baja.
y la tasa de crecimiento de la tecnología será más baja.
Según la ecuación (25), al aumentar hasta cierto nivel  , podría ser
, podría ser 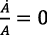 ; pero simultáneamente el aumento de r incrementaría
; pero simultáneamente el aumento de r incrementaría  , según la ecuación (12).
, según la ecuación (12).
Si es 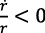 el efecto sería simétrico.
el efecto sería simétrico.
Las variaciones de r(t) también afectan el beneficio de los monopolistas.
Si es 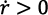 ,
, 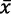 tendría un menor valor según la ecuación (4) y un p(x) más alto, según la (5). El monopolista trabaja con una elasticidad-precio de la demanda mayor que 1 y, en consecuencia, el crecimiento de r(t) disminuye sus ingresos. Además, incrementar r(t) aumenta los costos. Esto implica una reducción del beneficio, como se puede ver en la ecuación (6).
tendría un menor valor según la ecuación (4) y un p(x) más alto, según la (5). El monopolista trabaja con una elasticidad-precio de la demanda mayor que 1 y, en consecuencia, el crecimiento de r(t) disminuye sus ingresos. Además, incrementar r(t) aumenta los costos. Esto implica una reducción del beneficio, como se puede ver en la ecuación (6).
Si una economía crece según la ecuación (28 bis), la política monetaria podría estar interesada en mantener r(t) constante. Aunque debe tenerse en cuenta que este crecimiento es “equilibrado” solo en algunas de las variables del sistema. En efecto, simultáneamente están creciendo el apalancamiento financiero de las empresas y la desigualdad social, lo que significa un desequilibrio en otras variables del sistema.
En dicha situación, la tasa de crecimiento del consumo puede ser modificada por un choque exógeno en las expectativas que incremente 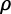 (S); esto interrumpirá la igualdad de las tasas de crecimiento en la ecuación (28 bis) y no existirá un retorno endógeno automático a dicho equilibrio, porque
(S); esto interrumpirá la igualdad de las tasas de crecimiento en la ecuación (28 bis) y no existirá un retorno endógeno automático a dicho equilibrio, porque 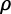 (S) y r(t) son variables exógenas.
(S) y r(t) son variables exógenas.
Si sucede esto, la política monetaria puede aproximar la economía hacia una nueva senda de crecimiento al gestionar r(t) entre dos restricciones.
Por un lado, dadas lasecuaciones (12) y (24), debería ser:
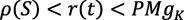
En segundo lugar, según la ecuación (25), debería ser:
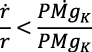
Conducir la economía hacia un nuevo equilibrio según la ecuación (28 bis), después de un choque en las expectativas que incremente 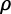 (S), puede ser muy dificultoso si el PMgK es muy bajo en comparación con
(S), puede ser muy dificultoso si el PMgK es muy bajo en comparación con 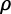 (S) o si el PMgK está creciendo a una tasa muy baja que obligue a una de variación de r(t) incompatible con la dinámica de crecimiento del consumo.
(S) o si el PMgK está creciendo a una tasa muy baja que obligue a una de variación de r(t) incompatible con la dinámica de crecimiento del consumo.
6. Globalización financiera y crecimiento nacional endógeno
En una economía abierta resulta inconsistente la coexistencia de: a) libre circulación de capitales, b) soberanía monetaria y c) tipo de cambio fijo.
En la globalización financiera rige la libre circulación de capitales; entonces, cada economía sólo puede optar entre la soberanía monetaria (con capacidad de fijar su tasa de interés) y establecer el tipo de cambio de su moneda con las demás divisas.
Se introduce un concepto teórico no neoclásico: el dinero pasivo internacional y la hegemonía monetaria (Olivera, 1982).
Cuando el Sistema Monetario Internacional (SMI) con libre circulación de capitales, además de las divisas de todos los países, posee como “dinero internacional” activos no emitidos por ningún país, el sistema posee un grado de libertad. El equilibrio exige definir exógenamente una variable. La economía que puede hacerlo adquiere la hegemonía monetaria y es la única que puede definir políticamente su oferta de dinero y su tipo de cambio. Los demás países deben elegir si prefieren fijar su oferta monetaria o su tipo de cambio.
Si en dicho SMI existe la necesidad, para las economías pequeñas, de priorizar la estabilidad del tipo de cambio, (si establecen cajas de conversión o adoptan una moneda no nacional como dinero doméstico), se resigna la soberanía monetaria y la determinación de su tasa de interés.
En este contexto, “el arbitraje concerniente a los tipos de interés, … conduce a un tipo de interés único en el mundo” (Jetin, 2005, p. 42).
La tasa de interés internacional, r*, gestionada por la autoridad monetaria hegemónica, es exógena para los bancos centrales no hegemónicos.
Aunque r* sea internacional y exógena, las expectativas de los consumidores, el producto marginal del capital y el progreso tecnológico nacional continúan siendo domésticos y endógenos.
En los PMDs la incertidumbre y los riesgos a futuro suelen ser mayores que en los PIs; se supone entonces que: 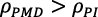 .
.
En los PIs r* puede alcanzar un valor muy bajo coherente con 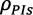 . Esto podría generar:
. Esto podría generar: 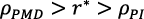 .
.
Los fondos financieros, el capital humano y las infraestructuras disponibles para la investigación tecnológica, suelen ser menores en los PMDs que en los PIs; en consecuencia:
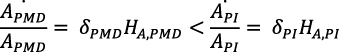
Si las economías en los PIs crecen según la ecuación (28 bis), con una tasa de interés global r* muy baja, fijada políticamente, esto podría generar efectos adversos para los PMDs.
En los PIs podría cumplirse la ecuación (28 bis):
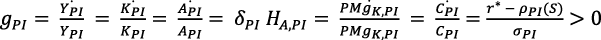 (32)
(32)
Pero r* muy baja desequilibraría el crecimiento en algunos PMDs, cuya situación doméstica y en comparación con los PIs podría ser:
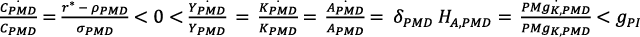 (33)
(33)
En este modelo, la palabra "consumo" significa "consumo de Y", es decir, de la producción nacional de bienes finales. Si el desequilibrio de la ecuación (33) se sostiene el tiempo suficiente, la tasa de crecimiento del producto final en los PMDs será negativa y el desempleo crecerá permanentemente.
Si el producto final de algunos PMDs no es competitivo internacionalmente, sus economías reemplazarán bienes finales nacionales, YPMD, por importados, YPI . Finalmente, una porción de su desempleo emigrará hacia los PIs, cuyo crecimiento según la ecuación (32) demanda más trabajo.
La desigualdad social se incrementará en los PMDs: el dividendo del capital invertido, PMgK,PMD, crece en la ecuación (33) a una tasa positiva con r* fija en su valor muy bajo, mientras la tasa de crecimiento del consumo es negativa con desempleo creciente.
Además, con una r* muy baja y un ahorro interno decreciente por el desempleo, el apalancamiento empresarial financiará, con créditos externos, una producción no transable y desequilibrará la balanza de pagos.
En las condiciones estructurales de este modelo teórico, las sendas de crecimiento de los PMDs y de los PIs no se ajustarían a la teoría de la convergencia, sino que serían divergentes.8
7. Algunos hechos estilizados de la dinámica global en las últimas décadas
Se asume las siguientes definiciones:
I) Hechos estilizados de la dinámica del crecimiento de algunos PIs:
• revolución tecnológica endógena
• tasa de interés muy baja durante un tiempo prolongado
• alto apalancamiento empresarial que creó burbujas financieras
• inmigración masiva procedente de los PMDs
• aumento de las desigualdades sociales por la deslocalización de empresas, la reducción de costos laborales y la inmigración
• crisis por la explosión de la burbuja financiera/inmobiliaria
• limitado impacto en la recuperación de la subsiguiente política monetaria expansiva
• crecimiento desequilibrado, con crisis financieras, excesos de endeudamiento público, riesgos de default y ajustes fiscales.
Una interpretación plausible:
• tras la expansión de la revolución tecnológica, la crisis por la explosión de la burbuja financiera restringe el crédito y el apalancamiento y frena la inversión;
• los propietarios del capital no son las mismas personas que los consumidores-ahorradores;
• cuando las expectativas pesimistas de los consumidores-ahorradores elevan 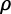 (S), la reducción de r(t) para estimular la inversión puede implicar
(S), la reducción de r(t) para estimular la inversión puede implicar 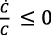 y que los consumidores-ahorradores no tengan incentivos para ahorrar;
y que los consumidores-ahorradores no tengan incentivos para ahorrar;
•no existe un mecanismo de retorno automático a la senda de crecimiento equilibrado.
II) Hechos estilizados de la dinámica del crecimiento de algunos PMDs:
• abandono de la soberanía monetaria con r* en el mercado doméstico
• control del tipo de cambio como opción en la “trinidad imposible”; tendencia a tipos de cambio fijos con adopción de cajas de conversión o de una divisa extranjera como moneda doméstica
• crecimiento económico modesto pese a r* muy baja, con sustitución de producción nacional por consumo importado
• escaso progreso tecnológico
• expulsión de población hacia los PIs
• incremento de sus desigualdades sociales.
Una interpretación plausible:
• cada economía tiene expectativas de sus consumidores y patrones de innovación tecnológica que son particulares y asimétricos con los PIs;
• los países pierden la capacidad de gestionar r(t) para aproximarse al equilibrio, cuando pierden su soberanía monetaria;
• la diferenciación entre los propietarios del capital y los ahorradores-consumidores es mucho mayor que en los Pis;
• r* muy baja puede generar 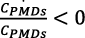 para la producción nacional; esto conduciría a
para la producción nacional; esto conduciría a 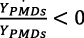 y a un incremento del desempleo;
y a un incremento del desempleo;
• r* muy baja, al estimular la producción y el consumo en los PIs, incrementa la demanda de trabajo allí. El desempleo en los PMDs es atraído por la demanda laboral en los PIs;
• 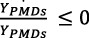 hace que el capital humano sea lo primero en emigrar a los PIs;
hace que el capital humano sea lo primero en emigrar a los PIs;
• el estallido de la burbuja financiera en los PIs agrava la situación al restringir el crédito externo y al afectar las exportaciones de los PMDs hacia los PIs;
• no existe un mecanismo de retorno automático al crecimiento equilibrado; sin soberanía monetaria la política del banco central tampoco existe.
III) Hechos estilizados de la dinámica del crecimiento global:
• globalización financiera con irrestricta movilidad de capitales y multiplicación de activos líquidos internacionales
• aumenta la brecha de renta per cápita entre PIs y PMDs en términos absolutos y en tasa de crecimiento.
• Una interpretación plausible:
• si la tasa de interés internacional es la misma en todos los países, el SMI es un único sistema para todos los países;
• una única tasa de interés global, cuyos efectos pueden ser inversos en economías diferentes dadas las asimetrías, puede ser causa de divergencia en ingreso per cápita.
8. Conclusión
Los hechos resultan mejor interpretados con un modelo teórico en el cual:
a) las economías no retornan endógenamente al crecimiento equilibrado;
b) no existe convergencia automática de renta per cápita entre PIs y PMDs
c) el dinero no es un numerario representable por cualquier bien;
d) la tasa de interés no está determinada por la tecnología de la función de producción;
e) las preferencias no son parámetros constantes;
f) el SMI globalizado no es un mercado perfectamente competitivo.
9. Referencias
Blanchard, O. (2002). Macroeconomía. Madrid: Prentice Hall.
Barro, R. & Sala-i-Martín, X. (2009). Modelos de crecimiento con optimización del consumidor (el modelo de Ramsey). En Reverte (Ed),Crecimiento económico (pp. 85–142). Barcelona, España. Recuperado de https://books.google.es/books?isbn=8429126147
Fisher, I. (1907). The Rate of Interest: Its nature, determination and relation to economic phenomena. New York: The Macmillan Co. Recuperado de https://books.google.es/books?id=zEJZAAAAYAAJ
Fisher, I. (1930). The Theory of Interest As Determined by Impatience to Spend Income and Opportunity to invest it. En A.M. Kelley(Eds), reimpresión del Editor David Rehak). Recuperado de https://books.google.co.cr/books/about/The_theory_of_interest.html?id=4J5FAQAAIAAJ&redir_esc=y
Jetin, B. (2005). Un impuesto contra la especulación con divisas. En La tasa Tobin – Un arma para detener la expoliación financiera (Trad. Griselda Piñero). En Agencia Latinoamericana de Información y Análisis Dos (Eds). La taxe Tobin et la solidarité entre les nations (pp. 19–63). Recuperado de https://livre.fnac.com/a1270301/B-Jetin-La-taxe-Tobin-et-la-solidarite-entre-les-nations
Krugman, P. y Wells, R. (2016). Crecimiento económico a largo plazo. En Reverté (Ed), Macroeconomía(pp. 241–273). Recuperado de https://www.marcialpons.es/autores/krugman-paul-r/1019456/
Maddison, A. (2008). Statistics on World Population, GDP, and Per Capita GDP, 1-2008 AD. En Historical Statistics. University of Groningen. Recuperado de http://www.ggdc.net/maddison/oriindex.htm
Mankiw, N., Romer, D. & Weil, D. (1992). A Contribution to the Empirics of Economic Growth. En The Quarterly Journal of Economics, 2(107), 407 – 437. Doi: https://doi.org/10.2307/2118477
Olivera, J. (1982). Dinero Pasivo Internacional y Hegemonía Monetaria. En Desarrollo económico, Journal Article: Instituto de Desarrollo Económico Y Social. 89(23), 3-9. Doi: https://doi.org/10.2307/3466444
Ramsey, F. (1928). A Mathematical Theory of Saving. En The Economic Journal, Journal Article 152(38), 543 -559. Doi: https://doi.org/10.2307/2224098
Romer, D. (1996). Advanced Macroeconomics. New York: MC Graw-Hill Publishers. Recuperado de https://books.google.es/books?id=2adfDwAAQBAJ
Romer, P. (1990). Endogenous Technological Change. En Journal of Political Economy, 5(98), S71-S102. Doi: https://doi.org/10.1086/261725
Romer, P. (1991). El cambio tecnológico endógeno. El Trimestre Económico, 231(58) ,441-480. Recuperado de https://www.jstor.org/stable/23397462?seq=1#page_scan_tab_contents
Sraffa, P. (1960). Production of commodities by means of commodities: Prelude to a Critique of Economic Theory. Cambridge: The Syndics of Cambridge University Press. https://books.google.es/books?id=SJw8AAAAIAAJ&hl=es&source=gbs_navlinks_s
Taylor, J. (1993). Discretion and Policy Rules in Practice. Carnegie-Rochester Conference Series on Public Policy, (39), 195-214. Doi: https://doi.org/10.1016/0167-2231(93)90009-L
Varian, H. (1992). El tiempo. En Antoni Bosch (Ed), Análisis Microeconómico. (pp. 421–431). Barcelona, España. Recuperado de https://books.google.es/books?isbn=8485855639
1 Este artículo expone las ideas de la ponencia del autor “Monetary Policy, Consumer’s Expectation and Endogeonous Technological Change in a Globalized Economy”, en el XXVII Congreso Internacional de Economía Aplicada, ASEPELT 2013, Zaragoza, julio 2013, publicada en Anales de economía aplicada, ISSN: 2174-3088, DELTA Publicaciones Universitarias, S.L. y ASEPELT, Issue XXVII, 2013.
2 Doctor en Economía con Especialidad en Teoría Económica, Universidad de Barcelona, España. Profesor Colaborador de los Estudios de Economía y Empresa, Universitat Oberta de Catalunya (UOC), España. Correo electrónico: firmenich@economistes.com
3 Todas las citas textuales de este artículo se refieren a la versión castellana publicada en Romer (1991). Las referencias a dicho artículo sin cita textual serán indicadas en el texto con la página de la edición original en inglés de Romer (1990).
4 Para Romer (1990, p. 80) la función de producción (1) está definida como un número discreto de bienes intermedios, aunque la ecuación de salarios (11), derivada de la misma función de producción, está definida como un continuum de bienes intermedios en Romer (1990, p. 91).
5 En la ecuación (12) debe ser 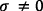 . La restricción usual para este parámetro en Ramsey (1928) es
. La restricción usual para este parámetro en Ramsey (1928) es 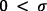 ; debería ser
; debería ser 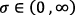 . Véase Romer (1996, pp. 39–40). El error tipográfico se repite en la edición en castellano citada.
. Véase Romer (1996, pp. 39–40). El error tipográfico se repite en la edición en castellano citada.
6 Véase Romer (1996, p. 45): “Thus [la Ecuación de Euler en el modelo de Ramsey, ecuación 12 en este trabajo] states that consumption per worker is rising if the real return exceeds the rate at which the household discounts future consumption, and is falling if the reverse holds”.
(TRADUCCIÓN PROPIA:“Por lo tanto [la Ecuación de Euler en el modelo de Ramsey, ecuación 12 en este trabajo] establece que el consumo por trabajador está creciendo si el rendimiento real es mayor que la tasa a la cual las familias descuentan el consumo futuro y está cayendo si es al revés.”)
7 Las estimaciones empíricas de esta elasticidad realizadas por Mankiw, Romer & Weil (1992) coinciden con este supuesto.
8 La conclusión contraria a la hipótesis de la convergencia es teórica y no empírica. Aunque los hechos estilizados que fundamentan esta conclusión son compatibles con la evidencia empírica; autores como, Romer (1996, pp. 27–31), Blanchard (2002, pp. 198–200) y Krugman & Wells (2016, pp. 262–263) sostienen que dicha hipótesis se verifica entre países ricos, pero no en el conjunto del mundo. Hay evidencia de que la brecha en renta per cápita entre los países industrializados y los países menos desarrollados está aumentando. Para una mayor colección de datos estadísticos, véase Maddison (2008).
 |
 |
 |

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.