Economía y Sociedad, Vol. 20, Nº 48 Cierre al 31 de diciembre de 2015, pp. 1-29 EISSN: 2215-3403 URL http://www.revistas.una.ac.cr/economia

PRONÓSTICOS DE INFLACIÓN MEDIANTE TÉCNICAS BAYESIANAS

INFLATION FORECASTS USING BAYESIAN TECHNIQUES

Juan Diego Chavarría Mejía1

Carlos Chaverri Morales2

Resumen

La efectividad de la política monetaria bajo un esquema de metas de inflación como el propuesto por el Banco Central de Costa Rica se basa en buena medida en el correcto y oportuno pronóstico de la inflación a corto y mediano plazo con el fin de diseñar de mejor forma las acciones de política monetaria. Así, el propósito de este trabajo es desarrollar una herramienta complementaria para elaborar pronósticos de inflación mediante un enfoque bayesiano. Para lo anterior se propone la utilización de la metodología Bayesian Model Averaging y de Weighted Average Least Squares. Los modelos de proyección especificados permitirían ampliar y complementar el análisis que se realiza actualmente con el Modelo Macroeconómico de Proyección Trimestral (MMPT) del Banco Central de Costa Rica. Como resultado esta investigación muestra que, para datos de periodicidad mensual y a horizontes de pronóstico de 1 a 12 meses, es posible encontrar proyecciones mediante un proceso bayesiano que poseen una mayor capacidad predictiva en relación con aquellas producidas por un modelo autorregresivo.

Palabras clave: Modelos de series temporales; números índice y agregación; predicción y simulación; análisis bayesiano.

Abstract

The effective monetary policy using the inflation targeting scheme proposed by the Central Bank of Costa Rica is mostly based on the correct and timely inflation forecast in the short and medium term, in order to better design monetary policy actions. The purpose of this study is to develop a complementary tool to forecast inflation using a Bayesian approach. To that end, we propose using the Bayesian Model Averaging and Weighted-Average Least Squares methodologies. Such projection models allow expanding and complementing the analysis currently conducted by the Central Bank of Costa Rica using the Quarterly Macroeconomic Projection Model (MQPM). As a result, we show that for monthly data and forecasting 1 to 12 months in advance, it is possible to have projections using the Bayesian process with greater predictive performance than with the autoregressive model.

Keywords: time-series models; index numbers and aggregation; forecasting and simulation; bayesian analysis.

Doi: http://dx.doi.org/10.15359/eys.20-48.3

Fecha de recepción: 27-05-15 Fechas de reenvíos: 14-09-15/20-10-15.

Fecha de aceptación: 26-10-2015. Fecha de publicación: 02-11-15

Introducción

La política monetaria en Costa Rica se encuentra en un proceso de ajuste ante la migración gradual de un régimen monetario basado en el control de los agregados monetarios hacia un sistema de Meta Explícita de Inflación3. Es reconocido en la literatura sobre el tema que en este tipo de régimen, la efectividad de la política monetaria se puede cuantificar, entre otras cosas, en donde se contrasta la evolución de la inflación observada a corto y mediano plazo con la meta anunciada.

De manera prospectiva y haciendo uso de herramientas cuantitativas, dicha evaluación es posible mediante la construcción de pronósticos de inflación. Adicionalmente, la elaboración de indicadores que aíslan la volatilidad, que ciertos precios registran, complementa la información sobre la cual las autoridades toman las decisiones sobre la política monetaria.

En línea con lo anterior y con el fin de ampliar la gama de instrumentos con que cuenta el Banco Central de Costa Rica (BCCR), el Departamento de Investigación Económica ha desarrollado investigación tendiente a elaborar una serie de modelos que le permiten contar con pronósticos de la inflación. La construcción de dichos modelos ha seguido principalmente dos líneas de investigación: i) especificaciones univariadas de series de tiempo y ii) construcción de modelos semiestructurales.

En lo que corresponde a las especificaciones univariadas, se han propuesto modelos autoregresivos con media móvil (ARMA); entre ellos se encuentran los trabajos de Hoffmaister et al. (2000), Muñoz (2008), Rodríguez (2009) y Vindas (2011). En relación con la segunda línea de trabajo, se cuenta con distintos modelos entre ellos: Modelo Univariable de Inflación, Modelo de Vector Autorregresivo Lineal de Mecanismos de Transmisión de la Política Monetaria, Modelo Impacto de los Precios del Petróleo en Costa Rica, Modelo de Títulos Fiscales, Modelo de Pass Through del Tipo de Cambio en Costa Rica y proyecciones basadas en un modelo “ingenuo”4.

Adicionalmente, Álvarez y Torres (2011) estimaron modelos de proyección de inflación a corto plazo que se basa en una especificación de Curva de Phillips para las series trimestrales y mensuales de inflación general (derivada del Índice de Precios al consumidor, IPC) y sus desagregaciones en bienes y servicios transables y no transables.

El presente trabajo tiene como objetivo desarrollar herramientas complementarias para elaborar pronósticos de inflación a partir de la teoría bayesiana. Para lo anterior se propone utilizar la metodología Bayesian Model Averaging (BMA, por sus siglas en inglés) y Weighted Average Least Squares (WALS, por sus siglas en inglés).

Luego de esta introducción, en la segunda sección se presenta una breve reseña de la metodología empleada. En la tercera sección se explicará los criterios para seleccionar las variables que componen la base de datos y el indicador de inflación de referencia. En la cuarta se mencionan los principales resultados. Finalmente, la quinta sección contiene las principales conclusiones de la investigación y las recomendaciones del caso.

Metodología

Un problema que hasta el momento ha sido poco abordado en la literatura y al cual todos los investigadores se enfrentan a la hora de realizar cualquier estudio empírico, es el referente a la incertidumbre5. Este problema surge en el momento de seleccionar una especificación que se considera apropiada para predecir una variable de interés (Steel, 2014). Dentro de las posibles soluciones sobresalen los métodos que aprovechan al máximo toda la información disponible, como pueden ser los modelos basados en métodos bayesianos y de factores dinámicos.

Además del problema sobre cuál es la especificación correcta, existe otro relacionado con las variables que deben ser incluidas. Precisamente, en los años recientes esta dificultad ha tomado cierta relevancia dado el aumento en la cantidad de información a disposición de los investigadores, lo que hace cada vez más difícil determinar qué variables utilizar incluso si se respetan los criterios teóricos que respaldan la validación empírica.

Los modelos para generar pronósticos de inflación no son ajenos a dichos problemas. Por lo tanto, para solucionar las dificultades en este trabajo se propone la utilización de dos métodos bayesianos, con los cuales se busca primordialmente reducir la incertidumbre sobre la especificación del modelo. El primero de ellos es llamado Bayesian Model Averaging, que es un método usual para la generación de pronósticos cuando existe incertidumbre sobre la correcta especificación por utilizar, descrita por Magnus et al. (2010). Mientras el segundo método de estimación que se utiliza es el propuesto por Magnus y Durbin (1999) y Danilov y Magnus (2004) llamado Weighted Average Least Squares.

En ambos enfoques metodológicos la preocupación no se centra en la elección óptima de un modelo, sino buscan las mejores estimaciones de todos los n modelos posibles, para luego ponderar estos resultados mediante su respectiva probabilidad condicional a los datos muestrales.

Por otro lado, con el objetivo de utilizar la mayor cantidad de información disponible, el ejercicio de estimación propone utilizar el enfoque de factores dinámicos. Esta técnica se basa en el uso de las componentes principales como variables sintéticas. El cual es un método de reducción de información donde se intenta maximizar la variabilidad explicada por las variables sintéticas que reducen la distancia entre las observaciones originales y los puntos proyectados sobre estas variables.

Así, con esta técnica se facilita el manejo de una gran cantidad de información contenida en un número reducido de variables, lo cual disminuye la incertidumbre sobre cuáles variables incorporar en las estimaciones definitivas, y adicionalmente, se logra simplificar los requerimientos computacionales para realizar las estimaciones.

La estimación del pronóstico de inflación parte del siguiente modelo lineal normal:

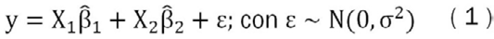
Donde es un vector de n x 1 de observaciones de la variable de interés. Además, se consideran dos conjuntos de variables, el primero representado en la matriz X1 de tamaño n x k1 llamado variables focus6, constituido por las variables sobre las cuales se tiene certeza que deben estar en el modelo7, ya sea por aspectos teóricos o por algún interés empírico particular del investigador.

Adicionalmente, se tiene otro grupo de variables sobre las que no se tiene certeza si deben tomarse en consideración dentro de la especificación, llamadas variables auxiliares. Este grupo se representa en la matriz X2 de tamaño n x k2.

Por último, β1 representa al vector de parámetros de tamaño k1 x 1 de las variables focus y β2 es el vector de parámetros de tamaño k2 x 1 de las variables auxiliares.

Así, del análisis previo resulta relevante preguntarse, ¿cuáles variables auxiliares son convenientes para utilizar? En la literatura sobre el tema no existe una regla definida para dar respuesta a dicha interrogante. Una alternativa intuitiva es probar con diferentes modelos que tomen en cuenta todas las posibles combinaciones de estas variables auxiliares. Donde para cada variable auxiliar se tienen dos modelos posibles, uno llamado modelo restrictivo donde se supone que el coeficiente correspondiente a la variable auxiliar es cero y otro sin restricción donde no se hace dicho supuesto. Si se repite el proceso para todas las k2 variables auxiliares, se tendrán un total de 2k2 modelos posibles, donde a cada uno de estos modelos se podrá llamar como Mi, i = 1, 2, ..., 2k2 . Y se representa:

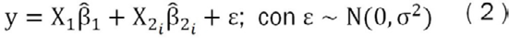
Ahora, para estimar los parámetros de cada modelo (β̂1 y β̂2_i) , se plantean los dos métodos siguientes.

Bayesian model averaging

El primero de ellos es un método propuesto por Magnus et al. (2010), el cual parte de las siguientes regresiones particionadas utilizadas para estimar los parámetros sin restricción de cada modelo:

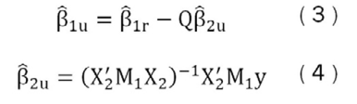
Donde:

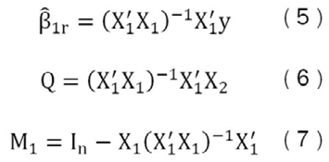
La variable β̂1r representa el vector de parámetros (modelo restringido) de tamaño k1 x 1 de una regresión, en donde se usa el criterio de mínimos cuadrados ordinarios (MCO) explicada solo por las variables consideradas focus. Además, Q es el vector de parámetros de k1 x 1 de una regresión MCO de X2 explicada por las variables focus; y M1 es una matriz de tamaño n x n que representa la proyección en el espacio nulo de las variables focus.

Mediante este procedimiento los parámetros del modelo sin restricciones (ecuaciones (3) y (4)) pueden obtenerse de manera sencilla para cada modelo. Pero al realizar esto obtenemos un conjunto de parámetros y modelos, sobre los cuales no se tiene certeza si deben o no estar en la especificación definitiva. Por esto, se plantea una estrategia para calcular la probabilidad de que un modelo determinado sea el correcto.

Para esto como primer paso, se define una distribución de probabilidad inicial (prior) sobre el conjunto de modelos, donde su función de probabilidad mide la probabilidad de que el modelo sea correcto. Esta distribución tiene como una de sus principales características que se define de forma previa a contrastar con los datos muestrales y se representa como p(Mi).

Luego de esto, parece coherente utilizar toda la información disponible sobre la variable de interés para calcular la probabilidad que un determinado modelo Mi sea el correcto. Por lo tanto, se plantea una distribución de probabilidad condicional a la información disponible, la cual es llamada distribución posterior y se representa como p(Mi |y).

Para obtener esta distribución posterior se parte de la siguiente definición de probabilidad condicional:

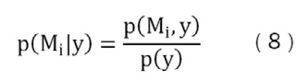
Como p(Mi, y) = p(y, Mi), y al emplear nuevamente la definición de probabilidad condicional se puede sustituir el numerador de la ecuación (8) por p(Mi, y) = p(y| Mi) p(Mi) .

Además, por el teorema de probabilidad total es posible sustituir el denominador por:

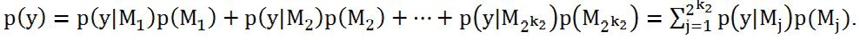
Con lo que la distribución posterior, se representa:

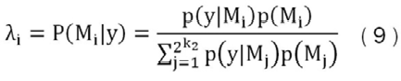
Como se puede apreciar esta distribución depende tanto de la distribución prior como de la probabilidad condicional P(y|Mi), llamada función de verosimilitud marginal. Respecto a la distribución prior, si no se cuenta con información de otras investigaciones o algún criterio de experto sobre el conjunto de modelos, usualmente se asume que todos los modelos tienen la misma probabilidad de ser el modelo correcto, P(Mi ) = 2-k2. Asimismo, al definir la distribución prior de esta manera, se observa que no depende de , por lo que la distribución posterior únicamente dependería de la función de verosimilitud marginal, λi ∝ p(y|Mi) .

Para obtenerla se puede suponer que un determinado modelo Mi es el correcto. Al realizar un proceso similar al anterior se puede hacer algún supuesto sobre la distribución prior de los parámetros.

Por ejemplo, si se asume una prior no informativa sobre β1 y σ2, y una prior Gausiana para β2_i, se obtiene que para un modelo en particular se tiene la probabilidad condicional prior, que es una probabilidad tipo Zellner´s g-prior (Goel,1986), la cual es una distribución normal que depende del hiperparámetro g, el que está relacionado con la importancia que se le quiera brindar a la información contenida en la prior. En este trabajo se sigue lo propuesto por Fernández, Ley y Steel (2001) donde se utiliza una regla expresada en la ecuación (12) para determinar este hiperparámetro. En donde se genera la siguiente probabilidad condicional prior:

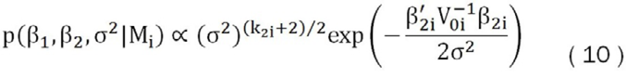
Donde:

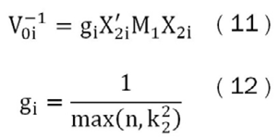
Como resultado del supuesto de normalidad, se obtiene la siguiente distribución de verosimilitud gamma inversa para los parámetros:

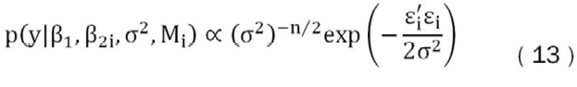
Ahora si se combina (10) y (13), y el resultado se usa en (9), la distribución posterior del conjunto de modelos toma la siguiente forma:

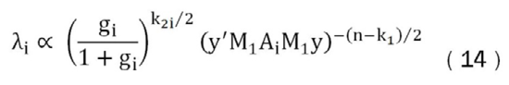
Donde:

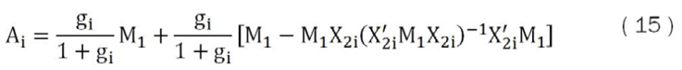
Consecuentemente, de las ecuaciones (14) y (15) se observa que la probabilidad posterior de cada modelo depende básicamente de la matriz X2_i de variables auxiliares y del hiperparámetro gi, e indirectamente de la matriz X1, las que modifican el valor de Ai y con esto la probabilidad posterior.

Dado que ahora se cuenta con un valor para la probabilidad de cada modelo, se puede agregar para cada parámetro estimado sobre el total de modelos posibles calculados, con la utilización de un promedio ponderado por la probabilidad posterior de cada modelo, como se muestra:

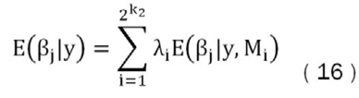
Estas agregaciones de modelos han mostrado buenas propiedades predictivas como se ha demostrado en diversos estudios. Por otro lado, estos modelos cuentan con algunas limitaciones principalmente relacionadas con el número de variables auxiliares, dado que si se cuenta con un número considerable de variables auxiliares el proceso de estimación puede resultar lento, al igual el hecho de que no se utiliza ningún criterio de optimización en la elección de la prior sobre β2.

Weighted Average Least Squares

Otra estrategia que puede ser utilizada es el propuesto por De Luca y Magnus (2011), la cual se basa en una ortogonalización de la matriz de variables auxiliares, que permite reducir de manera considerable la cantidad de modelos por estimar. Dado lo anterior se llega a formalizar únicamente k2 modelos, reduciendo significativamente el tiempo de estimación.

Así se siga la siguiente ortogonalización:

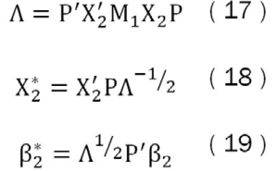
Donde P es una matriz de k2 x k2 formada por los vectores propios de la matriz X’2M1X2 (matriz de la proyección de X2 ortogonal a X1), Ʌ es una matriz diagonal de k2 x k2 , donde en la diagonal se encuentran los valores propios de la matriz X’2M1X2.

Además se puede probar de (18) que X’2^*M1X2^* = Ik2 y obtener los parámetros originales de β2 de (19), como β2 = PɅ-1/2β^*2.

Luego de realizar esta ortogonalización se estima el modelo no restringido mediante MCO como sigue:

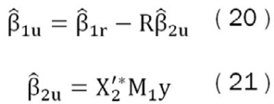
Donde:

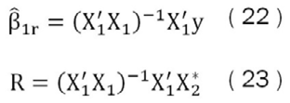
Se desprende que (22) es el vector de parámetros de tamaño k1 x 1 de una regresión por MCO de explicada por las variables focus. Además, la ecuación (23) representa el vector de parámetros de tamaño k1 x 1 de una regresión MCO de X^*2 explicada por las variables focus.

Ahora si se define una matriz Si = (Ik2-k2i,0) de tamaño k2 x (k2 − k2i), que busca capturar las restricciones que se imponen a cada modelo Mi sobre los parámetros de las variables auxiliares. Se puede cambiar las ecuaciones (20) y (21) por:

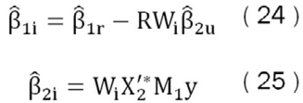
Donde:

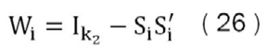
Así Wi es una matriz diagonal de unos y ceros de tamaño k2 × k2, donde si un elemento en particular es igual a cero se considera que la restricción está activa y por lo tanto, en este modelo la variable auxiliar respectiva tiene una restricción y se supone igual a cero, lo opuesto en el caso donde se encuentre un uno.

Esta matriz diagonal genera que las k2 variables auxiliares sean independientes, lo que admite que todos los modelos que contienen un X^*2i en particular, tengan el mismo β^*2i independiente de cuales sean las otras variables auxiliares por consideradas.

Por otro lado, este método de estimación permite utilizar como prior sobre las variables auxiliares otro tipo de distribuciones como la de Laplace o Subotin, las cuales han demostrado propiedades importantes de equivalencia en las estimaciones8.

Factores dinámicos

Además de preocuparse por la incertidumbre propia sobre la especificación del modelo, interesa reducir la indecisión sobre cuáles variables utilizar a la hora de la estimación. Así, al disponer de una gran cantidad de información que puede llegar a emplearse como variables focus o auxiliares, puede resultar relevante usar alguna técnica que permita disminuir este número de variables buscando tener una pérdida mínima de información.

De esta manera, para dar solución a lo anterior se propone utilizar la técnica de estimaciones con factores dinámicos, que no es otra cosa que regresiones donde las variables explicativas son los componentes principales9 obtenidos de un análisis de componentes principales (ACP). Dichos componentes son variables sintéticas que se caracterizan por ser combinaciones lineales de las variables originales, pero con la ventaja que en un número reducido de variables se logra explicar un alto porcentaje de la variabilidad del conjunto de variables originales.

De esta forma si se pueden sustituir las variables focus y auxiliares por un número limitado de componentes principales, como se propone a continuación.

Donde F1 es una matriz que está formada por los componentes principales que se consideran focus y F2i es la matriz formada por los componentes principales considerados auxiliares.

Selección de variables y datos utilizados

Dada la importancia que tiene la adecuada medición de la inflación a la hora de tomar decisiones de política monetaria, y en especial para el BCCR poder predecir sus valores futuros de manera precisa y oportuna, resulta fundamental escoger cuál es la medida de precios que se debe seguir y determinar las variables que expliquen su comportamiento.

Por lo tanto, dado el rezago con que puede afectar la política monetaria las variables reales de la economía y con esto la estructura de precios, se vuelve fundamental que la medida de inflación utilizada permita seguir los movimientos de más mediano plazo de los precios, para intentar evitar algunos desequilibrios de muy corto plazo.

Por esto, las medidas que se proponen son la inflación general medida por el índice de precios al consumidor (IPC), indicador elaborado por el Instituto Nacional de Estadística y Censos (INEC), además de la inflación de media truncada, indicador elaborado por el BCCR, el cual se basa en el IPC, pero elimina de su cálculo aquellos productos que presenten variaciones de precios más atípicas (Esquivel, Rodríguez y Vásquez, 2011)10.

Datos utilizados

Los datos utilizados para la aplicación empírica de las técnicas bayesianas consisten en 52 variables mensuales de la economía costarricense todas disponibles desde el mes de enero del año 1999 al mes de noviembre 2014. En todos los casos se utilizan datos no desestacionalizados, en términos reales, centrados y estandarizados11.

Dentro de las variables utilizadas se encuentran once12 de los grupos de productos que componen el IPC, además de agregaciones particulares de bienes y servicios, transables o no transables, regulados y no regulados, entre otros. Conjuntamente, se utilizaron otros índices de precios como el índice de precios al productor industrial (IPPI), índice de bienes pecuarios e índice de granos básicos.

Por otra parte, para capturar algunas presiones internacionales sobre la inflación doméstica se incluyeron variables como la inflación de los socios comerciales, inflación de los Estados Unidos de América (EUA), crecimiento de EUA, tipo de cambio real, tipo de cambio nominal entre el dólar y el colón, precios del petróleo crudo tipo West Texas Intermediate (WTI), así como un cóctel de precios de hidrocarburos de referencia para la economía costarricense y la tasa de interés del London Interbank Offered Rate (LIBOR) a seis meses.

Además, se incluyen algunas variables macroeconómicas relacionadas con la curva de Phillips13 como lo son la brecha del producto, índice mensual de actividad económica (IMAE), datos de empleo14, entre otras. Así como, variables utilizadas en las teorías monetarias de inflación como la base monetaria, emisión monetaria, M1 y el medio circulante.

Más aún, se agregaron algunas variables relacionadas con el crédito al sector privado (separado en actividades empresariales y para consumo) y la tasa de política monetaria como medidas indirectas de las restricciones monetarias. Aparte de algunos indicadores del sector real como exportaciones y actividad manufacturera.

En el Anexo 1 se presentan en detalle todas las variables incluidas en las estimaciones como las trasformaciones efectuadas para que estas fueran estacionarias. Las pruebas de estacionariedad no se presentan por razones de espacio, pero están disponibles mediante solicitud a los autores.

Ahora dada la gran variedad y número de variables con las que se cuenta, tal y como se mencionó previamente se utiliza el método ACP para reducir el número de variables para aprovechar la correlación que existente entre ellas. Luego de generar los componentes principales para toda la muestra se estima una matriz de correlaciones (ver Tabla 1) de las variables originales (normalizadas y estandarizadas) con la excepción del IPC, y la inflación de media truncada, respecto a los primeros cinco componentes principales. Con el objetivo de poder apreciar con qué variables se encuentra más correlacionada cada componente principal.

En esta tabla 1 se puede apreciar una fuerte correlación entre el primer componente principal con algunos grupos del IPC, como lo son los artículos de la vivienda y servicios domésticos, comidas y bebidas fuera del hogar; y alimentos y bebidas no alcohólicas, todos con correlaciones positivas. Al igual, este primer componente está fuertemente correlacionado con otros índices como IPC sin combustible, bienes no regulados; así como no regulados sin café; bienes no transables, bienes transables sin combustible e índice de precios de los servicios. Todas ellas con correlaciones positivas y mayores al 60%.

El segundo componente se encuentra correlacionado principalmente con variables relacionadas con agregados monetarios como la emisión monetaria, base monetaria y medio circulante, al igual que el crédito al sector privado.

El tercer componente se encuentra correlacionado con el transporte, bienes transables y bienes regulados; además de la inflación internacional de socios comerciales y el índice de precios al productor industrial (IPPI). Mientras el cuarto componente esta correlacionado negativamente con los bienes regulados sin combustible, los bienes regulados, servicios regulados; y el alquiler y servicios de la vivienda. Mientras el último componente se encuentra correlacionado con la inflación internacional, inflación de Estados Unidos, variación del WTI y tipo de cambio real.

Es importante destacar que al realizar la descomposición de los datos mediante el análisis expuesto, los componentes resultantes además de estar correlacionados con las variables originales, cuentan con ciertas características que se detallan a continuación:

i) Tienen media cero, como resultado de la normalización de los datos.

ii) La varianza de cada componente principal es igual al valor propio correspondiente al vector propio de donde se obtuvo.

iii) Los componentes principales tienen cero correlaciones entre ellos.

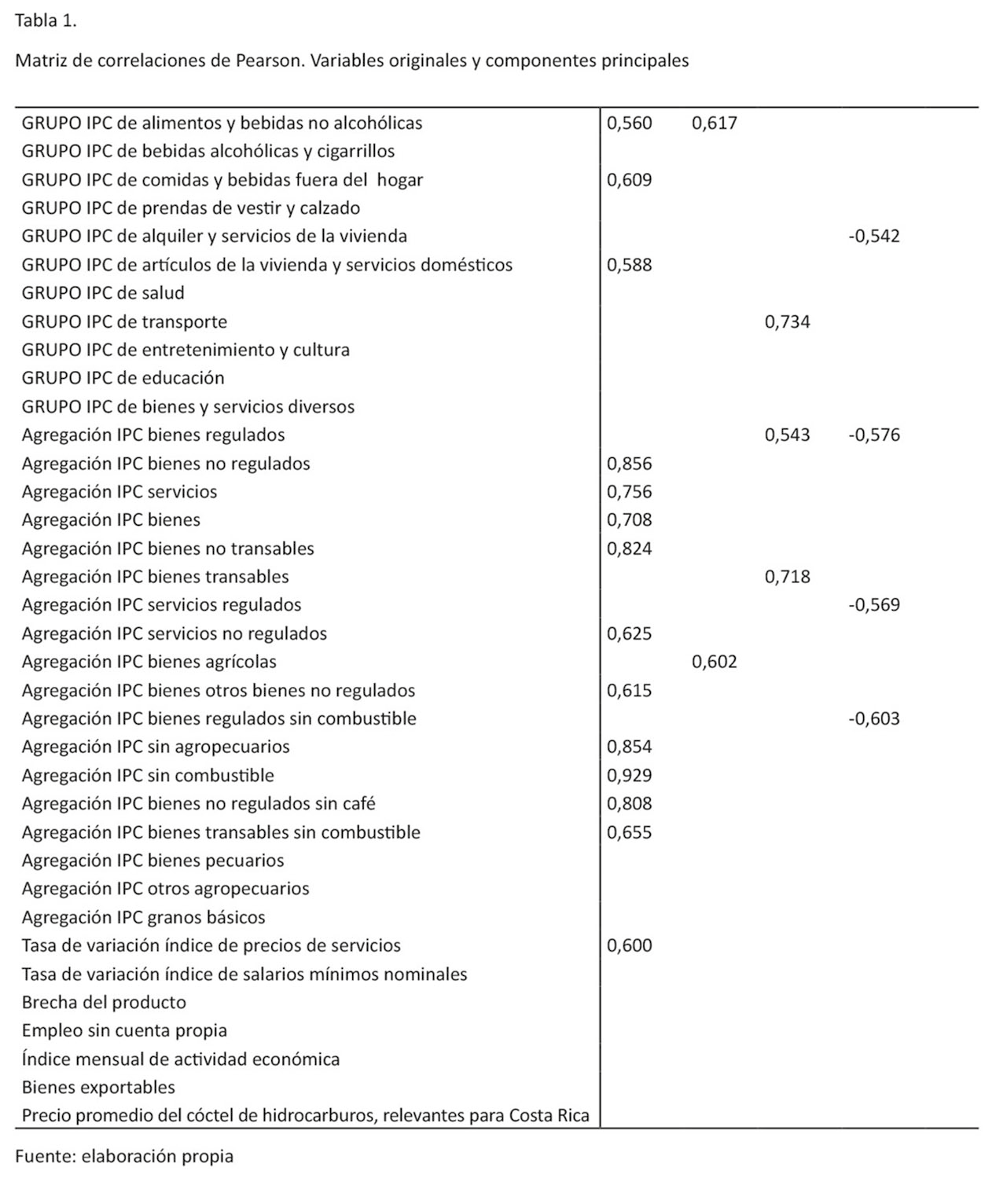
Ahora dado que el interés es buscar la mejor representación posible de los datos, esto se entiende como buscar la manera de recoger la mayor cantidad de la variabilidad de los datos originales en una nueva representación. Se presenta en la tabla 2 la varianza que acumula cada componente principal respecto a la varianza total de los datos.

Es relevante indicar que en la tabla 2, únicamente se presentan los componentes principales cuya variación sea mayor a uno, ya que con este criterio de selección asegura que la incorporación de cada componente esté contribuyendo a la explicación del conjunto de variables.

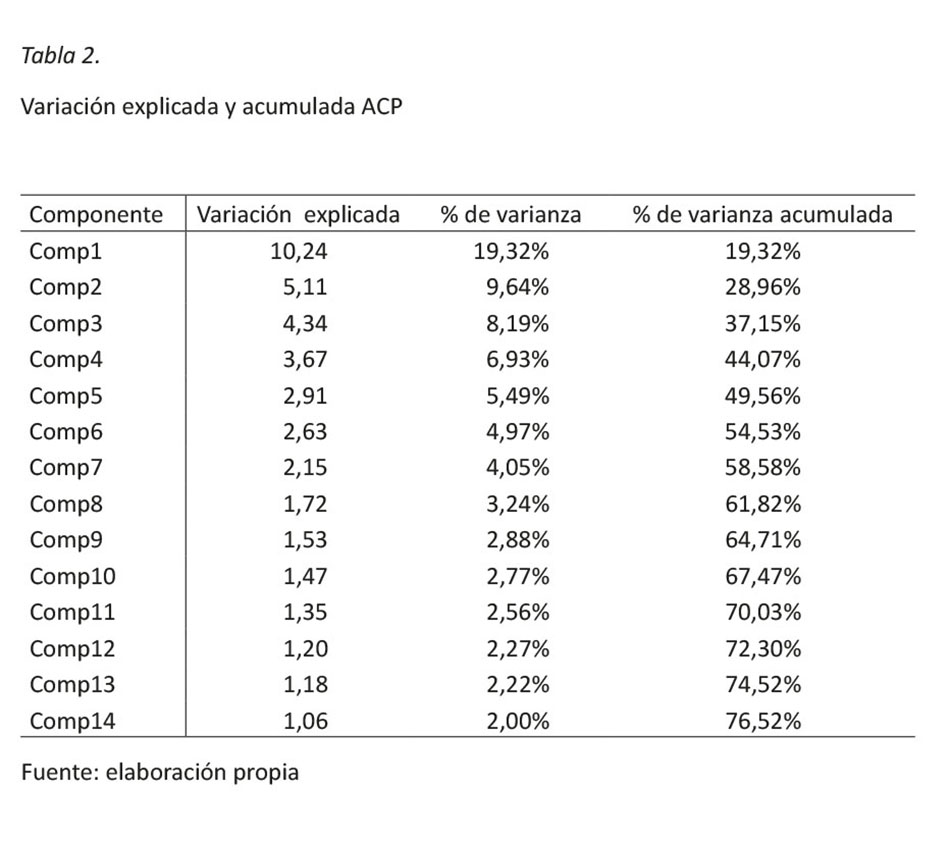
Se puede apreciar que con únicamente once componentes principales se acumula cerca del 70% de la variabilidad total del conjunto de datos. Por lo tanto, con este método de reducción de la información se puede garantizar que con este pequeño número de variables sintéticas se está representando el conjunto de 52 variables, en donde se deja sin explicar solamente un 30% de la variabilidad de ellas.

Por otro lado, en la tabla 2 se observa que cada componente explica un porcentaje cada vez menor de la variabilidad total de los datos, y el componente 1 es el que tiene la mayor proporción de la variabilidad explicada con alrededor de un 20%. Como se analizó anteriormente, este componente se caracteriza por estar altamente correlacionado con algunos grupos del IPC y otras agregaciones, por lo tanto, se puede estar seguro que estas variables van a encontrarse bien representadas por medio de este componente. El mismo análisis se puede hacer con los demás componentes principales y con su respectiva relación con las variables originales.

Resultados obtenidos

Para analizar la capacidad predictiva de estos modelos, se realiza un ejercicio dentro de una muestra cuyo objetivo es evaluar la calidad de los pronósticos provenientes tanto de las técnicas bayesianas como de los modelos de factores dinámicos, en comparación con otro tipo de modelos comúnmente utilizados para estos fines, como lo son los modelos autorregresivos. Para esto se empleará una medida de la calidad de los pronósticos como el error cuadrático medio.

Para realizar esto se dividirá la muestra en dos ventanas, una llamada ventana de estimación, que se extiende desde el mes de enero de 1999 a enero del año 2011, y otra ventana llamada ventana de prueba, la que se extiende del mes de febrero del año 2011 al mes de noviembre del 2014.

Asimismo, la ventana de estimación es una ventana rodante, esto quiere decir que dentro de ella se calcularán tanto los componentes principales, con los parámetros de las regresiones utilizadas. Esta ventana se moverá un periodo a la vez, donde en cada paso se incluirá una nueva observación y se dejará la última observación utilizada en el paso previo, hasta llegar al último mes en consideración.

En cada uno de las iteraciones se utilizarán los componentes principales para estimar las variables de interés, en donde se usan las técnicas de BMA, WALS, factores dinámicos y un modelo autorregresivo; y con estas estimaciones se realizarán pronósticos de 1,2, 3,…, 6 y 12 meses hacia adelante a partir de la última información disponible.

Es importante recordar que para cada ventana de estimación se contará con una importante cantidad de posibilidades, dado que cada periodo cuenta con un conjunto diferente de componentes principales, de los que se deben definir cuales utilizar, además de cuáles tratar como variables focus y variables auxiliares; asimismo, definir si se utilizan rezagos. Por ello, se probarán diferentes especificaciones y se tomarán en cuenta diferentes números de rezagos para los primeros tres componentes principales, así como diferentes números de rezagos de la variable dependiente.

Este procedimiento se realiza con el objetivo de simular un experimento en tiempo real, que consta en intentar replicar las condiciones que tendría un individuo a la hora de pronosticar la inflación si se ubicara en el último periodo de la ventana de estimación y su interés fuera proyectar la inflación para h = 1, ..., 6 y 12 meses hacia adelante.

Así, para cada periodo y para cada modelo se podrá proyectar los valores de inflación para diferentes horizontes en la ventana de prueba, lo cual se puede representar:

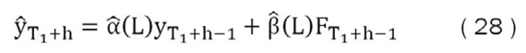
Donde α̂(L) es el polinomio de rezagos de la variable dependiente y β̂(L) es el polinomio de rezagos de los componentes principales. Así, para efectos de la estimación de este trabajo se considera el primer polinomio de rezagos las variables que formarán el vector de variables consideradas focus con un máximo de cuatro rezagos de la variable dependiente mientras el segundo polinomio representa el vector de variables auxiliares formado por los primeros tres componentes principales con un máximo de cuatro rezagos.

Para evaluar la calidad de los pronósticos se debe establecer un indicador que permita comparar el resultado de los diferentes modelos propuestos. Para esto, se utilizará el error cuadrático medio (ECM), que se define como el promedio del error de pronóstico en la ventana de prueba para cada horizonte de proyección (h = 1, ..., 6 y 12) y cada tipo de modelo.

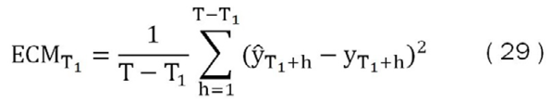
Donde T1 representa la última observación de la ventana de estimación, ŷT1+h son los valores pronosticados h pasos hacia adelante desde T1, y yT1+h son los valores observados de la variable de interés.

Para poder proyectar tanto la inflación de media truncada como la inflación que se obtiene del índice de precios al consumidor, y al intentar simular un ejercicio en tiempo real los individuos tendrían que tomar una decisión sobre si proyectar estas series ya sea de manera directa o mediante un proceso iterativo, el cual requiere realizar algún supuesto sobre el comportamiento futuro de los predictores.

Por lo tanto, si se usa el segundo método y se realizan dos tipos de supuestos sobre las variables originales, buscando que estos supuestos sean fácilmente replicables en futuras ocasiones, se podrán utilizar los valores proyectados de las variables originales como individuos suplementarios en el ACP15 y con esto tener las proyecciones de las variables predictoras.

Así, el primer supuesto utilizado es hacer crecer a las variables originales a la tasa de crecimiento promedio de los últimos ocho meses para todo el periodo restante (creci), mientras que el segundo supuesto es que las variables originales se van a quedar fijas en su último valor observado (fija).

Los resultados obtenidos de las proyecciones de 1, 2,…, 6 y 12 meses se presentan en la tabla 3. Donde para una presentación más intuitiva se reescalan los ECM respecto a un modelo univariado (AR1). De esta manera cualquier valor menor que 1 se interpreta como un método de estimación que presenta un ECM menor que el generado por este modelo autorregresivo. Por ejemplo, en la tabla 3 se observa para el resultado ubicado en la primera fila y la primera columna, resultado correspondiente al método de estimación de BMA con predictores fijos y con un rezago (k = 1), presenta errores de pronóstico 3,9% menores a los que produce un modelo autorregresivo un periodo hacia adelante.

Se puede apreciar en la tabla 3, que para la mayoría de los horizontes de proyección así como para los métodos de estimación propuestos presentan resultados que superan los producidos por un modelo autorregresivo, lo cual presenta resultados mejores de hasta un 30%, en donde los horizontes de 2, 3, 4 y 12 meses son los que presentaron un mejor desempeño en el caso de la inflación, y los de 1 y 2 meses en el caso de la inflación de media truncada.

16

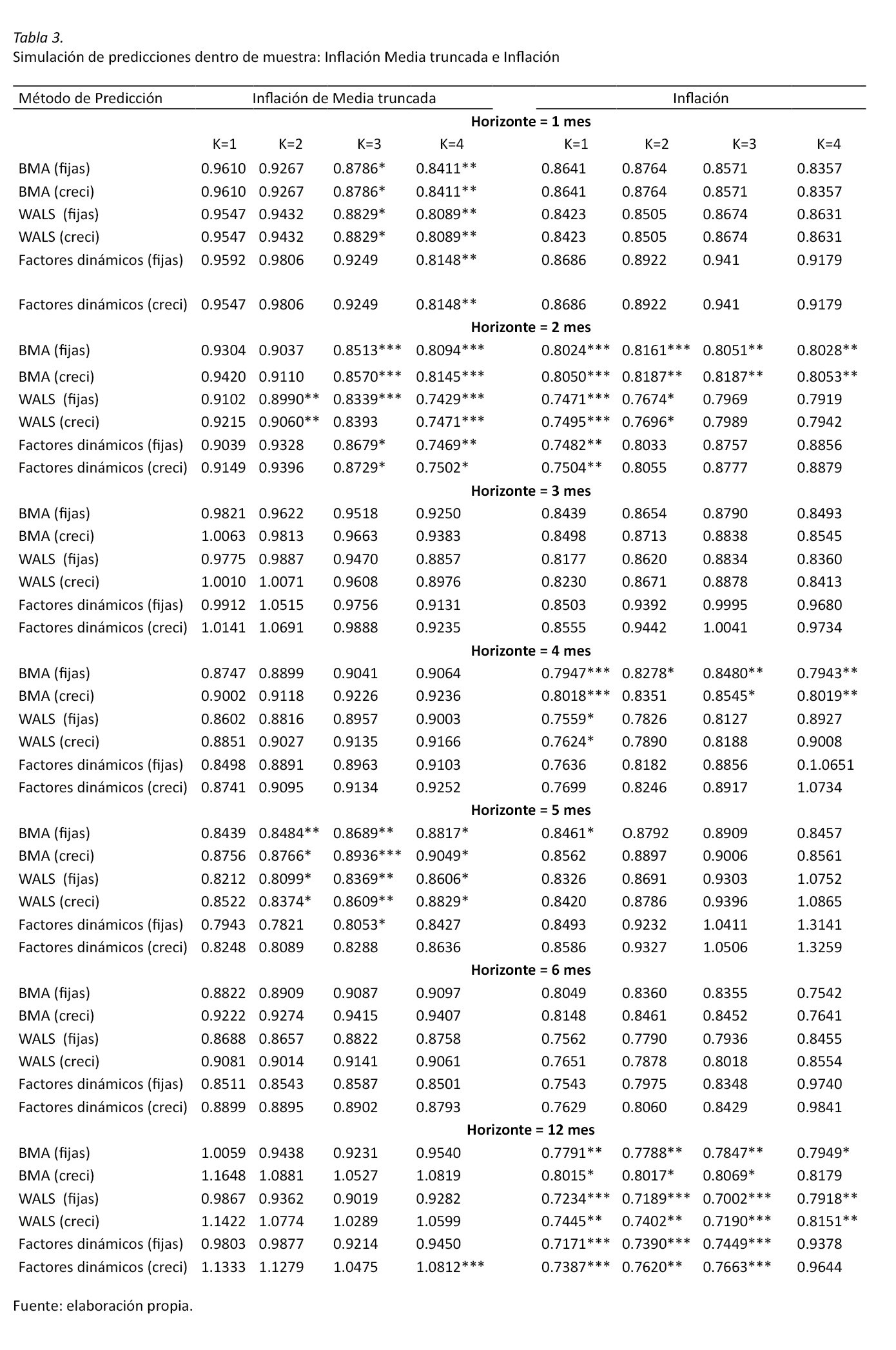
Es destacable el buen desempeño que tiene todos los métodos para la inflación respecto pronósticos a 12 meses. Se observa que para muchos modelos y rezagos utilizados presentan un desempeño estadísticamente superior al de un modelo autorregresivo. Esto es de especial relevancia dado el interés que tiene el BCCR en obtener pronósticos oportunos y confiables de esta variable en este horizonte en específico, con el fin de definir adecuadamente la política monetaria.

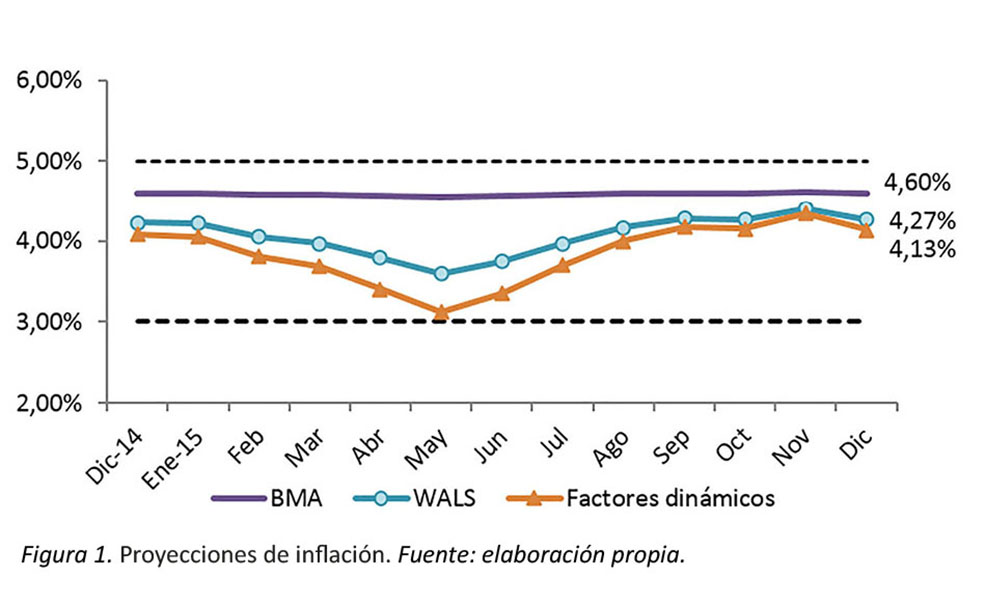
La calidad de los pronósticos a 12 meses que estos modelos pueden ofrecer se evalúa con la información que contiene la tabla 4. Las proyecciones de la inflación general se elaboran con la utilización de datos actualizados al mes de noviembre del año 2014 y se generan proyecciones de lo que se espera sería la inflación interanual para horizontes de 1 hasta 12 meses a partir del último dato disponible, esto permite comparar la proyección con el dato observado a diciembre, enero y febrero 2015

17

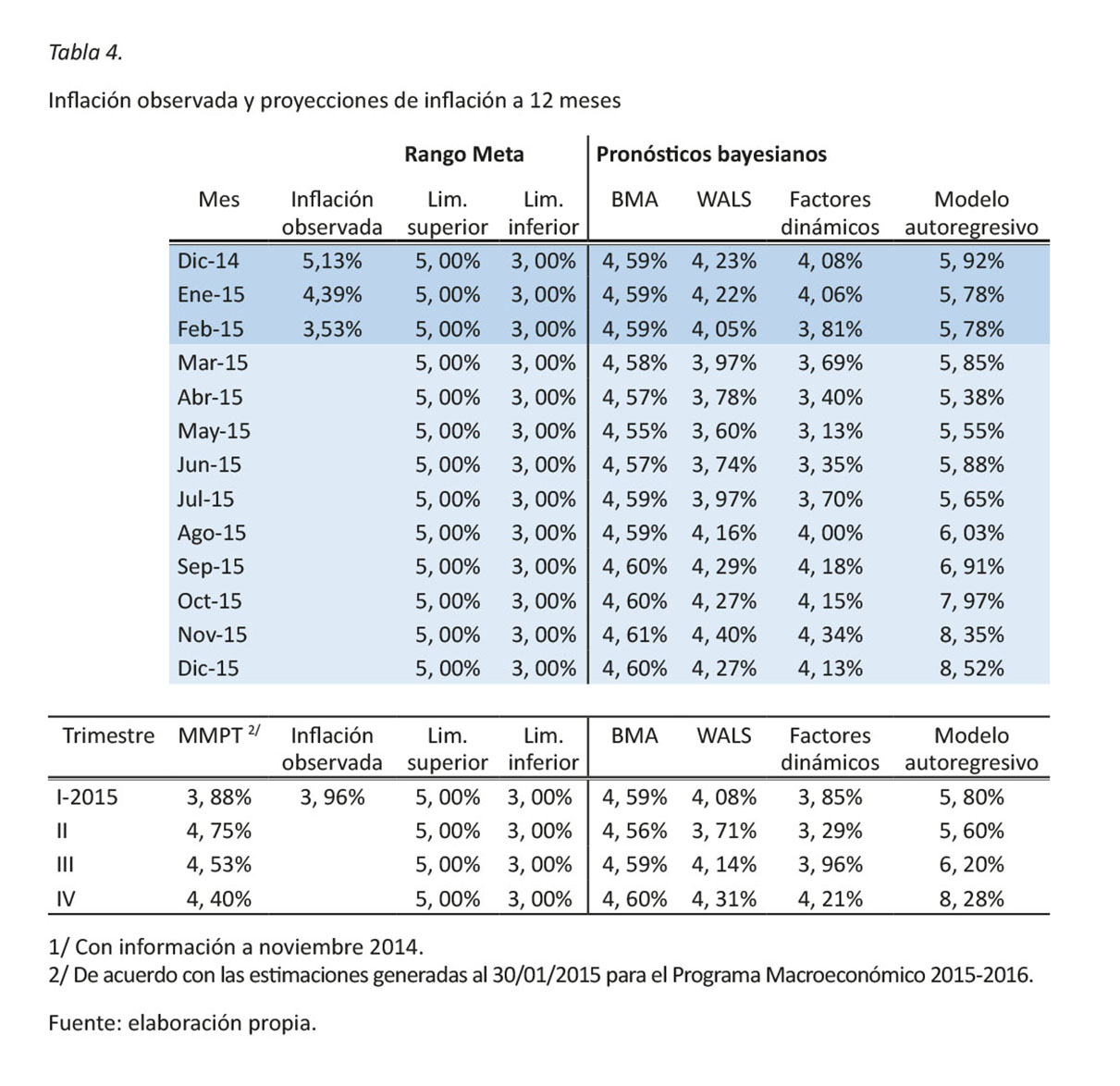
Como se puede apreciar la proyección de la inflación general que se obtiene a partir de los modelos no se aleja mucho de la inflación observada, siendo la proyección de inflación obtenida mediante la técnica WALS y de factores dinámicos las que desvían menos en relación con lo observado. A pesar de este buen resultado, es necesario destacar que estas estimaciones no representan un ejercicio de proyección en tiempo real, sino la validación del uso de técnicas bayesianas para generar pronósticos.

Resulta importante mencionar que el conjunto de información utilizada no incorpora los efectos de las reducciones en el precio de los combustibles que se registraron durante los primeros meses de 2015 y que modificaron el patrón de comportamiento de las 51 variables utilizadas para la construcción de las componentes principales.

Otro resultado interesante y que se revalida con la proyección central del MMPT para el Programa Macroeconómico 2015-2016 es que para todo el periodo de estimación, la inflación proyectada está dentro del rango meta definido por el BCCR.

18

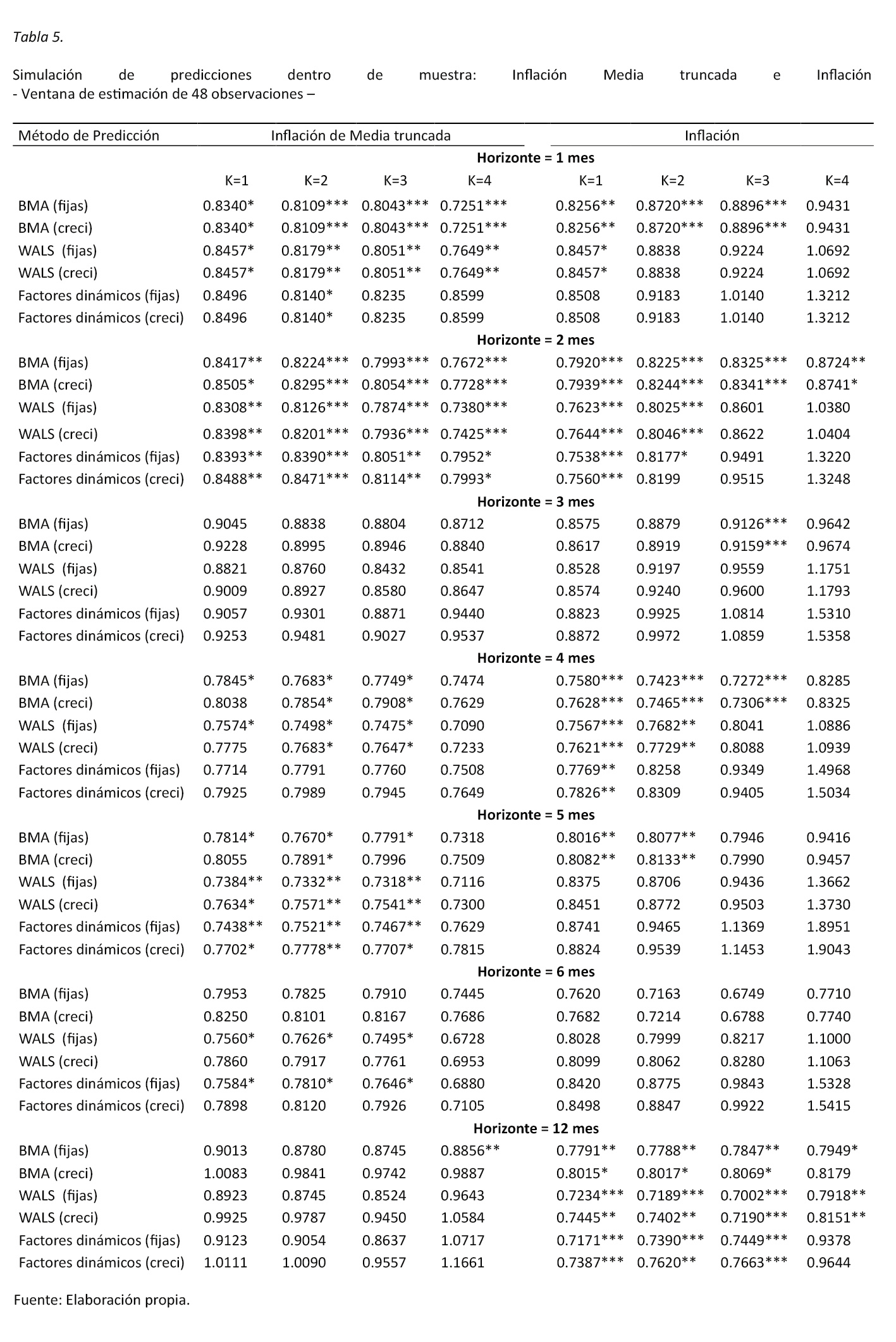
Para probar la coherencia de los resultados se realizaron diversas pruebas, donde se varió tanto el tamaño de la ventana de estimación como el punto de inicio de la ventana de pruebas y se encontró que los resultados se mantienen.

Un ejemplo de estas pruebas se presenta en la tabla 5, donde se realiza el mismo ejercicio de estimación anterior, pero ahora con el cambio en la ventana de estimación a una de 48 observaciones. En la tabla 5 se aprecia que los resultados son coherentes respecto a los encontrados anteriormente. Se puede apreciar una importante bondad de ajuste en las proyecciones, por ejemplo de la inflación de media truncada para los horizontes de 1, 2 y 5 meses, mientras en el caso de la inflación general los métodos son superiores en los horizontes de 2, 4 y 12 meses.

Por otro lado, y de acuerdo con la información contenida en las tablas 3 y 5, se aprecia que las proyecciones de los modelos bayesianos presentan para horizontes relativamente más extensos de estimación mejores resultados que los propios modelos de factores dinámicos. Además se observa que no existe una ventaja absoluta de ninguno de los dos métodos bayesianos propuestos.

Finalmente, se puede anotar que para algunos rezagos los métodos de factores dinámicos tienden a perder su buen desempeño y genera que los resultados sean dependientes del número de rezagos utilizados en las especificaciones (por ejemplo, el desempeño de los factores dinámicos en la tabla 3 con un horizonte de predicción de 5 meses).

19

Conclusiones

En línea con las necesidades de información precisa y oportuna que requiere el BCCR para la toma de decisiones de política monetaria que le permita mantener una inflación baja y estable, el presente trabajo propone herramientas complementarias para elaborar pronósticos de inflación de corto y mediano plazo, a partir de un conjunto de variables cuyo rezago en relación con el periodo t es 60 días.

Así, se propone la utilización de dos técnicas bayesianas, como lo son el Bayesian Model Averaging y Weighted Average Least Squares, así como de un modelo de factores dinámicos, con el objetivo de proponer modelos alternativos que vengan a enriquecer las estimaciones que realiza el banco.

De esta manera se realiza un ejercicio dentro de una muestra para probar que estás técnicas brindan pronósticos estadísticamente superiores a las que pueden entregar un modelo univariado. Estos resultados son especialmente significativos para el caso de la inflación a un horizonte de 12 meses, lo cual es relevante en términos de su utilidad en las decisiones de política monetaria.

Además, estos pronósticos son robustos ante cambios en la longitud de ventana de estimación y ante cambios en el periodo de inicio de la estimación.

Como trabajos futuros, los resultados de esta investigación pueden ser complementados y ampliados con la construcción de gráficos de abanico para la inflación a partir de estimaciones generadas por cada modelo; una línea de investigación importante por desarrollar se puede centrar en el análisis de la función de probabilidad posterior de cada modelo. Lo anterior permitirá identificar en cada momento del tiempo cuales son las variables que tienen la mayor probabilidad de explicar el fenómeno inflacionario a corto plazo.

A la luz de los resultados obtenidos se recomienda que las proyecciones de inflación mediante técnicas bayesianas sean incorporadas como insumo relevante para el seguimiento de la programación macroeconómica que realiza el BCCR.

Referencias Bibliográficas

Álvarez, C., & Torres, C. (2011). Modelos de Inflación de Corto Plazo para los Sectores Transable y No Transable de la Economía Costarricense (Documento de Investigación No. 04-2011). Recuperado del sitio de internet del Banco Central de Costa Rica, Departamento de Investigación Económica: http://www.bccr.fi.cr/investigacioneseconomicas/politi-camonetariaeinflacion/Modelos_inflacion_cp_sectores-_transable_y_no_transable_economia_costarricense.pdf

Brissimis, S., & Magginas, N. (2008). Inflation Forecast and the New Keynesian Phillips Curve, International Journal of Central Banking. Recuperado de http://www.ijcb.org/journal/ijcb08q2a1.htm

Danilov, D., & Magnus, J. (2004). Forecast Accuracy After Pretesting with an Application to the Stock Market, Journal of Forecasting, 23(4), 251-274. http://dx.doi.org/10.1002/for.916

De Luca, G., & Magnus, J (2011). Bayesian Model Averaging and Weighted Average Least Squares: Equivariance, Stability, and Numerical Issues (Center Working Paper No. 2011-082). http://dx.doi.org/10.2139/ssrn.1894610

Diebold, F., & Mariano, R. (1995). Comparing predictive accuracy, Journal of Business and Economic Statistics 13(3), 253-263. http://dx.doi.org/10.1080/07350015.1995.10524599

Esquivel, M., Rodríguez, A., & Vásquez, J. (2011). Medias truncadas del IPC como indicadores de inflación subyacente en Costa Rica (Documento de investigación No. 01-2011). Recuperado del sitio de internet del Banco Central de Costa Rica, Departamento de Investigación Económica: http://www.bccr.fi.cr/investigacioneseconomicas/politi-camonetariaeinflacion/Medias%20truncadas_del_IPC_co-mo_indicadores_de_inflacion_subya-cente_en_CR.pdf

Fernández, C., Ley, E., & Steel, M. (2001). Benchmarks priors for Bayesian model averaging, Journal of Econometrics 100(2), 381-427. http://dx.doi.org/10.1016/S0304-4076(00)00076-2

Goel, P. (1986). On Assessing Prior Distributions and Bayesian Regression Analysis with g-Prior Distributions. En Zellner, A (Ed), Bayesian Inference and Decision Techniques: Essays in Honour of Bruno de Finetti (Studies in Bayesian Econometrics and Statistics, Vol.6). Recuperado de http://www.amazon.com/Bayesian-Inference-Decision-Techniques-Econometrics/dp/0444877126

Hoffmaister, A., Saborío, G., & Vindas, K. (2000). Proyecciones de Inflación: Innovaciones en los Precios Agrícolas y Regulados, y Ajustes (Nota de Investigación No. 7-00). Recuperado del sitio del Banco Central de Costa Rica, Departamento de Investigación Económica. Recuperado de http://www.bccr.fi.cr/investigacioneseconomi-cas/politicamonetariaeinflacion/Proyecciones_Inflacion-,_Innovaciones_Precios_Agricolas_Regulados_Ajustes.pdf

Magnus, J., Powell, O., & Prüfer, P. (2010). A comparison of two model averaging techniques with an application to growth empirics, Journal of econometrics 154(2), 139-153. http://dx.doi.org/10.1016/j.jeconom.2009.07.004

Magnus, J., & Durbin, J. (1999). Estimation of regression coefficients of interest when other regression coefficients are of no interest, Econometrica Journal of Econometric Society 67(3), 639-643. http://dx.doi.org/10.1111/1468-0262.00040

Muñoz, E. (2008). Validación del Modelo Univariable de Inflación empleado en la Combinación de Pronósticos (Informe técnico DIE-08-2008). Recuperado del sitio del Banco Central de Costa Rica, Departamento de División Económica: http://www.bccr.fi.cr/investigacioneseconomicas/politi-camonetariaeinflacion/Validacion_Modelo_Univariable_In-flacion_empleado_Combina-cion_Pronosticos.pdf

Rodríguez, A. (2009). Evaluación del modelo lineal pass-through para la proyección de inflación dentro del régimen de banda cambiaria (Documento de Investigación 07-2009). Recuperado del sitio de internet del Banco Central de Costa Rica, Departamento de Investigación Económica: http://www.bccr.fi.cr/investigacioneseconomicas/politi-camonetariaeinflacion/Evaluacion_modelo_lineal_pass-_through_proyeccion_inflacion_regimen_banda_cambia-ria.pdf

Steel, M. (2014). Bayesian model averaging and forecasting. Recuperado de http://www2.warwick.ac.uk/fac/sci/statistics/staff/aca-demic-research/steel/steel_homepage/publ/bma_forecast.pdf

Vindas, A. (2011). Validación del modelo ARMA para la proyección de la inflación en Costa Rica (Serie Documentos de Trabajo No. 03-2011). Recuperado del sitio del Banco Central de Costa Rica, Departamento de Investigación Económica: http://www.bccr.fi.cr/investigacioneseconomicas/poli-ticamonetariaeinflacion/Validacion_del_modelo_ar-ma_para_la_inflacion.pdf

1/ 1: Variable en diferencia, 2: Variable en diferencia logarítmica.