Didier Alberto Castro Méndez1

Universidad Latinoamericana de Ciencia y Tecnología

San José, Costa Rica

dcastro@ulacit.ac.cr

Introducción

El ámbito afectivo en la educación matemática se refiere a que sentimientos, estados de ánimo y actitudes tienen un impacto directo en el rendimiento académico (McLeod, 1989, 1992, según se cita en Pedrosa, 2020). Las creencias, modeladas por experiencias pasadas, y las emociones, como respuestas afectivas automáticas, influyen en el rendimiento en matemáticas (Esquivel et al., 2008, según se citan en Pedrosa, 2020; Gil et al., 2005, según se citan en Pérez, 2012). Esta conexión afectiva incide en el comportamiento estudiantil (McLeod, 1989, según se cita en Castro, 2023). Las creencias matemáticas influyen en la percepción del éxito o fracaso, de modo que impactan la ansiedad matemática y el rendimiento académico (Delgado-Monge et al., 2020). Las vivencias de aprendizaje matemático, positivas o negativas, moldean creencias, actitudes y emociones estudiantiles, que afectan su conducta y capacidad de aprendizaje (García y Lahuerta, 2020). Los docentes desempeñan un papel esencial, al motivar a los estudiantes y crear expectativas con línea positiva (León et al., 2020, según se citan en García y Lahuerta, 2020). Las actitudes también son cruciales en el proceso de enseñanza-aprendizaje, pues influyen en el comportamiento y las interacciones sociales estudiantiles (Allport, 1935, según se cita en Pedrosa, 2020), hecho que condiciona la disposición y eficacia en matemáticas (Hidalgo et al., 2013, según se citan en Delgado-Monge et al., 2020).

Este trabajo amplía la comprensión sobre la ansiedad matemática en una universidad privada de Costa Rica, al establecer vínculos significativos con investigadores de la región, quienes exploran los aspectos clave en los procesos de enseñanza-aprendizaje de las matemáticas. El problema del estudio se planteó por medio de la siguiente pregunta: ¿Existen diferencias estadísticamente notables entre autoestima, ansiedad y motivación matemáticas en los estudiantes de precálculo de la ULACIT, en función del género y el área de estudio?

El objetivo general de la investigación fue examinar el enlace entre el nivel de autoestima, ansiedad y motivación matemáticas en estudiantes de precálculo de la Sede Metropolitana de la Universidad Latinoamericana de Ciencia y Tecnología, en el I cuatrimestre de 2024, por género y área de estudio. Se tuvieron los propósitos específicos de medir el nivel de autoestima, ansiedad y motivación matemáticas de los alumnos, determinar si existen diferencias estadísticamente significativas en el grado de autoestima, ansiedad y motivación matemáticas que manifiestan los estudiantes, conforme el género y área de estudio, así como establecer si existe relación entre el nivel de promedio de cada variable (autoestima, ansiedad y motivación matemáticas).

Antecedentes

Para este estudio, la ansiedad matemática se define como un estado afectivo caracterizado por sentimientos de tensión, desvalimiento, indefensión y desorden mental frente a situaciones que involucran números o resolución de problemas matemáticos. Esta ansiedad se manifiesta a través de emociones desagradables como el miedo y la inseguridad (Castro, 2023). Respecto a la motivación matemática, Rojas (2018, según se cita en Chiri et al., 2023) la describe como un conjunto de elementos que incrementa el impulso de alcanzar una meta, lo cual implica voluntad, persistencia y trabajo duro. Además, Camposeco (2012, según se cita en Coz, 2019) y Skaalvik et al. (2015, 2012, según se citan en Coz, 2019) exploran el vínculo entre la motivación intrínseca y la confianza en habilidades matemáticas. En cuanto a la autoestima, se define como un constructo psicológico influyente en diversos aspectos de la vida, basado en las autoevaluaciones de uno mismo (Naderi et al., 2021). González-Vázquez (2019) plantea que es la valoración subjetiva de uno mismo, que afecta la percepción personal y la interacción con los demás.

La investigación sobre ansiedad matemática revela hallazgos significativos respecto al género y el área de estudio. Pérez (2012) destaca la complejidad de esta relación, al indicar que, aunque las mujeres suelen experimentar niveles más altos en algunos ambientes, tal asociación puede variar. Delgado-Monge et al. (2020) encuentran que estudiantes en carreras con más cursos de matemáticas muestran menos ansiedad, sin diferencias de género en Costa Rica y España. Nadide (2020) aborda la diferenciación de género en los niveles de ansiedad, observa que los hombres tienden a manifestar niveles más altos y atribuye estas diferencias a la percepción de autoeficacia y los estereotipos de género. Bojorquez et al. (2021) contradicen estudios previos que sugieren que las mujeres tienen más ansiedad matemática, al concluir que la diferencia de género no está directamente relacionada con la ansiedad. Castro y Madrigal (2023) no encuentran discrepancias notables conforme al sexo, pero reportan variaciones importantes por área de estudio, con mayor ansiedad en ciencias empresariales. Aunque trabajos anteriores indican que las mujeres tienden a manifestar mayor ansiedad, Castro y Madrigal (2023) muestran que los estudiantes tienen niveles altos de dicho estado, con un mayor promedio entre las mujeres, de acuerdo con Alfaro y Valverde (2023). Alrededor del 51.20 % de los alumnos muestra un nivel promedio de ansiedad matemática medio, mientras que un significativo 86.07 % experimenta niveles elevados, según lo indicado por Castro (2023). Aunque no hay diferencias estadísticamente significativas según el género, investigaciones previas sugieren que las mujeres tienden a manifestar más ansiedad en esta área. Alfaro y Valverde (2023) señalan que el 55.86 % de los estudiantes tiene un nivel promedio alto de ansiedad, mayormente las mujeres. En contraste, Castro y Madrigal (2023) muestran que el 18.84 % de los estudiantes tiene niveles altos de ansiedad matemática.

En el ámbito educativo, la relación entre género, área de estudio y motivación matemática ha sido objeto de diversos estudios. Suren y Kandemir (2020) destacan la influencia positiva del aliciente en el rendimiento matemático, al observar que estudiantes con alto estímulo tienden a destacar en esta área. Aunque el enlace entre rendimiento y motivación es generalmente positivo, su estudio revela que, en términos de la segunda (hacia las matemáticas), las mujeres superan a los hombres en todos los factores examinados. A pesar de los avances en igualdad de género, persisten diferencias en logros académicos y profesionales. Ortiz-Padilla et al. (2020) confirman la tendencia de mayor motivación matemática entre mujeres; sin embargo, a pesar de esta, muestran una menor preferencia por carreras que incluyan matemáticas, lo que podría limitar sus opciones de estudio y afectar sus alicientes a lo largo del tiempo. En contraste, Pérez (2012) destaca que, aunque las mujeres concluyen la educación superior con mejores resultados, hay un mayor porcentaje de hombres estudiando matemáticas universitarias y obteniendo un mejor rendimiento, lo cual sugiere más motivación a lo largo de sus estudios. Estas perspectivas resaltan la complejidad de las dinámicas de estímulo y género en la educación matemática, que subrayan la importancia de abordarlas para optimizar el apoyo y desarrollo estudiantil.

En el marco de la autoestima y su relación con los procesos de enseñanza-aprendizaje, varios estudios ofrecen perspectivas valiosas. Pérez (2012) encontró una correlación positiva entre la autoconfianza en matemáticas y el rendimiento académico, lo cual propone que los estudiantes con mayor autoconfianza tienden a obtener mejores resultados. Además, Moronta et al. (2019) identificaron diferencias de género en el autoconcepto académico, que favorecen a los hombres en matemáticas y a las mujeres en habilidades verbales, aunque con contradicciones en los resultados. González-Vázquez (2019) agregó que las mujeres muestran una correlación positiva entre la autoestima y competencias como la comunicación oral o la creatividad, en contraste con los hombres, quienes tienden a tener una autoestima más alta en general. Estudios como el de Gezu et al. (2020, según se citan en Cirilo, 2021) revelaron diferencias en la autoestima entre estudiantes de pregrado en Etiopía, al destacar esta característica media-alta en mujeres en comparación con hombres, lo que resalta la influencia de género. Naderi et al. (2021) exploraron la relación entre autoestima, autoconcepto matemático y ansiedad matemática en mujeres; encontraron una asociación relevante entre la primera y el segundo. Chiri et al. (2023) señalaron que una baja autoestima se asocia con niveles más altos de ansiedad en alumnos, lo que puede afectar negativamente su rendimiento académico. Bojorquez et al. (2021) evidenciaron cómo la ansiedad matemática puede influir en la autoestima, especialmente, cuando los estudiantes enfrentan dificultades en la materia. Cirilo (2021) amplió este panorama, al afirmar que una baja autoestima puede desencadenar ansiedad, especialmente en mujeres universitarias, lo que perjudica su rendimiento académico. Javed y Khan (2018, según se citan en Cirilo, 2021) enfatizaron cómo la autoestima influye en la ansiedad y el rendimiento académico, particularmente en mujeres. Estos hallazgos subrayan la necesidad de enfoques pedagógicos que consideren tales interacciones, para promover el bienestar y el éxito académico estudiantiles.

En el campo de la motivación, la actitud hacia las matemáticas y la autoestima, investigaciones como la de Cirilo (2021) destacan cómo una autoestima positiva está asociada con una mayor motivación intrínseca y perseverancia en las metas académicas, ya que influye de manera favorable en la disposición de los alumnos para enfrentar desafíos. Pérez (2012) profundiza en la conexión entre autoestima y motivación, al destacar cómo una autoestima saludable impulsa la motivación, cuando genera confianza en las habilidades y el éxito. Además, la ansiedad matemática puede desmotivar y evadir tareas relacionadas con la materia. Villar et al. (2022) resumen hallazgos sobre factores que influyen en la actitud hacia el aprendizaje de las matemáticas, enfatizando la motivación por instruirse y la metodología de enseñanza como cruciales para impactar positivamente en la actitud estudiantil. Moronta et al. (2019) aportan una perspectiva amplia sobre la relación entre motivación, ansiedad y autoestima. Su investigación revela que mayor motivación se asocia con menor ansiedad y mayor autoestima, al resaltar el papel de la estimulación en determinar el esfuerzo y la perseverancia, y cómo una autoestima elevada actúa a modo de elemento protector contra la ansiedad. Estas relaciones se ven influenciadas por factores como diferencias individuales y apoyo social.

Varias investigaciones señalan la influencia crucial de actitud, motivación y ansiedad matemáticas en el rendimiento académico y bienestar estudiantil. Acorde con Chiri et al. (2023), estos factores tienen un impacto significativo en el desempeño académico. Una actitud regular y una motivación media pueden afectar negativamente, mientras que una alta motivación intrínseca y extrínseca se relacionan con un mejor rendimiento. La ansiedad moderada también puede tener efectos negativos, como generar estrés y dificultades de concentración, lo que subraya la interrelación crítica entre estos aspectos. Bojorquez et al. (2021) apuntan que la ansiedad matemática puede disminuir la motivación para abordar tareas en esta área; relacionan la falta de motivación con la percepción de dificultad y ansiedad asociada. Pérez (2012) evidencia una correlación negativa importante entre ansiedad matemática y autoestima, al sugerir que mayores niveles de ansiedad se vinculan con menor autoestima, lo que también afecta la confianza para enseñar la materia. Por último, Alfaro y Valverde (2023) revelan una correlación inversa y notable entre ansiedad matemática y la actitud hacia la utilidad de la disciplina, cuando manifiestan que la ansiedad influye en la percepción de utilidad y motivación de la materia.

Método

Este estudio fue de corte cuantitativo descriptivo, ya que buscó especificar propiedades, características y rasgos importantes de un fenómeno; también fue correlacional, al evaluar el grado de asociación entre dos variables. Es decir, se examinó cada variable presuntamente relacionada y, luego, se analizó la correlación entre ellas (Hernández et al., 2016). La población de estudio estuvo constituida por la totalidad de estudiantes matriculados en el curso de precálculo, 457, en la Sede Metropolitana de la ULACIT, incluidos en el primer cuatrimestre de 2024. La muestra se conformó en las primeras semanas de dicho periodo, con el total de alumnos que completaron el instrumento en línea en el plazo establecido, así que resultaron 374 participantes.

Las variables utilizadas en la investigación fueron: género, área de estudio, ansiedad matemática, autoestima y motivación matemática, cuya definición conceptual y operativa se muestra en la tabla 1.

Tabla 1
Variables y definiciones operativas

Variable	Definición conceptual	Definición operativa
Género	Condición o identificación como femenino, masculino u otro.	La que indique el estudiante en el instrumento.
Área de estudio	Corresponde a ingeniería o a ciencias empresariales.	Según el estudiante indique en el formulario aplicado.
Ansiedad matemática	La ausencia de confort que alguien podría experimentar, cuando se le exige rendir en matemáticas.	Puntaje obtenido por el estudiante, mediante la aplicación de la Escala de ansiedad matemática de Fennema y Sherman (1976).
Autoestima	Consideración y valoración que posee una persona sobre sí misma (Rice, 2000, según se cita en Naranjo, 2007).	Puntaje obtenido por el estudiante, mediante la aplicación de la Escala de autoestima de autoestima de Rosenberg (1965).
Motivación matemática	Creencia sobre la utilidad de las matemáticas para la vida personal, el desarrollo laboral y profesional.	Puntaje obtenido por el discente estudiante, mediante la aplicación de la Escala de utilidad matemática de Fennema y Sherman (1976).

Nota: Elaboración propia (2024).

Como instrumentos de medición, se utilizaron las escalas de Fennema y Sherman (1976), para medir la ansiedad matemática y la actitud hacia la utilidad de la materia, validadas durante más de 40 años y alineadas con los objetivos de la investigación. Estos cuestionarios tipo Likert constan de 12 ítems cada uno, con 5 opciones de respuesta que van desde “totalmente de acuerdo” a “totalmente en desacuerdo”, incluyendo una opción neutra de “indeciso”. Dado que estas escalas presentan ítems redactados en sentido positivo y negativo, se decodificó el puntaje de algunos, para asegurar la consistencia a la hora de medir el nivel de motivación matemática. Con el propósito de evaluar la autoestima, se empleó la escala de Rosenberg (1965), usada por más de 50 años y adecuada para este estudio. Consta de 10 ítems tipo Likert, con 4 opciones de respuesta que van desde “muy de acuerdo” a “muy en desacuerdo”. Se recodificaron los últimos 5 ítems, para garantizar una medición coherente del nivel promedio de autoestima. La confiabilidad del instrumento se evaluó mediante el coeficiente “alfa de Cronbach”, considerando 0.8 como un valor mínimo adecuado (Cea, 1999). A modo de índice de “discriminación”, se utilizó, con base en Lozano y De la Fuente (2013), la correlación entre los puntos obtenidos en el ítem y los alcanzados en el instrumento, excluyendo lo correspondiente al ítem, con el fin de no incrementar de manera artificial el valor de la correlación entre ambas puntuaciones. Para validar el uso del análisis factorial, se aplicaron la “prueba de esfericidad de Bartlett” y el “índice de adecuación muestral” de Kaiser-Meyer y Olkin (KMO). La interpretación del coeficiente KMO siguió las recomendaciones establecidas por Kaiser (1974, según se cita en Frías-Navarro y Pascual, 2012). A saber:

0,9 < KMO ≤ 1,0: Excelente adecuación muestral

0,8 < KMO ≤ 0,9: Buena adecuación muestral

0,7 < KMO ≤ 0,8: Aceptable adecuación muestral

0,6 < KMO ≤ 0,7: Regular adecuación muestral

0,5 < KMO ≤ 0,6: Mala adecuación muestral

0,0 < KMO ≤ 0,5: Adecuación muestral inaceptable

Para el índice de Bartlett, se utilizó como criterio que cumpla con significancia menor al 5 %. Los índices de discriminación fueron evaluados de acuerdo con los parámetros establecidos en Lozano y De la Fuente (2013), que se muestran en la tabla 2:

Tabla 2
Índices de discriminación

Valores	Interpretación
Igual o mayor que 0,40	El ítem discrimina muy bien.
Entre 0,30 y 0,3	El ítem discrimina bien.
Entre 0,20 y 0,29	Ítem discrimina poco.
Entre 0,10 y 0,19	Ítem límite. Se debe mejorar.
Menor de 0,1	El ítem carece de utilidad para discriminar.

Nota: Lozano y De la Fuente (2013, p. 12).

Además, se efectuó un estudio de la unidimensionalidad, utilizando el análisis factorial, por ser esta la técnica más utilizada para esos propósitos (Jiménez y Montero, 2012). Se verificó el cumplimiento de al menos uno de los siguientes criterios, previo cálculo del índice KMO y de esfericidad de Bartlet:

•Helsie (1985, según se cita en Burga, 2006) establece que la estructura de un factor dominante tras el análisis de los autovalores es:

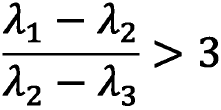
•Ello indica que se cumple la unidimensionalidad del instrumento.

•El primer factor explica el 40 % de la varianza (Carmines y Zeller, 1979, según se citan en Burga, 2006).

•El primer factor explica el 30 % de la varianza y el segundo menos del 10 % (Céspedes et al., 2011; Jiménez y Montero, 2012).

•Existencia de un codo después del primer autovalor en el gráfico de sedimentación (Céspedes et al., 2011).

Para el análisis de las hipótesis (de la 1 a la 6), se empleó la prueba t de Student, en casos de dos categorías, previa verificación de normalidad de datos y homogeneidad de varianzas. Cuando dicho resultado originó una diferencia estadísticamente significativa, se calculó el delta de Cohen para evaluar la magnitud del efecto, con interpretación basada en la escala de d de Cohen: alrededor de 0.20, diferencia pequeña; alrededor de 0.50, moderada; y 0.80 o más, grande (Morales, 2008; Ripoll, 2011). Para las hipótesis (de la 7 a la 9) sobre relaciones entre variables, se utilizó el coeficiente de correlación de Pearson, tras confirmar que el coeficiente no sea nulo. La interpretación de los coeficientes r de Pearson se basó en criterios establecidos por Aguayo (2004):

•Si | r | < 0,3 la asociación es débil.

•Si 0,30 < | r | < 0,70 la asociación es moderada.

•Si | r | > 0,70 la asociación es fuerte.

Resultados

Estadísticos descriptivos

La muestra obtenida corresponde a 374 estudiantes, los cuales se distribuyen de la siguiente manera (tablas 3 y 4):

Tabla 3
Distribución de la muestra por género

Género	Frecuencia	Porcentaje
Masculino	210	56.1 %
Femenino	164	43.9 %
Total	374	100 %

Nota: Elaboración propia (2024).

Tabla 4
Distribución de la muestra por área de estudio

Área	Frecuencia	Porcentaje
Ingeniería	334	89.3 %
Empresariales	40	10.7 %
Total	374	100 %

Nota: Elaboración propia (2024).

Resultado de la clasificación del nivel de ansiedad, motivación y autoestima matemáticas

La puntuación media en la escala de ansiedad matemática es 36, mientras que en este estudio se encuentra en 34.24, con una desviación estándar de 8.71, notablemente inferior al promedio (T(373) = 76.032, p < 0.05). Esto sugiere niveles de ansiedad considerablemente bajos en los estudiantes de la muestra. Por otro lado, la media en la escala de motivación matemática es 36, pero en este trabajo resultó en 44.77, con una desviación estándar de 8.56, marcadamente superior al promedio (T(373) = 101.070, p < 0.05). Esto indica niveles de motivación matemática ampliamente altos en los alumnos. En cuanto a la autoestima, la media es 29.90, con una desviación estándar de 5.18, bastante superior al promedio (T(373) = 111.443, p < 0.05). Esto insinúa niveles de autoestima muy altos en los participantes de la muestra.

El resultado sobre el nivel de ansiedad, motivación y autoestima matemáticas se clasificó en cinco categorías: “muy bajo”, “bajo”, “medio”, “alto” y “muy alto”. A continuación, se muestra esta clasificación para cada variable en estudio (tablas 5, 6 y 7).

Tabla 5
Clasificación del nivel de ansiedad matemática

Clasificación	Frecuencia	Porcentaje
Muy bajo	6	1.60 %
Bajo	83	22.19 %
Medio	201	53.74 %
Alto	76	20.32 %
Muy alto	8	2.14 %
Total	374	100 %

Nota: Elaboración propia (2024).

Tabla 6
Clasificación del nivel de motivación matemática

Clasificación	Frecuencia	Porcentaje
Muy bajo	0	0.00 %
Bajo	10	2.67 %
Medio	118	31.55 %
Alto	116	44.39 %
Muy alto	80	21.39 %
Total	374	100 %

Nota: Elaboración propia (2024).

Tabla 7
Clasificación del nivel de autoestima

Clasificación	Frecuencia	Porcentaje
Muy bajo	0	0.00 %
Bajo	13	3.48 %
Medio	139	37.17 %
Alto	176	47.06 %
Muy alto	46	12.30 %
Total	374	100 %

Nota: Elaboración propia (2024).

Resultados asociados al instrumento

Índice de discriminación de los ítems

La tabla 8 muestra los índices de discriminación de los ítems para cada una de las variables de este estudio.

Tabla 8
Índices de discriminación para cada variable

Ítem	Ansiedad matemática	Motivación matemática	Autoestima
1	0.512	0.680	0.471
2	0.332	0.634	0.480
3	0.462	0.644	0.574
4	0.418	0.641	0.639
5	0.620	0.643	0.601
6	0.471	0.639	0.434
7	0.681	0.603	0.660
8	0.681	0.658	0.355
9	0.491	0.724	0.703
10	0.615	0.567	0.428
11	0.563	0.441	--
12	0.733	0.487	--

Nota: Elaboración propia (2024).

De la tabla anterior, se establece que la mayoría de los ítems para cada una de las escalas discrimina bien, pues todos son mayores a 0.30, conforme al criterio dado por Lozano y De la Fuente (2013). Por ello, se conservan todos los ítems para los análisis a posteriori.

Confiabilidad del instrumento

Cea (1999) establece el valor adecuado de 0.80 como mínimo para establecer si una escala o instrumento muestra una adecuada confiabilidad. En la tabla 9, se muestra el alfa de Cronbach obtenido para las escalas de ansiedad matemática, motivación matemática y autoestima.

Tabla 9
Alfa de Cronbach para cada variable

	Ansiedad matemática	Motivación matemática	Autoestima
Alfa de Cronbach	0.865	0.895	0.834

Nota: Elaboración propia (2024).

De los resultados obtenidos, se tiene que las tres escalas son mayores a 0.80, por lo que cumplen una adecuada confiabilidad, siguiendo el criterio de Cea (1999).

Unidimensionalidad del instrumento

Para mostrar la razonabilidad de aplicar el análisis factorial, se procede a calcular el coeficiente KMO y de esfericidad de Bartlett. La tabla 10 muestra dichos resultados para la ansiedad matemática:

Tabla 10
KMO y esfericidad de Bartlett para la ansiedad matemática

Medida de adecuación muestral de KMO		0.890
Prueba de esfericidad de Bartlett	Chi-cuadrado aproximado	1662.413
	GI	66
	Significancia	0.000

Nota: Elaboración propia (2024).

De la tabla 10, se puede obtener que el KMO es de 0.890, por lo que indica una buena adecuación muestral, dado el criterio de Kaiser (1974, según se cita en Frías-Navarro y Pascual, 2012). A su vez, el valor de p < 0.001 en el índice de Bartlett también establece que es factible desarrollar un análisis factorial para estos datos. A continuación, se brindan los resultados del análisis factorial para la ansiedad matemática (tabla 11):

Tabla 11
Resultados del análisis factorial para la ansiedad matemática

Componente	Autovalores iniciales
	Total	% de varianza	% acumulado
1	4.985	41.541	41.541
2	1.190	9.916	51.457
3	1.062	8.849	60.305
4	0.847	7.060	67.366
5	0.725	6.040	73.406
6	0.706	5.880	79.286
7	0.583	4.860	84.146
8	0.532	4.433	88.579
9	0.417	3.473	92.052
10	0.385	3.210	95.261
11	0.303	2.523	97.785
12	0.266	2.215	100.000

Nota: Elaboración propia (2024).

Nótese que el criterio planteado por Carmines y Zeller (1979, según se cita en Burga, 2006) se cumple, pues el primer factor explica el 41.541 % de la varianza total, por lo que se evidencia la unidimensionalidad del instrumento.

Ahora, se procede a aplicar el análisis factorial. Para ello, se calcula el coeficiente KMO y de esfericidad de Bartlett. La tabla 12 muestra dichos resultados para la motivación matemática:

Tabla 12
KMO y esfericidad de Bartlett para la motivación matemática

Medida de adecuación muestral de KMO		0.907
Prueba de esfericidad de Bartlett	Chi-cuadrado aproximado	2215.375
	GI	66
	Significancia	0.000

Nota: Elaboración propia (2024).

De los resultados anteriores, se tiene que el KMO es de 0.907, por lo que indica una excelente adecuación muestral, debido al criterio de Kaiser (1974, según se cita en Frías-Navarro y Pascual, 2012). Ahora, el valor de p < 0.001 en el índice de Bartlett indica que es factible desarrollar un análisis factorial para los datos asociados a la motivación matemática. A continuación, se brindan los resultados del análisis factorial para dicha variable (tabla 13):

Tabla 13
Resultados del análisis factorial para la ansiedad matemática

Componente	Autovalores iniciales
	Total	% de varianza	% acumulado
1	5.729	47.743	47.743
2	1.481	12.343	60.086
3	0.809	6.740	66.826
4	0.766	6.554	73.380
5	0.656	5.468	78.848
6	0.511	4.260	83.108
7	0.442	3.681	86.790
8	0.385	3.206	89.996
9	0.342	2.850	92.846
10	0.318	2.647	95.493
11	0.287	2.388	97.881
12	0.254	2.119	100.000

Nota: Elaboración propia (2024).

El primer autovalor cumple con más del 40 % de la varianza, por lo que cumple la unidimensionalidad, de acuerdo con el criterio planteado por Carmines y Zeller (1979, según se citan en Burga, 2006). Seguidamente, se aplicó el análisis factorial para la variable autoestima, previo al cálculo del coeficiente KMO y de esfericidad de Bartlett. La tabla 14 muestra dichos resultados para esta variable:

Tabla 14
KMO y esfericidad de Bartlett para autoestima

Medida de adecuación muestral de KMO		0.855
Prueba de esfericidad de Bartlett	Chi-cuadrado aproximado	1353.639
	GI	45
	Significancia	0.000

Nota: Elaboración propia (2024).

Nótese que el KMO es de 0.855, por lo que señala una buena adecuación muestral, dado el criterio de Kaiser (1974, según se cita en Frías-Navarro y Pascual, 2012). Por otro lado, el valor de p < 0.001 en el índice de Bartlett también indica que es factible realizar un análisis factorial para estos datos. A continuación, se muestran los resultados del análisis factorial para la variable autoestima (tabla 15):

Tabla 15
Resultados del análisis factorial para autoestima

Componente	Autovalores iniciales
	Total	% de varianza	% acumulado
1	4.231	42.306	42.306
2	1.436	14.362	56.668
3	0.934	9.343	66.011
4	0.766	7.661	73.671
5	0.657	6.566	80.238
6	0.489	4.891	85.129
7	0.458	4.581	89.710
8	0.384	3.839	93.549
9	0.341	3.407	96.956
10	0.304	3.044	100.00

Nota: Elaboración propia (2024).

De lo anterior, se desprende que el primer factor explica el 41.541 % de la varianza total, por lo tanto, se cumple el criterio planteado por Carmines y Zeller (1979, según se citan en Burga, 2006). Así, se demuestra la unidimensionalidad del instrumento.

Contraste de hipótesis

•Hipótesis 1: Para contrastar esta hipótesis, se compararon las medias de ansiedad matemática entre hombres (M = 36.12, DE = 8.311) y mujeres (M = 31.85, DE = 8.464). Los resultados revelaron que existen diferencias estadísticamente notables entre ambos grupos (T(372) = 4.851, p < 0.05, d = 0.50). Por lo tanto, se rechaza la hipótesis nula y se concluye que sí existen diferencias marcadas en los niveles de ansiedad matemática, en función del género: los hombres presentan una ansiedad más pronunciada.

•Hipótesis 2: Para contrastar esta hipótesis, se compararon las medias de ansiedad matemática entre ingeniería y ciencias empresariales. Los resultados revelaron que no existen diferencias estadísticamente importantes entre ambos grupos (T(372) = 0.191, p > 0.05). Por lo tanto, se llega a la conclusión de que no hay diferencias estadísticamente relevantes en los niveles de ansiedad matemática, entre las distintas áreas de estudio.

•Hipótesis 3: Para examinar esta hipótesis, se llevó a cabo un análisis comparativo de las puntuaciones medias de autoestima entre hombres y mujeres. Los resultados obtenidos indicaron que no se observaron diferencias estadísticamente notables entre ambos grupos (T(372) = 1.291, p > 0.05). Por lo tanto, se llega a la conclusión de que no existen discrepancias estadísticamente sustanciales en los niveles de autoestima, en función del género.

•Hipótesis 4: Para explorar esta hipótesis, se hizo un análisis comparativo de las puntuaciones medias de autoestima entre estudiantes de ingeniería y ciencias empresariales. Los resultados revelaron que no se encontraron diferencias estadísticamente notables entre ambos grupos (T(372) = -0.640, p > 0.05). Por lo tanto, se concluye que no existen discrepancias estadísticamente relevantes en los niveles de autoestima, en relación con el área de estudio.

•Hipótesis 5: Para contrastar esta hipótesis, se ejecutó un análisis comparativo de las puntuaciones medias de la motivación matemática entre hombres (M = 43.74, DE = 8.724) y mujeres (M = 46.09, DE = 8.200). Los resultados obtenidos indicaron que no se observaron diferencias estadísticamente significativas entre ambos grupos (T(372) = -2.645, p < 0.05, d = 0.27). Por lo tanto, se rechaza la hipótesis nula, concluyendo que sí existen diferencias notables en los niveles de motivación matemática por género: las mujeres presentan una motivación más marcada.

•Hipótesis 6: Para explorar esta hipótesis, se realizó un análisis comparativo de las puntuaciones medias de motivación matemática entre estudiantes de ingeniería y ciencias empresariales. Los resultados revelaron que no se encontraron diferencias estadísticamente relevantes entre ambos grupos (T(372) = 1.877, p > 0.05). Por lo tanto, se concluye que no existen discrepancias estadísticamente significativas en los niveles de motivación, en cuanto al área de estudio.

•Hipótesis 7: Para contrastar las hipótesis, se procede a calcular la correlación de Pearson entre el promedio de la ansiedad de la matemática y la autoestima. Se determina que el valor de significancia obtenido es menor a 0.05, lo que indica que se debe rechazar la hipótesis nula. Por consiguiente, se llega a la conclusión de que existe evidencia de una correlación lineal entre ambas variables. En cuanto al coeficiente de Pearson, este se estima en -0.342. Dicho valor sugiere que la correlación entre la ansiedad matemática y la autoestima es inversa, notable y moderada.

•Hipótesis 8: Para examinar las hipótesis, se procede a calcular la correlación de Pearson entre la media de la ansiedad y la motivación matemáticas. Al realizar dicho contraste, se observa que el valor de significancia es menor a 0.05, lo que lleva al rechazo de la hipótesis nula. Por lo tanto, se concluye que existe una correlación lineal entre ambas variables. En cuanto al coeficiente de Pearson, este se estima en -0.230, lo cual sugiere una correlación inversa, relevante y de magnitud débil entre la ansiedad y la motivación matemáticas.

•Hipótesis 9: Para examinar las hipótesis, se procede a calcular la correlación de Pearson entre el promedio de la motivación matemática y la autoestima. Al realizar dicho contraste, se tiene un valor de significancia inferior a 0.05, lo que lleva al rechazo de la hipótesis nula y sugiere una correlación lineal entre ambas variables. En cuanto al coeficiente de Pearson, se sitúa en 0.188, lo cual indica una correlación positiva, marcada y de magnitud débil entre la motivación matemática y la autoestima.

Discusión y conclusiones

El análisis de los resultados revela que un 22.46 % de los estudiantes de la muestra exhibe un nivel promedio de ansiedad matemática alto. Este hallazgo se alinea con la investigación de Castro y Madrigal (2023), quienes encontraron que aproximadamente el 19 % de los alumnos matriculados en el bloque de matemática del tercer cuatrimestre de la ULACIT presentan un nivel alto en esta variable. Sin embargo, contrasta con varios estudios previos, como el realizado por Alfaro y Valverde (2023), en el cual más del 55 % de la muestra evidencia niveles altos de ansiedad matemática, y el de Castro (2023), en el que más del 80 % de los discentes se sitúan en el mismo nivel de clasificación de dicha variable. Estas discrepancias pueden atribuirse a diferencias en la metodología de estudio, las características de la muestra y las medidas utilizadas para evaluar la ansiedad matemática.

En relación con la variable de motivación matemática, se destaca que el 65.78 % de los estudiantes muestra niveles altos. Este hallazgo, aunque significativo, sugiere una tendencia a la alta motivación entre los alumnos en el contexto específico de este estudio. Sin embargo, resulta notable el contraste entre tal resultado y la investigación de Alfaro y Valverde (2023), en la cual se informó que el 93.34 % de los aprendices presentaba un nivel alto de motivación matemática. La diferencia sustancial plantea interrogantes trascendentales sobre los factores que podrían estar influyendo en los niveles de motivación matemática observados en distintas poblaciones estudiantiles.

En cuanto a la variable de autoestima, se observa que el 59.36 % de los estudiantes en la muestra exhiben niveles altos. Este resultado refleja una tendencia notable hacia una autoevaluación positiva entre los participantes del estudio. Coincidentemente, tal hallazgo está respaldado por la investigación de Moronta et al. (2019), quienes encontraron que aproximadamente la mitad de los alumnos en su muestra también fueron clasificados como poseedores de niveles altos de dicha variable. Este patrón consistente de autoestima elevada entre los estudiantes sugiere la existencia de un factor común o una influencia compartida que contribuye a este fenómeno. Es importante destacar que la autoestima es un aspecto fundamental del bienestar psicológico individual y puede influir significativamente tanto en su desempeño académico como en su desarrollo personal. Por lo tanto, comprender los determinantes y las implicaciones de los niveles de autoestima en el ambiente académico es crucial para diseñar intervenciones efectivas que promuevan el bienestar integral estudiantil.

El análisis de los datos reveló diferencias estadísticamente relevantes en el nivel promedio de ansiedad matemática por el género; la media de los hombres es mayor que la de las mujeres. Este resultado coincide con investigaciones previas realizadas por Nadide (2020) y Suren y Kandemir (2020), quienes encontraron que los hombres experimentaban una mayor ansiedad en actividades relacionadas con la disciplina matemática. No obstante, otros estudios como los de Delgado-Monge et al. (2020), Bojorquez et al. (2021) y Alfaro y Valverde (2023) presentan resultados contradictorios, al establecer que las mujeres son las que muestran niveles más altos de ansiedad. Además, indagaciones más recientes como las de Castro (2023) y Castro y Madrigal (2023) sugieren que no hay diferencias importantes en la ansiedad matemática, en cuanto al género. Un aspecto importante para considerar es la influencia del sesgo de respuesta en este tipo de estudios. Pérez (2012) señala que las mujeres tienden a contestar con mayor honestidad a los instrumentos de medición en torno a sus experiencias, lo que podría influir en los resultados. Por lo tanto, la discrepancia en los hallazgos entre trabajos podría atribuirse, en parte, a las diferencias en la sinceridad de las respuestas de hombres y mujeres, ante las preguntas relacionadas con la ansiedad matemática.

Por otro lado, en lo que respecta a la motivación matemática, se observa una diferencia estadísticamente importante entre hombres y mujeres: las mujeres muestran una mayor motivación. Este descubrimiento está respaldado por diversas investigaciones, entre las cuales se encuentran los estudios de Suren y Kandemir (2020) u Ortiz-Padilla et al. (2020). No obstante, tales resultados discrepan de las indagaciones de González-Vázquez (2019) y Alfaro y Valverde (2023), en las cuales se encontró que los hombres exhiben una actitud más favorable hacia la asignatura de matemáticas. Es importante destacar que esas diferencias pueden atribuirse a variaciones en las muestras estudiadas, en la metodología utilizada o en el entorno particular de cada investigación.

En cuanto a la autoestima, no se observaron distinciones notables en función del género. No obstante, este resultado contradice los de investigaciones previas, como las de Moronta et al. (2019), González-Vázquez (2019) y Gezu et al. (2020, según se citan en Cirilo, 2021), las cuales sugieren la existencia de diferencias de autoestima en función del género. Sin embargo, es importante destacar que no se ha establecido un patrón definido que determine cuál género posee una autoestima superior en relación con el otro.

Para el área de estudio, no se encontraron diferencias estadísticamente relevantes en el nivel promedio de ansiedad, motivación matemática y autoestima. En el caso específico de la ansiedad matemática, este resultado contrasta con la investigación de Castro y Madrigal (2023), quienes encontraron que los estudiantes de ciencias empresariales exhibían niveles de ansiedad matemática más altos en comparación con los de ingeniería. Pero, en lo que respecta a la motivación y autoestima, aún no se han realizado trabajos específicos sobre estas variables, en relación con el área de estudio, en ámbitos universitarios regionales. Por lo tanto, no es posible establecer ninguna comparación entre los resultados obtenidos y otros previos.

Seguidamente, se llevó a cabo un análisis de la relación entre variables, comenzando con la ansiedad matemática y la autoestima. Los hallazgos revelaron un enlace significativo, el cual fue inverso y moderado. En otras palabras, se observa que, a medida que disminuye la ansiedad matemática, tiende a aumentar la autoestima. Este resultado coincide con varios estudios previos, incluyendo los efectuados por Pérez (2012), Moronta et al. (2019), Cirilo (2021) y Chiri et al. (2023), quienes también encontraron una asociación similar entre las dos variables mencionadas, en ambientes universitarios.

Al examinar el vínculo entre la ansiedad y la motivación matemáticas, se evidenció una correlación importante, la cual se caracterizó por ser inversa y débil. Específicamente, se observó que, a medida que los niveles de ansiedad matemática disminuyen, la motivación hacia la asignatura aumenta de manera notable. Este descubrimiento respalda indagaciones anteriores ejecutadas por Pérez (2012), Villar et al. (2022), Alfaro y Valverde (2023) y Chiri et al. (2023), quienes encontraron resultados similares, al explorar el ligamen entre estos dos constructos en escenarios educativos parecidos.

Finalmente, se llevó a cabo el análisis del nexo entre la motivación matemática y la autoestima: reveló una correlación notable, positiva y de naturaleza débil. En términos simples, se encontró que, según aumenta la motivación hacia las matemáticas, también lo hace la autoestima. Esto coincide con las investigaciones de Moronta et al. (2019) y Cirilo et al. (2021), quienes igual encontraron una relación positiva entre estos dos aspectos, en ambientes similares.