Revista Ensayos Pedagógigos Edición Especial, 2016 (ISSN 1659-0104) URL: http://www.revistas.una.ac.cr/ensayospedagogicos De la página 19 a la 35 del documento escrito

---

Las redes sociales y su modelado matemático

Social Networks and their Mathematical Modeling

Juan Carlos Ortega Guerrero1

Resumen

Las tecnologías de la información y comunicación (TIC) han venido a cambiar el potencial de las redes sociales. Su diversidad, alcance y características resultan impactantes y su análisis matemático es importante para comprenderlas. En este capítulo se revisan los conceptos básicos de las redes, veremos cómo se generan las redes complejas y sus características principales; en especial se analizan las redes de mundo pequeño y su uso para modelar las redes sociales, finalmente se enuncian algunas limitaciones que tienen estos modelos matemáticos en la representación de la realidad social.

Palabras clave: redes sociales, análisis de redes, modelos matemáticos, teoría de grafos, internet.

Abstract

The information and communication technologies (ICT) have come to change the potential of social networks. Their diversity, scope and characteristics are creating a great impact on society, and their mathematical analysis is important to understand that. This chapter describes the basic concepts of networks; we will see how complex networks and their main characteristics are generated, especially small-world networks and their use to model social networks will be analyzed. Finally, some limitations with these mathematical models in the representation of social reality are described.

Keywords: social networks, network analysis, mathematical models, graph theory, Internet

Introducción

Actualmente es común escuchar acerca de las redes sociales y su importancia para establecer comunicación entre amistades, relacionar a grupos de investigación o hacer negocios. Aunque dicho concepto no es nuevo, su análisis se ve potenciado al estar ubicadas en internet; el concepto de estas redes se ha resignificado con la aparición de las TIC (Molina, 2011). Tenemos muchos tipos de redes sociales: Facebook, Twitter, Pinterest, Google+, LinkedIn, MySpace, Hi5 además de multitud de sistemas que, aunque no fueron pensados como redes, han transitado hacia ese modelo: YouTube, Reddit, Instagram, Foursquare y muchas otras.

Las consecuencias de estar conectado en redes sociales pueden resultar sorprendentes e inesperadas: por ejemplo, si una persona tiene 100 amigos y amigas en Facebook, y si cada quien de este grupo tiene a su vez un promedio de 100 amistades (suposición muy conservadora), podría estar conectada en dos pasos con 10,000 personas. Por otro lado, estamos incluidos sin saberlo en otras redes; por ejemplo, si compramos un libro para leerlo en un dispositivo Kindle conoceremos no solo quién más lo compró sino qué otros libros adquirió e, inclusive, cuáles párrafos le resultaron interesantes.

Todas estas redes se pueden describir través de modelos matemáticos de redes complejas. Conocer cómo se estructura una red compleja y qué dinámica se puede generar en ella resulta importante para comprender su funcionamiento, prevenir los riesgos que tiene y mejorar su uso.

¿Qué son las redes?

Todos conocemos objetos a los que denominamos red: las redes de pesca, las telarañas, la red de caminos, las redes de computadoras, la red de agua potable, etcétera. Todas las anteriores nos refieren a la idea de objetos (nudos, poblaciones, computadoras, casas, personas) conectados entre ellos (el hilo de la red o de la telaraña, los caminos, cableado, tubos que conducen agua, relaciones de parentesco). Desde un punto de vista formal una red, o grafo en términos matemáticos, es un conjunto de objetos denominados nodos con conexiones entre ellos denominadas aristas como puede verse en la Figura 1.

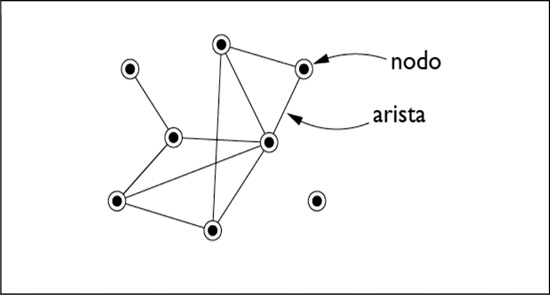
Figura 1.
Red con ocho nodos y diez aristas. Adaptado de Newman (2003, p. 169).

Atendiendo a su topología, podemos clasificar las redes en dos grandes tipos: las regulares o monótonas y las complejas. Las redes regulares (como las redes de pesca, algunas redes de computadoras sencillas y las telarañas) no presentan dificultades especiales al analizarlas ya que generalmente cada uno de sus nodos es igual a los otros, las aristas son iguales entre sí. Dentro de este tipo de redes encontramos las lineales, las de anillo, las de estrella, las de árbol y las de malla. Como puede verse en la Figura 2, en cada una de estas redes las aristas son iguales y cada nodo tiene el mismo número de vecinos (exceptuando los nodos de los extremos o de las orillas) (Dorogovtsev y Mendes, 2003; Newman, 2003).

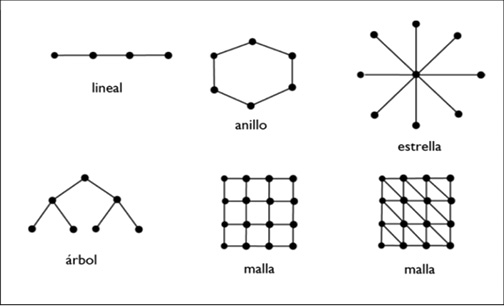
Figura 2.
Redes monótonas. Elaboración propia.

Las redes complejas reciben este nombre debido a que las características de los nodos, las aristas y la forma en que están conectadas son diversas. Como puede verse en la Figura 3, podemos tener diferentes tipos de nodos que pueden representar, por ejemplo, tipos de computadoras. También podemos ver diversos tipos de aristas que pueden representar, por ejemplo, la calidad del cableado que conecta las computadoras o el ancho de banda que manejan; en el gráfico (d) de la misma Figura 3 vemos aristas dirigidas que pueden indicar, por ejemplo, cuál computadora manda información a otra.

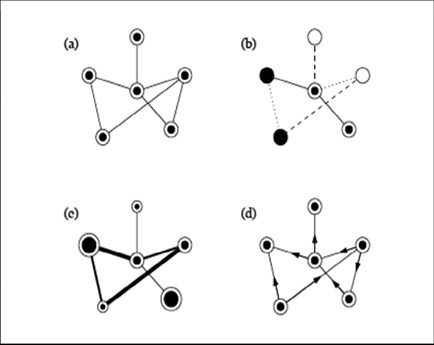
Figura 3.
Conexiones en redes no monótonas. Adaptado de Newman (2003, p. 4).

Redes complejas

Las redes complejas se vuelven importantes e interesantes cuando están integradas por una gran cantidad de nodos y aristas. Existen una gran cantidad de fenómenos naturales y artificiales que pueden ser comprendidos por medio de la estructura de redes complejas, por ejemplo, la estructura social puede representarse como una red de personas relacionadas con sus familiares o amigos. Otro ejemplo de red compleja es el cerebro, ya que está formado por neuronas de las cuales existen aproximadamente 100 000 millones, de más de 300 tipos diferentes que se conectan en promedio a través de más de 7 000 conexiones cada una (Bear et al., 2001). También el lenguaje puede ser estudiado, si se le piensa como una red de palabras conectadas por reglas sintácticas (Solé et al., 2010).

En 1959 dos matemáticos húngaros (Erdős y Rényi, 1959) propusieron estudiar las redes complejas con un modelo matemático en el que el número de nodos y aristas crecía de manera aleatoria. Este modelo predecía que los nodos tendrían aproximadamente el mismo número de aristas en una distribución de Poisson. Sin embargo, estas predicciones se contradijeron con evidencia empírica lograda a través de sistemas de cómputo cada vez más accesibles. En 1998, al estudiar la estructura de la Word Wide Web se encontró que más del 80 por ciento de las páginas eran apuntadas por menos de cuatro ligas y que solo el 0.01 por ciento de las páginas tenía más de mil. Se propuso, entonces, el modelo denominado de escala libre, que respondía a este fenómeno además de explicar mejor la estructura de otras redes complejas (Barábasi y Bonabeau, 2003).

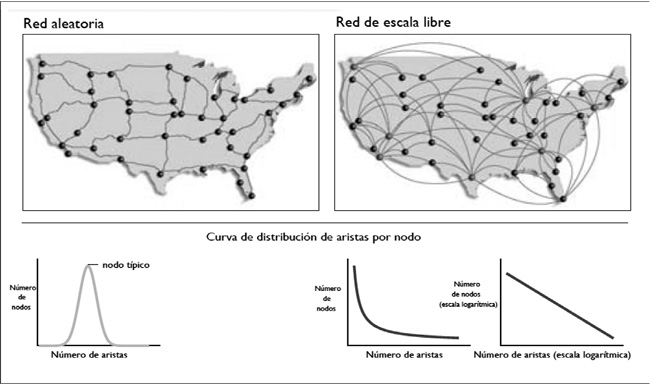
Figura 4.
Redes aleatoria y de escala libre.
Adaptación de Barábasi y Bonabeau (2003, p. 64).

En la Figura 4, se muestra a la izquierda la red de autopistas (de los Estados Unidos) como modelo de una red aleatoria. Cada ciudad se comunica con un promedio de cuatro carreteras. A la derecha se muestra la red de enlaces aéreos t se marcan en rojo los pocos aeropuertos que tienen un gran número de conexiones por lo que se dice que están fuera de escala. Barábasi y Bonabeau (2003) encontraron que muchas redes podían explicarse con el modelo de escala libre, por ejemplo:

• La red de metabolismos celulares, en la que los nodos son las moléculas usadas para procesar los alimentos y las aristas son su participación en las reacciones bioquímicas.
• La red de actores de películas, en la que los nodos son los actores y las aristas son las películas en las que actúan.
• El Internet físico, con los routers como nodos y las conexiones físicas (fibra óptica, cableado de cobre y conexiones inalámbricas) como aristas.
• Las colaboraciones entre personal investigador, en donde los nodos son el personal investigador y las aristas son los artículos de su coautoría (Reynolds, 1999).
• Las relaciones sexuales sentimentales, con la gente como nodos y sus parejas como aristas (Eames y Keeling, 2002).
• La WWW, con las páginas como nodos y las ligas (links) como aristas.
• Las citas entre artículos científicos, con artículos como nodos y las citas como aristas (Dorogovtsev y Mendes, 2003).

Algunos conceptos básicos

Debido a la gran cantidad de nodos y aristas que tienen las redes complejas, ha sido necesario estudiarlas con herramientas estadísticas que no toman en cuenta los componentes individuales de las redes (los nodos y aristas) y en cambio se enfocan en medir las características globales de estas mismas. En este sentido, se ha propuesto (Barábasi y Bonabeau, 2003; Dorogovtsev y Mendes, 2003; Newman, 2003) medir muchas características de una red compleja; pero en especial se recurre a tres parámetros para determinar sus características topológicas: la distancia promedio entre nodos (average path length), el coeficiente de agrupamiento (clustering coefficient) y la distribución de grado (degree distribution), veamos su definición y significado.

Distancia promedio entre nodos (L). En una red la distancia dij entre dos nodos, denominados i y j, se define como el número de aristas que hay que recorrer para llegar de uno al otro pasando por el menor número de aristas (a esto se le denomina el “camino más corto posible”, aunque no hay ninguna medida de la longitud de las aristas). La distancia promedio entre nodos L se define, entonces, como el promedio de las distancias entre todos los nodos. En una red de amistades el parámetro L será el número promedio de personas que hay entre dos amistades de la red.

Diámetro (D). De lo anterior se deriva otro concepto conocido como diámetro D de la red, que es la distancia máxima (medida por el número de aristas) entre cualquier par de nodos.

Coeficiente de agrupamiento (C). Para estimar qué tan interconectada está una red utilizamos el coeficiente de agrupamiento. Se define que un nodo es vecino de otro cuando hay un solo vértice entre ellos, es decir, están conectados directamente, sin intermediarios. El coeficiente de agrupamiento C se refiere a la porción de nodos de la red cuyos vecinos son a la vez vecinos de otros nodos. Supongamos que un nodo i tiene ki vértices que lo conectan con ki nodos, el número de nodos que pueden existir entre sus vecinos es ki (ki-1)/2, en caso de que estos vértices existan tendremos una red en la que todos sus nodos están interconectados. Por ejemplo, si tenemos un nodo con cuatro vecinos habrá máximo de seis vértices entre esos cuatro nodos (4 x 3 / 2). En el caso de una red de amistades esto significa que todas mis amistades son amigos o amigas entre sí. El coeficiente de agrupamiento Ci de un nodo i es la proporción de los vértices que realmente existen entre los vecinos del vértice. El coeficiente de agrupamiento C de la red es entonces el promedio de los coeficientes de agrupamiento de cada vértice.

Distribución de grado (G). El grado de un nodo es el número de aristas que tiene. La distribución de grado de una red es la distribución de probabilidad de los grados de sus nodos. Esta característica, que es la más sencilla de evaluar en las redes, es la de mayor importancia en el estudio de las redes complejas. En una red simple la mayoría de los nodos tienen el mismo grado; en una red aleatoria la distribución de grado sigue una distribución normal en la que encontramos una moda y una media; por el contrario en las redes de escala libre encontraremos pocos nodos con grado alto y muchos nodos con un grado pequeño, así mismo la distribución de los grados disminuye exponencialmente (ver Figura 4).

Redes de mundo pequeño

Todos conocemos anécdotas de viajeros que estando lejos de sus lugares de origen se encuentran con personas que conocen a sus amigos, “¡qué pequeño es el mundo!” se suele decir. En 1967 Stanley Milgram publicó el resultado de una investigación (Milgram, 1967) en la que buscaba conocer qué tan relacionados estaban los habitantes en los Estados Unidos. Para ello, mandó varios cientos de cartas a habitantes de Nebraska, pidiéndoles que las reenviaran a alguna persona conocida que pudiera hacerlas llegar a un destinatario o destinataria final que estaba en la ciudad de Boston. Con el fin de conocer el recorrido de las cartas, pedía a los sujetos participantes que anotaran sus datos en una tarjeta antes de darla a la siguiente persona participante. Lo que encontró Milgram es que las cartas pasaban en promedio por seis individuos antes de llegar al destinatario final. Esto dio base al concepto popular de los seis grados de separación entre cualquier persona y detonó el estudio formal de lo que solemos llamar redes de mundo pequeño. El problema de mundo pequeño puede plantearse de la siguiente manera: tomando a dos personas en el mundo ¿cuál es la probabilidad de que se conozcan?, ahora bien, si no se conocen, ¿a cuántos conocidos intermedios tienen que recurrir para entrar en contacto?

Más allá de cuestiones anecdóticas, el problema de mundo pequeño es importante para quienes se dedican a la historia, política, biología y especialistas en comunicación entre muchas otras profesiones. Para representar matemáticamente este fenómeno, Watts y Strogatz (1998) propusieron un modelo que mezcla una red monótona en forma de anillo (ver Figura 5 a) a la cual se aplica un proceso de reconexión de vértices de manera aleatoria, determinado por el valor de p que puede ir de 0 a 1 sin alterar el número de nodos y vértices. El proceso es el siguiente:

• Se asigna un valor p que es la probabilidad de seleccionar y reconectar una arista; p toma valores de 0 a 1, es decir puede valer 0, 0.1,..., ...,0.9, 1.
• Se recorren cada una de las aristas y se le selecciona con probabilidad p, por ejemplo si p=0.5 aproximadamente la mitad de las aristas se reconectará.
• Si la arista se seleccionó, se elige el nuevo nodo destino de forma aleatoria.

Este proceso introduce aristas que conectan nodos inicialmente distantes creando “atajos” en la red.

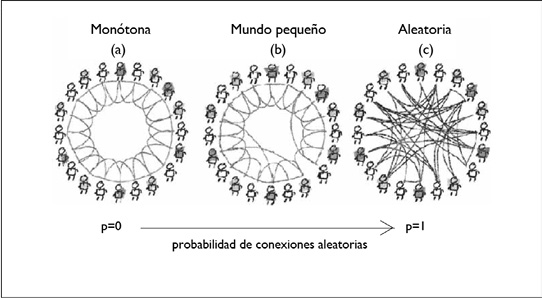
Figura 5.
Redes de mundo pequeño.

Adaptado de Wang y Chen (2003); Watts y Strogatz (1998).

En la Figura 5 se muestran tres redes de amistades, la primera (a) es monótona y regular, cada persona tiene cuatro amistades directas. La red está compuesta de individuos muy aislados, ya que la distancia promedio entre dos individuos es grande, tienen muchos grados de separación. La red (b) es una red de mundo pequeño, aunque cada persona sigue teniendo en promedio cuatro amistades hay una menor distancia a las más lejanas. Los individuos aún están aislados, pero el grado de separación promedio es pequeño debido a los atajos creados. La tercera red (c) es aleatoria ya que el 100 por ciento de las aristas se reconectaron debido a que la probabilidad de ser seleccionada era 1, cada individuo aún tiene cuatro amistades en promedio, pero están dispersas: pocos tienen amistades en común, pero el grado de separación es pequeño.

La estructura de las redes de mundo pequeño está definida por la distancia promedio entre nodos L, que es una propiedad global, y por el coeficiente de agrupamiento C, que es una propiedad local. Cuando escogemos una probabilidad p de reconexión de aristas pequeño (aunque depende del número de nodos el valor de p deberá estar entre 0.001 y 0.1), el resultado es una combinación de L y C que nos da una red de mundo pequeño con creación de atajos más o menos espaciados que evitan que la red corra el peligro de fraccionarse en secciones no conectadas.

Mediciones de diversas redes reales (Wang y Chen, 2003) han encontrado que los parámetros de L y C coinciden con los valores previstos para ser modeladas como redes de mundo pequeño, como puede verse en la Tabla 1 en la que los coeficientes de agrupamiento C y la distancia promedio L entre nodos son pequeños.

Tabla 1
Características de algunas redes tecnológicas y sociales

Nota: Adaptado de Wang y Chen (2003).

Las redes sociales tienen características diferentes a las redes naturales (redes de presa-depredador, redes neuronales, red de interacción de proteínas, entre otras) o a las propiamente tecnológicas (como las redes de carreteras o la red del tendido eléctrico).

Redes sociales y su representación como redes de mundo pequeño

Aunque podemos incluir en el análisis de redes sociales el estudio de diversos temas (construcción de sintaxis en diversos idiomas, redes de cómputo, etc.), generalmente se les denomina así a las que tienen personas u organizaciones sociales como nodos.

Podemos entonces definir una red social como una estructura social compuesta por individuos u organizaciones denominados nodos, los cuales están conectados por uno o más tipos de interdependencia o relaciones como amistad, parentesco, intereses comunes, intercambios financieros, antipatía, relaciones sexuales, creencias, conocimientos o prestigio (Kadushin, 2011; Social Network Analysis, 2011).

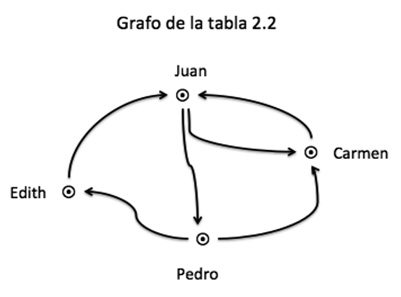
Desde el punto de vista de la investigación sociológica, los datos que se analizan en redes sociales difieren de los que se usan en otro tipo de estudios. En un estudio social es común tomar en cuenta atributos sobre los sujetos como la edad, el género y la escolaridad, con los cuales se hacen comparaciones, se definen grupos o se crean taxonomías; por otra parte, los atributos que se analizan en estudios de redes sociales son las relaciones que existen entre los sujetos. En la Tabla 2 pueden verse dos formas de representar la información de redes: matrices y grafos. Si observamos los renglones de la matriz 2.2 podemos ver quién dice conocer a quién; si analizamos las columnas podemos observar quién ha sido seleccionado como conocido por quién, la misma información se ve en el grafo.

Otra diferencia entre los estudios sociales (en los cuales es común aplicar encuestas) y los estudios de redes sociales es la técnica para la selección de los sujetos de estudio. En los primeros, los sujetos son seleccionados de manera aleatoria buscando que las muestras sean representativas de la población en estudio; en los segundos, puesto que los atributos a medir son las relaciones entre los sujetos, se tendrán que incluir a los nodos de la red, es decir, no es posible seleccionar muestras, tendrán que incluirse todos los sujetos relacionados.

Tabla 2
Información para análisis sociales generales y análisis de redes

Nota: Adaptado de Hanneman y Riddle (2005, pp. 2-3).

Cuando recabamos información acerca de las relaciones entre personas, tenemos que seleccionar qué tipo de dato queremos medir y representar como arista o relación entre los nodos. Se clasifican los objetos que representan las aristas en dos tipos: material e informacional. En el primer tipo incluimos objetos materiales que se mueve por las aristas y pueden ser ubicadas en algún momento en uno u otro de los nodos, por ejemplo, intercambios económicos, automóviles que se mueven entre ciudades, documentos que cambian de dueño. Los objetos informacionales son aquellos que no se conservan o pueden estar en dos lugares a la vez, como pueden ser intercambio de información, tipo de relación entre personas, dependencia entre empresas.

Los objetos representados por las aristas también tienen diferentes escalas de medida: binarias, nominales, ordinales grupales, ordinales completas e intervalos. Las medidas binarias son las más comúnmente utilizadas, suelen representar presencia o ausencia de una relación y se codifican como si o no, uno o cero, presencia o ausencia de una arista. Las medidas nominales incluyen grados de la relación, por ejemplo, dos personas pueden tener una relación de amistad, ser novios, ser compañeros de trabajo o no conocerse. En el proceso de análisis es común dividir una medida nominal en varias medidas binarias, una por cada clase de relación.

Por medio de las medidas ordinales grupales se representa la fuerza o intensidad de una relación (del tipo me gusta, me disgusta, me es indiferente) o la frecuencia de los contactos (por ejemplo, diario, semanal, mensual). Algunas veces es posible asignar grados a cada una de las relaciones por medio de medidas ordinales completas, por ejemplo, cuando se pide ordenar de 1 a n el grado de cercanía con un grupo de n personas conocidas. Por último, las medidas por intervalos nos permiten estimar la distancia que hay entre una medida y otra, esto es que la diferencia entre una arista que vale 1 y otra que vale 2 es la misma entre otras dos que miden 12 y 13 respectivamente, por ejemplo, cuando etiquetamos las aristas con los importes monetarios, redondeados a miles, transferidos entre personas.

A pesar de que las medidas con menos información son las binarias, en la práctica encontramos que la mayoría de los estudios de redes se llevan a cabo con grafos de aristas dirigidas y binarias (ver grafo de la Tabla 2) (Hanneman y Riddle, 2005).

Limitaciones de los modelos matemáticos de redes sociales

A pesar de las diferentes propuestas para formular modelos matemáticos de redes sociales y en especial que las redes de mundo pequeño han sido muy útiles para este fin, se siguen teniendo problemas para representarlas adecuadamente. Duncan Watts (1998) agrupa dichos problemas en teóricos y empíricos como veremos a continuación. Dentro de los problemas teóricos a considerar tenemos el problema de la escala, ya que al incrementarse el tamaño de las redes se dificulta su análisis de manera exponencial; ni usando las más poderosas computadoras se puede tener una solución exacta, solo pueden ser resueltos de manera aproximada. Otro problema teórico es la heterogeneidad al interior de las redes, que se debe a que las redes sociales presentan características locales, de tal modo que el análisis de una parte de ellas no puede predecir el comportamiento en otras partes. Esto nos lleva al problema de que las redes sociales no se comportan como una red continua, sino más bien como una familia de redes con propiedades estructurales (distancia promedio entre nodos, coeficiente de agrupación y distribución de grado), que varían en sus diferentes secciones y que presentan zonas de transición entre ellas. Encontramos dificultades para representar relaciones de poder y centralismo, grupos de amigos y subgrupos dentro de los grupos (Hanneman y Riddle, 2005). Por otra parte, la métrica con la cual se miden las aristas en las relaciones sociales tiene al menos dos aspectos difíciles de definir: la distancia que hay entre dos nodos y qué tan fuerte es esa relación, pues las “distancias” no responden a una métrica espacial y la fuerza en las relaciones resulta muy subjetiva (recordemos, por ejemplo, la gran cantidad de solicitudes de amistad que recibimos de personas conocidas que rechazamos por no considerarlas suficientemente cercanas).

En lo que concierne a los problemas de tipo empírico, nos encontramos con la dificultad de obtener información suficientemente detallada de grandes redes. A pesar de tener recursos como internet no está disponible toda la información necesaria para el análisis, debido a su inexistencia o a restricciones impuestas por seguridad en las mismas redes sociales. Incluso, señala Watts (1999), hay problemas para determinar el número promedio de “amigos” (parámetro básico de una red social) ya que las personas tienden a subestimar el número de sus conocidos, en especial, si no damos un significado concreto a la palabra “amigo”.

A manera de cierre

Se han descrito los conceptos básicos que definen una red y algunas de las propuestas para modelar matemáticamente las redes sociales, así como sus limitaciones para representar adecuadamente redes reales. Como apunta Nicola Perra (2015), las denominadas redes sociales en línea (Facebook, Twitter, etc.) son cada vez más importantes en nuestras vidas. Su estudio puede darnos información de cómo interactúan e intercambian información las personas, pero más importante que esto, quizá es posible entender la forma en que la sociedad se desarrolla para generar una mejor infraestructura de comunicación que ayude a resolver algunos problemas sociales. Para lograrlo, es necesario seguir desarrollando los modelos matemáticos que permitan analizar cantidades ingentes de información que tenemos a través de internet.

A finales del siglo XX la idea de que las relaciones sociales consisten de redes a las que nos unimos y a través de las cuales interactuamos generó una serie de metáforas, conceptos, teorías y representaciones matemáticas a través de las cuales se intentó comprenderlas; parecía que el campo de investigación pasaba de la sociología (cfr. el desarrollo de “sociogramas” del psiquiatra Jacob Moreno en 1953) a las ciencias duras como la física y las matemáticas. Sin embargo, pronto se vieron las limitaciones de analizar el fenómeno de las redes sociales exclusivamente desde uno u otro punto de vista. Por otra parte, como hace notar Kadushin (2011, p. 200), “...las redes [sociales] se insertan en un sistema de instituciones sociales que a su vez están embebidas en un sistema de redes sociales y esto genera un mecanismo de retroalimentación entre las redes y las instituciones.” En conclusión, para mejorar nuestra comprensión sobre las redes sociales será necesario tomar en cuenta los dos enfoques mencionados (sociológico y físico-matemático) así como la doble reflexión entre redes e instituciones.

Referencias

Barábasi, A.-L., y Bonabeau, E. (Mayo, 2003). Scale Free Networks. Scientific American, 60-69.

Bear, M. F., Connors, B. W., y A., P. M. (2001). Neuroscience. Exploring the Brain. Baltimor: Lippincott Williams & Wilkins.

Dorogovtsev, S. N., y Mendes, F. F. F. (2003). Evolution of Networks. From biological nets to the Internet and WWW. Oxford: Oxford Press.

Eames, K. T., y Keeling, M. J. (2002). Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proceedings of the National Academy of Sciences of the United States of America, 99(20), 13330-13335.

Erdős, P., y Rényi, A. (1959). On Random Graphs. Publicationes Mathematicae, 6, 290-297.

Hanneman, R. A., y Riddle, M. (2005). Introduction to Social Networks. Recuperado de http://www.analytictech.com/networks.pdf

Kadushin, C. (2011). Understanding Social Networks: Theories, Concepts and Findings. New York: Oxford University Press.

Milgram, S. (1967). The Small-World problem. Psychology Today, 1 (1), 61-67.

Moreno, Jacob L. (1953). Who shall survive? Foundations of sociometry, group psychoterapy and sociodrama. New York: Beacon House. [Originalmente publicado como Moreno, Jacob L. (1934). Nervous and Mental Disease Monograph, vol. 58. Washington, D.C. ]

Newman, M. E. J. (2003). The Structure and Function of Complex Network. SIAM REVIEW, 45(2), 167-256.

Perra, N. (2015). Modeling and Studying Online Social Networks. Recuperado de http://www.nicolaperra.com/modeling-and-studying-online-social-networks.html

Reynolds, P. (1999). The Oracle of Bacon. Recuperado de https://oracleofbacon.orghttps://oracleofbacon.org/

Social Network Analysis. (2011). Theory and Applications. (pp. 116). Recuperado de http://train.ed.psu.edu/WFED-543/SocNet_TheoryApp.pdfhttp://train.ed.psu.edu/WFED-543/SocNet_TheoryApp.pdf

Solé, R., Corominas, B., Valverde, S., y Steels, L. (2010). Language Networks: Their structure, function and evolution. Complexity, 15(6), 20-26.

Wang, X. F., y Chen, G. (2003). Complex Networks: Small-World, Acale-Free and Beyond. IEEE Circuits and Systems Magazine, 2003 (1), 6-21.

Watts, D. J. (1999). Small worlds: the dynamics of networks between order and randomness. New Jersey: Princeton University Press.

Watts, D. J., y Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393, 440-442.

---