Morfometría de la subcuenca hidrográfica del río Páez, Cartago, Costa Rica

Morphometry of the Páez River hydrographic sub-basin, Cartago, Costa Rica.

Pablo Ramírez-Granados1

Universidad Nacional, Costa Rica, Costa Rica

Kevin Alfaro-Jiménez2

Universidad Nacional, Costa Rica, Costa Rica

María Álvarez-Jiménez3

Universidad Nacional, Costa Rica, Costa Rica

Ligia Dina Solís-Torres4

Universidad Nacional, Costa Rica, Costa Rica

José Castro Solís5

Universidad Nacional, Costa Rica, Costa Rica

Resumen

Los estudios de morfometría brindan información sobre el funcionamiento hidrológico en una cuenca. El objetivo del estudio fue determinar parámetros morfométricos en la subcuenca del rio Páez, Cartago necesarias para planificación de las actividades de la cuenca y para un apropiado manejo. La construcción de la morfometría se basó en las curvas de nivel del Gran Área Metropolitana, escala 1:10000, y utilizando los Sistemas de Información Geográfica, se realizó la digitalización de las curvas de nivel, los drenajes y el parteaguas. Resultado del análisis morfométrico, se obtiene un área de 28,34 km2 y un perímetro de 47,4270 km. Está compuesta por 22 microcuencas, un factor de forma de 0,1171indicando una subcuenca alargada. Un coeficiente de compacidad de 2,4942, indicando que es una cuenca elongada. Muestra una curva hipsométrica de tipo cóncava, donde el pico de la distribución altimétrica corresponde con las altitudes entre los 3315 m y los 980 m. El parámetro pendiente con un valor de 29,3% de pendiente promedio. Es evidente la función que cumple la subcuenca para el desarrollo de las actividades productivas y para el abastecimiento de agua potable en algunos sitios Cartago.

Palabras clave: subcuenta Páez, morfometría.

Abstract

Morphometric studies provide information on the hydrological functioning in a basin. The objective of the present study was to determine morphometric parameters in the sub-basin of the Páez River, located in the province of Cartago, Costa Rica, necessary for land use planning within the basin and its proper management. Morphometric construction was based on the 1:10,000 scale contour lines available for the Gran Area Metropolitana (translated as the Greater Metropolitan Area) and geographic information systems utilized to digitalize contour lines, drainages and watershed. Resulting from the morphometric analysis, a sub-basin area of 28.34 km2 and perimeter distance of 47.4270 km were estimated. The sub-basin is comprised of 22 micro-basins and overall exhibits a form factor value of 0.1171, thus indicating an elongated sub-basin. A compactness coefficient value of 2.4942 indicates an elongated basin. The sub-basin exhibits a concave hypsometric curve, where the peak of its altimetry distribution corresponds to altitudes between 3315 m and 980 m. The slope parameter has an average value of 29.3% slope. It is evident the role played by the Páez River sub-basin for the development of productive activities and water supply of some localities in the province of Cartago.

Keywords: Páez River sub-basin; Morphometry.

Introducción

Uno de los primeros pasos en el análisis hidrológico de cuencas hidrográficas lo constituyen los estudios morfométricos. La morfometría es una de las herramientas más importantes en el analisis hidrico porque permite establecer parametros de evaluacion del funcionamiento del sistema hidrológico de una región (Maidmente, 1992). Asi mismo sirve como análisis espacial en el manejo y planificacion de una cuenca hidrográfica ya que se conocen sus componentes como tamaño de la cuenca, red de drenaje, pendiente media, entre otros aspectos (INE, 2004).

El estudio morfometrico proporciona datos que posibilitan la comprensión del régimen hidrológico, como de las vulnerabilidades a inundaciones, desbordamientos, erosiones y mantenimiento de la red de drenaje (da Costa et al., 2020). También puede referirse a la medición y análisis matemático de la configuración de la superficie terrestre y de su forma y dimensión de sus accidentes geográficos (Biswas et al., 2014).

Las características morfométricas de una cuenca de drenaje proveen la evidencia para describir el comportamiento hidrológico, influencian los procesos hidrológicos (Pothiraj y Rajagopalan 2013, Sing et al. 2014), los geomorfológicos (Poyraz, 2011) y la conservación de suelos y aguas (Asfaw y Workineh, 2019).

Dentro del análisis morfométrico varios de los parámetros se pueden obtener por métodos “a mano”, sin embargo, la forma más precisa y utilizada en la actualidad es a través del uso de un Sistema de Información Geográfica (SIG), donde inicialmente los elementos son obtenidos mediante un MED y se determinan variables como la red de drenaje, aspectos geométricos de la cuenca hidrográfica y aspectos de relieve.

Debido a que los procesos hidrológicos ocurren en la cuenca es de esperar que un análisis numérico-morfométrico pueda proveer información valiosa sobre las características hidrológicas básicas y también brindar más información geológica y geomorfológica de la cuenca (Demoulin, 2011).

Por tanto, para un apropiado manejo y una buena planificación de la subcuenca del rio Páez se requiere un buen entendimiento de los procesos y comportamientos hidrológicos, debido a que en ella el desarrollo de los recursos hídricos está ligado principalmente a actividades productivas como las agrícolas, industriales, comerciales y también al consumo humano. A nivel global y en Costa Rica las investigaciones morfométricas son escasas, destacando únicamente el trabajo reciente de Ramírez y Alfaro (2018), por ello es necesario generar información base detallada que sirva para futuros diagnósticos.

A pesar de la importancia que tiene el análisis morfométrico en los estudios básicos de cuencas hidrográficas, muy pocos investigadores han incorporado este aspecto, sobre todo en cuencas con información limitada. Unido a ello este análisis es un insumo para conocer las condiciones actuales e inventariar el estado de las variables morfométricas de la subcuenca, siendo parte de los primeros pasos para realizar la planificación en cuencas hidrográficas.

Descripción del área de estudio

La subcuenca del río Páez se ubica en la zona noroeste de la cuenca del río Reventazón, al norte se encuentra dentro del área de conservación Parque Nacional Volcán Irazú y al sur con el cantón de Paraíso. Entre las coordenadas planas 515682 y 519780 m este y 1102192 y 1087436 m norte del sistema de Proyección Transversal de Mercator para Costa Rica (Alfaro, 2018).

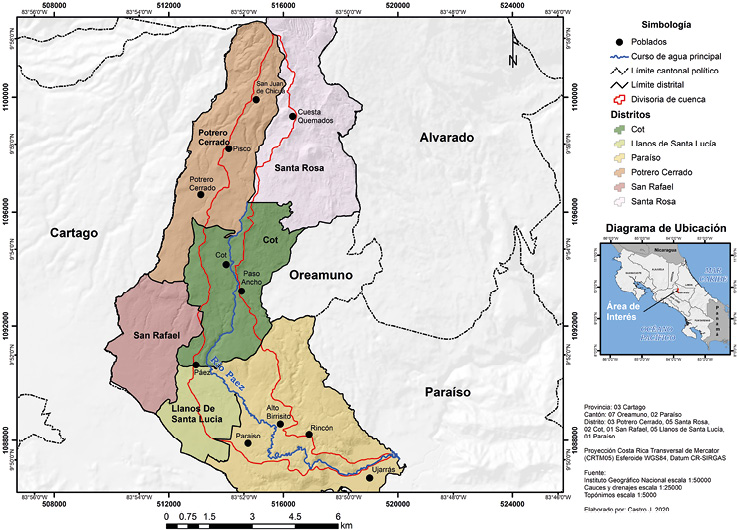
La subcuenca tiene un área de 28,34 km2 se encuentra en los cantones de Oreamuno y Paraíso de la provincia de Cartago, los pueblos que forman parte de ella son Pisco, Cot, Paso Ancho, Páez, San Juan de Chicúa, Cuesta Los Quemados, Paraíso, Finca Ivancovich, Rincón, Alto Birrisito y Ujarrás (Figura 1).

El río Páez es una de las fuentes de abastecimiento de agua potable importante, y es utilizada también para la producción de energía hidroeléctrica, turismo, contribuye al desarrollo de las actividades agrícolas, pecuarias e industriales y a las comunidades. Se evidencia que producto del desarrollo actividades agrícolas y ganaderas en sitios con pendientes muy pronunciadas utilizando prácticas no adecuadas, se ha provocado deterioro al suelo, erosión y contaminación en las fuentes de agua.

Esta zona presenta problemas ambientales con respecto a malas prácticas del uso del suelo, vulnerabilidad y riesgos asociados, inadecuado manejo de residuos sólidos, contaminación de los ríos producto de las actividades agropecuarias, urbanas e industriales, entre otros usos del suelo que se presentan en toda la cuenca.

Metodología

Determinación de parámetros morfométricos

La construcción de la morfometría de la subcuenca se basó en las curvas de nivel del Gran Área Metropolitana (GAM), escala 1:10000 del proyecto PRUGAM. Con uso de los Sistemas de Información Geográfica, ArcGis 10.2® y MapInfo 12®, se realizó la digitalización de las curvas de nivel, los drenajes y el parteaguas. La obtención de los parámetros morfométricos de la subcuenca se calculó numéricamente mediante Microsoft Excel®.

A partir de las curvas topográficas se obtuvo el modelo digital de elevación (MED) y de él, la subcuenca, sus drenajes y sus parámetros de forma. Al considerar la cuenca hidrográfica como un vector poligonal, se calcularon de ella sus propiedades geométricas: área (A), perímetro (P), longitud máxima (Lmax) y ancho máximo (Wmax). Para determinar Lmax se utilizó una circunferencia que envolviera la forma total de la cuenca y para Wmax se obtuvieron polilíneas perpendiculares a los límites de la cuenca para luego calcular la mayor longitud circunscrita en ella. Como parámetro auxiliar, se calculó la longitud y ancho promedio considerando la forma de la cuenca equivalente a un rectángulo.

Sobreponiendo el vector poligonal de la cuenca a los vectores lineales de los contornos topográficos, se calcularon las áreas parciales entre contornos (Ai). Para el caso de los vectores lineales de ríos y contornos topográficos, se calcularon las longitudes de línea para cada uno. De la forma de la cuenca se calcularon los siguientes parámetros:

El Factor de Forma (Ff), definido por Horton (1932) y que representa la relación entre el área y el cuadrado de la longitud de la cuenca, obtenida como:

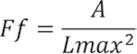
El Coeficiente de Compacidad (k), que representa la relación de P real de la cuenca a un perímetro P´ de un círculo de igual área, fue calculado de acuerdo con la siguiente ecuación:

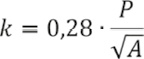
Según Reyes et al. (2010) este indicador está basado en la relación de perímetro de la cuenca con el área del circulo igual al de la cuenca, entre mayor sea el coeficiente, más distante será la forma de la cuenca con respecto del círculo. Cuando son valores cercanos o iguales a uno, corresponde cuando una cuenca presenta tendencia a altos volúmenes de aguas.

La Relación de Circularidad (Rc), la cual representa el cociente entre A de la cuenca y el área (Ac) de un círculo cuya circunferencia es igual a P de la cuenca:

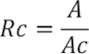
La clasificación de los órdenes de los drenajes fue utilizando el método de Strahler (1957), a partir de ella se obtuvieron la Relación de Bifurcación (Rb), definida como el cociente del número de corrientes del orden dado (Ni) entre el número de corrientes de orden superior inmediato (Ns), este concepto fue definido por Horton (1945), Schumm (1956) y Zavoianu (1985). La longitud de los drenajes se obtiene a partir de las operaciones geométricas básicas de la distancia entre puntos (Bosque, 1997).

La Densidad de Corrientes (Dc), definido como la relación del número total de corrientes a la cuenca de drenaje, es decir representa el número de corrientes por unidad de área, fue computado de la siguiente manera:

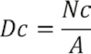
La Densidad de Drenajes (Dd), definida como la densidad de una red de ríos, como la relación de sus longitudes al área de su cuenca hidrográfica, es calculada de la siguiente manera:

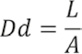
Cuanto mayor sea la densidad de drenaje más rápida será la respuesta de la cuenca frente a una tormenta evacuando el agua en menos tiempo (Reyes et al., 2010).

La curva hipsométrica, se refiere a la representación gráfica del relieve de la cuenca en función de las superficies (Díaz et al., 1999). Para la construcción de dicha curva se lleva a escalas la elevación dada en las ordenadas y la superficie de la cuenca (Reyes et al., 2010).

La pendiente de la cuenca se puede determinar por varios métodos, uno de ellos denominado el criterio de Alvord, este parámetro está basado en la obtención previa de pendientes existentes entre las curvas de nivel, dividiendo el área de la cuenca en áreas parciales por medio de curvas de nivel (Villón, 2004).

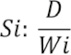
Donde, Si = pendiente media de la faja, D = desnivel entre líneas medias, Wi: ai/Li, ai = área de la faja, Li = longitud de la curva de nivel

El criterio del rectángulo equivalente, también se utiliza para hallar la pendiente de la cuenca (Villón, 2004).

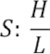
Donde S = pendiente de la cuenca (°), H = desnivel total (m) y L = lado mayor del rectángulo equivalente (km).

Para determinar la pendiente media del cauce, se utiliza el método de compensación, el cual es una manera real de evaluar el pendiente medio del cauce, donde de áreas elige la pendiente de una línea que se apoya en el extremo final del tramo a estudiar y que tiene la propiedad de contener la misma área (abajo y arriba) respecto al perfil del cauce (Villón, 2004).

También se utilizó el criterio Taylor & Schwarz (1952), el cual considera que un río está formado por n tramos de igual longitud, cada uno de ellos con pendiente uniforme (Villón, 2004) de la siguiente manera:

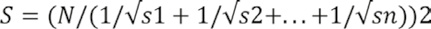
Donde n = número de tramos iguales, en los cuales se subdivide el perfil, S1, S2… Sn = pendiente de cada tramo, según S = H/L, S = Pendiente media del cauce

Resultados

La subcuenca hidrográfica del río Páez presenta un área de 28,3460 km2, obtenida del trazado digital de su parteaguas a partir de curvas de topográficas, cada 5 m. Presenta un perímetro de 47,4270 km y cuenta con una elevación mínima de 980 m y una máxima de 3315 m. El área promedio calculada entre los contornos topográficos es de 0,06070 km2 por cada 5 m de ascenso, con máximos de 0,57402 km2 y mínimos de 0,00048 km2, con una varianza de 0,0047 km2.

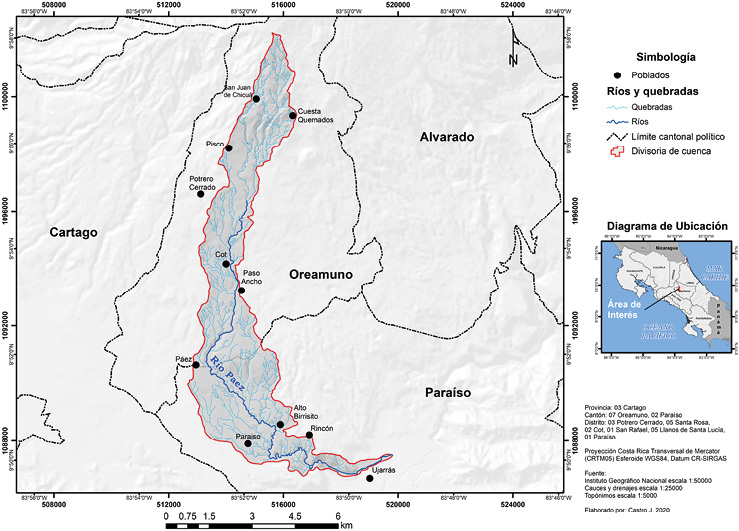
Internamente, la subcuenca del río Páez está compuesta por 22 microcuencas, definidas por el trazado de los drenajes (Figura 2) (cuadro 1) las cuales tienen las siguientes características:

Figura 2. Mapa de drenajes de la subcuenca del río Páez

Cuadro 1. Área y perímetro de 22 microcuencas pertenecientes a la subcuenca del rio Páez, Cartago.

Subcuenca	Área (km2)	Perímetro (km)
1	2,7179	10,7994
2	2,6320	11,6971
3	1,0840	5,6254
4	1,1381	7,6635
5	1,1210	5,3560
6	1,4850	6,5077
7	0,6460	4,1103
8	0,3179	3,7714
9	0,5740	5,2167
10	0,2869	2,8316
11	2,0830	7,5993
12	1,8690	9,1660
13	0,1685	1,8286
14	0,2331	2,2856
15	2,2100	8,4944
16	0,9920	5,2344
17	0,9310	5,8171
18	0,2420	2,4678
19	0,1510	1,7052
20	0,1210	1,9530
21	0,1530	2,0315
22	0,3080	2,5287

Fuente: Elaboración propia.

Las microcuencas tributarias tienen un promedio de área de 0,9887 km2, con un máximo de 2,7179 km y un mínimo de 0,1210 km. La varianza estimada de estas áreas para la cuenca es de 0,6719 km2.

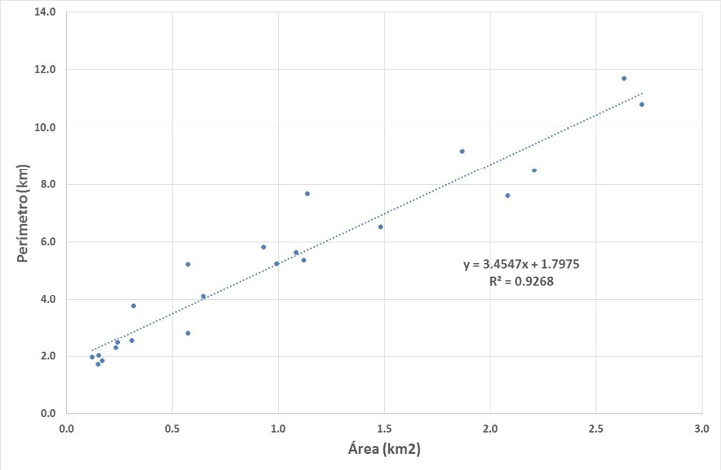
La relación entre el área y el perímetro de las 22 microcuencas se muestra en la figura 3, donde se observa una buena correlación entre ambas propiedades (R2 = 0,9268).

Figura 3. Correlación del área contra el perímetro de las 22 microcuencas, subcuenca del rio Páez.

Fuente: Elaboración propia.

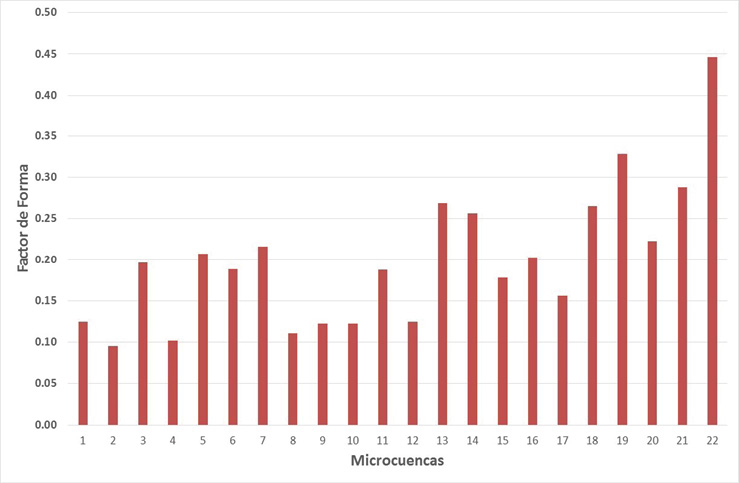
Con respecto a Ff, este es de 0,1171 para la subcuenca en toda su extensión e indica que es una subcuenca alargada. Una cuenca se considera alargada cuando tiene valores menores aproximados a 0.37; en lo correspondiente a las 22 microcuencas, 21 presentan valores menores a 0,35 y por lo tanto se encuentran en el rango de cuencas alargadas. Solo la microcuenca 22 muestra un valor de 0,44 de forma menos elongada, seguido la microcuenca 19 con un valor de 0,33 en. Los valores promedio de las microcuencas están en 0,2004 con una varianza de 0,0069.

De acuerdo con Villón (20004), a mayor Ff mayor posibilidad de tener una tormenta intensa en la cuenca y a menor Ff disminuye la posibilidad de tener una tormenta intensa en la cuenca, como lo es en el caso de la subcuenca Páez (Figura 4).

Figura 4. Valores de Factor de forma para las 22 microcuencas, subcuenca del rio Páez.

Fuente: Elaboración propia.

El parámetro k para la subcuenca del río Páez, muestra un valor de 2,4942. Para las microcuencas que la componen, los valores promedio están en 1,5737 con una varianza de 0,0582. El elemento k es igual a la unidad cuando la forma de la cuenca es un círculo perfecto, incrementándose a 1,128 en el caso de un cuadrado e incluso exceder un valor de 3 para cuencas muy elongadas.

En el caso de la subcuenca del río Páez, sus valores indican que es una cuenca elongada. Internamente, los valores de las microcuencas que son mayormente elongadas son para las microcuencas 2 y 4.

Para el Rc, el cálculo realizado para las 22 microcuenca señala un valor promedio de 0,4250 con una varianza de 0,014. Los valores cercanos a 0,785 indican que la microcuenca puede ser un cuadrado, en este caso solo la microcuenca 22 presenta una forma cercana con un valor de 0,60.

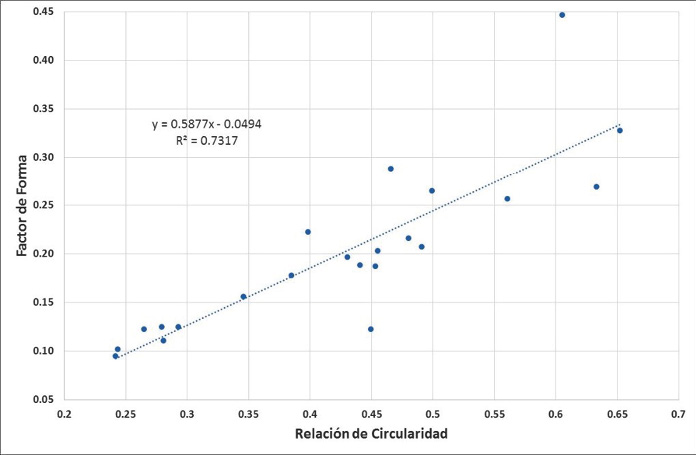
La relación de Rc con respecto a Ff señala un comportamiento creciente, conforme aumentan ambos valores y muestra como las microcuencas más elongadas, presentan valores de Rc más bajos y por tanto siendo un claro indicador del alargamiento de la cuenca (Figura 5).

Figura 5. Correlación del factor de forma contra relación de circularidad de las 22 microcuencas, subcuenca del rio Páez.

Fuente: Elaboración propia.

Análisis hipsométrico y frecuencia altimétrica

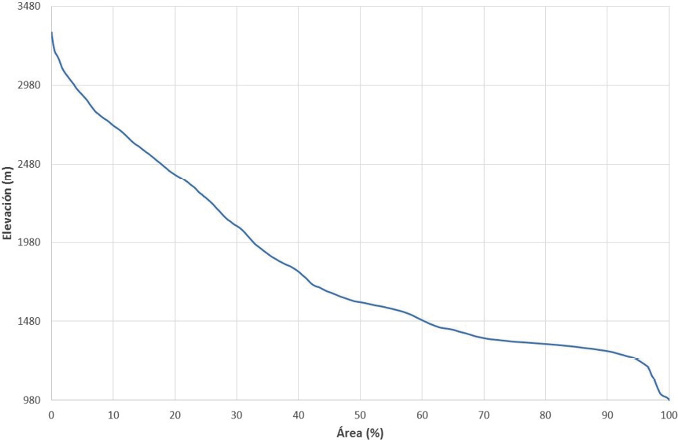
La subcuenca del río Páez muestra una curva hipsométrica de tipo cóncavo, donde el pico de la distribución altimétrica corresponde con las altitudes entre los 3315 m y los 980 m. El valor de la integral hipsométrica, considerando el método propuesto por Pike y Wilson (1971) es de 50%. Este valor revela que la subcuenca del río Páez está iniciando su etapa de madurez, ya que valores cercanos a 47% son asociados a madurez (Racca, 2007). La elevación media de la subcuenca es de 2147,5 m (Figura 6).

Figura 6. Curva hipsométrica de la subcuenca del rio Páez, Cartago.

Fuente: Elaboración propia.

La curva de frecuencia altimétrica muestra una mayor concentración de las áreas de la cuenca en las altitudes entre 1680 m a los 1200 m. La simetría de las áreas respecto a la altitud es evidente desde los 1840 m en la subcuenca (Figura 7).

Figura 7. Curva de frecuencia altimétrica de la subcuenca del rio Páez, Cartago.

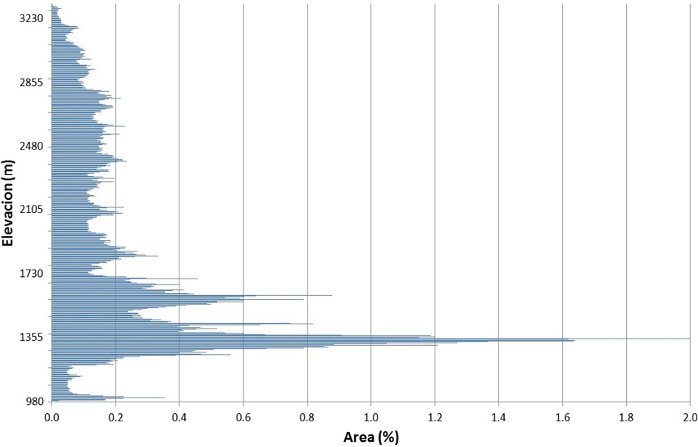
Fuente: Elaboración propia.

Pendiente de la subcuenca

De este parámetro se obtuvo un valor de 29,3% de pendiente promedio, el valor de la pendiente según el criterio de Alvord fue de 22%. Usando el criterio del rectángulo equivalente, el valor de la pendiente para la subcuenca del río Páez fue de 10,4%°. Tomando como base los segmentos del rectángulo equivalente, la pendiente con el criterio de Taylor & Schwarz (Taylor y Schwarz, 1952) resulto un valor de 5,62%.

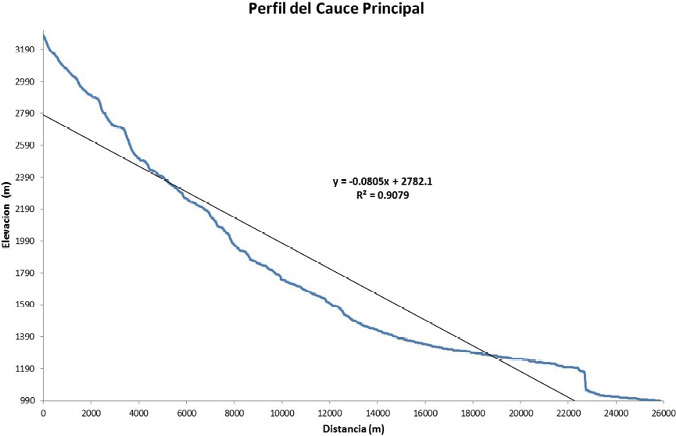
El valor de la pendiente con el método de compensación de áreas fue de 8% con una diferencia entre áreas parciales de 9% (Figura 8). Este valor es coincidente con el criterio del rectángulo equivalente y será el valor promedio de la pendiente de la subcuenca del río Páez.

Figura 8. Perfil longitudinal del cauce principal de la subcuenca del rio Páez, Cartago.

Fuente: Elaboración propia.

En lo que respecta a las 22 microcuencas los valores de pendiente promedio para ellas rondan 11,2% por el criterio de la compensación de las áreas. El método de Alvord sobreestimada el valor de pendiente llegando a alcanzar un 18,9%. Los criterios de Rectángulo Equivalente y Taylor & Schwarz (1952) muestran un 12,84% y un 9,40% respectivamente.

Drenajes

La red de quebradas y ríos son elementos que componen un paisaje geográfico y, por lo tanto, está relacionado con la fragmentación del relieve y con algunos procesos hidrológicos y geomorfológicos.

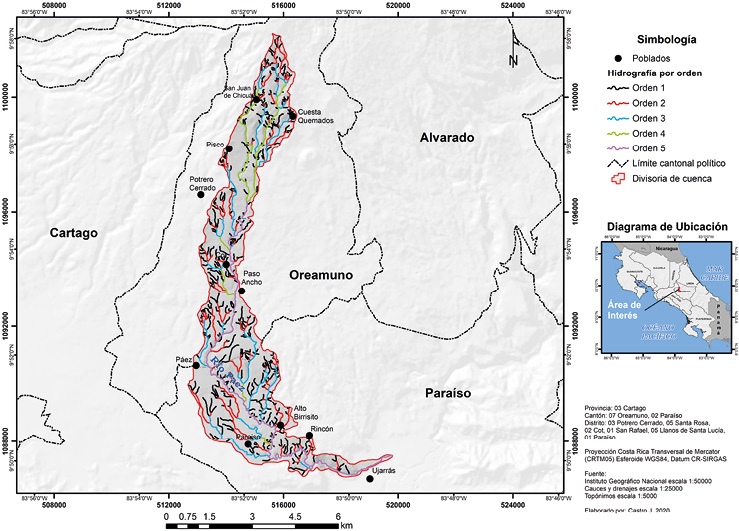
El orden máximo de los drenajes en la subcuenca del río Páez es de 5, en general toda la cuenca los órdenes más numerosos constituyen los de orden 1 seguidos de los de orden 2 (Cuadro 2). Hay 128 corrientes considerando todos los órdenes, dichos órdenes tienden a ser mucho más numerosos en la parte alta de la subcuenca (Figura 9).

Figura 9. Hidrografía por orden de la subcuenca del río Páez, Cartago

Cuadro 2. Órdenes de la subcuenca del rio Páez, Cartago.

Orden	Long. Total corrientes (km)	Numero de corrientes (#)	Relación de bifurcación (#/#)	Long.total corrientes (km)	Media Long. Total corrientes (km)	Relación long (km/km)
1	79,836	453		79,84	0,18
			3,47			1,62
2	34,487	121		34,49	0,29
			2,42			1,91
3	27,266	50		27,27	0,55
			3,85			1,86
4	13,153	13		13,15	1,01
			6,5			9,43
5	19,077	2		19,08	9,54
Total	173,82	639	4,13	173,83	2,31	3,7

Fuente: Elaboración propia.

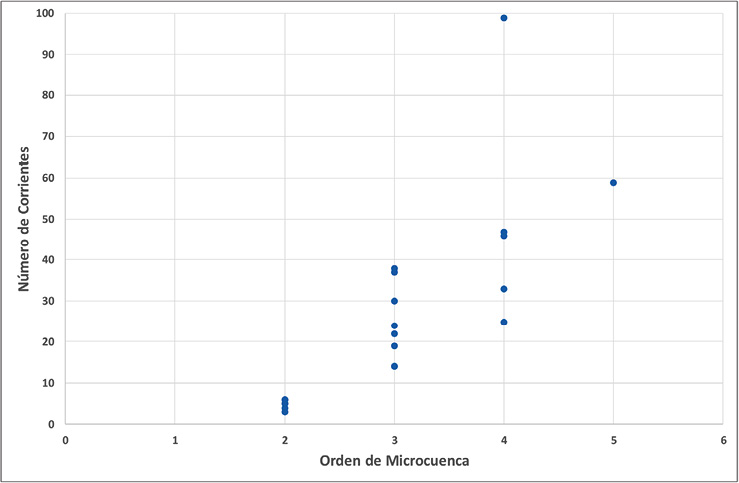
Considerando las 22 microcuencas, la relación entre el orden de cada microcuenca y el número de corrientes en cada una de ellas, esta muestra una tendencia creciente (Figura 10).

Figura 10. Relación órdenes y número de corrientes de la subcuenca del río Páez, Cartago.

Fuente: Elaboración propia.

La Dc, la cual es un indicador importante morfométrico que puede brindar información concerniente a la respuesta de una cuenca de drenaje a procesos de escorrentía. Para el caso de la subcuenca del río Páez, el valor de Dc es de 22,54. En las microcuencas, la densidad de las corrientes tiene un valor promedio de 27,44 con una varianza de 98,62. Las microcuencas con mayor Dc son la microcuenca 9, 17 y 45, todas con valores mayores a 40.

Para el caso de Dd, el valor general para la subcuenca es de 6,13. Para las microcuencas, el valor promedio de Dd es de 6,62, con una varianza de 1,23. En las microcuencas los valores de Dd están entre un máximo de 8,44 y un mínimo de 4,86.

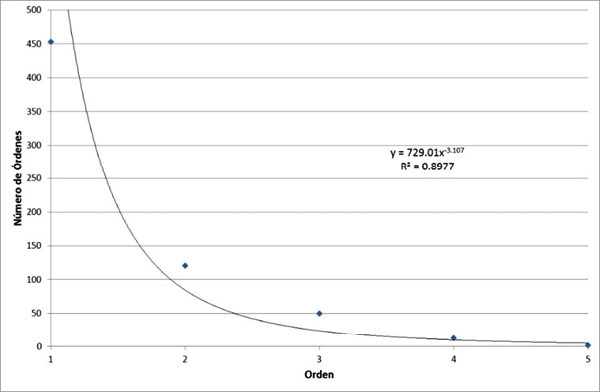
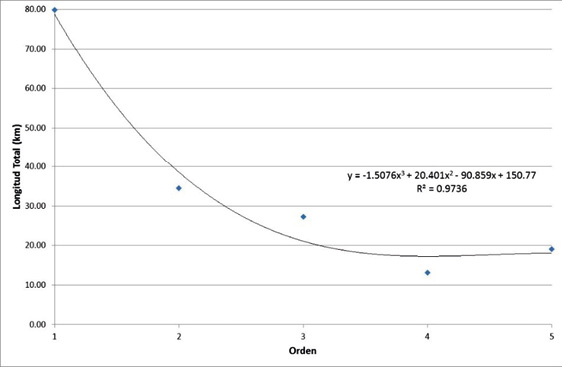
Considerando el número de corrientes y los órdenes se graficó la relación entre ellos y se obtuvo que para la subcuenca del río Páez la relación entre el orden y el número de ellos, responde a una función de potencia (Figura 11). La relación entre los órdenes de las corrientes y su longitud total puede ser descrita por una función polinómica de orden 3 (Figura 12).

Figura 11. Relación órdenes y número de órdenes de la subcuenca del rio Páez, Cartago.

Fuente: Elaboración propia.

Figura 12. Relación órdenes y longitud total de la subcuenca del río Páez, Cartago.

Fuente: Elaboración propia.

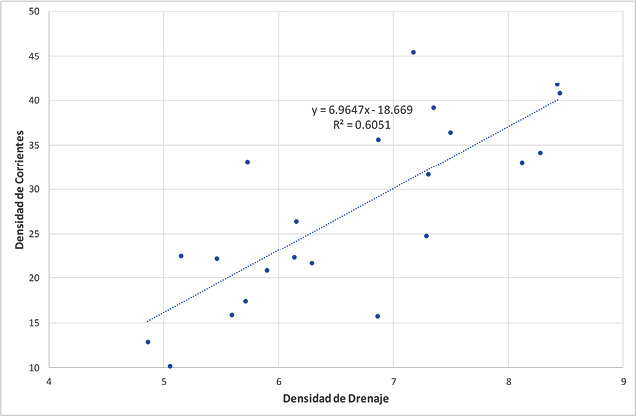
La relación entre Dd y Dc muestra una correlación importante con tendencia al crecimiento conforme se aumentan ambos parámetros morfométricos (Figura 13).

Figura 13. Relación de la densidad de drenajes y densidad de corrientes de la subcuenca del río Páez, Cartago.

Fuente: Elaboración propia.

Conclusiones

El agua que proviene de la subcuenca del rio Páez contribuye al desarrollo de las actividades agrícolas, pecuarias e industriales, producción de energía hidroeléctrica y abastecimiento de agua potable para el cantón de Oreamuno, y algunos sitios Cartago. El análisis morfométrico es fundamental para la planificacion de la subcuenca y Maidment, (1992) plantea que también es una de las herramientas claves en el estudio hídrico porque permite establecer parámetros de evaluación del funcionamiento hidrológico de una región. Así mismo debido a su alto costo en tiempo, también es muy importante como base complementaria a estudios hidrológicos de cuencas, especialmente en cuencas con poca información como lo es en Páez.

Resultado del análisis morfométrico previo se pueden concluir que esta subcuenca tiene un área de 28,34 km2 y un perímetro de 47,4270 km, con una elevación mínima de 980 m y una máxima de 3315 m. Está compuesta por 22 microcuencas, las mismas tienen un promedio de área de 0,9887 km2. El parámetro de Factor de forma tiene un valor de 0,1171 en toda su extensión, indicando una subcuenca alargada, que representa flujos de agua más rápidos.

El coeficiente de compacidad obtuvo un valor de 2,4942, indicando que es una cuenca elongada. Muestra una curva hipsométrica de tipo cóncavo, donde el pico de la distribución altimétrica corresponde con las altitudes entre los 3315 m y los 980 m. Del parámetro pendiente de la subcuenca se obtuvo un valor de 29,3% de pendiente promedio, el valor de la pendiente con el método de compensación de áreas fue de 8%. En lo que respecta a las 22 microcuencas los valores de pendiente promedio para ellas rondan 11,2% por el criterio de la compensación de las áreas.

El orden máximo de los drenajes en la subcuenca del río Páez es de 5, y en general en toda la cuenca los órdenes más numerosos constituyen los de orden 1 seguidos de los de orden 2. Posee una densidad de corrientes es de 22,54, y una densidad de drenaje con un valor de 6,13.

Referencias

Asfaw, D. & Workineh, G. (2019). Quantitative analysis of morphometry on Ribb and Gumara watersheds: Implications for soil and water conservation. International Soil and Water Conservation Research 7, pp. 150-157.

Biswas, A; Majumdar, D. & Banerje, S. (2014). Morphometry governs the dynamics of drainage basin: Analysis and implications. Hindawi Publishing Corporation Geography Journal, pp. 1-14.

Bosque, J. (1997). Sistemas de Información Geográfica. Ediciones Rialp. Madrid, p. 451.

Da Costa, A. A. D., Dos Santos Galvanin, E. A. & Da Silva Neves, S. M. A. (2020). Análise Morfométrica Da Bacia Hidrográfica Paraguai/Jauquara, Mato Grosso - Brasil. Geosul, 35(74), pp. 483-500. https://doi-org.una.idm.oclc.org/10.5007/1982-5153.2020v35n74p483

Demoulin, A. (2011). Basin and river profile morphometry: A new index with a high potential for relative dating of tectonic uplift. Geomorphology. 126, 97-107.

Díaz C, Mamado K, Iturbe A, Esteller, MA. & Reyna F. (1999). Estimación de las características Fisiográficas de una Cuenca con la ayuda de SIG y MEDT Caso del Curso Alto del Rio Lerma, Estado de México. Ciencia Ergo Sum 6 (2), 124-134.

Horton, R. (1932). Drainage-basins characteristics. Transactions American Geophysical Union, 350-361.

Horton, R. (1945). Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geological Society of America Bulletin 56, 275-370.

Instituto Nacional de Ecología (INE). (2004). Análisis morfométrico de cuencas: caso de estudio del Parque Nacional Pico de Tancítaro. México: Dirección General de Investigación de Ordenamiento Ecológico y Conservación de Ecosistemas, p. 47.

Maidment, D. R. (1992). Handbook of Hydrology, McGraw-Hil. Inc., New York, NY.

Pike, R. J., & Wilson, S. E. (1971). Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Geological Society of America Bulletin, 82(4), 1079-1084.

Pothiraj, P; Rajagopalan, B. (2013). A GIS and remote sensing-based evaluation of groundwater potential zones on a hard rock terrain of Vaigai sub-basin, India. Arabian Journal of Geosciences 6, 2391-2407.

Poyraz, M; Taskin, S. & Keles, K. (2011). Morphometric approach to geomorphologic characteristics of Zeytinli stream basin. Procedia Social and Behavioral Sciences 19, pp. 322-330.

Racca, J. (2007). Análisis hipsométrico, frecuencia altimétrica y pendientes medias a partir de modelos digitales del terreno. Boletín del Instituto de Fisiografía y Geología, 77 (1-2), 31-38.

Ramírez, P. & Alfaro, K. (2018). Morfometría de la subcuenca del río Toyogres, Cartago, Costa Rica. Revista Geográfica de América Central, 60, 255-275.

Reyes, A; Barroso, F. & Carvajal Y. (2010). Guía Básica Para La Caracterización Morfométrica de Cuencas Hidrográficas. Programa Editorial Universidad del Valle, Colombia, p. 83.

Schumm, S. (1956). Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Bulletin of the Geological Society of America 67, 597-646.

Singh, P; Gupta, A; Singh, M. 2014. Hydrological inferences from watershed analysis for water resources management using remote sensing and GIS techniques. The Egyptian Journal of Remote Sensing and Space Sciences 17: 111-121 p.

Strahler, A. (1957). Quantitative analysis of watershed geomorphology. Transaction American Geophysical Union 38 (6), 913-920.

Taylor, A. & Schwarz, H. (1952). Unit-hidrograph lag and peak flow related to basin characteristic. Transactions American Geophysical Union. 33 (2), 235-246

Villón, M. (2004). Hidrología. San José, Costa Rica: Editorial Tecnológica de Costa Rica.

Zavoianu, I. (1985). Morphometry of Drainage Basins. Developments in Water Science, 20. Elsevier.

---