| ISSN Electrónico: 2215-3470 DOI: http://dx.doi.org/10.15359/ru.33-2.3 |
UNICIENCIA Vol. 33, N° 2. Julio-Diciembre, 2019 URL: www.revistas.una.ac.cr/uniciencia Correo electrónico: revistauniciencia@una.cr |
 |
 |
Evidencias sobre algunas tendencias pedagógicas y didácticas presentes en los programas de estudio de matemáticas costarricense |
Evidence on some pedagogical and didactic trends present in the Costa Rican mathematics curriculum
Evidências sobre algumas tendências pedagógicas e didáticas presentes nos programas de estudo de matemática costarriquenha
Marianela Zumbado-Castro
mazumbado@uned.ac.cr
Universidad Estatal a Distancia,
San José, Costa Rica.
Orcid: https://orcid.org/0000-0002-5774-1884
Recibido-Received: 1/jun/2018 ● Corregido-Corrected: 15/set/2018.
Aceptado-Accepted: 20/set/2018 ● Publicado-Published: 31/jul/2019.
|
Resumen Las tendencias pedagógicas y didácticas que se presentan en los programas de matemáticas orientan el estilo de organización de las lecciones propuesto por el Ministerio de Educación Pública de Costa Rica a partir de 2012. Cada momento de la clase está fundamentado en ideas de diversas fuentes: constructivismo, socioculturalismo, pragmatismo realista, educación matemática realista; además, en ideas japonesas, francesas y norteamericanas. En este documento, se pretende presentar el vínculo entre la teoría y las acciones que se pueden desarrollar con los estudiantes, a través del planteamiento de un problema, la resolución de este y el trabajo del docente, de acuerdo con la propuesta costarricense. Se puede establecer que hay presencia e impacto de cada tendencia al vivenciar los momentos propuestos para trabajar en el aula, debido a que es sólida la fundamentación y se ofrece un respaldo teórico e histórico consolidado, por lo tanto, se puede depositar la confianza en la propuesta metodológica. Palabras clave: reforma de la educación; plan de estudios; aprendizaje; tendencia educativa; enseñanza de las matemáticas; estrategia de enseñanza. Abstract The pedagogical and didactic trends present in the Costa Rica math curriculum have led the style of the lesson organization proposed by the Ministry of Public Education since 2012. Every step in the class is based on ideas from different sources: constructivism, socioculturalism, realistic pragmatism, realistic mathematical education, as well as Japanese, French and American ideas. This paper aims to present the link between theory and the actions that can be performed with students by posing a problem, solving it, and having the teacher’s assistance, as proposed in the Costa Rican curriculum. It can be established that each trend is present and produces an impact when performing each step proposed for classwork since the foundation and the historical and theoretical backgrounds are solid; therefore, the methodological proposal can be trusted. Keywords: education reform; curriculum; learning; education trend; math education; teaching strategies. Resumo As tendências pedagógicas e didáticas apresentadas nos programas de matemática orientam o estilo de organização das lições propostas pelo Ministério da Educação Pública da Costa Rica a partir de 2012. Cada momento da aula é baseado em ideias de diferentes fontes: construtivismo, socioculturalismo, pragmatismo realista, educação matemática realista; também, em ideias japonesas, francesas e norte-americanas. Neste documento, pretendemos apresentar a ligação entre a teoria e as ações que podem ser desenvolvidas com os estudantes, através da abordagem de um problema, a resolução deste e o trabalho do professor, de acordo com a proposta costarriquenha. Pode-se estabelecer que existe a presença e o impacto de cada tendência para vivenciar os momentos propostos para trabalhar em sala de aula, pois o fundamento é sólido e oferece respaldo teórico e histórico, portanto a confiança pode ser depositada na proposta metodológica. Palavras-chave: reforma da educação; plano de estudos; aprendizagem; tendência educacional; ensino de matemática; estratégia de ensino. |
Este documento pretende establecer la relación entre algunas tendencias pedagógicas y didácticas con la fundamentación teórica de los programas oficiales de matemáticas costarricenses, mediante el análisis documental y la presentación de un ejemplo de aula. Este proceso permitirá responder a preguntas puntuales: ¿cuáles son las tendencias pedagógicas y didácticas que orientan los programas oficiales?, ¿cuál es el vínculo entre ellas y la estrategia metodológica de resolución de problemas planteada por el MEP?, ¿cómo se pueden ejemplarizar a través de los programas oficiales? Y, finalmente, ¿cuáles ventajas se pueden identificar en las tendencias pedagógicas y didácticas?
Lo anterior ofrecerá un texto que analiza las tendencias curriculares manifestadas en el transcurso histórico inmediato de la educación matemática internacional y sus implicaciones en el currículo nacional vigente (UNED, 2017). Además, se toma en consideración la reforma curricular reciente y las características tanto propias como particulares de los programas aprobados en el 2012 para el país.
Corrientes filosóficas en las que se enmarcan los programas de estudio de matemáticas
Se dará inicio a este apartado con el análisis de la política educativa “Hacia el Siglo XXI”, aprobada en 1994 y vigente hasta el 2016, debido a que los programas fueron elaborados considerando sus elementos teóricos.
Sin embargo, se debe destacar que se puede establecer la coherencia entre la nueva política educativa denominada “La persona: centro del proceso educativo y sujeto transformador de la sociedad” (MEP, 2017, pp. 8-10), cuyo marco filosófico y conceptual contiene el paradigma de la complejidad, el humanismo, el constructivismo social y racionalismo, pero ese análisis no está entre los alcances de este documento.
En la política educativa costarricense entre 1994 y el 2016, se asumían tres corrientes filosóficas: humanismo, racionalismo y constructivismo; de esta última fuente se toma el enfoque centrado en el estudiante con un papel activo, en el que el aprendizaje avanza mediante progresos cognitivos (MEP, 2012). Por lo tanto, el constructivismo será analizado con detalle, para tratar de establecer las tendencias pedagógicas y didácticas vinculadas con los procesos de enseñanza y aprendizaje que se amparan bajo esa corriente.
A continuación, una breve descripción de las fuentes, según el Consejo Superior de Educación de Costa Rica (1994):
•Humanismo: Se asume al ser humano como persona dotada de dignidad y con la capacidad de buscar la perfección en el ambiente que procure la legislación educativa, de manera individual y social (MEP, 2012).
•Racionalismo: Se reconoce al ser humano como la capacidad racional para comprender objetivamente la realidad, tanto construir como perfeccionar los saberes y colaborar con el progreso y la comunicación (MEP, 2012).
•Constructivismo: Se asume que la educación parte de la “situación cognoscitiva del alumno, de su individualidad, de sus intereses e idiosincrasia” (p. 486), entonces se debe reconocer la cultura específica y las estructuras de conocimiento. Finalmente, es preciso realizar acciones formativas para el alumno y el conocimiento que los transforme mutuamente (MEP, 2012).
A continuación, se profundizará en el análisis de los fundamentos de los programas para establecer la relación entre estos y las tendencias pedagógicas y didácticas que orientan la propuesta para los procesos de enseñanza y aprendizaje de las matemáticas en Costa Rica.
Tendencias pedagógicas presentes en los programas de estudio de matemáticas y su relación con el estilo para organizar las lecciones
El estilo para organizar las lecciones, propuesto por el MEP, considera dos etapas con propósitos diferentes: la 1, el aprendizaje de conocimientos y la 2, la movilización y aplicación de los conocimientos. Asimismo, para la etapa 1, se sugieren cuatro pasos o momentos denominados: “Propuesta de un problema, Trabajo estudiantil independiente, Discusión interactiva y comunicativa y finalmente Clausura o cierre” (2012, p. 41-43). A continuación, se intentará establecer la relación entre estos momentos y las tendencias pedagógicas y didácticas.
Constructivismo y educación matemática
En el periodo entre 1986 y 1995, según el MEP (2012), hay al menos tres fuentes en las que se sustenta la educación matemática, dos de ellas consideradas tradicionales: la resolución de problemas, errores, falsas creencias y obstáculos epistemológicos, y las teorías de desarrollo cognitivo. Inclusive, se afirma que “Se trata de una corriente epistemológica que enfatiza el papel del sujeto en la construcción cognoscitiva” (p. 486).
Según el MEP (2012), existe un alto grado de coincidencia entre los trabajos de Piaget y la forma en la que se plantean los programas de matemáticas; para evidenciarlo, citan a Ruiz (2000) de la siguiente forma:
En Piaget: el sujeto es el factor activo. Para Piaget existe una “abstracción reflexiva”, que define como una generalización operatoria. Es esta clase de abstracción la que le permite proponer etapas mentales definidas por medio de estructuras mentales. Este asunto de las etapas es uno de los temas más conocidos sobre sus ideas epistemológicas. Para Piaget, las acciones del sujeto y no del objeto son las claves. El objeto posee un rol secundario: ofrecer circunstancias sobre las que el sujeto interviene. En este mundo teórico el sujeto puede coordinar y combinar sus acciones. ¿Qué crea el conocimiento matemático? Su respuesta es inequívoca: la acción y operación mentales (MEP, 2012, p. 486).
Desde este momento, es posible hacer una conexión con la manera en que el MEP (2012, pp. 41-43) plantea el estilo para la organización de las lecciones y también con uno de sus ejes disciplinares, “La resolución de problemas como estrategia metodológica principal” (MEP, 2012, p. 35). Se puede analizar este planteamiento con detalle, hay tres elementos por considerar: las estructurales mentales, las acciones del sujeto y el objeto.
El objeto es un ente pasivo con un rol secundario, pero que debe propiciar las condiciones para que el estudiante intervenga; esto se puede lograr a través de un problema que pretende instar algún conocimiento matemático. Se debe entender que el objeto es el conocimiento y las condiciones para la intervención del sujeto están en un problema (contextualizado o no contextualizado). Esta interacción implica emplear las estructuras mentales existentes o modificarlas, a través del proceso de resolución del problema, cuyos procedimientos de pensamiento son matemáticos, por tanto, con esto se consigue un progreso cognitivo.
El MEP (2012) reafirma su posición a través de Radford (2008), al emplear premisas epistemológicas del constructivismo, que según este ministerio tiene sus orígenes en Kant. Se establece que son tres: “el conocimiento no se recibe de manera pasiva por el sujeto, sino que es construido, la función cognitiva es adaptativa y sirve a la organización de la experiencia y no a la descripción de una realidad ontológica” y tercero, “el sujeto construye su conocimiento de manera autónoma” (MEP, 2012, p. 486).
Finalmente, se afirma sobre este asunto que “el objeto epistémico es en el constructivismo una oportunidad para la acción del sujeto” (MEP, 2012, p. 486). Esto permite establecer una primera aproximación a otro vínculo con dos momentos que organizan la lección según el ente ministerial, el primero llamado “propuesta de un problema” y el segundo denominado “trabajo estudiantil independiente”. Este último se describe como una fase que ofrece tiempos para el trabajo individual, en parejas o en subgrupos, para apropiarse del problema, establecer estrategias de solución, realizar investigación y ensayos; se permite a los estudiantes enfrentar el problema por sí mismos y esta confrontación es la que produce un aprendizaje significativo (MEP, 2012).
Se sigue, entonces, que con las acciones planteadas para este momento de la clase (trabajo estudiantil independiente), se potencian las oportunidades para permitirle al sujeto tener un rol participativo en el proceso de su aprendizaje.
Sin embargo, el MEP (2012), establece que en el constructivismo asumido en la política educativa (Radford y Kant) se hace un énfasis en las construcciones cognitivas individuales, se minimiza el papel de la sociedad y la cultura, así como se limita el papel docente.
Tradición epistemológica: socioculturalista
Se plantea la necesidad de incluir otras ideas sobre el sujeto, así como de justificar la importancia y requerimiento de las otras personas o circunstancias en el aprendizaje individual, entre ellas el docente y la mediación pedagógica. Entonces, el MEP (2012) incluye en los programas de matemáticas otra tradición epistemológica, la socioculturalista, la cual se vincula con el pensamiento de Vygotsky (1978), el cual también invita a incluir los aspectos emocionales en el aprendizaje (MEP, 2012).
Además, incluye fuentes provenientes de la educación matemática. Se afirma que, desde mediados de los años 90, se ha dado importancia “al lenguaje, la cultura, los métodos, fines y medios que han construido la sociedad” (MEP, 2012, p. 487) y que esto ha permeado la forma de enfocar la acción de aula. El papel docente y la interacción tanto colectiva como social han sido revalorados porque no son únicamente medios para construir conocimientos, sino que son factores que intervienen en el proceso.
Con base en lo anterior, queda en evidencia la concordancia de estas ideas y el estilo para la organización de las lecciones propuesto por el MEP (2012). Se plantean cuatro fases o momentos, de los cuales se han mencionado dos, “propuesta de un problema” y “trabajo estudiantil independiente”, pero ahora se justifica la presencia de los momentos denominados “discusión interactiva y comunicativa” y “clausura o cierre”. Lo anterior debido a que en la acción de aula durante estas fases se promueve el intercambio de ideas entres los estudiantes, una validación entre iguales de las estrategias de solución empleadas de manera exitosa o no exitosa, donde al final del proceso hay una interacción entre el docente y los alumnos para formalizar los conocimientos matemáticos. Se sigue que existe una construcción de conocimientos durante todas las fases y que el vínculo entre los sujetos participantes es natural y necesario.
Asimismo, el MEP (2012) señala, a través de las ideas de Michèle Artigue (2011), que actualmente ha habido transformaciones en las perspectivas educativas, las cuales plantean que la investigación internacional, comenzada con el alumno como centro, se ha desplazado hacia el docente para darle un rol protagónico en la didáctica de la matemática. Al respecto, son de interés sus creencias sobre el aprendizaje, las calidades de sus conocimientos y la forma en que ejecuta sus prácticas de enseñanza. Además, Artigue indica que se trasladó el interés a los procesos de formación inicial de los docentes y sus efectos. Se debe señalar que estas ideas aplicadas al currículo nacional se traducen en la necesidad de tener personal docente con un adecuado dominio de los contenidos en el nivel matemático y pedagógico, para efectuar “el cierre o clausura” de la clase de manera idónea.
Continuando con el constructivismo, existen otros señalamientos del MEP (2012) hacia algunos faltantes en la vertiente cognitiva de aquel, en cuanto a la educación matemática. Esta última implica la presencia de las notaciones, convenciones sobre procedimientos o algoritmos y estos no requieren construcciones cognitivas, por tanto, son independientes a la intervención del sujeto. La razón es porque para algunos procedimientos matemáticos no es conveniente enfrentar a los estudiantes con sus orígenes epistémicos, debido a que didácticamente no es lo que se persigue o puede generar obstáculos.
Por eso, también se incluye la posición adoptada por Lesh y Doerr (2008), quienes señalan que existen al menos cuatro distintos tipos de objetivos instruccionales para la educación matemática y que no todos necesitan la construcción independiente del estudiante:
•objetivos de conducta (OC) como los simples hechos y destrezas;
•objetivos de proceso (OP) como los hábitos de mente que no están conectados a ningún constructo particular matemático;
•objetivos afectivos (OA) como actitudes, creencias, sentimientos, y
•objetivos cognitivos (OC) como los modelos y sistemas conceptuales que los acompañan (constructos) para construir, describir, explicar, manipular y controlar matemáticamente (MEP, 2012, p. 488).
Por lo tanto, se concluye que hay un nuevo paradigma, en el que contribuye la educación matemática con elementos específicos de la disciplina, que implica la integración del constructivismo y las perspectivas del socioculturalismo. Los programas de matemáticas de 2012 se construyeron con estas perspectivas y estarán albergados en ese paradigma; al respecto, el MEP (2012, p. 88) coincide con la idea de “un paradigma emergente”.
El MEP (2012) indica que no es posible ubicarse en un único conjunto de ideas, sugiere mantener una posición flexible para incorporar otros elementos teóricos que se requieran para dar respuesta a las necesidades educativas.
Pragmatismo realista
El MEP plantea, también, un acercamiento al pragmatismo realista y usa a Cobb (1994) para respaldar la posición “el aprendizaje matemático debe verse como un proceso de construcción activa individual a la vez que un proceso de enculturación de prácticas matemáticas de una sociedad más amplia” (MEP, 2012, p. 488).
Esta última aproximación teórica se vincula, nuevamente, con el estilo de lección propuesto y con otro eje disciplinar “La contextualización activa como un componente pedagógico especial” (MEP, 2012, p. 17). Se establece otra vez la construcción del conocimiento con una participación activa y esto se puede lograr mediante los cuatro momentos que indica el mismo MEP (2012). Respecto al eje disciplinar citado, la frase “enculturación de prácticas matemáticas” pone de manifiesto un conjunto de ideas que se relacionan con el entorno y la cultura matemática. Bishop (1999) indica que existen al menos seis actividades universales esenciales para desarrollar las matemáticas en la cultura: contar, localizar, medir, diseñar, jugar y explicar. Esas acciones se logran de manera natural, a través de la interacción con la realidad, en particular, mediante la resolución de problemas en contextos reales. Por tanto, se habla de un componente pedagógico importante para aplicar la estrategia metodológica que propone el MEP (2012).
Sobre este eje disciplinar, el MEP (2012) señala que existe un vínculo estrecho entre la resolución de problemas como estrategia metodológica principal y la contextualización activa como un componente pedagógico especial, porque estimula la acción estudiantil; igualmente, propone el uso de “modelos sobre la realidad cercana” (p. 36).
Del mismo modo, se plantea que la contextualización activa puede ser modelización y se aconseja diseñar problemas obtenidos de información de la prensa, de la escuela, de la comunidad, de la clase, de diversas áreas disciplinares (estudios sociales o ciencias, por ejemplo) o de Internet. Además, se señala que no todos los problemas deben ser de modelización, pero estos son fundamentales, porque evidencian la utilidad, el significado de los objetos e implican usar las habilidades matemáticas e ir, de manera progresiva, en el desarrollo cognitivo; aquí se demuestran, según el MEP (2012), “los andamios para la construcción de los aprendizajes desde lo concreto hacia lo abstracto” (p. 36) y con esto se hace referencia, nuevamente, al pensamiento de Vygotsky.
Tendencias didácticas presentes en los programas de estudio de matemáticas y su relación con el estilo para organizar las lecciones
Continuando con el estilo de organización de las lecciones, es necesario puntualizar algunos elementos. El MEP (2012) señala, específicamente, algunas fuentes que inspiraron la propuesta.
Experiencias e investigaciones nacionales revelaron lo siguiente:
•La acción de aula en el país emplea procedimientos rutinarios y escaso trabajo en el desarrollo de capacidades cognitivas superiores (Programa Estado de la Nación, 2011; SERCE, 2008; Chaves Esquivel et al., 2010).
•Se emplea un estilo de lección que no motiva el interés estudiantil y tampoco la construcción de los aprendizajes (Ruiz, Barrantes y Gamboa, 2009).
•Se requiere una formación docente en sintonía con características de una lección distinta a la que se desarrolla mayoritariamente en las aulas costarricenses.
Es evidente que cada uno de esos resultados encuentra una respuesta en la propuesta del MEP (2012), la resolución de problemas implica una ruptura de procedimientos rutinarios, que lleva a acciones cognitivas de otro nivel y que puede promover mayor interés en la clase de matemáticas (Espinoza y Zumbado, 2015). Asimismo, hay resultados que respaldan la necesidad de brindar formación al docente sobre nuevas estrategias metodológicas (posición que también puntualiza Artigue), que permitan conseguir actividades de mayor exigencia y promuevan el interés, ambos elementos vinculados con otro eje disciplinar: “la potenciación de actitudes y creencias positivas en torno a las Matemáticas” (MEP, 2012, p. 17).
Además de los resultados hallados en la literatura en Costa Rica, existe un marco de referencia internacional, del cual se retoman algunas nociones y se incorporan en la propuesta:
•Ideas de la OCDE en el marco teórico de las pruebas PISA.
•Los planteamientos teóricos de la corriente de Educación Matemática Realista (EMR) de H. Freudenthal (1973, 1983, 1991).
•La experiencia de Japón.
•Algunos resultados de investigación de la escuela de didáctica de las matemáticas en Francia (MEP, 2012, p. 499).
Evidencia de las tendencias pedagógicas y didácticas en los programas de 2012
Hasta el momento, se han abordado los fundamentos teóricos de los programas, se han considerado los apartados sobre el plan de estudio, su organización, la perspectiva, los procesos, la mediación pedagógica y la resolución de problemas, así como las notas aclaratorias en las páginas finales. En todos ellos se muestra un conjunto de ideas sobre las cuales se basa la propuesta y explicaciones que amplían la exposición de esas ideas. A continuación, se pretende presentar evidencias de las tendencias analizadas previamente, en la ejecución de la estrategia metodológica de resolución de problemas y en algunos otros elementos de la malla curricular.
Se empleará un plan de lección elaborado con base en los cuatro momentos planteados según el estilo de organización de las lecciones indicado por el MEP (2012).
Plan de lección para octavo año
Se empleará la siguiente habilidad específica del programa oficial y se efectuará una modificación al problema planteado en las indicaciones puntuales.

Figura 1. Problema contextualizado para sétimo año que implica función lineal
Extraído de: Programas oficiales del MEP, 2012, p. 331.
Conocimientos previos del área de relaciones y álgebra
•Cuarto grado: Analizar patrones en sucesiones con figuras, representaciones geométricas y en tablas de números naturales menores que 1 000 000 (MEP, 2012, p. 232).
•Quinto grado: Relaciones, cantidades constantes, cantidades variables, dependencia, independencia de variables (MEP, 2012, p. 234).
•Sexto grado: Representaciones algebraicas (MEP, 2012, p.240) y analizar sucesiones y patrones con números, figuras y representaciones geométricas (MEP, 2012, p. 239).
•Sétimo año: Representaciones, tabular y gráfica (MEP, 2012, p. 330).
Propuesta del problema
|
Tarifa para el servicio de taxi A partir del 1 marzo de 2018, rige la siguiente tarifa para el servicio de taxi, decretada por la Autoridad Reguladora de los Servivios Públicos (ARESEP), 660 colones para el primer kilómetro y 620 para cada kilómetro adicional. a. Represente, mediante una tabla, la cantidad de dinero que se debe pagar por la distancia recorrida en kilómetros, de acuerdo con la tarifa de la ARESEP. Comience a realizar los cálculos a partir del segundo kilómetro. b. Plantee una representación algebraica que sirva de modelo para esta situación. c. Represente, en un sistema de ejes cartesianos, la relación descrita en el problema anterior. d. Usted debe pagar 13 800 colones. ¿Cuántos kilómetros, aproximadamente, debió recorrer para que tuviera que pagar ese monto, según la tarifa de la ARESEP? |
Solución del problema de acuerdo con cada pregunta durante el trabajo estudiantil independiente
Se espera que un estudiante de octavo realice acciones semejantes a las planteadas a continuación, tal vez en subgrupos de trabajo:
a)Represente, mediante una tabla, la cantidad de dinero que se debe pagar por la distancia recorrida en kilómetros. Comience a realizar los cálculos a partir del segundo kilómetro.
Tabla 1
Distribución de cantidad de kilómetros y monto por pagar en la tarifa para el servicio de taxi
|
Cantidad de kilómetros |
Operación |
Monto por pagar |
|
2 |
660 + 620 |
1280 |
|
3 |
660 + 620 + 620 |
1900 |
|
4 |
660 + 620 + 620 + 620 |
2520 |
|
5 |
660 + 620 + 620 + 620 + 620 |
3140 |
|
. . |
. . |
. . |
Nota: Fuente propia de la investigación.
b)Plantee una representación algebraica que sirva de modelo para esta situación.
Si recorro 5 kilómetros, puedo calcular el monto por pagar con esta expresión: 660 + 4 x 620, uso un kilómetro menos, porque el primero ya ha sido calculado y tiene un costo menor, entonces, se puede representar de la siguiente forma: 660 + (n – 1) x 620, si n representa el número de kilómetros.
c)Represente, en un sistema de ejes cartesianos, la relación descrita en el problema anterior.
Gráfica 1
Distribución de cantidad de kilómetros por monto que se debe pagar según la tarifa para el servicio de taxi de la ARESEP, 2018
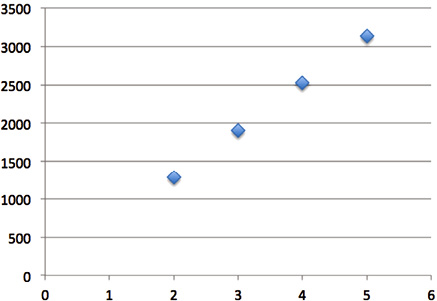
Nota: ARESEP, 2018.
d)Si usted debe pagar 13 680 colones, ¿cuántos kilómetros, aproximadamente, debió recorrer para que tuviera que pagar ese monto?
Se espera que los estudiantes, mediante ensayo y error, encuentren la respuesta o, a través de los datos consignados en la tabla, logren hallar una aproximación. Por ejemplo, si 5 kilómetros implican 3140 colones, entonces deberá recorrer más de 20 kilómetros, debido a que 3140 x 4 = 12560 y estas acciones implican pensamiento inverso. Asimismo, se puede esperar que los estudiantes hallen la respuesta exacta que corresponde a 22 kilómetros.
Se debe señalar que, durante este momento, el docente supervisa el trabajo de los estudiantes y atiende sus consultas. En caso de que ellos presenten algún “estancamiento”, el docente planteará preguntas para que ellos mismos o con sus iguales determinen la respuesta a la pregunta o encuentren una estrategia para hallar la respuesta.

Figura 1. Estudiantes del Liceo Ing. Samuel Sáenz Flores, durante el trabajo estudiantil independiente
Extraído de: Proyecto Reforma de la Educación Matemática en Costa Rica, 2015.
Antes de continuar con los otros momentos de la clase, es necesario señalar aquí las tendencias pedagógicas y didácticas presentes, las cuales se mezclan en la ejecución de una clase. El problema es una situación contextualizada, con eventos que pueden ser cercanos a los estudiantes, como lo es “tomar un taxi”; esto pone en manifiesto el pragmatismo realista y el uso de la modelización de manera conjunta.
El pragmatismo expone que la intervención de la persona en diversas formulaciones como lo es un problema no implica un comportamiento absoluto, “sino hipotético y práctico de los principios teóricos” (Soto y Bernardini, 2007, p. 216), como el de un estudiante durante su solución. Esta tendencia pedagógica enfatiza la perspectiva práctica de cualquier ciencia, en este caso, de las matemáticas.
Al continuar con el análisis de la solución, se evidencia que los estudiantes deben usar sus conocimientos previos para enfrentar el problema y la pregunta para nuestro análisis es cómo el uso de esos conocimientos previos será la base para adquirir nuevos saberes; esta respuesta se presentará más adelante. Sin embargo, ahora el interés es mostrar el andamiaje presente en esta construcción de aprendizajes provocada por una situación real, que persigue la respuesta general a la pregunta: ¿cuánto costará un recorrido de x kilómetros?
Asimismo, existe aquí una relación directa con el EMR, debido a que Freudenthal, citado por Gravemeijer y Teruel (2000), expone que “las matemáticas deben ser enseñadas como matematización” (p. 779). Esto significa que lo que se enseña en las aulas debe ser seleccionado por su utilidad, debido a que los objetos matemáticos son necesarios en todas las actividades humanas. Asimismo, Freudenthal plantea que es más importante hacer matemáticas que entregarlas como un producto terminado. Esto se puede observar en las actividades planteadas en este problema: completar tablas, responder preguntas y emplear pensamiento inverso, para poder, posteriormente, descubrir que hay un modelo para la función lineal que será la nueva herramienta, es más importante que entregar a los estudiantes el modelo de función lineal cuya estructura es y = m x + b de manera directa, en una clase magistral.
Discusión interactiva y comunicativa hasta la clausura o cierre de la clase
A modo de ejemplo, se hará una descripción de las acciones que debe hacer un docente, específicamente, durante los momentos de la clase denominados discusión interactiva y el cierre.
El profesor usa la pizarra completa con la tabla 1 y el gráfico 1, durante la discusión de la solución del problema planteado. Aquí el estudiante asume un nuevo rol, debido a que, con su trabajo en grupo y posteriormente al compartir las respuestas en el plenario, participa de manera activa en su aprendizaje. Por tanto, se es coherente con las ideas de Piaget, debido a que se permite que el estudiante construya los conocimientos o participe de esa construcción. Asimismo, las ideas socioculturalistas se presentan nuevamente, porque se requiere trabajo colectivo y la interacción con el entorno a través de un problema.
Particularmente, el profesor, para el cierre, puede efectuar las acciones a continuación:
1)Agregar dos columnas a la tabla 1, las cuales debe construir con ayuda de los estudiantes.
|
Descomposición a través de la suma |
Resumen de los datos |
|
620 + 40 + 620 |
2 x 620 + 40 |
|
620 + 40 + 620 + 620 |
3 x 620 + 40 |
|
620 + 40 + 620 + 620 + 620 |
4 x 620 + 40 |
|
620 + 40 + 620 + 620 + 620 + 620 |
5 x 620 + 40 |
|
. . |
. . |
2)Plantear la siguiente pregunta: ¿Cuál es la relación entre estas columnas?
|
Cantidad de kilómetros |
Monto por pagar |
Resumen de los datos |
|
2 |
1280 |
2 x 620 + 40 |
|
3 |
1900 |
3 x 620 + 40 |
|
4 |
2520 |
4 x 620 + 40 |
|
5 |
3140 |
5 x 620 + 40 |
|
. . |
. . |
. . |
En este momento de la clase se debe considerar que la habilidad perseguida era identificar situaciones dadas que pueden ser expresadas algebraicamente en la forma y = m x + b; por tanto, el docente debe retomar la solución que se construyó durante la etapa de “discusión interactiva y comunicativa”, para hacer un cierre coherente.
A partir de las columnas anteriores, se puede establecer que si n es la cantidad de kilómetros, se puede calcular el monto por pagar usando alguna de las siguientes dos expresiones: n x 620 + 40 o 620 x n + 40. Seguidamente, si el monto por pagar es c(n), entonces: c(n) = 620 x n + 40.
A partir de aquí, el docente puede formalizar el trabajo anterior, presentar la siguiente expresión y = m x + b, como una manera general de representar un comportamiento o modelar una situación del entorno e indicar que corresponde a una función lineal. Se debe aclarar, en este punto, que dicha habilidad y sus consecutivas pretenden nada más que la identificación, no se persigue la definición de sus partes, fórmulas para determinar la pendiente y la intersección, ni cualquier otra interpretación o abordaje tradicional de la función lineal, como lo planteaba el programa de matemáticas anterior para décimo año.
El profesor puede solicitar la verificación de que esta fórmula permite hallar directamente el monto por pagar para el servicio de taxi; por ejemplo, con la pregunta d. Finalmente, el docente indicará que c(n) = 620 x n + 40 y c(n) = n x 620 + 40 son formas equivalentes de representar la misma idea.
Cabe destacar aquí los postulados de Artigue, en los cuales se evidencia que el docente adquiere un rol protagónico, porque se demuestra el dominio de los contenidos y su manejo didáctico en el desarrollo de las lecciones.
También, existen otros elementos que se evidencian en el desarrollo de una lección con esta estructura. Según Zumbado (2015), hay una correlación entre la propuesta costarricense y las características de las lecciones japonesas, la cual tiene el siguiente formato: presentación de los problemas del día, trabajo individual de los alumnos en sus puestos, discusión de los métodos de resolución destacados y resumen del punto principal.
Es importante ampliar aquí la noción de problema, de la misma manera que la conciben los japoneses. En la propuesta del problema, también se puede iniciar con una pregunta clave para atraer el pensamiento del alumno sobre un punto específico en la lección, particularmente, al comienzo, para probar o promover la comprensión del reto o el trabajo por realizar (Zumbado, 2015).
Asimismo, el modelo japonés indica que el profesor debe movilizarse por el aula, observando las actividades de manera silenciosa, evaluando el progreso de la resolución del problema y recolectando ideas sobre las distintas maneras en que los alumnos abordaron el problema. Esto coincide con las indicaciones del MEP sobre la forma de realizar la mediación durante “el trabajo estudiantil independiente”, con acciones precisas que intervengan durante el bloqueo de los estudiantes y recolecten información para efectuar el cierre o clausura, sin caer en el efecto Topaze. Esta última noción proviene de la didáctica francesa y señala que el docente debe tener cuidado al aplicar una técnica interrogativa, porque puede ocasionar una actitud de adivinación en los estudiantes o caer en el error de sugerir las respuestas (Zumbado, 2015).
El MEP (2012) asume también de la OCDE (2005) la noción de competencia matemática, las áreas del conocimiento y la inclusión de los procesos matemáticos, sin embargo, no se incorporan de manera textual. Para efectos de las tendencias didácticas, se considera la competencia matemática como un conjunto de capacidades para aplicar, formular, emplear, interpretar, analizar, razonar y comunicar, de manera eficiente, ideas matemáticas en el contexto. Se persigue que las personas puedan reconocer la importancia y utilidad de las matemáticas para poder, a su vez, tomar decisiones fundamentadas (MEP, 2012). Estas ideas son operacionalizadas en el estilo organizativo de la lección, cuando se propone iniciar con el planteo de un problema que de manera implícita conlleva las acciones aquí descritas.
Ventajas de las tendencias pedagógicas y didácticas descritas
A continuación, se presentarán algunas ventajas de las tendencias pedagógicas y didácticas como un conjunto.
Entre las ventajas que presentan las tendencias encontradas en los programas de matemáticas están la sólida historia de la cada una de ellas y la amplia investigación que se ha realizado a su alrededor. Todas se ubican en el naturalismo, corriente filosófica que plantea la naturaleza como principio de todas las acciones reales (Chávez, Deler y Suárez, 2009); esto es coherente con la resolución de problemas, porque en el contexto es donde se generan los retos que la humanidad ha necesitado superar. El constructivismo, socioculturalismo y pragmatismo realista propician las condiciones para enfrentarse a la naturaleza y ocasionar en el estudiante, de manera natural, la necesidad de tomar acciones y, por tanto, provocar un rol activo.
Asimismo, todas las tendencias didácticas se ubican en la didáctica cognitivista que está bajo la misma corriente filosófica. Según Chávez, Deler y Suárez (2009), sus orígenes se encuentran en el pragmatismo y el positivismo, pero, en la actualidad, se han superado esas visiones; en particular, en los programas oficiales costarricenses se incluyen, desde una perspectiva más profunda y específica, orientadas hacia las matemáticas con los aportes de la experiencia japonesa, francesa, norteamericana y de Freudenthal, concretamente.
Consideraciones finales
Se puede establecer que el paradigma que ampara los programas de matemáticas (MEP, 2012) es emergente, será nombrado como Aproximación integral para el aprendizaje de las matemáticas (AIM) y agrupa las siguientes tendencias pedagógicas:
•constructivismo (Piaget),
•socioculturalismo (Vygosky-Kant) y
•pragmatismo realista (Cobb, 1994).
Además, las tendencias didácticas vinculadas corresponden a
•ideas de la OECD en el marco teórico de las pruebas PISA;
•los planteamientos teóricos de la corriente de educación matemática realista (EMR) de H. Freudenthal (1973, 1983, 1991);
•la experiencia de Japón, y a
•algunos resultados de investigación de la escuela de didáctica de las matemáticas en Francia (MEP, 2012, p. 499).
Es posible encontrar evidencias, al plantear una clase de acuerdo con el estilo para la organización de las lecciones propuesto por el MEP (2012), de la presencia e impacto que cada tendencia pedagógica y didáctica señala. Asimismo, la sólida fundamentación de las tendencias seleccionadas ofrece un respaldo teórico e histórico que permite depositar la confianza en la propuesta metodológica.
Se debe indicar que, aunque son evidentes tres de los cinco ejes disciplinares, “la resolución de problemas como estrategia metodológica principal”, “la contextualización activa como un componente pedagógico especial” y “la potenciación de actitudes y creencias positivas en torno a las matemáticas” (MEP, 2012, p. 17), es posible establecer una correlación con los otros dos: “el uso inteligente y visionario de tecnologías digitales” y “el uso de la historia de las matemáticas” (MEP, 2012, p. 17). Estos últimos se pueden emplear como herramientas de un plan de lección y con ellos aumentar su dinamismo.
Finalmente, la resolución de problemas, propuesta como estrategia metodológica principal, permite la construcción del conocimiento, a través de un andamiaje apoyado por una comunidad de iguales, donde el contexto ofrece el contacto con la realidad y dota al aprendizaje de las matemáticas de un sentimiento de utilidad; donde el docente es gestor, supervisor y responsable de la culminación del acto educativo.
Sin embargo, el reto para el docente queda manifiesto, debido a que el diseño o la selección de un problema que favorezca la presencia de todos los componentes teóricos expuestos es una tarea compleja, que requiere del apoyo de las universidades, cuando se participa de la formación de futuros educadores matemáticos. Respecto a los docentes en ejercicio, se requiere el apoyo de asesores nacionales y asesores pedagógicos del área, así como el trabajo en equipo de los departamentos de matemáticas institucionales y la autocapacitación, como una muestra de responsabilidad de las funciones que se desempeñan en el aula.
El apoyo ministerial y de la academia en general debe continuar, con el objetivo de favorecer el desarrollo de destrezas en el personal docente –en cuanto al manejo de la estrategia metodológica (Ruiz, 2013)–, así como de la construcción y evaluación de problemas como recurso didáctico para el desarrollo de dicha estrategia en cada área del currículo con el objetivo de favorecer la competencia matemática.
Referencias
Bishop, A. (1999). Enculturación matemática. La educación matemática desde una perspectiva cultural. Barcelona: Editorial Paidós. Recuperado de https://maestriamatematicaipc.wikispaces.com/file/view/Enculturación+Matemática.pdf
Chávez, J.; Deler, G. y Suárez, A. (2009). Principales corrientes y tendencia a inicios del siglo XXI de la pedagogía y de la didáctica. Dirección Cubana. Ministerio de Educación.
Espinoza, J. y Zumbado, M. (2015). Planes piloto en la implementación de nuevos programas de Matemáticas. Cuadernos de Investigación y Formación de Educación Matemática, 10(13), 133-142. Recuperado de https://revistas.ucr.ac.cr/index.php/cifem/article/view/19149/19203
Gravemeijer, K. y Teruel, J. (2000). Hans Freudenthal: a mathematician on didactics and curriculum theory. J. Currículo Studies, 32(6), 777-796. Traducción: Norma Saggesse, Fernanda Gallego y Ana Bressan. Recuperado de https://www.researchgate.net/publication/241866337_HANS_FREUDENTHAL_un_matematico_en_Didactica_y_teoria_curricular
Ministerio de Educación Pública [MEP]. (2012). Programas de estudio de Matemáticas para la Educación General Básica y el Ciclo Diversificado. San José, Costa Rica: autor. Recuperado de http://www.mep.go.cr/sites/default/files/programadeestudio/programas/matematica.pdf
Ministerio de Educación Pública [MEP]. (2017). Política Educativa. La persona: centro del proceso educativo y sujeto transformador de la sociedad. San José, Costa Rica: autor. Recuperado de http://www.mep.go.cr/sites/default/files/page/adjuntos/politicaeducativa.pdf
Proyecto Reforma de la Educación Matemática en Costa Rica. (2015). Enfoque_programas_CR (2). [Video]. Recuperado de https://www.youtube.com/watch?v=GkAYX1I3jkY
Ruiz, A. (2013). La reforma de la Educación Matemática en Costa Rica. Perspectiva de la praxis. Cuaderno de Investigación y Formación en Educación Matemática, 8(n.º especial), 93-100. Recuperado de https://revistas.ucr.ac.cr/index.php/cifem/article/view/11125/10602
Soto, J. y Bernardini, A. (2007). La educación actual en sus fuentes filosóficas. San José, Costa Rica: Editorial Universidad Estatal a Distancia.
UNED, ECE, Cátedra de Didáctica de la Matemática (2017). Orientación Académica. Asignatura: 03058 Currículo en la Educación Matemática. San José, Costa Rica: autor.
Zumbado, M. (2015). A propósito de la introducción de la función logarítmica. Una correlación entre la clase “japonesa” y el currículo costarricense de Matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 10(13), 215-222. Recuperado de https://revistas.ucr.ac.cr/index.php/cifem/article/view/19159/19215
Evidencias sobre algunas tendencias pedagógicas y didácticas presentes en los programas de estudio de matemáticas costarricense (Marianela Zumbado-Castro) porRevista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported licence.
