| ISSN Electrónico: 2215-3470 DOI: http://dx.doi.org/10.15359/ru.34-1.5 |
UNICIENCIA Vol. 34, N° 1. Enero-Junio, 2020 URL: www.revistas.una.ac.cr/uniciencia Correo electrónico: revistauniciencia@una.cr |
 |
Las actitudes hacia la matemática, el desarrollo social, el nivel educativo de la madre y la autoeficacia como factores asociados al rendimiento académico en matemática
Impacts of attitudes, social development, mother’s educational level and self-efficacy on academic achievement in mathematics
As atitudes relacionadas à matemática, o desenvolvimento social, a escolaridade materna e autoeficácia como fatores associados ao desempenho acadêmico na matemática
José Andrey Zamora-Araya
jzamo@una.ac.cr
Escuela de Matemática
Universidad Nacional,
Heredia, Costa Rica.
Orcid: http://orcid.org/0000-0001-6050-5850
Received: 31/jan/2019 • Accepted: 27/may/2019 • Published: 31/jan/2020
|
Resumen El documento trata sobre la problemática del bajo rendimiento académico en matemática (RAM) y, como objetivo principal, analiza de qué manera se relaciona este con las actitudes hacia la materia, la autoeficacia percibida, el desarrollo social y el nivel educativo. Participaron 197 estudiantes de 7.o, 8.o y 9.o grado de colegio con edades entre los 13 y 16 años. El estudio es de tipo correlacional y se utilizaron las técnicas de análisis factorial exploratorio y regresión múltiple, para determinar la asociación entre los constructos. Tales tácticas confirman la importancia de que los estudiantes tengan seguridad en sí mismos cuando realizan tareas matemáticas, lo que se refleja en los coeficientes significativos para las dimensiones de confianza (p = 0.001) y experiencia de maestría (p < 0.001), pero no así el nivel educativo de la madre. También, se obtuvieron resultados inesperados con respecto al desarrollo social y algunas dimensiones de la escala de actitudes hacia la matemática; sin embargo, se reafirma lo fundamental de estos constructos y la autoeficacia en el RAM, por lo que se recomienda ampliar la investigación sobre dichas variables. Palabras clave: enseñanza secundaria; rendimiento escolar; análisis factorial; autoconcepto. Abstract The document addresses the problem of low academic performance in Mathematics (LPM). Its principal objective is to analyze how academic performance relates to attitudes towards this subject, perceptions of self-efficacy, social development and the educational level of students’ mothers. One hundred and ninety-seven (197) students in the 7th, 8th and 9th grades of middle and high school, between 13 and 16 years old, participated in the study. This correlational study used techniques of exploratory factor analysis and multiple regression to determine the association between the constructs. The results confirm the importance of students trusting in their abilities when performing mathematical tasks, which is reflected on the significant coefficients for the dimensions of confidence (p = 0.001) and master experience (p <0.001), but the educational level of the mother did not have a significant effect on learning outcomes. Unexpected results were also found with respect to social development and some dimensions of the scale of attitudes towards mathematics, but the impacts of these constructs and self-efficacy on LPM were verified. Based on these findings, it is recommended to carry out further research on the effects of these factors. Keywords: secondary education; academic performance; factor analysis; self-concept. Resumo O artigo aborda a dificuldade da aprendizagem em matemática (DAM) e analisa, como principal objetivo, de que maneira este rendimento está relacionado com as atitudes alusivas à matéria, a autoeficácia percebida, o desenvolvimento social e o nível acadêmico. Participaram 197 estudantes do 7º, 8º e 9º ano do colégio com idades entre 13 e 16 anos. O estudo é do tipo de correlação e foram utilizadas as técnicas de análise fatorial exploratória e de regressão múltipla para determinar a associação entre os construtos. Tais táticas confirmam a importância de os estudantes terem autoconfiança quando realizam tarefas matemáticas, o que se reflete nos coeficientes significativos para as dimensões de confiança (p = 0,001) e a experiência docente (p <0,001), mas não o nível educacional da mãe. Além disso, foram obtidos resultados inesperados relacionados ao desenvolvimento social e algumas dimensões da escala de atitudes com relação à matemática; no entanto, reafirma-se o quão fundamental são estes construtos e a autoeficácia na DAM, sendo aconselhável, portanto, ampliar a pesquisa sobre essas variáveis. Palavras-chave: ensino fundamental; rendimento escolar; análise fatorial; autoconceito. |
Introducción
El bajo rendimiento académico en matemática (RAM) es un problema que tienen muchos sistemas educativos en el mundo, como lo demuestran los resultados de las pruebas del Programa para la Evaluación Internacional de los Alumnos (PISA, por sus siglas en inglés), en las cuales en el 2012 —para todos los países participantes— una tercera parte de los estudiantes no alcanza el nivel básico de competencias matemáticas 2. Es decir, el alumnado únicamente es capaz de extraer información relevante de una sola fuente y utilizar procedimientos básicos, con el propósito de resolver, por medio de fórmulas o algoritmos, problemas que tengan números enteros (OCDE, 2016).
Para Costa Rica, que está intentando ingresar a la Organización para la Cooperación y el Desarrollo Económico (OCDE), los resultados obtenidos en matemática, según el informe PISA 2015, evidencian un bajo rendimiento, pues el promedio en las pruebas pasó de 406 a 400 puntos. A pesar de ello, el país ocupa el tercer puesto en América Latina, detrás de Chile y Uruguay, pero con rendimientos muy pobres tanto en matemática como en ciencias (OCDE, 2016).
Diversas razones inciden en el bajo aprovechamiento en matemática, entre ellas, pueden citarse la falta de motivación, el clima educativo del hogar, condiciones sociales, económicas y personales de los estudiantes, así como factores de tipo cognitivo (Broadbent y Poon, 2015; Bullón, Campos, Castaño, Léon y Polo, 2017; Chong y Guadalupe, 2017). Otros de los factores, cuya relación con el rendimiento académico han mostrado ser importantes, son la autoeficacia percibida y la actitud hacia la disciplina, en este caso matemática, así como el contexto socioeconómico y el nivel de educación de los padres (Bandura, 1977, 1987, 1993; Da Cuña, Gutiérrez, Barón y Labajos, 2014).
El presente estudio pretende explicar el RAM en una muestra de estudiantes de educación secundaria, usando como covariables el nivel educativo de la madre (NEM) y escalas que permiten medir las actitudes hacia la asignatura, autoeficacia y un constructo denominado desarrollo social como una medida de bienestar social que se ha utilizado en estudios económicos, pero muy poco en relación con el rendimiento escolar (Gómez y Barrero, 2016). Así pues, el objetivo principal del trabajo es determinar en qué grado influyen los constructos de actitudes hacia la matemática, la autoeficacia, el desarrollo social y el NEM en el RAM. Para ello, se plantea como objetivos específicos determinar la magnitud de la correlación entre los constructos descritos y el NEM con el RAM, medido a través de las calificaciones en el último trimestre del año.
El documento se estructura de la siguiente forma: a) una primera parte de referentes teóricos, en la cual se describen los constructos usados para la regresión múltiple; b) una sección de metodología, en la que se describen la población, los criterios de inclusión y exclusión de la muestra, el tipo de muestreo y las técnicas multivariadas que se utilizan para efectuar los análisis; c) un apartado de resultados que muestran los análisis de los modelos utilizados; d) una discusión de los resultados; y e) un último segmento de conclusiones.
Referentes teóricos
Rendimiento académico
El rendimiento académico es un fenómeno multifactorial y complejo. La dificultad inicia con su definición, pues los términos aptitud escolar, desempeño académico y rendimiento escolar se han trabajado como sinónimos en la práctica educativa (Edel, 2003).
Existen varios autores quienes han definido el rendimiento académico, por ejemplo, para Martínez (2008) es “el producto que da el alumnado en los centros de enseñanza y que habitualmente se expresa a través de las calificaciones escolares” (p. 34). Por su parte, Camarena, Chavez y Gómez (1985) se refieren al concepto como:
una expresión valorativa particular del proceso educativo que se da en el marco de la institución escolar. Este proceso, al incorporar el conjunto de relaciones pedagógicas y sociales que inciden en la institución, condiciona al rendimiento, ya que éste esta subordinado a todas las variaciones, contradicciones, cambios y transformaciones del mismo proceso. (p 4)
Por otro lado, existen factores que pueden denominarse como internos y que están relacionados con autoestima, autoconcepto, experiencia previa, actitud hacia la materia, autoeficacia percibida, motivación, entre otros, que han mostrado estar asociados de manera positiva con el rendimiento académico (Honicke y Broadbent, 2016; Bandura, 1977).
También existen factores externos, como el apoyo familiar, y otros socio-económicos, como el nivel educativo de los padres y sus expectativas, considerados importantes por su relación directa con el rendimiento académico (Bullón et al., 2017; Chong y Guadalupe, 2017). En este particular, existen numerosos estudios que vinculan positivamente el nivel educativo de los padres con el buen rendimiento académico, pues se asume que a mayor cantidad de años de estudio por parte de los progenitores más será el tiempo dedicado a la supervisión de las tareas escolares de sus hijos y, por ende, a un mejor acompañamiento (Bullón et al., 2017; Da Cuña et al., 2014; Giménez y Castro, 2017)
En resumen, el rendimiento académico se ve influenciado por una gran cantidad de factores y es labor del investigador decidir cuáles de ellos utilizar para lograr sus propósitos. En este estudio, se utilizará como variable respuesta el RAM, medido por la nota promedio del último trimestre y, como variables explicativas, dimensiones de los constructos actitudes hacia la matemática, autoeficacia matemática y desarrollo social, así como el NEM. Este último ha sido considerado relevante, pues es el indicador por excelencia para medir el clima educativo del hogar y por su influencia en el desarrollo escolar del estudiante, sobre todo en los primeros años (Giménez y Castro, 2017).
Autoeficacia percibida
El constructo de autoeficacia fue introducido por Bandura (1977), padre de la teoría social cognitiva. De acuerdo con esta, la forma en que las personas interpretan los resultados de sus acciones brinda información y puede alterar su ambiente, así como las creencias de los individuos dan información (o alteran) su comportamiento futuro, es decir, la conducta de las personas es mediada por las creencias que tienen respecto de sus propias capacidades (Bandura, 1987).
De esta manera, la motivación y la conducta están reguladas por las creencias y expectativas de la gente que, según Bandura (1993), pueden ser de tres tipos.
1. Las expectativas de la situación: Los resultados se producen por eventos ambientales, sin que necesariamente medien las acciones de la persona.
2. Las expectativas de resultado: Tienen que ver con la creencia de que determinadas conductas producen determinados resultados.
3. Las expectativas de autoeficacia o autoeficacia percibida: Se ligan con la creencia de la persona de tener las capacidades suficientes para hacer correctamente una determinada tarea.
Es así, como muchos estudios han mostrado que la autoeficacia percibida se relaciona directamente con el rendimiento académico, ya que el estudiante quien se siente capaz de tener éxito en las tareas asignadas por el docente, posiblemente, lo refleje en sus calificaciones (Honicke y Broadbent, 2016; Bandura, 1977).
Por ello, se considera importante la teoría social cognitiva de Bandura, a la hora de explicar el rendimiento académico, en especial, el constructo de autoeficacia percibida. Además, este es ampliamente estudiado en el ámbito educativo y ha probado su utilidad como predictor del rendimiento académico (Bandura, 1993). Para esta investigación y con el fin de operacionalizar el constructo, se utilizará las subescalas de la escala de autoeficacia matemática elaborada por Usher y Pajares (2009), descritas en Zalazar, Aparicio, Ramírez y Garrido (2011).
Actitudes hacia la matemática
Para Martínez (2008), las actitudes son “predisposiciones o juicios valorativos o evaluativos, favorables o desfavorables, que determinan las intenciones personales de los sujetos y son capaces de influir sus comportamientos o acciones frente al objeto, sujeto o situación” (p. 244). Además, cuando se habla de actitudes, se hace alusión a lo que se conoce como dominio afectivo, el cual es definido por McLeod (1989) como “un amplio rango de sentimientos y humores que generalmente son considerados como algo diferente a la pura cognición” (p. 245). De la acepción anterior, se infiere que, al hablar de actitudes, lo más importante son las creencias, emociones y sentimientos del sujeto cognoscente hacia el objeto que conoce. En cuanto a las actitudes en el campo matemático, es decir, si el objeto de estudio es la matemática, según Cárdenas (2008), existen dos grandes categorías.
1. Actitudes hacia la matemática: Tratan sobre el gusto, aprecio o interés que una persona siente por la asignatura y su aprendizaje. Se pueden referir a comportamientos hacia
•la matemática y los matemáticos (aspectos sociales);
•el interés por el trabajo matemático, científico;
•la matemática como asignatura;
•determinadas partes de la matemática;
•los métodos de enseñanza.
2. Actitudes matemáticas: A diferencias de las primeras, dan mayor importancia al componente cognitivo y se refieren a la manera en que los sujetos usan sus capacidades (como la flexibilidad de pensamiento, la apertura mental, el espíritu crítico, la objetividad, entre otras consideradas relevantes) para el quehacer matemático.
Para efectos de la presente investigación, se hará énfasis en las actitudes hacia la matemática, en particular, en aquellos aspectos referentes a lo social. Para ello, se utilizará la escala de actitudes hacia la matemática desarrollada por Fennema-Sherman y adapatada por Doepken, D. Lawsky y Padwa (1993).
Desarrollo social
El desarrollo social enfatiza la necesidad de poner en primer plano a las personas. Puede ser concebido como un cambio positivo en las condiciones de vida de los individuos que integran una sociedad, al igual que en las relaciones que tienen unos con otros o grupos y organizaciones que componen el tejido social de una nación. El concepto está directamente vinculado con el desarrollo de capital humano de un país, por lo que se enlaza con las condiciones educativas, de salud, empleo, seguridad ciudadana y se puede palpar en los niveles de desigualdad, pobreza, exclusión y vulnerabilidad, que sufren ciertas agrupaciones de la población (CEPAL, 2018).
De acuerdo con el Ministerio de Planificación Nacional y Política Pública de Costa Rica (MIDEPLAN), el desarrollo social se define como:
Proceso que busca alcanzar una mayor calidad de vida de la población, mediante una sociedad más igualitaria, participativa e inclusiva, que garantice una reducción en la brecha que existe en los niveles de bienestar que presentan los diversos grupos sociales y áreas geográficas, para lograr una integración de toda la población a la vida económica, social, política, ambiental y cultural del país, en un marco de seguridad, respeto y promoción de los derechos humanos (p .2).
A partir de él, el MIDEPLAN (2017) construyó un índice de desarrollo social (IDS) que considera las siguientes dimensiones.
Económica: Relacionada con la participación en las actividades económicas, así como en las condiciones que favorecen la inserción laboral, para lograr un ingreso que permita un nivel de vida digno.
Participación social: Referida a procesos cívicos que muestran el nivel de pertenencia y cohesión social, el cual favorece una participación activa y responsable.
Salud: Se asocia con el derecho de gozar una vida sana, para lo que se requiere acceso a servicios de salud y tener una nutrición balanceada.
Educativa: Ligada al acceso a los servicios educativos y de capacitación, que permitan un adecuado desarrollo del capital humano.
Seguridad: Vinculada con la capacidad de que las personas puedan vivir y desenvolverse en un ambiente tranquilo, sin violencia y delitos que atenten contra su integridad física.
MIDEPLAN calcula el IDS tanto en el nivel cantonal como en el distrital, con la intención de caracterizar las condiciones de vida de sus habitantes, basándose en los factores ya mencionados. La escala del IDS varía entre 0 y 100, clasificando a los distritos en zonas de desarrollo relativo; el mayor lo obtienen los distritos con puntuaciones entre 76.88 y 100. El menor desarrollo relativo se divide en tres niveles: medio (entre 62.02 y 76.87), bajo (entre 47.45 y 62. 01) y muy bajo (entre 0 y 47.44) (MIDEPLAN, 2017). Es así, como el IDS se convierte en un indicador del bienestar económico y social del estudiante y es razonable pensar que tenga una relación positiva con el rendimiento académico, pues a mayores niveles de desarrollo social se esperaría obtener mejores calificaciones. Sin embargo, este nexo no siempre es tan claro cuando se trata de RAM, como lo evidencia el estudio de Zamora-Araya (2012), el cual mostró, con estudiantes universitarios, que el IDS incluso puede tener una relación inversa con el RAM.
Con base en los constructos teóricos descritos, se establecen las siguientes hipótesis: a) el RAM está directamente correlacionado con las actitudes hacia la matemática, de tal manera que a mayores actitudes hacia la asignatura mayor rendimiento académico; b) el RAM aumenta conforme incrementa el nivel educativo de los padres de familia; c) el RAM sube conforme se eleva el nivel de autoeficacia matemática percibida por el estudiante; y d) entre mayor sea el nivel de desarrollo social del estudiante mayor será su RAM.
El contraste de las anteriores hipótesis se realizará por medio de un diseño correlacional, utilizando la técnica multivariada de regresión múltiple, que permitirá determinar en qué medida se asocian las dimensiones expresadas, por medio de los indicadores que forman las variables explicativas del modelo. Con ello, se tomará conciencia sobre la importancia de algunas características individuales y familiares del estudiante.
Metodología
Diseño de la investigación
De acuerdo con Hernández, Fernández y Batista (2014), esta investigación es de tipo no experimental, dado que no se pretende realizar manipulación directa de las variables. Como se recolectaron datos en un solo momento durante el trabajo de campo, el estudio es transversal y, puesto que interesa conocer la relación entre las variables establecidas en cada una de las hipótesis con el RAM, también es correlacional (las variables se observaron en su contexto natural, para determinar la relación existente entre ellas). Con tal finalidad, se aplicó un cuestionario autoadministrado, descrito en detalle en las siguientes secciones, que proporcionó información sobre variables familiares y sociodemográficas de los estudiantes, así como datos mediante escalas de los constructos actitudes hacia la matemática y autoeficacia matemática.
Participantes
Los sujetos participantes del estudio son estudiantes del tercer ciclo de educación general básica (7.o, 8.o y 9.o año) de un colegio técnico profesional de la región de Heredia. Sus edades oscilan entre los 13 y 16 años y todos pasaron por un proceso de admisión, que incluía la realización de pruebas escritas en las áreas de matemática, español, estudios sociales e inglés, para poder matricularse en la institución.
Los criterios de inclusión fueron a) asistencia durante el período de recolección de la información y b) consentimiento para participar en el estudio. Como criterios de exclusión se consideraron a) que el estudiante no estuviera en la condición de “arrastre” en la asignatura de matemática y b) que tuviera nota de matemática reportada en el tercer trimestre.
Las principales características referentes a quienes participaron se describen en la tabla 1. En ella, se puede apreciar que las mujeres superan, ligeramente, en número a los hombres; que, en su mayoría, los estudiantes nunca han reprobado ningún año o han tenido que realizar examen de convocatoria en la asignatura de matemática, lo que posiblemente se deba al proceso de selección realizado por la institución. Además, hay un bajo porcentaje de alumnos becados, lo cual podría estar relacionado con el nivel económico y de educación de los padres.
Tabla 1
Medidas descriptivas para las principales variables cualitativas. N = 197
|
Variable |
Frecuencia |
Porcentaje |
Variable |
Frecuencia |
Porcentaje |
|
Sexo |
Ha reprobado anteriormente |
||||
|
Hombre |
94 |
47.72 |
SÍ |
6 |
3.05 |
|
Mujer |
103 |
52.28 |
NO |
191 |
96.95 |
|
Tenencia de beca |
Ha tenido que presentar matemática |
||||
|
Sí |
46 |
23.35 |
Sí |
5 |
2.54 |
|
No |
151 |
76.65 |
No |
192 |
97.46 |
|
Nivel de estudios del padre |
Nivel de estudios de la madre |
||||
|
Primaria |
23 |
11.68 |
Primaria |
26 |
13.2 |
|
Secundaria |
105 |
53.3 |
Secundaria |
89 |
45.18 |
|
Universidad |
69 |
35.03 |
Universidad |
82 |
41.62 |
Nota: Fuente propia de la investigación.
Procedimientos de muestreo
Se pidió permiso a la dirección del centro educativo, a los padres de familia, mediante un consentimiento informado, y a los profesores de matemática, para poder aplicar un cuestionario autoadministrado; ellos accedieron. La muestra estuvo constituida por un total de 197 estudiantes, que fueron seleccionados por medio de un muestreo de conglomerados, siete grupos de un total de 10, correspondientes a los niveles de sétimo, octavo y noveno año. Se les solicitó su autorización para completar el instrumento y a aquellos que lo hicieron se les garantizó la anonimidad de los datos.
Descripción del instrumento utilizado
El cuestionario utilizado consta de dos partes. La primera de ellas recaba información general sobre el estudiantado, como nombre, sección, sexo, entre otras variables de índole académica y familiar. La segunda parte se refiera a tres escalas para medir los constructos de actitudes hacia la matemática y autoeficacia matemática. La primera es la escala de actitudes de Fennema-Sherman, adaptada para actitudes hacia la matemática, que puede encontrarse en el artículo de Doepken, Lawsky y Padwa (1993); las otras dos son subescalas de la escala de autoeficacia matemática elaborada por Usher y Pajares (2009). Todos los ítems están construidos por una escala tipo Likert de cinco opciones, es decir, la puntuación varía entre uno y cinco; el valor uno es el que corresponde al menor grado, de acuerdo con la afirmación propuesta (completamente en desacuerdo), y cinco, el de mayor grado (completamente de acuerdo).
La escala de actitudes está compuesta por 24 ítems que contienen frases referentes a la actitud de los estudiantes respecto a la matemática. Asimismo, las subescalas de autoeficacia matemática denominadas persuasión social y experiencia de maestría, que fueron adaptadas y traducidas al español por Zalazar et al. (2011), constan de seis reactivos cada una y se obtuvieron valores de alfa de Cronbach de 0.90 y 0.83, respectivamente. El número de valores faltantes, para cada uno de los 36 reactivos, osciló entre cero y cuatro; fueron imputados, asignando la media del reactivo.
A la escala de actitudes se le aplicó un análisis factorial exploratorio (AFE), que dio como resultado la determinación de tres dimensiones: utilidad, confianza y seguridad. Sus índices de confiabilidad fueron 0.88, 0.89 y 0.76, respectivamente, y son considerados aceptables para los objetivos del estudio.
Resultados
Para la escala de actitudes hacia la matemática, se realizó un análisis AFE y se aplicó la prueba de homogeneidad de Bartlett (p = 0.000) junto con la de Kaiser-Meyer-Olkin (p = 0.89), las cuales comprobaron la pertinencia de llevar a cabo un AFE.
Empleando el criterio de Kaiser, el AFE sugiere la presencia de tres factores (ver gráfica 1). La tabla 2 muestra los reactivos para cada factor: utilidad, confianza y seguridad. En total, los tres factores explican un 47, 3 % de la variancia total y las correlaciones entre ellos oscilan entre 28 % y 39 %. Con el fin de constrastar las hipótesis, se plantea un análisis de regresión múltiple que incorpora dichos factores, las dos subescalas de autoeficacia y el NEM, como predictores, al igual que el RAM, como variable dependiente.
Es así como se analizaron varios modelos hasta llegar a uno final, que prescinde de los predictores NEM, utilidad y persuasión, cuyo porcentaje de varianza explicada es 29,84 % (ver tabla 3). En el modelo seleccionado, todos los predictores son significativos al 5 % y se confirman algunas de las hipótesis de trabajo, pero también este arroja resultados no esperados que se discutirán en la siguiente sección.
Gráfica 1
Gráfico de sedimentación para la escala de actitudes hacia la matemática
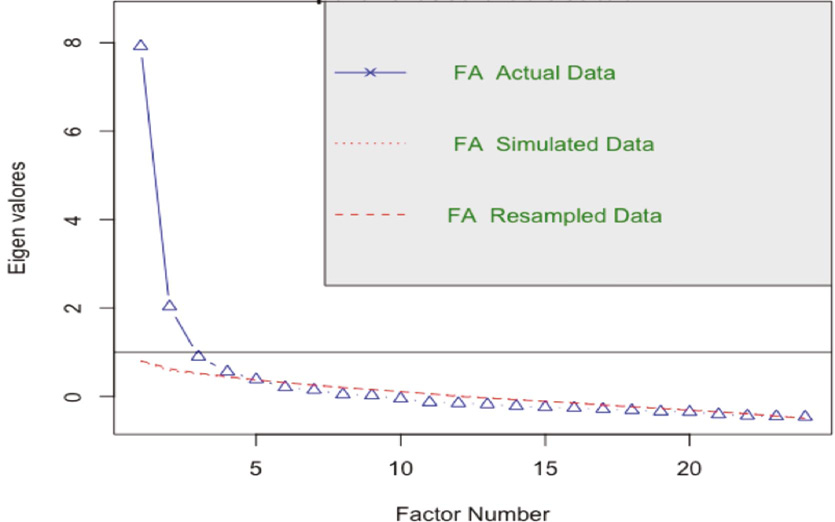
Nota: Fuente propia del estudio.
Tabla 2
Reactivos para cada factor de la escala de actitudes hacia la matemática
|
Factor 1 |
Factor 2 |
Factor 3 |
|
1. Estoy seguro/a de que puedo aprender matemática. |
3. No creo que pueda dominar la matemática avanzada. |
7. Estoy seguro/a de mí mismo/a cuando resuelvo problemas de mate. |
|
2. Tener dominio sobre la matemática me ayudará a ganarme la vida. |
5. La matemática es difícil para mí. |
13. Creo que podría resolver problemas de mate complejos. |
|
4. La matemática no va a ser importante para desempeñarme bien en la carrera que yo quiero. |
8. No espero usar mucha matemática cuando salga del cole o de la U. |
17. Puedo sacar buenas notas en mate. |
|
6. Voy a necesitar la matemática para mi futuro trabajo. |
10. No soy el tipo de persona a la que le va bien en mate. |
21. Estoy seguro/a de que podría resolver operaciones matemáticas avanzadas. |
|
9. Mate es una materia necesaria. |
12. En lo que me va peor es en mate. |
|
|
11. Estudiar mucho mate es una pérdida de tiempo. |
16. Me van bien en casi todas las materias, menos en mate. |
|
|
14. En el futuro, voy a utilizar la matemática en muchos sentidos. |
19. Sé que puedo ser bueno/a en matemática. |
|
|
15. Veo la matemática como algo que no voy a utilizar muy a menudo cuando salga del cole o de la U. |
23. No soy bueno/a en matemática. |
|
|
18. Voy a necesitar una buena comprensión de la matemática para mi trabajo en el futuro. |
||
|
20. Dominar la matemática no es importante para mi futuro. |
||
|
22. En mi vida, la matemática no es importante. |
||
|
24. Estudio matemática porque sé lo útil que es. |
Nota: Fuente propia de la investigación.
Tabla 3
Modelo de regresión múltiple final para el rendimiento académico en matemática. N= 197
|
Coeficientes |
Estimación |
Error estándar |
Valor t |
Valor p |
|
(Intercept) |
88.378 |
7.076 |
12.490 |
2.00E-16 |
|
Confianza |
0.302 |
0.115 |
2.6330 |
0.001 |
|
Seguridad |
-0.684 |
0.178 |
-3.849 |
1.61E-04 |
|
Experiencia de maestría |
0.956 |
0.172 |
5.569 |
8.55E-08 |
|
IDS |
-0.179 |
0.083 |
-2.170 |
0.031 |
Nota: Fuente propia del estudio.
Discusión de resultados
Los resultados de la regresión múltiple apoyan, parcialmente, la hipótesis referente a la relación directa y significativa que tienen la actitudes hacia la matemática, representada en la dimensión de confianza con el RAM, al igual que la autoeficacia en la subescala de denominada experiencia de maestría. En el caso de la confianza, el incremento de un punto en la escala aumenta en 0.30 la calificación en la asignatura de matemática y en cuanto a la experiencia de maestría, cada incremento de un punto representa un aumento de 0.95 en el RAM, siendo ambas significativas en el modelo final (p = 0.01 y p < 0.001, respectivamente). Esto es totalmente consecuente con otras investigaciones realizadas, hecho que reafirma la importancia de la autoeficacia percibida y las actitudes hacia la matemática como predictores del rendimiento académico (Bandura, 1977, 1987, 1993; Honicke y Broadbent, 2016; Zalazar et al., 2011).
No obstante, se dice que las hipótesis se cumplen de manera parcial, pues, en el modelo originalmente propuesto, la subescala de persuasión social (autoeficacia) y la dimensión de utilidad (actitudes hacia la matemática) poseen coeficientes que no resultaron significativos (p = 0.477 y p = 0.253, respectivamente).
Con respecto a la persuasión social, su pobre desempeño como predictor se puede deber a que las preguntas se asocian con reconocimientos a los estudiantes, por parte de otras personas como familiares, compañeros o profesores, sobre su RAM y, posiblemente, este tipo de frases no sean muy comunes o no tengan tanta relevancia en este contexto educativo. De hecho, la media de los reactivos en esta escala oscila entre 2.5 y 3.1 puntos, por lo que las respuestas de los participantes se ubican entre las categorías de ligeramente en desacuerdo y ni en desacuerdo ni en acuerdo. Esto podría explicar la baja magnitud del coeficiente.
En la escala de utilidad, la media de los ítems varía entre 3.4 y 4.4, denotando un acuerdo generalizado entre los estudiantes, acerca de la funcionalidad que tiene la matemática, independientemente de su RAM. Esto puede provocar que sus puntuaciones no correlacionen significativamente, pues, los estudiantes tanto con alto como con bajo rendimiento consideran útil la asignatura.
También, se descartó del modelo original la variable NEM con valores de p, en relación con las categorías de secundaria y universidad (tomando como referencia primaria), de 0.296 y 0.475. Los tamaños de efecto son muy bajos (0.049 y 0.006 respectivamente), por lo que las diferencias en el RAM, según el NEM, no son relevantes, como lo muestran el valor de las medias 83.509, 84.593 y 84.259 para primaria, secundaria y universidad en el RAM, respectivamente.
Lo anterior puede deberse a la forma en que se compone la población, pues, cerca de un 42 % de las madres posee estudios universitarios y tan solo un 13 % tiene, como su mayor nivel educativo, estudios de educación primaria, hecho que no permite captar las diferencias relacionadas con el nivel de instrucción de los padres. Esto también se ve reflejado en el IDS, dado que, en la muestra, solo hay estudiantes con desarrollo social de nivel medio o alto.
El IDS resultó significativo (p = 0.031), pero con signo negativo. Con ello se interpreta que un aumento de un punto en el índice corresponde a una reducción de 0.179 en el RAM, lo que es contrario a la hipótesis inicialmente formulada.
Esta relación inversa entre el IDS y el RAM puede deberse a varias situaciones. Primero, el IDS está compuesto por cinco dimensiones (seguridad, salud, educación, participación social y economía); es posible que no todas aporten en la misma magnitud y dirección a la hora de explicar el RAM y quizá sería mejor considerar los factores con más relación con el constructo, como los educativos y económicos, en lugar de tomar el índice en su totalidad, para lo cual deberían realizarse estudios que profundicen en ello. Una segunda consideración se refiere a cómo está compuesta la población en estudio, en cuanto a su nivel socioeconómico y al rango profesional de los padres, pues la mayoría son de estrato medio o alto, de acuerdo con la clasificación propuesta por MIDEPLAN (2017); es decir, no hay estudiantes con niveles bajos o muy bajos de IDS, en el que se podría apreciar mejor la relación entre el índice y rendimiento académico.
En lo referente a la dimensión de seguridad, a pesar de resultar significativa en el modelo final (p = 0.04), su coeficiente posee una dirección contraria a la esperada, ya que, por cada aumento de un punto en la escala de seguridad, el RAM disminuye en 0.68. Al respecto se conversó con los profesores y orientadoras de la institución y una explicación plausible para este fenómeno es que el personal docente ha estado motivando al estudiantado con bajo rendimiento, para instarlo a superar sus notas. Se le menciona que es capaz de salir adelante y que es posible recuperar las bajas notas obtenidas en períodos anteriores, además de brindarles apoyos académicos como planes remediales. Puesto que la dimensión de seguridad refiere a preguntas relativas a la capacidad para poder afrontar las tareas matemáticas (ver tabla 2), esto podría esclarecer, al menos en parte, el comportamiento en el análisis de regresión; no obstante, el resultado es contradictorio a lo esperado y futuras investigaciones deberían profundizar en él.
Conclusiones
El análisis realizado confirma la importancia de que los estudiantes tengan confianza en sí mismos, cuando realizan tareas matemáticas y esto se ve reflejado en su RAM. Sin embargo, los datos también muestran resultados inesperados que no avalan algunos planteamientos iniciales. Por ejemplo, la relación entre el RAM y el IDS esperada directa resultó inversa, muy posiblemente por el contexto educativo (clase media, media-alta) donde se desarrolló el estudio, pues las características de la población pueden influir en los resultados, debido a los procesos de selección que aplica la institución. Esta, junto con el ambiente institucional, puede explicar —al menos en parte— los datos obtenidos.
Asimismo, los coeficientes de las dimensiones de utilidad arrojadas por el AFE y la seguridad también fueron sorpresivas, pues, aunque la utilidad siguió la dirección esperada, no resultó significativa en su relación con el rendimiento y esto podría deberse a un concenso generalizado sobre la utilidad de la matemática, sea que “me vaya bien o mal en las pruebas”, lo que resta su capacidad como predictor de rendimiento. Por su parte, la seguridad no solo quedó fuera del modelo final, sino que su coeficiente tiene una relación inversa con el RAM, lo cual va en contra de lo planteado inicialmente. Una razón para este resultado puede estar enlazada a la población, ya que la institución selecciona a los estudiantes con base en un examen de admisión, lo que, aunado al trabajo sobre autoestima del departamento de orientación y la labor docente con planes remediales, más otros apoyos, podría incidir en la relación inversa detectada entre seguridad y RAM.
Para el caso de la dimensión de la ansiedad denominada persuasión social, su no inclusión en el modelo final posiblemente se deba a que las frases que componen la escala se pueden interpretar como halagos o expresiones, los cuales quizás puedan denotar cierta arrogancia e inhiben a los estudiantes a brindar una respuesta sincera, por ejemplo: “los adultos de mi familia me dicen que soy un buen estudiante en matemática” o “he sido elogiado por mi habilidad en matemática”.
Finalmente, el estudio abre la posibilidad y la necesidad de continuar con investigaciones relativas a las actitudes hacia la matemática, la autoeficacia y el desarrollo social, pero en diferentes contextos o con mayor alcance, como en los niveles regional o nacional, que involucren mayor número y diversidad de instituciones. También se aconseja utilizar otras metodologías, como el análisis factorial confirmatorio, modelos de ecuaciones estructurales, estudios cualitativos o mixtos, que puedan analizar, con mayor profundidad, la relación entre los constructos.
Referencias
Bandura, A. (1977). Self-efficacy: toward a unifying theory of behavioral change. Psychological review, 84(2), 191-215. doi: http://dx.doi.org/10.1037/0033-295X.84.2.191
Bandura, A. (1987). Pensamiento y acción: Fundamentos sociales. Barcelona, España: Martínez Roca.
Bandura, A. (1993). Perceived self-efficacy in cognitive development and functioning. Educational psychologist, 28(2), 117-148. doi: http://dx.doi.org/10.1207/s15326985ep2802_3
Broadbent, J. y Poon, W. L. (2015). Self-regulated learning strategies & academic achievement in online higher education learning environments: A systematic review. The Internet and Higher Education, 27, 1-13. doi: http://dx.doi.org/10.1016/j.iheduc.2015.04.007
Bullón, F. F.; Campos, M. M.; Castaño, E. F.; Léon del Barco, B. L. y Polo del Río, M. I. P. (2017). Análisis del rendimiento académico de los alumnos de Educación Secundaria Obligatoria según las variables familiares. Educación XXI, 20(1), 209-232. doi: https://doi.org/10.5944/educxx1.17509
Camarena, R.; Chávez, A. M. y Gómez, J. (1985). Reflexiones en torno al rendimiento escolar y a la eficiencia terminal. Revista de la educación superior, 53(14), 3-13. Recuperado de http://publicaciones.anuies.mx/pdfs/revista/Revista53_S1A2ES.pdf
Cárdenas, C. (2008). Identificación de tipologías de actitud hacia las matemáticas en estudiantes de séptimo y octavo grados de educación primaria. Perfiles Educativos, 30(122), 94-108. Recuperado de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0185-26982008000400005&lng=es&tlng=es
CEPAL. (2018). Hacia una agenda regional de desarrollo social inclusivo: bases y propuesta inicial. Recuperado de https://repositorio.cepal.org/bitstream/handle/11362/44019/4/S1800662_es.pdf
Chong, G. y Guadalupe, E. (2017). Factores que inciden en el rendimiento académico de los estudiantes de la Universidad Politécnica del Valle de Toluca. Revista Latinoamericana de Estudios Educativos (México), 47(1), 91-108. Recuperado de http://www.redalyc.org/articulo.oa?id=27050422005
Da Cuña, I.; Gutiérrez, M.; Barón, F. J. y Labajos, M. T. (2014). Influencia del nivel educativo de los padres en el rendimiento académico, las estrategias de aprendizaje y los estilos de aprendizaje desde la perspectiva de género. Journal of Learning Styles, 7(13), 64-84. Recuperado de http://learningstyles.uvu.edu/index.php/jls/article/view/25/161
Doepken, D.; Lawsky, E. y Padwa, L. (1993). Modified fennema-sherman attitude scales. Recuperado de http://www.academia.edu/download/24153587/Modified_Fennema.docx
Edel, R. (2003). El rendimiento académico: concepto, investigación y desarrollo. REICE, 1(2), 1-15. Recuperado de http://www.redalyc.org.una.idm.oclc.org/pdf/551/55110208.pdf
Giménez, G. y Castro, G. (2017). ¿Por qué los estudiantes de colegios públicos y privados de Costa Rica obtienen distintos resultados académicos? Perfiles latinoamericanos, 25(49), 195-223. doi: https://dx.doi.org/10.18504/pl2549-009-2017
Gómez, H. S. y Barrero, M. S. R. (2016). El sector solidario como alternativa para el desarrollo social e inclusivo en el postconflicto colombiano. Cooperativismo & Desarrollo, 23(107), 53-78. Recuperado de https://revistas.ucc.edu.co/index.php/co/article/view/1250
Hernández, R.; Fernández, C. y Baptista, P. (2014). Metodología de la Investigación. México D. F.: McGraw-Hill.
Honicke, T. y Broadbent, J. (2016). The influence of academic self-efficacy on academic performance: A systematic review. Educational Research Review, 17, 63-84. doi: https://doi.org/10.1016/j.edurev.2015.11.002
Martínez, O. J. (2008). Actitudes hacia la matemática. Sapiens. Revista Universitaria de Investigación, 9(1), 237-256. Recuperado de http://www.redalyc.org.una.idm.oclc.org/pdf/410/41011135012.pdf
McLeod, D. B. (1989). Beliefs, attitudes, and emotions: New views of affect in mathematics education. In: McLeod D.B., Adams V.M. (eds) Affect and mathematical problem solving (pp. 245-258). New York, USA: Springer. doi: https://doi.org/10.1007/978-1-4612-3614-6_17
MIDEPLAN. (2017). Costa Rica Índice de Desarrollo Social (IDS) 2017. Recuperado de https://documentos.mideplan.go.cr/share/s/L0GWBZnfRceDJjpxwm7zFQ
OCDE. (2016). Programa para la Evaluación Internacional de los Alumnos. Informe Matemática. Recuperado de https://www.oecd.org/pisa/pisa-2015-results-in-focus-ESP.pdf
Usher, E. L. y Pajares, F. (2009). Sources of self-efficacy in mathematics: A validation study. Contemporary educational psychology, 34(1), 89-101. doi: http://dx.doi.org/10.1016/j.cedpsych.2008.09.002
Zalazar, M. F.; Aparicio, M. M. D.; Ramírez, C. M. y Garrido, S. J. (2011). Estudios preliminares de adaptación de la Escala de Fuentes de Autoeficacia para Matemáticas. Revista Argentina de Ciencias del Comportamiento (RACC), 3(2), 1-6. Recuperado de https://revistas.unc.edu.ar/index.php/racc/article/view/5222
Zamora-Araya, J. A. (2012). Validación de la prueba de diagnóstico en matemática para estudiantes de nuevo ingreso a la Universidad Nacional de Costa Rica, por medio de un modelo de Rasch y de un modelo de ecuaciones estructurales para predecir la nota en el curso de Matemática General (tesis de maestría). Universidad de Costa Rica, San José.
Las actitudes hacia la matemática, el desarrollo social, el nivel educativo de la madre y la autoeficacia como factores asociados al rendimiento académico en la materia (José Andrey Zamora-Araya) en Revista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported licence.
