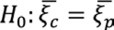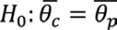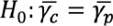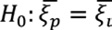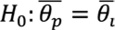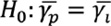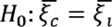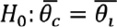| ISSN Electrónico: 2215-3470 DOI: http://dx.doi.org/10.15359/ru.34-1.7 |
UNICIENCIA Vol. 34, N° 1. Enero-Junio, 2020 URL: www.revistas.una.ac.cr/uniciencia Correo electrónico: revistauniciencia@una.cr |
 |
 |
Comparación de parámetros de valor extremo de la distribución generalizada asociada a eventos de precipitación extrema en América Central |
Comparison of parameters of the generalized extreme value distribution associated with extreme rainfall events in Central America
Comparação de parâmetros da distribuição de valores extremos generalizada associada a eventos extremos de precipitação na América Central
|
Helen S. Guillén-Oviedo Departamento Estadística, Universidad del Bío Bío Concepción, Chile. |
Luis R. Cid-Serrano† Departamento Estadística, Universidad del Bío Bío Concepción, Chile. |
Eric J. Alfaro-Martínez Centro de Investigaciones Geofísicas, Escuela de Física Centro de Investigación en Ciencias del Mar y Limnología, Universidad de Costa Rica San Pedro, Costa Rica. |
Received: 1/mar/2019 • Accepted: 23/jul/2019 • Published: 31/jan/2020.
|
Resumen Se utilizó la distribución de valor extremo generalizada (DVEG) para modelar los eventos de lluvia extrema en América Central, durante 30 años, a partir de 1971. Los datos consistieron en registros de precipitaciones diarias en 103 estaciones meteorológicas localizadas en todo el istmo. El área de América Central se dividió en 3 regiones: el Pacífico, el Caribe y la zona intermedia. Con el objetivo de comparar los parámetros de ubicación, escala y forma de la DVEG de esas 3 localidades, se utilizó la prueba de hipótesis Bootstrap. Los resultados del estudio muestran diferencias significativas, especialmente en los parámetros de ubicación y escala entre las 3 regiones. Palabras clave: distribución de valores extremos; lluvia; América Central; vertiente del Pacífico; vertiente del Caribe. Abstract The generalized extreme value distribution (GEVD) was used to model extreme rainfall events in Central America for a period of 30 years, beginning in 1971. Data consisted of daily rainfall records of 103 meteorological stations located throughout the isthmus. Central America was divided into 3 regions: Pacific, Caribbean and an intermediate zone. A bootstrap hypothesis test was used to compare the parameters of location, scale and form of the 3 regions. The results of the study showed significant differences between the 3 regions, mainly in terms of location and scale parameters. Keywords: extreme value distribution; rainfall; Central America; Pacific slope; Caribbean slope. Resumo A distribuição generalizada de valores extremos (DVEG) foi utilizada para modelar os eventos de precipitação máxima na América Central durante 30 anos, a partir de 1971. Os dados consistiram em registros de precipitações diárias em 103 estações meteorológicas localizadas ao longo do istmo. A área da América Central foi dividida em 3 regiões: o Pacífico, o Caribe e a zona intermediária. A fim de comparar os parâmetros de localização, escala e forma da DVEG desses 3 locais, foram utilizados os testes de hipóteses de Bootstrap. Os resultados do estudo mostram diferenças significativas, especialmente nos parâmetros de localização e escala entre as 3 regiões. Palavras-chaves: distribuição de valores extremos; chuva; América Central; vertente do Pacífico; vertente do Caribe. |
Introducción
El Quinto Informe de Evaluación de Cambio Climático (IPCC, 2014) muestra una tendencia creciente en la frecuencia de ocurrencia de eventos extremos en los últimos cincuenta años. Por ejemplo, huracanes más fuertes, heladas más frías, lluvias más profundas, sequías más secas, etc., y es probable que las altas temperaturas, las olas de calor y las fuertes precipitaciones continúen siendo más frecuentes en el futuro. Esto ha provocado un gran interés en estudiar el comportamiento de estos eventos extremos.
La variabilidad de las precipitaciones en América Central es probablemente la variable meteorológica de investigación más relevante en la región (IPCC, 2014). En este marco, este artículo se enfoca en el estudio de las características de distribución de los eventos de lluvias extremas en América Central, establece diferencias entre las vertientes del Caribe y del Pacífico, trabaja con datos diarios de precipitación de los años 1971 a 2000 (30 años) en 103 estaciones ubicadas en toda América Central.
Dado que ambos océanos presentan características oceanográficas y atmosféricas muy diferentes (Amador et al., 2016), las regiones centroamericanas que están más cerca de cada uno de ellos también presentan características climáticas diferentes (Alfaro, 2002), lo que define una gran diversidad de climas que permite el desarrollo de una gran variedad de formas de vida extraordinarias. La región es un área vulnerable al efecto de diferentes fenómenos naturales (Pérez-Briceño et al., 2016).
Los eventos extremos no solo pueden atribuirse al cambio climático, ya que pueden ocurrir naturalmente, sino que se espera que el cambio climático modifique la frecuencia de la ocurrencia de estos eventos, incluidas inundaciones, sequías, tormentas tropicales y olas de calor (IPCC, 2014).
En este sentido, y debido al impacto de las precipitaciones en la economía y la sociedad de los países de América Central, la variabilidad de las precipitaciones es uno de los temas de estudio más importantes en los últimos años (Taylor y Alfaro, 2005). De hecho, el clima ha experimentado un aumento considerable en la frecuencia de los eventos climáticos extremos, lo que hace que su análisis sea relevante en una zona considerada como un “punto caliente” al referirse al cambio climático (IPCC, 2014). También existe una alta probabilidad de que los eventos de lluvia extrema aumenten en frecuencia y magnitud en el futuro, como resultado del calentamiento global (IPCC, 2014).
El clima de América Central está determinado por el mar Caribe y el océano Pacífico (Enfield y Alfaro, 1999). El clima predominante de América Central se puede clasificar como seco-invierno tropical con lluvias muy intensas durante su época lluviosa.
Debido a lo anterior, surge como una línea de investigación, si este comportamiento diferencial se refleja en la frecuencia de la ocurrencia e intensidad de las condiciones extremas, específicamente en los eventos pluviométricos de ambas vertientes; esto, dado que está asociado con procesos y actividades económicas diferenciadas (Amador et al., 2016; Pérez-Briceño et al., 2016). También es necesario determinar si las precipitaciones (extremas) de ambas regiones también pueden modelarse por separado. Para ello, es necesario encontrar modelos estadísticos adecuados que reflejen esas diferencias.
Este estudio se centra en calcular las características distribucionales de los eventos climáticos extremos de precipitación en la Vertiente del Caribe y la Vertiente del Pacífico de América Central.
Marco teórico
Eventos extremos
Estadísticamente, un evento extremo está relacionado con las colas de la distribución de probabilidad de los valores observados, en nuestro caso la cantidad de lluvia, o con las respectivas estadísticas de orden. En este estudio, se consideran extremos los valores que pertenecen al percentil 95 de la distribución, o aquellos detectados como valores atípicos en un diagrama de caja y bigotes.
En general, cuando se habla de eventos extremos se piensa en episodios intensos de corto plazo, como por ejemplo un huracán, lluvias torrenciales o una ola de calor. Sin embargo, más que tratarlos aisladamente, únicamente en términos de duración o intensidad, es de mayor interés estudiarlos desde el punto de vista estadístico; esto es, asociarlos con sus respectivas distribuciones de probabilidad (Izaguirre, 2010).
Para Albeverio et al. (2005), un evento extremo es algo que sucede en un espacio y un tiempo limitado, ya que su aparición puede surgir por azar, por necesidad o por una combinación de ambos; por causas naturales, por el ser humano o ambas y la interpretación de extremo puede ser compleja, pues abarca un conjunto de atributos tales como raro, excepcional, sorprendente y catastrófico, lo que se podría traducir como raro, con baja probabilidad y catastrófico como de gran importancia, esto último respecto del potencial del evento para el impacto y el cambio.
La teoría de los valores extremos ha sido un tema de interés durante mucho tiempo, no solo estadístico sino también ingenieril y científico, y corresponde al área de estadísticas que trata los valores extremos (máximo o mínimo) de una muestra de datos (Izaguirre, 2010, Izaguirre et al. 2010, 2011, 2012, 2013); es decir, los valores ubicados en las colas de la distribución probabilística de la variable en estudio. Generalmente, el concepto de evento extremo está relacionado principalmente con la magnitud del impacto y no con la frecuencia con la que ocurren (Retana, 2012). Sin embargo, Alfaro et al. (2018) y Maldonado et al. (2016, 2013) han usado la frecuencia de eventos extremos para estudiar la predictibilidad en América Central, a lo largo del ciclo anual de las precipitaciones, y han encontrado buena habilidad predictiva de los modelos ajustados. En este contexto, se propone la DGVE como un modelo probabilístico para eventos de lluvia extrema.
Distribución generalizada de valor extremo
Los tres tipos de distribuciones de valor extremo Weibull, Frechet y Gumbel (Wilks, 2011), fueron combinadas en una sola distribución con parametrización común por Von Moises(1954) y Jenkinson(1955) mencionado por Ibañez (2011), la que se conoce como la Distribución generalizada de valor extremo (por sus siglas en inglés, DVEG).
La distribución de probabilidad de la DVEG tiene una función de densidad de probabilidad (fdp) de la forma:
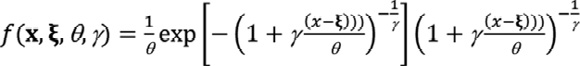, (1)
Donde, 𝜉, θ, and 𝛶 representan los parámetros de ubicación, escala y forma de la distribución, con 𝛶 ≠ 0. Note que θ y 1 +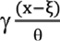 
deben ser mayores que cero y que los parámetros de forma y ubicación pueden tomar cualquier valor real.
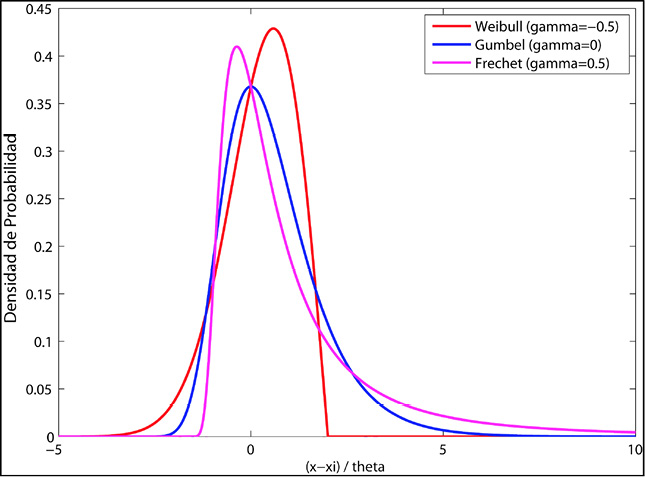
Para 𝛶 > 0, 𝛶 < 0 y 𝛶 = 0 se obtienen las distribuciones de Frechet, Weibull y Gumbel respectivamente. La distribución Frechet tiene una cola pesada, ya que va disminuyendo lentamente, como en el caso de la distribución de Cauchy, la de Pareto y una variedad de distribuciones mixtas. En la distribución de Weibull la cola está acotada, también es el caso de la distribución uniforme y la Beta. La distribución Gumbel tiene una cola delgada (ligera), al igual que la distribución normal, exponencial, gamma y logarítmica. La Gráfica 1 presenta la función de densidad de la DVEG para cada una de las 3 clases de distribuciones basadas en el parámetro de forma.
La DVEG se recomendó para el análisis de eventos como la frecuencia de inundaciones en el Reino Unido y se usó para modelar los fenómenos naturales extremos como los flujos de los ríos, el nivel del mar, las precipitaciones y la contaminación del aire, y para estudiar la distribución máxima de precipitación diaria o anual (Kotz y Nadarajah, 2000 y Johnson et al., 1994).
Gráfica 1
Ejemplos de la función de densidad de probabilidad de la distribución Frechet, Gumbel y Weibull.
Nota: Fuente propia del estudio.
Sin embargo, los datos meteorológicos en general no deberían generar ninguna preocupación mientras permanezcan dentro de una banda relativamente estrecha alrededor de la media y no contengan eventos climáticos ubicados más allá de dicha banda de confianza (Berlaint et al., 2004). La situación cambia, por ejemplo, cuando se registran observaciones que superan un umbral. Los datos de lluvia y viento proporcionan ilustraciones con un impacto en la sociedad, y son uno de los temas más comunes para el debate, con las preguntas sobre el calentamiento global y el cambio climático. En general, resulta de interés analizar las observaciones y registros máximos y mínimos en el tiempo, ya que podrían generar consecuencias negativas. Las concentraciones de ozono por hora en el este de los Estados Unidos es uno de los ejemplos de aplicaciones mencionadas por Le y Zidek (2006). El análisis se refiere a concentraciones de ozono por hora de más de 120 días durante el verano de 1997, más específicamente, los 16 sitios con la fracción más baja de valores perdidos por hora (menos de 18 en las 2,880 horas).
Hann y Ferreira (2006) citan tres casos en los que se utiliza la teoría del valor extremo. Una de ellas es la construcción de diques para prevenir inundaciones en lugares que se encuentran bajo el nivel del mar, para determinar la altura correcta de estos (Castillo et al., 2004; Izaguirre et al. 2010; 2012; 2013). También mencionan que dentro del campo de la ingeniería oceánica, es bien sabido que la altura de la ola es el factor principal a tener en cuenta para el diseño, plataformas marinas, rompeolas, diques y otras obras portuarias, y se basan en el conocimiento de la distribución de probabilidad de las olas más altas. Para Castillo et al. (2004) las condiciones climáticas extremas afectan el desarrollo de la vida animal y humana, y la agricultura. Proponen que, en lugar de centrarse en los valores medios (de temperatura, precipitación, etc.), la principal preocupación sea la evaluación de la probabilidad de ocurrencia de eventos extremos, para lo cual se cuenta con un modelo de probabilidad adecuado, como el proporcionado por la DVEG.
El objetivo de esta investigación es estudiar las características de distribución de los eventos de precipitaciones extremas en América Central y establecer si existen diferencias estadísticamente significativas para los parámetros de la DVEG entre las vertientes del Caribe y del Pacífico.
Metodología
Datos
Los datos corresponden a series de tiempo de precipitaciones diarias desde el año 1971 hasta el año 2000 e incluyen los registros de 103 estaciones meteorológicas ubicadas en toda América Central (Figura 1 y Gráfica 2). Los datos fueron proporcionados por los servicios meteorológicos e hidrológicos de la región. La Gráfica 2 muestra la ubicación de las estaciones meteorológicas, que exhiben una buena cobertura espacial.
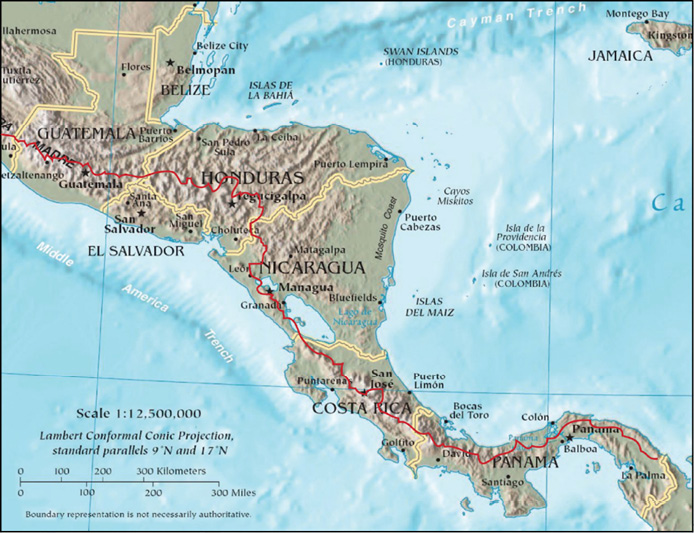
Figura 1.
Mapa de América Central. La línea roja separa las vertientes del Pacífico y el Caribe, Imbach P., L. Molina, B. Locatelli, O. Roupsard, G. Mahe, R. Neilson, L. Corrales, (2012). Extraido de: Modeling Potential Equilibrium States of Vegetation and Terrestrial Water Cycle of Mesoamerica under Climate Change Scenarios. J. of Hydrometeorology, 665-680.
Cada serie contiene los registros de precipitación de 30 años, correspondiente a 10957 observaciones diarias a partir de enero de 1971. Los eventos de lluvia extrema se definieron como aquellos ubicados en el percentil 95 de la distribución de la lluvia, de modo que cada estación contenía 547 valores de lluvia extrema correspondientes al 5 % superior de la precipitación observada en cada estación (Gráfica 2). Lo anterior, con el fin de obtener independencia en las observaciones (Coles, 2001).
Gráfica 2
Distribución geográfica de las 103 estaciones meteorológicas.
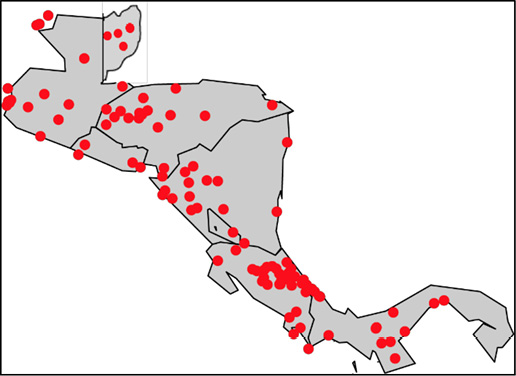
Nota: Fuente propia del estudio.
A continuación, las estaciones se clasificaron según su ubicación en una de las dos vertientes, Pacífico y Caribe y en la línea divisoria. La Gráfica 3 muestra la clasificación de las 103 estaciones, con 43 estaciones claramente ubicadas en la vertiente del Caribe (en rojo); 25 en la vertiente del Pacífico (en azul) y 35 de ellas ubicadas muy cerca de la línea divisoria que divide las vertientes del Caribe y del Pacífico (en verde). Inicialmente para establecer si existen diferencias entre los parámetros de la DVEG de las vertientes del Caribe y el Pacífico de América Central, las estaciones se agruparon de acuerdo con su ubicación geográfica en cada una de las dos vertientes. Sin embargo, en la clasificación surge una zona intermedia, las cuales pueden presentar influencia de ambos sistemas meteorológicos.
Gráfica 3
Ubicación geográfica de las estaciones meteorológicas. En rojo los correspondientes a la vertiente del Caribe; en azul los de la vertiente del Pacífico y en verde los de la zona intermedia.
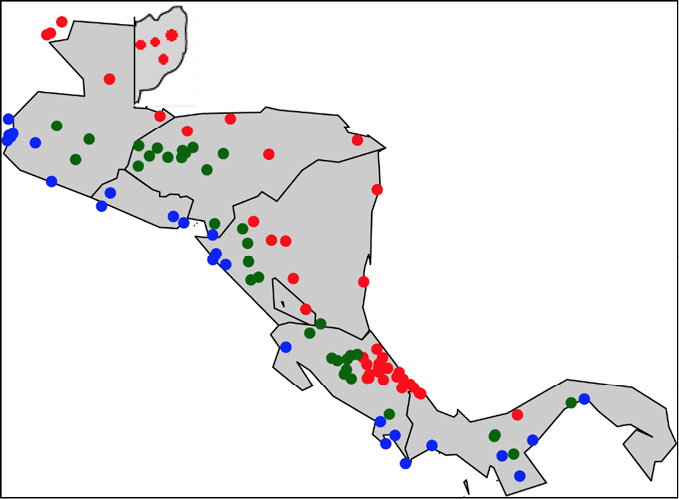
Nota: Fuente propia del estudio.
Para caracterizar la DVEG en cada una de las 103 estaciones, se obtuvieron los estimadores de máxima verosimilitud de los parámetros de ubicación (ξ), escala (θ) y forma (γ). Como no hay expresiones analíticas para los estimadores de los parámetros, se utilizaron métodos de optimización numéricos, como el método de Nelder-Mead, implementado en el proyecto R, estos están predefinidos y entregan las estimaciones máximas posibles de los parámetros de la distribución en cada uno de los tres grupos.
Análisis discriminante
Para validar la clasificación inicial de las estaciones meteorológicas realizadas solo en función de su ubicación geográfica, se utilizó el análisis discriminante lineal (ADL) (Hair et al., 1999). El ADL se usa comúnmente para predecir la pertenencia a un grupo o categoría según los valores observados de varias variables continuas que caracterizan a los sujetos que se clasificarán, en nuestro caso, las estaciones meteorológicas. Específicamente, el análisis discriminante predice una variable de clasificación (Y) (nominal u ordinal) basada en respuestas continuas conocidas (X). Los datos para un análisis discriminante consisten en una muestra de observaciones con pertenencia a un grupo conocido (anterior) junto con sus valores en las variables continuas. En nuestro estudio, la clasificación geográfica en las tres regiones se usó como clasificación previa y las variables de clasificación corresponden a los valores estimados de los tres parámetros de la DVEG en cada estación.
Para realizar el análisis se deben verificar varios supuestos como lo son el supuesto de normalidad de las variables independientes y la igualdad entre las matrices de covarianzas de los grupos.
En este estudio se realizó el análisis discriminante con el SPSS, donde se verificó el supuesto de normalidad de las variables independientes por medio de la prueba de Kolmogorov Smirnov para una muestra y la igualdad entre las matrices de covarianzas de los grupos, para esto se usó la prueba M de Box. Es importante mencionar que la prueba de igualdad de matrices de covarianzas, puede verse afectada por el tamaño de muestra, cuando esta es muy grande.
Pruebas de hipótesis para la comparación de los parámetros de ubicación, forma y escala
Para cumplir con el objetivo de establecer, si existen diferencias en los parámetros de la DVEG como modelo probabilístico, en el estudio de eventos de precipitación extrema entre la vertiente del Caribe y vertiente del Pacífico en América Central, debemos contrastar las siguientes hipótesis
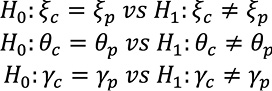
Donde 𝜉c, 𝜃c, 𝛶c y 𝜉p, 𝜃p, 𝛶p corresponden a los parámetros de ubicación 𝜉, escala 𝜃 y forma 𝛶 de las vertientes Caribe y Pacífico respectivamente.
Se compararon los promedios de las estimaciones de cada uno de los parámetros en las respectivas vertientes, mediante las pruebas de hipótesis correspondientes. El uso de los promedios permitió realizar una comparación global, considerando que no se dispone de un criterio válido que sirva para definir un patrón de comparaciones uno a uno, de los parámetros para cada estación. Por lo que las pruebas de hipótesis son:
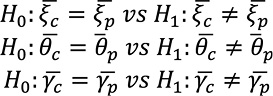
Debido a que las estimaciones de los parámetros considerados no tienen distribución conocida, se debe utilizar una prueba de hipótesis tal que su estadístico de prueba no requiera conocer la distribución de los datos; para ello se utilizó el método Bootstrap (Efron & Tibshirani,1993), por medio del paquete computacional R. Es importante aclarar que estas pruebas se realizaron para cada parámetro y se compararon dos a dos los promedios de las estimaciones de los parámetros para Caribe vs Pacífico.
Resultados
Estaciones Caribe y Pacífico y análisis discriminante
Dado que las estaciones ubicadas en la zona intermedia pueden afectar la comparación de los parámetros de la DVEG para la vertiente Caribe y vertiente Pacífico, se realiza el análisis de discriminante.
Se verificó el supuesto de normalidad de las variables independientes y se obtuvo que las variables siguen una distribución normal. Se verificó la igualdad entre las matrices de covarianzas de los grupos, y se obtuvo que se rechaza la igualdad entre las matrices de covarianzas; pero esto puede estar afectado por el tamaño de la muestra, ya que, si la muestra es grande, esta prueba pierde efectividad.
Se realizó el análisis para las 103 estaciones clasificadas entre vertiente Caribe y vertiente Pacífico de donde se obtuvo un porcentaje de clasificación correcta del 58,3 %; además, se obtuvo un 55,9 % de clasificación correcta para las estaciones del Caribe y un 62,9 % para las estaciones de Pacífico (Ver tabla 1). Estos porcentajes de clasificación corresponden a 60 estaciones clasificadas correctamente.
Tabla 1
Resultados de la clasificación por medio del análisis discriminante para las 103 estaciones
|
Clasificación geográfica |
Grupo pertenencia pronosticado |
Total |
|||
|
Caribe |
Pacífico |
||||
|
Original |
Recuento |
Caribe Pacífico |
38 13 |
30 22 |
68 35 |
|
Porcentaje |
Caribe Pacífico |
55,9 37,1 |
44,1 62,9 |
100 100 |
|
Nota: Fuente propia del estudio.
Dado que hay un importante número de estaciones que están ubicadas muy cerca de la línea divisoria geográfica de las vertientes (Ver Gráfica 2), la probabilidad de clasificar correctamente en una de las vertientes disminuye; para las estaciones más alejadas de la zona intermedia la probabilidad de correcta clasificación aumenta, por lo que realizamos un análisis discriminante para las 68 estaciones que están claramente clasificadas en la vertiente Caribe y vertiente Pacífico; esto es, sin considerar aquellas estaciones ubicadas en la zona intermedia, pero antes verificamos el supuesto de normalidad. Se concluyó que las variables siguen una distribución normal y se verificó la igualdad entre las matrices de covarianzas, la cual rechaza la igualdad entre las matrices de covarianzas, lo que, como se mencionó, está asociado al tamaño de la muestra.
Los resultados del análisis discriminante para las estaciones que están claramente clasificadas en la vertiente Caribe y vertiente Pacífico, arrojó que un 72,1 % de clasificación correcta, correspondiente a un 69,8 % de correcta clasificación para las estaciones de la vertiente Caribe y un 76 % para las estaciones de la vertiente Pacífico. Estos porcentajes de clasificación corresponden a 49 estaciones clasificadas correctamente.
Comparando la Tabla 1 con la Tabla 2, observamos que hubo un aumento del porcentaje de clasificación correcta para las estaciones del Caribe de un 10,9 % y de un 13,1 % para las estaciones del Pacífico. Ello verifica que las estaciones de la zona intermedia no pueden ser clasificadas correctamente, como pertenecientes a una de las vertientes, pues tienen influencia de los sistemas meteorológicos del Pacífico y del Caribe.
Tabla 2
Resultados de la clasificación por medio del análisis discriminante para las 68 estaciones
|
Clasificación geográfica |
Grupo pertenencia pronosticado |
Total |
|||
|
Caribe |
Pacífico |
||||
|
Original |
Recuento |
Caribe Pacífico |
30 6 |
13 19 |
43 25 |
|
Porcentaje |
Caribe Pacífico |
69,8 24,0 |
30,2 76.0 |
100 100 |
|
Nota: Fuente propia del estudio.
La Tabla 3 muestra el análisis discriminante para las 3 clasificaciones Caribe, Pacífico y zona intermedia, del cual obtuvimos un porcentaje de clasificación correcta de 56,3 %, lo que corresponde a un 65,1 % para la vertiente Caribe, un 32 % para la vertiente Pacífico y un 62,9 % para las estaciones en la zona intermedia. El supuesto de normalidad se verificó al igual que el supuesto de igualdad de las matrices de covarianzas que resultó también significativo como en los casos anteriores.
Tabla 3
Análisis discriminante para las 103 estaciones, porcentaje de clasificación correcta (56.3 %)
|
Clasificación geográfica |
Grupo pertenencia pronosticado |
Total |
||||
|
Caribe |
Pacífico |
Zona intermedia |
||||
|
Original |
Recuento |
Caribe Pacífico Zona intermedia |
28 7 6 |
11 8 7 |
4 10 22 |
43 25 35 |
|
Porcentaje |
Caribe Pacífico Zona intermedia |
65,1 28 17,1 |
25,6 32 20 |
9,3 40 62,9 |
100 100 100 |
|
Nota: Fuente propia del estudio.
A partir de esto se concluye que las estaciones ubicadas en la zona intermedia introducen un factor de incertidumbre en la clasificación, por lo que se decidió incorporarlas como un tercer grupo de comparación.
Estimación de los parámetros de la DVEG
La tabla 4 muestra los valores medios estimados de los parámetros para cada vertiente. Estos parámetros están relacionados con la cantidad de lluvia extrema, la dispersión (varianza), y la orientación de la asimetría de la distribución (izquierda o derecha), respectivamente
Tabla 4
Tamaño de muestra (n) y valores medios de las estimaciones para cada parámetro en cada una de las tres regiones
|
Zona- parámetro |
N |
Ubicación |
Escala |
Forma |
|
Pacífico |
43 |
34,94 |
8,904 |
0,560 |
|
Caribe |
25 |
38,91 |
10,760 |
0,598 |
|
Intermedia |
35 |
28,46 |
7,680 |
0,530 |
Nota: Fuente propia del estudio.
La Gráfica 4 muestra la distribución espacial de las estaciones meteorológicas (en rojo las correspondientes a la vertiente del Caribe; en azul las de la vertiente del Pacífico y en verde las de la zona intermedia) El diámetro de los puntos es proporcional a los valores estimados del parámetro de ubicación. La Gráfica 4 muestra valores más altos en la zona costera, mientras que los valores más pequeños se ubican hacia los valles interiores. Esto indica que en esas regiones la cantidad de lluvia es mayor que la registrada en la vertiente del Pacífico. También se encontraron valores más altos en el norte y el sur de la costa del Pacífico. En la zona intermedia, las estimaciones no siguen un patrón específico.
Gráfica 4
Distribución espacial de las estimaciones del parámetro de ubicación para las 103 estaciones. El diámetro del punto es proporcional a los valores de las estimaciones del parámetro de escala en cada una de las estaciones. En rojo las estimaciones de la vertiente del Caribe, en azul las estimaciones de la vertiente del Pacífico y en las estimaciones verdes de la zona intermedia
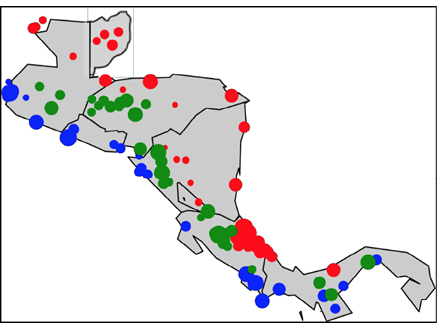
Nota: Fuente propia del estudio.
La Gráfica 5 muestra la distribución espacial de las estimaciones del parámetro de escala. El diámetro de los puntos es proporcional a los valores estimados. Aquí, pocos valores más altos de las estimaciones se ubican en el norte y sur de ambas vertientes. Además, los valores más altos también se encuentran cerca de la costa y los más pequeños hacia los valles interiores. Los valores más altos de los parámetros pueden interpretarse como que representan una mayor variabilidad de la cantidad de lluvia, debido a los eventos de lluvia extrema, de modo que los círculos más pequeños en la parte central del continente pueden interpretarse como que en esas áreas la cantidad de lluvia extrema es más estable que en la costa.
Gráfica 5
Distribución espacial de las estimaciones del parámetro de escala para las 103 estaciones, el diámetro del punto es proporcional a los valores de las estimaciones del parámetro de escala en cada una de las estaciones. En rojo las estimaciones de la vertiente del Caribe, en azul las estimaciones de la vertiente del Pacífico y en las estimaciones verdes de la zona intermedia
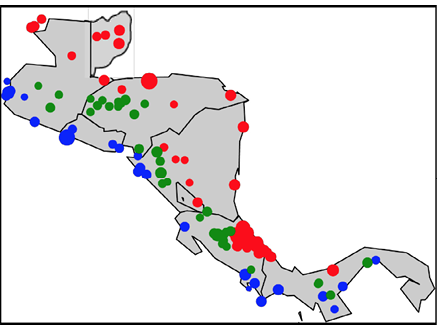
Nota: Fuente propia del estudio.
La Gráfica 6 muestra la distribución espacial de las estimaciones del parámetro de forma para la DVEG de las vertientes del Caribe, del Pacífico y de la zona intermedia. Se puede apreciar que las estimaciones no siguen un patrón predeterminado; es decir, los valores se distribuyen independientemente de su ubicación geográfica. Sin embargo, la mayoría de los valores más pequeños de las estimaciones se ubican en la zona intermedia y en el sur de la vertiente del Pacífico, correspondientes a Costa Rica y Panamá.
Gráfica 6
Distribución espacial de las estimaciones de parámetros de forma para las 103 estaciones, el diámetro del punto es proporcional a los valores de las estimaciones de parámetros de escala en cada estación. En rojo, las estimaciones para las estaciones ubicadas en la vertiente del Caribe, en azul las de la vertiente del Pacífico y en verde las ubicadas en la zona intermedia
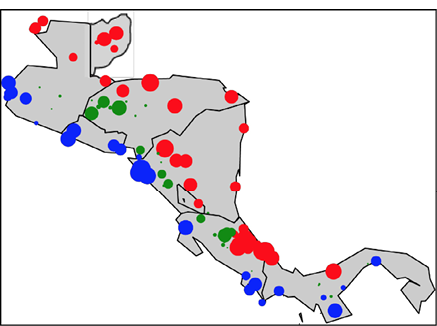
Nota: Fuente propia del estudio.
Como conclusiones del comportamiento de las funciones de densidad de la DVEG al variar sus parámetros y la relación con las lluvias extremas, se tiene que el parámetro de ubicación 𝜉, se relaciona con la cantidad de lluvia extrema, el parámetro de escala 𝜃, está relacionado con la dispersión (varianza) de los eventos de lluvia extrema y el parámetro de forma 𝛶, representa el nivel de apuntamiento (en un punto específico del dominio de la variable aleatoria).
Hipótesis para la comparación de los parámetros de ubicación, forma y escala
Para comparar los parámetros de la DVEG entre la vertiente del Caribe, vertiente del Pacífico y la zona intermedia, probamos la hipótesis de que los valores medios de los parámetros (ubicación, forma y escala) para cada vertiente son iguales. Se hicieron tres pruebas distintas, una para cada parámetro. El uso del promedio de los parámetros estimados para cada área nos permitió realizar una comparación global, pues se considera que no existe un criterio válido que sirva para definir un patrón de comparaciones uno a uno de los parámetros para cada temporada, las estimaciones de los parámetros no tienen distribución conocida, utilizamos el método Bootstrap para contrastar las hipótesis. Se concluyó que había diferencias significativas cuando el valor de p ≤ 0,05, es decir, se utilizó un nivel de significancia del 5 %.
El promedio de los parámetros se comparó por separado para cada par de vertientes, con los resultados mostrados en las tablas a continuación, es decir, Pacífico vs. Caribe (Tabla 5); Pacífico vs zona intermedia (Tabla 6); y zona intermedia vs. Caribe (Tabla 7).
La Tabla 5 muestra los resultados de las pruebas de hipótesis cuando se comparan los valores medios de los parámetros de ubicación de las estaciones que están claramente en la vertiente del Caribe frente a la vertiente del Pacífico. Se obtuvo que el promedio de los parámetros de ubicación (𝜉) no difieren significativamente entre las dos regiones (valor p = 0,1998), este resultado se interpreta como que la cantidad de lluvia asociada a eventos extremos en las laderas del Caribe y del Pacífico no difiere significativamente. El resultado para la comparación del promedio de los parámetros de escala (𝜃) indica que el parámetro es significativamente más alto en el Caribe (valor p = 0,0259), con el parámetro de forma (𝛶) solo ligeramente superior (valor p = 0,0684). Estos resultados indican que existe una mayor variabilidad (en la cantidad de lluvia extrema) en la vertiente del Caribe.
Tabla 5
Resumen de pruebas de hipótesis para la comparación de parámetros de la DVEG del total de las estaciones que están claramente en el Caribe y en el Pacífico
|
Hipótesis/Zona |
Caribe |
Pacífico |
Valor-p |
|
|
38,91 |
34,94 |
0,1998 |
|
|
10,78 |
8,90 |
0,0259 |
|
|
0,60 |
0,56 |
0,0684 |
Nota: Fuente propia del estudio.
Además de las pruebas de hipótesis ya mencionadas, realizamos pruebas para comparar los parámetros de la DVEG, pero en este caso considerando como un grupo a las estaciones ubicadas en la zona intermedia. Así que se comparan la vertiente Caribe y la vertiente Pacífico con la zona intermedia.
La Tabla 6, muestra el resumen de las pruebas de hipótesis para la comparación de los valores medios de los parámetros de la DVEG entre la vertiente Pacífico y la zona intermedia, donde se observa que los valores-p de la hipótesis del parámetro de ubicación es significativa, por lo que se rechaza la hipótesis nula. Este resultado indica que el parámetro de ubicación presenta diferencias significativas en la parametrización de la DVEG entre las vertientes Pacífico y la zona intermedia. Mientras que para el parámetro de escala y forma no se puede rechazar la hipótesis nula. Esto se interpreta como que la cantidad de lluvia (asociada con eventos de lluvia extrema) en la vertiente del Pacífico es mayor que en la zona intermedia. Además que no existe diferencias en la variabilidad de la magnitud de las lluvias extremas y en la mayor frecuencia de cantidad de agua caída, de lluvias extremas entre la vertientes Pacífico y la zona intermedia.
Tabla 6
Resultados de pruebas de hipótesis para la comparación de parámetros de la DVEG de las estaciones que están claramente en el Pacifico y las que están en la zona intermedia
|
Hipótesis/Zona |
Pacífico |
Intermedia |
Valor-p |
|
|
34,94 |
28,46 |
0,0368 |
|
|
8,90 |
7,68 |
0,0649 |
|
|
0,56 |
0,53 |
0,1036 |
Nota: Fuente propia del estudio.
La Tabla 7 muestra los resultados de las pruebas de hipótesis al comparar los valores medios de los parámetros de la vertiente del Caribe frente a la zona intermedia. Podemos concluir entonces que los tres parámetros presentan diferencias significativas en la parametrización de la DVEG entre la vertiente del Caribe y la zona intermedia.
Tabla 7
Resultados de pruebas de hipótesis para la comparación de parámetros de la DVEG de las estaciones que están claramente en el Caribe y las que están en la zona intermedia
|
Hipótesis/Zona |
Caribe |
Intermedia |
Valor-p |
|
|
38,91 |
28,46 |
0,0366 |
|
|
10,78 |
7,68 |
0,0001 |
|
|
0,60 |
0,53 |
0,0183 |
Nota: Fuente propia del estudio.
Como el parámetro de ubicación está asociado con la cantidad de lluvia extrema, este resultado indica que la cantidad de lluvia asociada con eventos extremos en la vertiente del Caribe es mayor que la cantidad de lluvia asociada con eventos extremos en la zona intermedia. Dado que la diferencia en el parámetro de escala es altamente significativa y el parámetro de escala está asociado con la dispersión de la variable, concluimos que en el Caribe los eventos de lluvia extrema tienen una variabilidad (dispersión) mucho mayor que en la zona intermedia. Y, por último, la mayor frecuencia de cantidad de agua caída, de lluvias extremas en la vertiente del Caribe es mayor que en la zona intermedia.
Discusión y conclusiones
El estudio mostró que hay un comportamiento diferente de episodios de lluvias extremas en las regiones del Pacífico y el Caribe cuando se caracterizan a través de su DVEG correspondiente y sus parámetros respectivos. La comparación del promedio de los parámetros para cada región mostró diferencias significativas entre las vertientes del Pacífico y el Caribe en América Central cuando se estiman por separado para cada vertiente y también respetan una zona intermedia.
Las Gráficas 4, 5 y 6 muestran que los parámetros son mucho más pequeños en la parte central del continente. Esto puede interpretarse como que en las áreas centrales del continente existe una menor variabilidad de los eventos extremos, es menos severa y con una variabilidad más pequeña que en las regiones costeras. Esta conclusión coincide con el significado de la prueba de hipótesis utilizada al comparar zona intermedia vs las laderas del Pacífico y del Caribe. Según Maldonado et al. (2018), eso podría explicarse porque la topografía es el principal modulador local de la variabilidad en la región. Fernández et al. (1996) exploraron la variabilidad de las precipitaciones con la altitud en América Central al examinar la distribución vertical de las lluvias en Costa Rica a lo largo de un perfil topográfico que atravesó el país desde las costas del Pacífico hasta las del Caribe. El perfil de montaña, con un pico más alto de aproximadamente 3000 m, está orientado perpendicular a los vientos alisios del noreste a gran escala prevalecientes. Su análisis de las cantidades de lluvia y las variaciones estacionales y diurnas en 14 estaciones pluviométricas ubicadas en o cerca del perfil topográfico, revela una variación considerable con la altitud. Las precipitaciones máximas en los lados de barlovento (Caribe) y de sotavento (Pacífico) de la cordillera principal se producen en altitudes intermedias en lugar de en las cimas de las montañas (ver también Chacón & Fernández, 1985). El promedio anual máximo de 7735 mm en el lado de barlovento y 6692 mm en el lado de sotavento se observaron a aproximadamente 2000 m y 800 m respectivamente.
La interacción entre los terrenos con el flujo inducido proveniente de la ZCIT del Pacífico, debido a algunos sistemas sinópticos que prevalecen, produce un tipo de perturbación que contribuye a la precipitación en América Central, que se denomina “temporales” (Hastenrath, 1991; Fernández et al., 1996). Estos son períodos de lluvias débiles moderadas, casi continuas, que duran varios días y afectan a una región relativamente grande. Su definición incluye la condición de que el viento debe ser débil; sin embargo, Amador et al. (2003) han demostrado que en algunos casos los vientos pueden ser intensos y duraderos.
Fernández et al. (1996) identifican al menos cuatro configuraciones sinópticas que pueden eventualmente generar condiciones para un temporal, como una vaguada profunda de la troposfera media y baja, una vaguada de los vientos oestes en la troposfera alta, los empujes de aire frío de América del Norte (Zárate-Hernández, 2013; 2014), y el efecto directo e indirecto de los huracanes (Peña y Douglas, 2002). Por otro lado, Velásquez (2000) también encontró que los sistemas de nubes de bajo nivel que viajan hacia el oeste (Peña y Douglas, 2002) sobre el Caribe y el Pacífico, que no están necesariamente asociados con las intrusiones de aire frío en latitudes medias. La frecuencia de estos eventos presenta una gran variabilidad interanual e intraestacional, y su relación con el ENOS o con otras señales climáticas a gran escala aún no está clara (Amador et al., 2006).
Como se menciona en Maldonado et al. (2018), las circulaciones de brisa marina son otros moduladores regionales relevantes del clima, en islas y penínsulas, ya que favorecen el desarrollo de sistemas convectivos. Estas circulaciones están marcadas por un ciclo diurno debido al contraste térmico entre el litoral y el mar que puede estar asociado a un ciclo diurno de precipitación. Sin embargo, en regiones costeras con topografía compleja cercana, como América Central, el flujo inducido puede afectar la distribución temporal y espacial de las características de mesoescala en la precipitación. Además de eso, existe evidencia en regiones con características similares al istmo centroamericano (es decir, la costa oeste de Colombia), donde la brisa marina puede penetrar en las montañas cercanas a la costa de un valle hasta aproximadamente 100 km (Mapes et al., 2003)
Otro control del clima por la topografía en América Central se incluyó en el trabajo de Amador et al. (2006). Explicaron que los cambios en la intensidad de los vientos alisios en el mar Caribe y el golfo de México ejercen un control importante sobre las precipitaciones a través de las interacciones viento-topografía. Los frentes fríos de invierno boreal que descienden de las latitudes extra-tropicales generan fuertes chorros de viento de bajo nivel a lo largo de los pasajes de Tehuantepec, Papagayo y el Golfo de Panamá. Alfaro y Cortés (2012) y Alfaro et al. (2012) estudiaron este aspecto en Bahía Culebra, Golfo de Papagayo, en la costa norte del Pacífico de Costa Rica, que es un área de surgencias estacionales.
Agradecimientos
EA agradece a los siguientes proyectos inscritos en la Vicerrectoría de Investigación, Universidad de Costa Rica: 805-B8-766 (Redes), B9-454 (Grupos), B7-286 (UCREA), B7-507 (apoyado por CONICIT y MICITT). Los autores agradecen a los Servicios Meteorológicos e Hidrológicos de la región por suministrar los datos usados en esta investigación
Referencias
Albeverio, S.; Jentsch, V. & Kantz, H. (2005). Extreme Events in Nature and Society. Alemania: Springer.
Alfaro, E. (2002). Some Characteristics of the Annual Precipitation Cycle in Central America and their Relationships with its Surrounding Tropical Oceans. Tópicos Meteorológicos y Oceanográficos, 9(2), 88-103.
Alfaro, E. J., & Cortés, J. (2012). Atmospheric forcing of cool subsurface water events in Bahía Culebra, Gulf of Papagayo, Costa Rica. Revista de Biología Tropical, 60, 173–186. doi: http://dx.doi.org/10.15517/rbt.v60i2.20001
Alfaro, E. J., Chourio, X., Muñoz, Á. G., & Mason, S. J. (2018). Improved seasonal prediction skill of rainfall for the Primera season in Central America. Int. J. Climatol, 38: e255-e268. doi: http://dx.doi.org/10.1002/joc.5366
Alfaro, E. J., Cortés, J., Alvarado, J. J., Jiménez, C., León, L., Sánchez-Noguera, C., & Ruiz, E. (2012). Clima y temperatura sub-superficial del mar en Bahía Culebra, Golfo de Papagayo, Costa Rica. Revista de Biologia Tropical, 60(2), 159–171. doi: https://doi.org/10.15517/rbt.v60i2.20000
Amador, J. A., Alfaro, E. J., Lizano, O. G., & Magaña, V. O. (2006). Atmospheric forcing of the eastern tropical Pacific: A review. Progress in Oceanography, 69(2–4), 101–142. doi: https://doi.org/10.1016/j.pocean.2006.03.007
Amador, J. A., Chacón, J. R., & Laporte, S. (2003). Climate and climate variability in the Arenal Basin of Costa Rica. In H. Díaz & B. Morehouse (Eds.) (pp. 317–349). Kluwer: Academic Publishers. doi: https://doi.org/10.1007/978-94-015-1250-3_14
Amador, J. A., Rivera, E. R., Durán-Quesada, A. M., Mora, G., Sáenz, F., Calderón, B., & Mora, N. (2016). The easternmost tropical Pacific. Part I: A climate review. Revista de Biología Tropical, 64 (1), S1-22. doi: https://doi.org/10.15517/rbt.v64i1.23407
Beirlant, J., Goegebeur, Y. & Teugels, J. (2004). Statistics of Extremes Theory and Applications. John Wiley & Sons Ltd. doi: http://dx.doi.org/10.1002/0470012382
Castillo, E., Hadi, A., Balakrishnan, N., & Sarabia, J. (2004). Extreme Value and Related Models with Applications in Engineering and Science. USA: Wiley-Interscience.
Chacón, R. E., & Fernandez, W. (1985). Temporal and spatial rainfall variability in the mountainous region of the Reventazón river basin, Costa Rica. Journal of Climatology, 5(2), 175–188. doi: https://doi.org/10.1002/joc.3370050205
Coles, S. (2001). An Introduction to Statistical Modeling of Extreme Values. Gran Britain: Springer.
Efron, B., & R. Tibshirani, R. (1993). Introduction to the Bootstrap. New York, Chapman & Hall.
Enfield D., & Alfaro, E. (1999). The Dependence of Caribbean Rainfall on the Interaction of the Tropical Atlantic and Pacific Oceans. J. of Climate (12), 1093-2103. doi: https://doi.org/10.1175/1520-0442(1999)012<2093:TDOCRO>2.0.CO;2
Fernández, W., Chacón, R., & Melgarejo, J. (1996). On the rainfall distribution with altitude over Costa Rica. Revista Geofísica, 44, 57–72. doi: http://hdl.handle.net/10669/668
Hair, J., Anderson, R., Tatham, R., & Black, W. (1999). Análisis multivariante. Madrid: Prentice Hall Iberia.
Hann, L., & Ferreira, A. (2006). Extreme Value Theory: An Introduction. USA: Springer.
Hastenrath, S. (1991). Climate Dynamics of the Tropics. Dordrecht: Springer Netherlands.
Ibañez, A. (2011). Análisis estadístico de valores extremos y aplicaciones. (Tesis inédita de doctorado). Universidad de Granada, Granada, España.
Imbach P., Molina, L., Locatelli, B., Roupsard, O., Mahe, G., Neilson, R., Corrales, L., Scholze, M., & Ciais, P. (2012). Modeling Potential Equilibrium States of Vegetation and Terrestrial Water Cycle of Mesoamerica under Climate Change Scenarios. J. of Hydrometeorology, 13, 665-680. doi: https://doi.org/10.1175/JHM-D-11-023.1
IPCC. (2014). Climatic Climate Change 2014. Synthesis Report Summary for Policymakers.
Izaguirre, C. (2010). Estudio de la variabilidad climática de valores extremos de oleaje. (Unpublished doctoral dissertation), University of Cantabria, Spain.
Izaguirre, C., Méndez, F., Espejo, A., Losada, I. & Reguero, B. (2013). Extreme wave climate changes in Central-South America. Springer Science+Business Media Dordrecht, (119), 277-290. doi: https://doi.org/10.1007/s10584-013-0712-9
Izaguirre, C., Méndez, F., Menéndez, M., & Losada, I. (2011). Global extreme wave height variability based on satellite data. Geophysical Research Letters, 38, 1-6. doi: https://doi.org/10.1029/2011GL047302
Izaguirre, C., Méndez, F., Menéndez, M., Luceño, A., & Losada, I. (2010). Extreme wave climate variability in southern Europe using satellite data. Journal of Geophysical Research, (115), 1-13. doi: https://doi.org/10.1029/2009JC005802
Izaguirre, C., Menéndez, M., Camus, P., Méndez, F., Mínguez, R., & Losada, I. (2012). Exploring the interannual variability of extreme wave climate in the Northeast Atlantic Ocean. Ocean Modelling, 59-60, 31-40. doi: https://doi.org/10.1016/j.ocemod.2012.09.007
Johnson N., Kotz, S., & Balakrishnan, N. (1994). Continuous Univariate Distributions. New York: Wiley-Interscience.
Kotz, S., & Nadarajah, S. (2000). Extreme Value Distributions: theory and applications. London: Imperial College Press.
Le, N., & Zidek, J. (2006). Statistical Analysis of Environmental Space-Time Processes. USA: Springer.
Maldonado, T., Alfaro, E. J., & Hidalgo, H. G. (2018). A review of the main drivers and variability of Central America’s Climate and seasonal forecast systems. Revista de Biología Tropical, 66(Suppl.1), S153-S175. doi: http://dx.doi.org/10.15517/RBT.V66I1.33294
Maldonado, T., Alfaro, E., Fallas, B., & Alvarado, L. (2013). Seasonal prediction of extreme precipitation events and frequency of rainy days over Costa Rica, Central America, using Canonical Correlation Analysis. Advances in Geosciences, 33, 41-52. doi: https://doi.org/10.5194/adgeo-33-41-2013
Maldonado, T., Rutgersson, A., Alfaro, E., Amador, J., & Claremar, B. (2016). Interannual variability of the midsummer drought in Central America and the connection with sea surface temperatures. Advances in Geosciences, 42, 35-50, doi: http://dx.doi.org/10.5194/adgeo-42-35-2016
Mapes, B. E., Warner, T. T., Xu, M., Negri, A. J., Mapes, B. E., & Xu, M. (2003). Diurnal Patterns of Rainfall in Northwestern South America. Part II: Model Simulations. Monthly Weather Review, 131(5), 799–812. doi: https://doi.org/10.1175/1520-0493(2003)131<0830:DPORIN>2.0.CO;2
Peña, M., & Douglas, M. W. (2002). Characteristics of Wet and Dry Spells over the Pacific Side of Central America during the Rainy Season. Monthly Weather Review, 130(12), 3054–3073. doi: https://doi.org/10.1175/1520-0493(2002)130<3054:COWADS>2.0.CO;2
Pérez-Briceño, P.M., Alfaro, E., Hidalgo, H. & Jiménez, F. (2016). Distribución espacial de impactos de eventos hidrometeorológicos en América Central. Revista de Climatología, 16, 63-75.
Retana, J. (2012). Eventos hidrometeorológicos extremos lluviosos en Costa Rica desde la perspectiva de la adaptación al cambio en el clima. Tópicos meteorológicos y oceanográficos, 1, 52 -64. doi: http://dx.doi.org/10.15359/rca.44-2.1
Taylor, M. & Alfaro, E. (2005). Climate of Central America and the Caribbean, Climate of. In Encyclopedia of World Climatology (Oliver JE, Ed.), Springer, Netherlands, pp. 183-189. doi: https://doi.org/10.1007/1-4020-3266-8_37
Velásquez, R. (2000). Mecanismos físicos de variabilidad climática y eventos extremos en Venezuela. Universidad de Costa Rica.
Wilks, D. (2011). Statistical Methods in the Atmospheric Sciences (Vol. 100, 3ra ed.) California: Academic Press.
Zárate-Hernández, E. (2013). Climatología de masas invernales de aire frío que alcanzan Centroamérica y el Caribe y su relación con algunos índices árticos. Top. Meteor. Oceanogr., 12(1), 35 – 55.
Zárate-Hernández, E. (2014). Influencia de las masas invernales de aire frío sobre el chorro de bajo nivel del Caribe y sus ramas. Top. Meteor. Oceanogr., 13(2), 19–40.
