Revista UNICIENCIA
Uniciencia Vol. 38(1), January-December, 2024
E-ISSN: 2215-3470
DOI: https://dx.doi.org/10.15359/ru.38-1.2
Guía de valoración de la idoneidad didáctica de procesos de estudio de la diferencial
Didactic Suitability Assessment Guide of Educational Processes for the Differential
Guia para avaliação da adequação didática de processos de estudo da diferencial
Manuel Alejandro Verón1*, Belén Giacomone2, Luis Roberto Pino-Fan3
Received: Sep/26/2022 • Accepted: Mar/17/2023 • Published: Jan/1/2024
|
Resumen [Objetivo] En este artículo se describe el proceso de elaboración de una Guía de valoración de la idoneidad didáctica de un proceso de estudio del concepto de diferencial de una función. El objetivo que se persigue es proponer un instrumento que promueva, oriente y apoye el análisis y la reflexión del profesorado en torno a los procesos de enseñanza y aprendizaje del concepto de diferencial. [Metodología] El método de investigación empleado es el análisis de contenido y toma como punto de partida la revisión sistemática de los conocimientos didáctico-matemáticos en investigaciones claves. El análisis está orientado por las dimensiones o facetas que intervienen en un proceso educativo: epistémica, cognitiva, afectiva, instruccional y ecológica cuyos componentes y criterios se fundamentan en noción de idoneidad didáctica propuesta por el enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS). [Resultados] La construcción de la Guía de valoración de la idoneidad didáctica introduce una metodología para la reconstrucción del significado de referencia para el estudio de la diferencial en sus diversas facetas. Además, esta guía representa una herramienta potente para el profesor en el momento del diseño, implementación y valoración de procesos de estudio teniendo en cuenta los diversos significados de la diferencial, sus conexiones, sus potenciales conflictos semióticos y sus relaciones con otros conceptos. [Conclusiones] En línea con el marco teórico de referencia, se concluye que su uso idóneo permitiría al profesor tomar decisiones didácticas argumentadas sobre la propia gestión del proceso didáctico teniendo en cuenta el contexto educativo. Palabras clave: Diferencial; conocimientos didáctico-matemáticos; idoneidad didáctica; práctica reflexiva. Abstract [Objective] This article describes the process of preparing a Guide for the Assessment of Didactic Suitability of a process for studying the concept of the differential of a function. The objective of this exercise was to propose an instrument to promote, guide and support teachers’ analysis of, and reflection on, teaching and learning processes of the differential concept. [Methodology] The research method used was content analysis, and its starting point was a systematic review of didactic-mathematical knowledge in key research. The analysis was guided by the dimensions or facets that characterize an educational process – epistemic, cognitive, affective, instructional and ecological – whose components and criteria are based on the notion of didactic suitability proposed in the Onto-semiotic Approach to Mathematical Knowledge and Instruction (OSA). [Results] The construction of the Didactic Suitability Assessment Guide introduced a methodology for the reconstruction of the reference meaning for the study of various facets of the differential. In addition, this guide represents a powerful tool for teachers at the time of designing, implementing. and evaluating study processes, taking into account the various meanings of the differential, its connections, its potential semiotic conflicts and its relationships with other concepts. [Conclusions] In line with the theoretical reference framework, it is concluded that its ideal use would allow teachers to make informed decisions about management of the didactic process, taking into account its educational context. Keywords: Didactic-mathematical knowledge; didactic suitability; reflective practice. Resumo [Objetivo] Este artigo descreve o processo de elaboração de um guia para avaliar a adequação didática de um processo a fim de estudar o conceito de diferencial de uma função. O objetivo buscado é propor um instrumento que promova, oriente e apoie a análise e a reflexão dos professores sobre os processos de ensino e aprendizagem do conceito de diferencial. [Metodologia] O método de pesquisa utilizado é a análise de conteúdo e tem como ponto de partida a revisão sistemática do conhecimento didático-matemático em pesquisas-chave. A análise está norteada pelas dimensões ou facetas que intervêm em um processo educacional: epistêmica, cognitiva, afetiva, instrucional e ecológica cujos componentes e critérios se baseiam na noção de adequação didática proposta pela abordagem ontosemiótica do conhecimento e da instrução matemática (EOS). [Resultados] A construção do Guia de avaliação da adequação didática introduz uma metodologia para a reconstrução do significado de referência para o estudo da diferencial em suas várias facetas. Além disso, esse guia representa uma ferramenta poderosa para o professor ao projetar, implementar e avaliar processos de estudo, levando em conta os diferentes significados da diferencial, suas conexões, seus possíveis conflitos semióticos e suas relações com outros conceitos. [Conclusões] De acordo com o marco teórico de referência, conclui-se que seu uso ideal permitiria que o professor tomasse decisões didáticas fundamentadas sobre a própria gestão do processo didático, considerando o contexto educacional. Palavras-chave: diferencial; conhecimento didático-matemático; adequação didática; prática reflexiva. |
La diferencial es uno de los conceptos fundamentales en el estudio del cálculo, tanto en el bachillerato como en diversas carreras universitarias. Docentes y futuros docentes deben afrontar complejos desafíos para abordar los problemas didácticos asociados a este concepto e intentar responder a las demandas que reclama la comunidad científica. Sin bien existe una gran cantidad de investigaciones sobre las dificultades que presentan los estudiantes al abordar este concepto (Gómez, 2019; López-Gay y Martínez Torregrosa, 2005), no son tantas las que abordan cuáles son los conocimientos didáctico-matemáticos que debería tener en cuenta el profesor para su enseñanza (Castro y Pino-Fan, 2021).
Las dificultades documentadas en la bibliografía se relacionan con las dimensiones epistémica, cognitiva, ecológica e instruccional del proceso de estudio de la diferencial. Desde la dimensión epistémica, autores como Artigue, Menigoux y Viennot (1990), Bos (1974), Kleiner (2012), López-Gay (2001), Pulido (1997), Tall (1981), Taylor (1974), Valdivé y Garbin (2008) y Verón y Giacomone (2021) estudiaron la evolución histórica y epistemológica de la diferencial y sus conexiones con nociones tales como cantidad infinitamente pequeña, infinitesimal, variación infinitesimal, aproximación lineal, aproximación o estimación lineal del incremento, entre otros. Desde la dimensión cognitiva, estudios como los de Gómez (2019), Martínez-Torregrosa, López-Gay, Gras-Martí, Torregrosa-Gironés (2002) y López-Gay, Sáez, Torregrosa (2015) plantean que una de las dificultades para la comprensión de la diferencial está presente en la diversidad de significados, producto de su evolución histórica.
Por otro lado, los diversos contextos de uso y los sentidos que van construyendo los estudiantes a partir de las situaciones-problemas aplicadas a distintas áreas, como las matemáticas, física, ingeniería o ciencias experimentales, hace que surjan nuevos conflictos cognitivos. Así, la diversidad de objetos (definiciones, términos, expresiones) imbricados en cada contexto hace que no quede claro qué es la diferencial y para qué se utiliza (Ely, 2021). Uno de los principales usos de la diferencial se encuentra en la modelización, ya que permite realizar un estudio de los fenómenos de cambio en diferentes disciplinas; destaca, de esta manera, la importancia de un aspecto de la dimensión ecológica. Pero como consecuencia de este uso interdisciplinario se producen disparidades de significados, como lo evidencian los estudios de Dray y Monogue (2010) y Hu y Rebello (2013).
En relación con la dimensión instruccional, las investigaciones mencionadas señalan dificultades desencadenadas por la forma en que se presenta el estudio de la diferencial en los libros de texto; estas se generan, principalmente, debido al uso excesivo de diferentes definiciones sin explicar los cambios considerados (Gómez, 2019; Oldenburg, 2016; Pulido, 1997).
Considerando que la mejora y optimización de los procesos de enseñanza y de aprendizaje deberían ser competencia del profesor de matemáticas, en el marco del enfoque ontosemiótico se ha desarrollado la noción de idoneidad didáctica (Godino, 2013) como una herramienta metodológica que propone un sistema de indicadores globales para apoyar el diseño de tareas significativas, su implementación y la valoración justificada de todo el proceso de estudio. Este sistema de valoración global debe ser ajustado para cada contenido matemático que se quiera abordar mediante el estudio de los conocimientos didáctico-matemáticos necesarios para su enseñanza efectiva. Por ejemplo, Araya, Pino-Fan, Medrano y Castro (2021) proponen criterios para diseñar tareas de la noción límite; Beltrán-Pellicer, Godino, Giacomone (2018) desarrollan indicadores específicos para el estudio de la probabilidad; Pino-Fan y Parra-Urrea (2021) elaboran criterios para el estudio de las funciones; Ruz, Molina-Portillo y García (2019) plantean una guía para valorar procesos de instrucción en didáctica de la estadística.
Teniendo en cuenta los resultados de las investigaciones en torno al estudio de la diferencial, en este artículo abordamos la siguiente pregunta de investigación:
¿Qué aspectos y criterios debería tener en cuenta un profesor para optimizar los procesos de enseñanza y aprendizaje del concepto de diferencial?
Para responder esta pregunta, en esta investigación se presenta la elaboración de una Guía de valoración de la idoneidad didáctica de un proceso de estudio de la diferencial, la cual se prevé como un referente para los profesores al momento de planificar y reflexionar sobre sus clases y tomar decisiones fundamentadas.
A continuación, se presenta el marco teórico y el problema específico de investigación. Luego, se describe la metodología empleada seguida de los resultados obtenidos. Finalmente, se presentan algunas conclusiones y líneas de investigación.
Marco teórico y problema específico de investigación
Desde la perspectiva del enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS) (Godino, Batanero y Font, 2007; 2020), se consideran seis dimensiones o facetas que determinan los focos de atención del análisis didáctico: epistémica, cognitiva, afectiva, interaccional, mediacional y ecológica. Para clasificar un proceso de instrucción como adecuado, en este marco se desarrolló la noción idoneidad didáctica que aporta componentes y criterios generales para valorar cada una de dichas facetas (Figura 1).

Figura 1. Facetas y componentes del proceso instruccional que pueden ser focos de la investigación.
Extraído de Godino, Batanero, Burgos y Gea (2021, p. 10).
Cada faceta se puede valorar con criterios generales referidos a cada componente que se define como una “norma de corrección que establece cómo debería realizarse un proceso de enseñanza y aprendizaje” (Breda, Font y Pino-Fan, 2018, p. 264).
La noción de idoneidad didáctica se considera como un criterio sistémico de optimización de un proceso de enseñanza de las matemáticas y se define en estos términos:
El grado en que dicho proceso (o una parte del mismo) reúne ciertas características que permiten calificarlo como óptimo o adecuado para conseguir la adaptación entre los significados personales logrados por los estudiantes (aprendizaje) y los significados institucionales pretendidos o implementados (enseñanza), teniendo en cuenta las circunstancias y recursos disponibles (entorno). (Godino et al., 2020, p. 11)
Así, la idoneidad didáctica supone la articulación coherente de las seis facetas relacionadas con las correspondientes del proceso instruccional (Godino et al., 2007):
• Idoneidad epistémica: grado de representatividad de los significados institucionales implementados (o pretendidos), respecto de un significado de referencia.
• Idoneidad ecológica: grado en que el proceso de estudio se ajusta al proyecto educativo del centro, la escuela y la sociedad y a los condicionamientos del entorno en que se desarrolla.
• Idoneidad cognitiva: grado en que los significados pretendidos/ implementados estén en la zona de desarrollo potencial de los estudiantes, así como la proximidad de los significados personales logrados a los significados pretendidos/implementados.
• Idoneidad afectiva: grado de implicación (interés, motivación, …) del alumnado en el proceso de estudio. Está relacionada tanto con factores que dependen de la institución como con factores que dependen básicamente del estudiante y de su historia escolar previa.
• Idoneidad interaccional: un proceso de enseñanza-aprendizaje tendrá mayor idoneidad desde el punto de vista interaccional, si las configuraciones y trayectorias didácticas permiten, por una parte, identificar conflictos semióticos potenciales y, por otra parte, resolver los conflictos que se producen durante el proceso de instrucción.
• Idoneidad mediacional: grado de disponibilidad y adecuación de los recursos materiales y temporales necesarios para el desarrollo del proceso de enseñanza aprendizaje. (p. 133)
Por medio de la elaboración de la Guía de valoración de la idoneidad didáctica (GVID) se pretende introducir una estrategia metodológica para la reconstrucción de un significado de referencia para el estudio de la diferencial, en las diversas facetas (Beltrán-Pellicer et al., 2018). Como resultado, la GVID se presenta como una herramienta para la reflexión sistemática y detallada de los procesos de enseñanza y aprendizaje en sus fases de diseño, implementación y evaluación (Beltrán-Pellicer et al., 2018).
La metodología se basa en el análisis de contenido (Cohen, Manion y Morrison, 2007) que permite establecer, procesar y revisar dimensiones o categorías cualitativas, describir tendencias, características del contenido y realizar inferencias válidas a partir de los datos.
Las unidades de análisis se determinan a partir de las facetas, componentes, subcomponentes y criterios de la idoneidad didáctica para el análisis de contenido de las investigaciones referidas a la enseñanza y aprendizaje del diferencial. Así, se logra la construcción de la GVID para el estudio de la diferencial, cuyo proceso introduce una metodología para realizar la reconstrucción del significado de referencia para el estudio de un concepto en sus diversas facetas (Beltrán-Pellicer et al., 2018).
Criterios de idoneidad didáctica de procesos de estudio de la diferencial
En Godino, Batanero, Rivas y Arteaga (2013) se plantea:
La faceta epistémica se refiere al contenido matemático que se estudia, entendido desde una perspectiva institucional, y apoyado en una epistemología matemática centrada en las situaciones-problemas, en las prácticas realizadas para su resolución, así como en las configuraciones de objetos y procesos matemáticos que intervienen y emergen en las tales prácticas. (pp. 52-53)
Es importante tener en cuenta que la diferencial es un concepto polisémico (López-Gay et al., 2015) porque tiene varios significados, funciones y usos diferentes en matemáticas, física, ingeniería y en las ciencias experimentales (Arcos, 2004; Oldenburg, 2016; Verón, 2020).
Significados
Diversos autores han elaborado modelos parciales o clasificaciones de los significados de diferencial según los usos y aplicaciones que hacen los estudiantes con el objetivo de comprender y afrontar las distintas dificultades educativas asociadas (Dray y Manogue, 2010; Ely, 2021; Hu y Rebello, 2013; López-Gay et al., 2015; Oldenburg, 2016; Pulido, 2010; Valdivé y Garbin, 2008; Von Korff y Rebello, 2014). En esta misma línea, Verón y Giacomone (2021) realizaron una descripción detallada de los significados parciales de diferencial a partir de un estudio histórico epistemológico donde abordan la complejidad ontosemiótica del concepto (Font, Pino-Fan y Breda, 2020).
En Verón y Giacomone (2021) se presentan cuatro significados parciales de diferencial asociado a Leibniz, Cauchy, Fréchet y Robinson, los cuales se describen brevemente a continuación.
Las situaciones-problemas de las que emerge de manera clave la diferencial de Leibniz están relacionadas con las cantidades infinitamente pequeñas usadas en el cálculo de la tangente a una curva (Araya et al., 2021; Pino-Fan, Godino y Font, 2011), la longitud de la curva, el área de una región o el volumen de un sólido de revolución (Edwards, 1979). La diferencial como un incremento infinitesimal fue de gran ayuda para resolver muchos problemas de física (Badillo, Font y Azcárate, 2005).
Las situaciones-problemas que relacionan la diferencial con las cantidades como variables o incrementos arbitrarios, las cuales son infinitesimales cuando su límite tiende a cero, se asocian a la diferencial de Cauchy; por ejemplo, en el cálculo de la inclinación de la curva (Verón y Giacomone, 2021), en problemas de geometría, física y economía que involucran el trabajo con límites (Araya et al., 2021), en situaciones que involucran la derivada como cociente de diferenciales en el cálculo de puntos máximos, mínimos e inflexión (Pino-Fan et al., 2011), en el contexto de la integral (Burgos, Bueno, Pérez y Godino, 2021).
Cuando se requiere realizar una aproximación local de la curva, una estimación lineal o tangencial, para describir el comportamiento de un determinado fenómeno físico, químico, biológico o geométrico, se utilizan aproximaciones y funciones lineales, que caracterizan al diferencial de Fréchet (p.e. López-Gay et al., 2018). En estas situaciones-problemas no se requiere que la diferencial sea infinitamente pequeña, sino que ∆𝑓 – d𝑓 sea infinitamente pequeño respecto de ∆x (Martínez-Torregrosa, López-Gay y Gras-Martí, 2006).
La diferencial de Robinson se caracteriza por considerar a los infinitesimales como números hiperreales en el campo del análisis no estándar (Kleiner, 2012), como lo plantean Keisler (2000) para el cálculo de la pendiente a una función. También, para problemas de velocidad, tasa de cambios y funciones de acumulación considerando al diferencial como un incremento infinitesimal de x, en el marco del análisis no estándar (Ely, 2021).
El lenguaje algebraico y simbólico es una de las principales características de la diferencial de Leibniz, por su persistencia en el tiempo con el surgimiento de las expresiones como ∆x, ∆y, dx, dy, x + dx, y + dy, (dx)2 (Edwards, 1979; Kleiner, 2012; Martínez-Torregrosa et al., 2002; Pulido, 1997). El lenguaje natural y geométrico se caracteriza por considerar los conceptos como cantidades geométricas variables, es decir, considerar las variables como cantidades o magnitud (Bos, 1974; Pulido, 1997). En la diferencial de Cauchy, interviene el lenguaje simbólico, algebraico y funcional con el empleo de los símbolos como 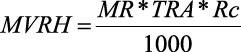 y las relaciones funcionales entre la diferencial y la derivada, en expresiones como
y las relaciones funcionales entre la diferencial y la derivada, en expresiones como  (Verón, 2020).
(Verón, 2020).
Con la diferencial de Frechét se emplea un lenguaje natural y geométrico, al trabajar con la aproximación lineal como la recta tangente a la curva; y algebraico, simbólico y funcional cuando se utilizan expresiones como 𝑓: A ⟶ R, ∆x, d𝑓, d𝑓 = 𝑓´ (a) dx, d𝑓(a, dx) = 𝑓´(a)dx y ≈ para indicar que ∆𝑓 ≈ d𝑓. Las expresiones y símbolos mencionados anteriormente están presente en la diferencial de Robinson.
Los conceptos y definiciones que caracterizan la diferencial de Leibniz son “cantidades infinitamente pequeñas, diferencia, polígono infinitoangular, triángulo diferencial, tangente, subtangente, semejanza, ecuación proporcional” (Verón, 2020, p. 41), definiendo el diferencial como:
La diferencia de dos valores sucesivos de x es la diferencial dx, y similarmente para dy. Se supone que las cantidades dx y dy no son cero sino incomparablemente pequeñas, y por lo tanto despreciables, con respecto a los valores de las variables x e y. (Edwards, 1979, p. 261)
Al incorporar los conceptos de inclinación, cuerda, curva, variable, tangente trigonométrica, límite, convergencia, razón de incrementos, cociente de diferenciales y función derivada (Verón, 2020), se corresponde con la diferencial de Cauchy: “la diferencial de la variable independiente x no es otra cosa que la constante finita ℎ. Por tanto, la ecuación d𝑓(x) = h𝑓´(x) viene a ser d𝑓(x) = 𝑓´(x).dx o lo que viene a ser lo mismo, dy = y´dx” (Cauchy, 1823, p. 13). Para Cauchy (1821), “una cantidad variable se vuelve infinitamente pequeña, cuando su valor numérico disminuye indefinidamente para converger hacia el límite cero” (p. 26).
En la diferencial de Frechét se agregan los conceptos de aplicación lineal y homogénea, función, aproximación, estimación lineal, error, entre otros (Verón, 2020). De esta manera, la diferencial se define como la estimación lineal del incremento respecto al cambio de variable. Se entiende que la diferencial es una función que puede tomar cualquier valor y su expresión diferencial va a estar sujeta a la condición de que (∆𝑓 – d𝑓) sea infinitamente pequeña respecto a ∆x (López-Gay, 2001). Esto quiere decir que d𝑓 no es infinitamente pequeño, sino que la diferencia entre el incremento y la diferencial es infinitamente pequeña respecto a ∆x (López-Gay, 2001). Además, es necesario destacar que la función diferencial d𝑓 es una función de dos variables (Martínez-Torregrosa et al., 2002) ya que depende del punto x = a y del diferencial de x, cuya notación es: d𝑓(a, dx) = 𝑓´(a) dx
En el contexto de la diferencial de Robinson entran en juego los conceptos de infinitésimo, número hiperreal, número real y números infinitamente próximos (Robinson, 1966). La diferencial de x se define como una variable independiente dx = ∆x y la diferencial de y es la variable dependiente dy dada por dy = 𝑓´(x)dx (Keisler, 2000). En relación con los conceptos de curva, pendiente y razón de incrementos infinitesimales, la relación entre la derivada y el cociente de diferenciales es la igualdad: 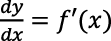 ; mientras que la derivada y el cociente incremental difieren en un infinitésimo:
; mientras que la derivada y el cociente incremental difieren en un infinitésimo:  (Verón, 2020).
(Verón, 2020).
Las principales proposiciones y propiedades que caracterizan la diferencial de Leibniz son: “un incremento infinitesimal dx en x, produce un incremento infinitesimal dy en y ” (Martínez-Torregrosa et al., 2002). En el marco de la diferencial de Cauchy se considera que una cantidad infinitamente pequeña es “una variable cuyo valor numérico disminuye indefinidamente” (Cauchy, 1821, p. 27).
Las proposiciones que intervienen en la diferencial de Frechét son: “∆𝑓 = 𝑓´(a) dx + ɛdx”, “el incremento de la función se puede escribir como una suma de una aplicación lineal y homogénea del incremento de x y una función ɛ que tiende a cero cuando ∆x tiende a cero” (Verón y Giacomone, 2021, p. 17), y “∆𝑓 ≈ 𝑓´(a)dx”, “∆𝑓 ≈ d𝑓”.
En la diferencial de Robinson, al plantear la razón de incrementos infinitesimales, por ejemplo  , surgen varias proposiciones, por ejemplo, “el número hiperreal 2x0 + ∆x no es un número real, sino que está infinitamente próximo al número real 2x0” (Verón, 2020, p. 40).
, surgen varias proposiciones, por ejemplo, “el número hiperreal 2x0 + ∆x no es un número real, sino que está infinitamente próximo al número real 2x0” (Verón, 2020, p. 40).
En cuanto a los procedimientos, se destaca en el marco de Leibniz el de “diferencia de la ecuación” que consiste en “incrementar las variables x e y en una cantidad infinitamente pequeña dx y dy, respectivamente” (Verón, 2020, p. 42), por ejemplo, para y = x2 es y + dy = (x + dx)2. Además, Leibniz plantea que para encontrar la tangente a una curva hay que “dibujar una línea recta que une dos puntos de la curva que tienen una distancia infinitamente pequeña, es decir, el lado prolongado del polígono infinito angular que para nosotros es lo mismo que la curva” (Bos, 1974, p. 19). En cambio, en el marco de Cauchy, los procedimientos de cálculos se realizan con el proceso de paso al límite dando lugar a la derivada de la función en el punto (x, y) (Verón, 2020).
En el marco de la diferencial de Frechét se destaca el procedimiento donde se plantea el incremento de la función f como ∆𝑓 = 𝑓´(a)dx + ɛdx y que ɛ tiende a cero cuando ∆x tiende a cero, entonces el ∆𝑓 ≈ 𝑓´(a)dx. Los procedimientos que se encuentran en el marco del análisis no estándar consisten en plantear la razón de incrementos infinitesimales y resolver mediante el cálculo algebraico con números hiperreales (Verón, 2020).
Los argumentos que se utilizan, en el marco del cálculo de Leibniz, surgen de la siguiente consideración:
La curva [se considera] como un polígono de infinitos lados, lo que permite determinar el triángulo diferencial y la semejanza con el triángulo formado por la subtangente, la ordenada y la tangente. A partir de establecer la semejanza entre los triángulos, se establecen las ecuaciones proporcionales que permiten hallar el valor de la subtangente y encontrar la tangente. (Verón y Giacomone, 2021, p. 11)
En el marco del cálculo de Cauchy, los argumentos son: “la definición de inclinación de la curva, la tangente trigonométrica como la razón de los incrementos, el límite y la consideración de las cantidades infinitamente pequeñas” (Verón, 2020, p. 32).
En la diferencial de Frechét, la validación se debe a la utilización de la definición de función, límite, incremento de la función ∆𝑓 = d𝑓 + ɛ∆ donde ε tiende a cero cuando Δ tiende a cero y la diferencial como una aplicación lineal y homogénea del incremento de x (Verón, 2020). En cambio, en el marco del diferencial de Robinson, se utiliza la definición de números hiperreales y de las propiedades algebraicas de las operaciones con números hiperreales (Verón, 2020).
Los significados parciales de la diferencial no son exclusivos de un nivel educativo o carrera específica, su estudio, por lo general, se encuentra en los cursos avanzados del bachillerato y en primeros cursos de cálculo de las carreras universitarias. Con frecuencia, en los libros de textos de cálculo, el abordaje de la diferencial es meramente instrumental y su uso se reduce a aplicaciones de una fórmula o al cálculo de errores, cuyas prácticas operativas están relacionadas con el significado de la diferencial de Cauchy. A partir del análisis de los resultados de las investigaciones y de los significados de la diferencial, se considera necesario incluir en los procesos instruccionales situaciones-problemas que impliquen el abordaje de la diferencial de Leibniz, cuyos objetos matemáticos están asociados a las ideas más intuitivas de infinitesimales que dieron origen al concepto. Sin embargo, para el estudio del diferencial de Frechét resulta necesario tener disponible una serie de conocimientos previos, los cuales implican que el estudiante ha realizado un recorrido previo para favorecer la comprensión de los objetos implicados en este significado parcial. Por lo tanto, es recomendable que su abordaje se realice posterior al tratamiento de los anteriores. En cambio, la diferencial de Robinson, que surge en el marco del análisis no estándar, dependerá del enfoque elegido por los cursos de cálculo, si se parten de los infinitesimales o del estudio de los límites.
A partir de los conocimientos didáctico-matemáticos estudiados, determinamos, en la Tabla 1, los indicadores de idoneidad epistémica en relación con los objetos primarios de los significados de la diferencial. En la Tabla 2, avanzamos sobre la identificación de las relaciones, procesos y potenciales conflictos epistémicos que intervienen y emergen en el estudio de la diferencial. Las tablas son el resultado de la adaptación de los criterios generales planteados en Godino (2013) y Godino, Batanero, Burgos y Gea (2021).
Indicadores específicos de los objetos primarios de la idoneidad epistémica para el estudio de la diferencial
|
Componentes |
Indicadores |
|
Significados |
Situaciones-problemas |
|
-Se plantea una muestra representativa de situaciones-problemas que muestren y relacionen los diversos significados de la diferencial involucrando las cantidades infinitesimales, variables cuyos límites son infinitésimos y aproximaciones o estimaciones lineales. -Se proponen situaciones de contextualización, ejercitación, aplicación y de generación de problemas en matemáticas y en las ciencias experimentales (problematización) para el estudio de cambios infinitesimales por los propios estudiantes. -Se plantean situaciones que propician la utilización de la diferencial para la modelización y representación de las variaciones, cambios o acumulación de diversos fenómenos de matemáticas, física, ingeniería y de las ciencias experimentales. |
|
|
Lenguajes |
|
|
-Se emplean diferentes registros y representaciones para describir la diferencial (natural, algebraico, simbólico, gráfico, funcional, etc.), indicando sus conexiones. -Se utiliza un nivel de lenguaje adecuado a los estudiantes que se dirige. -Se emplean términos idóneos para describir la diferencial en distintos contextos, como cantidades pequeñas, cantidades infinitamente pequeñas, incremento infinitesimal, tangente, inclinación, aproximación lineal, pendiente, derivada, etc. -Se proponen situaciones de expresión matemática e interpretación, en los diferentes registros mencionados. Por ejemplo : |
|
|
Conceptos |
|
|
-Se realiza una presentación clara de los conceptos fundamentales de la diferencial y se adaptan al nivel educativo al que se dirigen. -Se presentan las definiciones del dx, dy, incremento de la función, derivada, cantidad infinitesimal, variación infinitesimal, razón de diferencial, incremento infinitesimal, pendiente, estimación lineal tangencial, aproximación, error, etc. -Se proponen situaciones donde los estudiantes tengan que generar o negociar definiciones que intervienen y emergen en el estudio de la diferencial. |
|
|
Proposiciones |
|
|
-Se presentan las proposiciones fundamentales de la diferencial en forma clara y se adaptan al nivel educativo al que se dirigen. Por ejemplo: “un incremento infinitesimal dx en x, produce un incremento infinitesimal dy en y” (Martínez-Torregrosa et al., 2002). -Se proponen situaciones donde los estudiantes tengan que generar o negociar proposiciones sobre las interpretaciones y sentidos que atribuye a la diferencial, según el contexto de uso. |
|
|
Procedimientos |
|
|
-Se presentan los procedimientos fundamentales de la diferencial en forma clara y se adaptan al nivel educativo al que se dirigen. Por ejemplo: “diferencia de la ecuación” que consiste en incrementar las variables x e y en una cantidad infinitamente pequeña dx y dy, respectivamente (Leibniz), el proceso de paso al límite para plantear la derivada como el cociente de diferenciales (Cauchy) o el incremento de la función se puede escribir como una suma de una aplicación lineal y homogénea del incremento de x y una función ɛ que tiende a cero cuando ∆x tiende a cero) (Fréchet) (Verón, 2020). |
|
|
Argumentos |
|
|
-Las proposiciones y procedimientos se explican y argumentan (se justifican y demuestran) de forma adecuadas según el nivel educativo a que se dirigen. -Se usan representaciones geométricas para apoyar y reforzar las argumentaciones. -Se promueven situaciones donde el estudiante tenga que argumentar. |
Nota: Fuente propia de la investigación.
Se considera relevante establecer relaciones entre los significados parciales del diferencial y, en consecuencia, entre las prácticas, objetos y procesos que emergen en la resolución de las situaciones-problemas teniendo en cuenta el grado de generalidad y formalización de los objetos intervinientes (Verón y Giacomone, 2021). Ejemplo de estos son las relaciones entre su representación simbólica (dx, dy, d𝑓) y algunos conceptos como la derivada, integral y ecuaciones diferenciales (Ely, 2021; Gómez, 2019), tasa de cambio (Frank y Thompson, 2021).
Además, autores como Harel (2021), Martínez-Planell y Trigueros (2021), Thompson y Harel (2021) destacan la importancia del estudio de la linealización o aproximación lineal, cuyas prácticas están asociadas al significado parcial de la diferencial, para establecer relaciones entre el cálculo de funciones reales y el cálculo multivariable.
En la diferencial de Leibniz, se destacan los procesos de conceptualización de la diferencial como cantidades de longitud infinitamente pequeñas y la representación del triángulo diferencial y los correspondientes elementos diferenciales dx, dy y ds (Verón, 2020). El proceso de algoritmización surge al establecer la ecuación proporcional que relaciona las cantidades de magnitud geométrica, en este caso longitudes de segmentos (Verón, 2020). Al momento de matematizar cambios pequeños o infinitamente pequeños de diversos fenómenos de estudio provenientes de las matemáticas, la física, química, biología, economía y las ingenierías interviene el proceso de modelización (López-Gay et al., 2015).
Con la diferencial de Cauchy, se destaca el proceso de conceptualización del diferencial como una variable que tiene límite cero, como lo refleja Kitcher (1984, p. 247) al mencionar que “cuando los valores absolutos sucesivos de una variable disminuyen indefinidamente de tal manera que sea menor que cualquier cantidad dada, esa variable se convierte en lo que se llama infinitesimal. Dicha variable tiene cero para su límite”. Además, se puede resaltar el proceso de modelización e identificación de los infinitesimales en el procedimiento de cálculo donde la inclinación de la cuerda tiende a la inclinación de la curva, cuando los puntos que definen a la cuerda se aproximan infinitamente y la distancia que los separa es una variable que tiene por límite cero (Verón, 2020).
Con la diferencial de Frechét, se destaca la conceptualización de la diferencial como una aplicación lineal y homogénea que no necesariamente es infinitamente pequeño, sino que su expresión está sujeta a que ∆𝑓 – d𝑓 sea infinitamente pequeño respecto de ∆x. Otro proceso importante es el de modelización, ya que el comportamiento de la función en un punto es aproximadamente igual al de la diferencial de la función considerándola como mejor aproximación local de la curva (Alibert y Legrand, 1989).
En el marco de la diferencial de Robinson se destaca el proceso de conceptualización de la diferencial, como un número hiperreal (infinitesimal), y el proceso de algoritmización en el cálculo de pendiente al establecer relaciones entre la derivada, cociente de diferenciales, cociente de incrementos infinitesimales y que el número hiperreal 2x0 + ∆x está infinitamente próximo al número real 2x0 (Keisler, 2000).
Dada su complejidad y los diferentes significados con los cuales se presenta, varias investigaciones plantean la necesidad de realizar un estudio histórico epistemológico del concepto de diferencial; resaltan el problema epistemológico que representa (Artigue, 1995; Cordero-Orosio, 1991; García Jiménez, 2018; Gómez, 2019; Hu y Rebello, 2013; Pulido, 1997).
Las dificultades que presentan los estudiantes son del tipo estructural, relacionadas con el cálculo algebraico, pero también conceptual, relacionadas con la comprensión del objeto (Orton, 1983). Por otro lado, se plantea que las dificultades cognitivas están estrechamente relacionadas con el significado que se pretende enseñar (Gómez, 2019), lo que predispone de manera directa los conceptos que definen la diferencial.
López-Gay et al. (2015) y Martínez Uribe, Pluvinage y Montaño Zetina (2017) señalan conflictos en el uso y la representación del diferencial en las diferentes asignaturas que abordan el tema, principalmente entre cálculo y física.
Además, Artigue et al. (1990), López-Gay (2001), Oldenburg (2016) y Pulido (1997) muestran cómo conviven y generan diferentes conflictos, en estudiantes y docentes, los diversos significados del concepto de diferencial que se presentan de forma explícita o implícita en los diferentes libros de textos de cálculo, física, química, ingeniería, etc.
Un aspecto importante del concepto de diferencial que destaca Gómez (2019) es la problemática de la representación simbólica y su utilización en relación con los conceptos de derivada, integral y ecuaciones diferenciales, porque la diferencial aparece en las expresiones dy = 𝑓´(x). dx, 
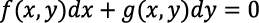 ,
, 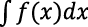 . Por ejemplo, Ely (2021) plantea que, en los libros de textos actuales, una diferencial no se puede escribir de manera significativa por sí misma, sino que solo adquiere significado cuando se la fusiona con otras notaciones, como
. Por ejemplo, Ely (2021) plantea que, en los libros de textos actuales, una diferencial no se puede escribir de manera significativa por sí misma, sino que solo adquiere significado cuando se la fusiona con otras notaciones, como 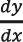 donde simboliza un lenguaje de código para representar
donde simboliza un lenguaje de código para representar 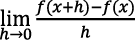 más que un cociente de cantidades.
más que un cociente de cantidades.
Indicadores específicos de las relaciones, procesos y conflictos de la idoneidad epistémica para el estudio de la diferencial
|
Componentes |
Indicadores |
|
Relaciones |
-Se identifican y articulan los diversos significados de diferencial según los objetos matemáticos (problemas, definiciones, proposiciones etc.) el nivel de generalización y formalización de los objetos intervinientes. -Se proponen situaciones para establecer relaciones entre la diferencial con otros conceptos, como derivada |
|
Procesos |
Comunicación-argumentación |
|
-Se debería tener en cuenta la diversidad de procesos (problematización, representación, definición, generalización, modelización, …) de los cuales emergen los objetos que intervienen en las prácticas matemáticas. Por ejemplo: El proceso de representación de las diferenciales mediante expresiones simbólicas como dx, dy, d𝑓 y mediante gráficos como la linealización de una curva. |
|
|
Modelización |
|
|
-Se plantean situaciones que permitan al estudiante utilizar modelos matemáticos para representar y comprender relaciones donde interviene la diferencial. Por ejemplo, problemas de velocidad instantánea, desintegración radiactiva, etc. (López-Gay et al., 2018). -Se plantean situaciones en las que la modelización es utilizada para comprender y establecer relaciones en el estudio de diversos fenómenos que involucran cambios infinitamente pequeños (Leibniz), o cambios considerados como variables que tiene límite cero (Cuachy), o al buscar la mejor aproximación local o estimación lineal de una curva en un punto (Fréchet) de diversos fenómenos de estudio provenientes de las matemáticas, la física, química, biología, economía y las ingenierías (López-Gay et al., 2015). |
|
|
Conceptualización |
|
|
-Se promueven situaciones donde los estudiantes tengan oportunidad de describir, explicar, hacer generalizaciones y conjeturas sobre la diferencial como cantidades de magnitudes infinitamente pequeñas (diferencial de Leibniz), como una variable que tiene límite cero (diferencial de Cauchy), como la mejor aproximación local de la curva (diferencial de Fréchet). |
|
|
Conflictos epistémicos |
-Se deberían evitar discordancias entre los significados de la diferencial con los correspondientes a la institución de referencia, por ejemplo, en las carreras de matemática, física, ingeniería y ciencias experimentales. -Se debería tener cuidado con la presentación de los objetos matemáticos relacionados con la diferencial para evitar errores, contradicciones y ambigüedades. -Se debería tener en cuenta que los símbolos y expresiones que involucran a la diferencial varían su significado según los contextos de uso y al estar relacionados con otros conceptos como derivada, integral y ecuaciones diferenciales, es importante dejar en claro cuál es el sentido de su uso. Por ejemplo: dy = 𝑓´(x). dx, -Se considera necesario generar instancias de reflexión sobre la diferencia en la consideración de las diferenciales como cantidad infinitamente pequeñas o como variables cuyo límite tiende a cero. -Se considera oportuno propiciar espacios para que los estudiantes compartan sus interpretaciones y sentidos en relación con para qué se usan las diferenciales en la resolución de las situaciones problemas. |
Nota: Fuente propia de la investigación.
La faceta cognitiva involucra el conocimiento didáctico-matemático sobre cómo los estudiantes aprenden, razonan y entienden las matemáticas y cómo progresan en su aprendizaje (Godino, Giacomone, Batanero y Font, 2017; Pino-Fan y Godino, 2015).
El aprendizaje es considerado desde el EOS como las prácticas personales que presentan estudiantes al resolver una tarea; su análisis permite al profesor comprender la configuración de prácticas, objetos y procesos que moviliza el estudiante. En la medida en que estas prácticas personales se correspondan con los significados institucionales parciales identificados previamente, el aprendizaje tendrá mayor grado de idoneidad cognitiva.
Relaciones: sabiendo que los significados parciales no están aislados entre sí, es importante que los estudiantes puedan establecer conexiones entre los diferentes significados del diferencial, conexiones entre los diferentes objetos matemáticos y entre sus correspondientes significados.
Procesos: teniendo en cuenta que el concepto de diferencial emerge de diversas situaciones-problemas del campo de las matemáticas y las ciencias experimentales, se considera importante que el estudiante pueda desarrollar la competencia matemática que le permita modelizar fenómenos de cambios.
Conocimientos previos: esta componente valora si se especifican los conceptos y competencias que se consideran necesarios para el estudio de la diferencial, con el propósito de que los estudiantes puedan establecer relaciones adecuadas entre los distintos contenidos y realizar un uso competente de estos mismos. Por ejemplo, Frank y Thompson (2021) plantean que los estudiantes, en sus estudios de bachillerato o precálculo, necesitan estudiar los significados de los conceptos de cambios y variaciones de cambios en los valores de una función, para tener mayores oportunidades de comprender, en los primeros cursos de cálculo, los significados de tasa de cambio y sus aplicaciones.
Conflictos cognitivos: varias investigaciones han reportado que estudiantes y docentes presentan diversas dificultades en relación con los usos de las diferenciales. Hu y Rebello (2013) plantean que el uso de los símbolos matemáticos, como la diferencial dx, dy, genera muchas dificultades para estudiantes de física porque depende del contexto de uso, ya que los diferenciales pueden representar una cantidad infinitesimal o un cambio infinitesimal de una cantidad física (Jones, 2013; 2015; Von Korff y Rebello, 2014). Además, el uso de la diferencial en relación con otros conceptos, plantea dificultades en los significados que entran en juego en la resolución de problemas (García Jiménez, 2018). Como se presenta en López-Gay y Martínez-Torregrosa (2005), en el discurso de estudiantes y docentes en formación entran en conflicto los significados de la diferencial y de la derivada, principalmente por las interpretaciones y ambigüedades que se originan en la utilización del símbolo diferencial. En los procesos de significación e interpretación del concepto de la integral definida se genera un conflicto cognitivo cuando el estudiante tiene que comprender al dx en la expresión 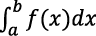 como lo estudia Burgos et al. (2021), Ely (2017) y Jones (2013; 2015).
como lo estudia Burgos et al. (2021), Ely (2017) y Jones (2013; 2015).
Indicadores específicos de idoneidad cognitiva en el estudio de la diferencial
|
Componentes |
Indicadores |
|
Significados personales (Aprendizajes) |
-Se debería conseguir que los significados personales de estudiantes se correspondan con los significados institucionales pretendidos, implementados y evaluados (ver, por ejemplo, Ramírez, Ibarra y Pino-Fan, 2020). -La evaluación de los aprendizajes debería utilizarse para mejorar el proceso de instrucción teniendo en cuenta las características personales, los niveles de comprensión y competencia que pueden desarrollar los estudiantes. |
|
Relaciones (conexiones) |
-Se debería proponer experiencias (situaciones, ejemplos, explicaciones…) que promuevan un aprendizaje de tipo relacional, de manera que permitan valorar si el estudiante establece relaciones o conexiones entre los significados de diferencial, sus sentidos, sus representaciones y contextos de uso. -Se plantean situaciones que permiten distinguir y relacionar la diferencial con la derivada, el límite, la integral y las ecuaciones diferenciales. Por ejemplo: velocidad instantánea, cálculo de la masa de una lámina, cambio total de la masa, etc. |
|
Procesos |
-Se debe tener en cuenta la competencia del estudiante para implementar procesos matemáticos en relación con la diferencial (modelización, generalización, conceptualización, resolución o planteamiento de problemas, prueba, representación, etc.) y metacognitivos (reflexión sobre los propios procesos de pensamiento matemático). |
|
Conocimientos previos (se tienen en cuenta los mismos elementos que para la idoneidad epistémica) |
-Se analiza que los estudiantes tienen los conocimientos previos y necesarios para abordar el estudio del diferencial, entre ellos: cantidad, variable, función, pendiente, variación, acumulación, entre otros que dependen de la complejidad ontosemiótica del significado parcial del diferencial que se pretende estudiar. -El profesor planifica situaciones problemas (p.e., aproximación o estimación lineal, pronóstico lineal, razón de cambio, tasas, velocidad, desintegración radiactiva, cálculo del área de un círculo, variación, cambio y acumulación total de la masa, optimización, etc.) que promueven la modelización en diversos contextos y permiten comprender la riqueza de procesos que emergen en el estudio de la diferencial. -Se utilizan diferentes registros apropiados para la representación de información, como gráficos, tablas, ecuaciones, expresiones simbólicas, etc. |
|
Diferencias individuales |
-Se debería tener en cuenta en el proceso instruccional las diferencias individuales de los estudiantes en sus conocimientos previos y estilos de aprendizaje en el proceso de estudio de la diferencial. -Se incluyen actividades de ampliación, refuerzo, contraejemplos y analogías. Por ejemplo, plantear la discusión sobre el uso de los términos: cantidad pequeña, cambio infinitamente pequeño, infinitesimal, variación infinitesimal, porción infinitesimal, aproximación, estimación lineal, error, entre otros, en relación con los significados de la diferencial. -Se promueve el acceso, el logro y apoyo de todos los estudiantes. |
|
Conflictos cognitivos |
-El proceso de instrucción debería abordar y clarificar los diferentes significados de la diferencial teniendo en cuenta las dificultades que se presentan según el contexto de uso, las expresiones simbólicas utilizadas y las interconexiones con otros conceptos como límite, derivada, integrales y ecuaciones diferenciales. -Se valora el error y la confusión en relación con las interpretaciones o sentidos del diferencial como fuente de aprendizaje. |
Nota: Fuente propia de la investigación. Adaptado de Godino, Batanero, Burgos y Gea (2021)
En esta faceta se valora la situación afectiva del sujeto que está frente a la resolución de cualquier problema matemático, ya que no solo pone en juego prácticas operativas y discursivas para dar una respuesta al problema, sino que también moviliza actitudes, creencias, emociones y valores que condicionan, en mayor o menor grado, la respuesta cognitiva requerida (Godino, 2013).
Beltrán-Pellicer y Godino (2020) y Grootenboer y Marshman (2016) plantean que existe un cierto consenso en la comunidad científica respecto a las componentes del dominio afectivo en la educación matemática, donde destacan las emociones, actitudes, creencias y valores. Por tales motivos, consideramos que es necesario tener en cuenta estas componentes para la valoración de la faceta afectiva para el estudio de la diferencial de una función.
Las componentes del dominio afectivo están presentes en todo el proceso de estudio (antes, durante y después), como sugieren Grootenboer y Marshman (2016) al mencionar que el afecto influye en el aprendizaje de las matemáticas, pero también los estudiantes desarrollan creencias, actitudes y emociones a medida que participan de las experiencias del aula.
Emociones: se entiende que son los cambios que se producen rápidamente y que son experimentados de manera consciente o que ocurren preconsciente o inconscientemente durante el momento de resolver una tarea y pueden variar de leves a intensas. Cabe destacar que las emociones, como una práctica afectiva, se manifiestan de manera local y contextual (Beltrán-Pellicer y Godino, 2020). En este componente se valorará que los contenidos estén vinculados con los problemas sociales o la vida social de los estudiantes, como así también que incluyan aspectos motivacionales y que se generen espacios para potenciar la autoestima y eviten el rechazo hacia las matemáticas (Castillo, Burgos y Godino, 2022).
Actitudes: se considera que “describen orientaciones o predisposiciones hacia ciertos conjuntos de sensaciones emocionales (positivas o negativas), en contextos particulares (matemáticos)” (Beltrán-Pellicer y Godino, 2020, p. 6). Será importante valorar si se plantean situaciones que motivan a los estudiantes en la participación de las actividades, en favorecer la argumentación en situaciones de igualdad y fomentar una actitud de flexibilidad hacia la exploración de ideas y caminos de resolución de problemas.
Creencias: “implican la atribución de algún tipo de verdad o validez externa al sistema de proposiciones u otras configuraciones cognitivas. Las creencias suelen ser muy estables, en gran parte cognitivas y estructuradas” (Beltrán-Pellicer y Godino, 2020, p. 6). En este componente se valoran las creencias sobre las matemáticas, su enseñanza y aprendizaje, como así también las creencias en torno a la formación de profesores, físicos e ingenieros en relación con el cálculo.
Valores: incluyen componentes éticos y morales, y se entienden como “verdades personales y aspectos apreciados por los individuos” (Castillo et al., 2022, p. 15). En este componente se valorarán los sistemas de valores que ayudan a motivar las decisiones.
Por ejemplo, en la investigación de Moreno y Azcárate (2003) estudian cómo influyen las creencias de los profesores sobre la enseñanza y el aprendizaje de las ecuaciones diferenciales, donde plantean que las creencias, actitudes y los sistemas de valores entran en juego en la toma de decisiones en relación con las estrategias didácticas, gestión de la clase, concepciones sobre la enseñanza, competencia matemática de estudiantes, entre otras.
Esta faceta se caracteriza por la valoración de la negociación de los significados que se deberían generar en un proceso instruccional; es decir, se estudia el grado en que los modos de interacción entre docente, estudiantes y entre estudiantes permiten identificar y resolver potenciales conflictos semióticos, favorecer el aprendizaje autónomo y el desarrollo de competencias comunicativo-argumentativas (Godino, 2013).
Interacción docente-estudiante: en esta componente se valora si las configuraciones didácticas planificadas posibilitan una presentación clara, ordenada y adecuada de los conceptos claves en relación con la diferencial. Además, si se propicia situaciones-problemas que permitan establecer relaciones con los otros conceptos del cálculo, como el límite, derivada e integral, de manera que se empleen recursos retóricos y argumentativos para reconocer y resolver potenciales conflictos de significados del diferencial.
Interacciones entre estudiantes: las configuraciones didácticas planificadas deberían contemplar momentos de diálogo, comunicación y debate entre estudiantes, y generar situaciones donde tengan que convencer a sus pares sobre la validez de sus afirmaciones y conjeturas empleando argumentos matemáticos.
Autonomía: se valora si las situaciones problemas contemplan momentos donde los estudiantes tengan que asumir la responsabilidad del estudio desarrollando una autonomía para enfrentarse a diferentes y nuevos problemas.
Evaluación formativa: se considera la evaluación continua a lo largo de todo el desarrollo de la trayectoria didáctica y no únicamente al final, ya que la progresión en el aprendizaje tiene lugar en la medida que el estudiante se apropia de los diversos significados, reconoce y comprende la trama de objetos matemáticos implicados en ellos (Godino y Burgos, 2020). Por tales motivos, se considera estas prácticas personales como indicadores explícitos para que el profesor pueda valorar las relaciones de sus estudiantes con los objetos.
Se tendrá mayor idoneidad interaccional si se consideran formatos de interacción de tipo dialógica y colaborativas, sobre los de tipo magistral e individual (Godino, Font, Wilhelmi y De Castro, 2009). Además, a partir de esta valoración es posible determinar intervenciones más adecuadas durante el proceso de enseñanza y aprendizaje para mejorar la apropiación de los significados del concepto de diferencial.
Esta faceta valora el grado de disponibilidad y adecuación de los recursos tecnológicos, materiales y temporales para el desarrollo óptimo del proceso de enseñanza y aprendizaje (Godino et al., 2021).
Recursos materiales: esta componente valora el uso de diferentes tipos de recursos manipulativos, audiovisuales e informáticos que permitan generar buenas situaciones-problemas que potencien el desarrollo de la competencia matemática de los estudiantes. Los recursos tecnológicos, como calculadoras, sistemas de cálculo algebraico simbólico, software de geometría dinámica, graficadores, hojas de cálculo, applets y dispositivos de presentación interactiva, tienen un gran peso en la enseñanza del cálculo diferencial (Garcés-Córdova y Font, 2022), ya que permiten, entre otras cuestiones, estudiar modelos concretos y potenciar la visualización. Sin embargo, Hitt (2014) advierte que el uso de herramientas tecnológicas no debe ser destinado exclusivamente a graficar funciones, ya que se pierde la riqueza que estas aportan a los procesos de modelación matemática. Se destaca también la importancia y el impacto educativo mediante la manipulación de objetos físicos y su articulación con entornos tecnológicos (Hitt, 2014).
Condiciones ambientales: las condiciones del aula y la distribución de estudiantes deben ser adecuadas para llevar a cabo el proceso instruccional del estudio del diferencial pretendido.
Tiempo de enseñanza y aprendizaje: resulta importante valorar si la distribución del tiempo es idónea en cuanto a la organización de los momentos de enseñanza, las experiencias de aprendizajes, los momentos de trabajo presencial y no presencial, y la dedicación a los contenidos según su dificultad para los estudiantes. Se recomienda dedicar tiempo de discusión al fenómeno físico mediante la modelización, sin limitarla a aspectos netamente algebraicos (Hitt, 2014).
Esta faceta valora el grado en que una propuesta, una acción formativa o un plan es adecuado dentro del entorno en que el que se realiza. Por entorno se entiende todo lo que está fuera del aula, pero condiciona la actividad (y, además, es condicionado por ella) que se desarrolla en esta. Condiciones que provienen de la sociedad, la escuela, la pedagogía, la didáctica de las matemáticas, la investigación, etc. (Godino, 2013).
Adaptación al currículo: en qué medida la propuesta de enseñanza se corresponde con los diseños curriculares, ya sean profesores de matemáticas o física, licenciados en matemáticas, ingenieros, economistas, etc.
Apertura hacia la innovación didáctica: se valora si se tienen en cuenta los resultados de las investigaciones en didáctica del cálculo y el uso de las nuevas tecnologías, ya que existe una tendencia actual en la enseñanza del cálculo donde los recursos tecnológicos ocupan un lugar importante en la clase de matemáticas (Hitt, 2017). Estos recursos pueden ser softwares específicos de matemáticas o videos que simulan los fenómenos en estudio; su uso es importante porque permiten abordar la modelización matemática, el tratamiento y la conversión entre los diferentes registros de representación semiótica y la integración de varias disciplinas. Por ejemplo, Thompson y Harel (2021) proponen el uso de animaciones para estudiar las variaciones, sus cambios y acumulación.
Adaptación socio-profesional y cultural: valora si la propuesta de estudio del diferencial contribuye a la formación socio-profesional de los estudiantes. Es decir, si está orientada hacia el estudio de la diferencial en el contexto de la ingeniería o si se adapta al campo profesional de un futuro profesor de matemáticas o física, según la carrera.
Educación en valores: la propuesta de enseñanza debería evitar la trasmisión de estereotipos, elementos racistas, sexistas, discriminatorios, etc. Tendría que fomentar los valores democráticos como el respeto por la diversidad, la tolerancia, la cooperación, el respeto por las ideas de sus pares, y el pensamiento crítico.
Por último, la componente conexiones intra e interdisciplinares valora si la propuesta didáctica permite establecer relaciones entre la diferencial con los conceptos de cantidad, variable, función, límite, derivada, integrales y ecuaciones diferenciales. Además, valora las conexiones con los conceptos de razón de cambio, tasa de variación, velocidad, aceleración, densidad variable, cambio total de una variable, costo marginal, entre otros temas de las ingenierías y las ciencias experimentales.
En este artículo, se ha descrito la elaboración de una Guía de valoración de la idoneidad didáctica para procesos de estudio del concepto de diferencial, fundamentada tanto en las sugerencias de la bibliografía científica como en la noción de idoneidad didáctica propuesta por el EOS. Los indicadores de las facetas epistémica, cognitiva, afectiva, interaccional, mediacional y ecológica han sido particularizados para el estudio de la diferencial a partir del análisis de los resultados de diversas investigaciones didácticas sobre los distintos significados, sobre qué matemáticas se deberían enseñar y aprender, sobre los contextos de aplicación, circunstancias y recursos disponibles. El desafío radica, precisamente, en lograr un equilibrio entre el grado de adecuación de cada una de las idoneidades (Godino, 2021) para mejorar los procesos de enseñanza y aprendizaje de la diferencial.
La guía debe entenderse como una herramienta para orientar la reflexión del profesor en el diseño, implementación y evaluación de procesos de estudio, con el propósito de lograr la optimización de los procesos de enseñanza y aprendizaje en torno a la diferencial (Godino, 2021; Pino-Fan y Parra-Urrea, 2021). En este sentido, Malet, Giacomone y Repetto (2021) resaltan la importancia que tiene la elaboración de guías específicas de valoración como herramienta de reflexión sobre la propia práctica docente. Además, reclaman la necesidad de seguir con esta línea cubriendo diversos contenidos matemáticos.
Es importante destacar que esta guía de valoración puede ser utilizada no solo para las clases de matemáticas, sino también para clases que estén en estrecha relación con el concepto de diferencial, como clases de física, ingeniería y las ciencias experimentales.
Trabajo realizado en el marco de los proyectos PFID-FID-2021-45 (Panamá), PID2021-122326OB-I00 (España), 16Q1706-PI y 16Q1746-TI (FCEQyN – UNaM, Argentina) y el Proyecto de Investigación Fondecyt Regular 1200005 financiado por la Agencia Nacional de Investigación y Desarrollo (ANID) de Chile.
Los autores declaran no tener algún conflicto de interés.
Declaración de la contribución de los autores
Todos los autores afirmamos que se leyó y aprobó la versión final de este artículo.
El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: M.A.V. 40 %, B.G. 30 % y L.R.P.F. 30 %.
Declaración de disponibilidad de los datos
Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente [M.A.V.], previa solicitud razonable.
Alibert, D., & Legrand, M. (1989). Procedures differentielles et integrales aun niveau du premier cycle universitaire – une mise au point. En Procedures différentielles dans les enseignements de mathematiques et de physique au niveau du premier cycle universitaire (Annexe VII). Université Paris 7: IREM et LDPES.
Araya, D., Pino-Fan, L. R., Medrano, I. G., & Castro, W. F. (2021). Epistemic criteria for designing limit tasks on a real variable function. Bolema: Boletim de Educação Matemática, 35(69), 179-205. https://doi.org/10.1590/1980-4415v35n69a09
Arcos, I. (2004). Rigor o entendimiento, un viejo dilema en la enseñanza de las matemáticas: El caso del cálculo infinitesimal. Tiempo de Educar, 5(10), 77-110.
Artigue, M. (1995). La enseñanza de los principios del cálculo: Problemas epistemológicos, cognitivos y didácticos. En P. Gomez (Ed.), Ingeniería didáctica en educación matemática. Un esquema para la investigación y la innovación y el aprendizaje de las matemáticas (pp. 97-140). Una empresa docente y Grupo editorial iberoamerica.
Artigue, M., Menigoux, J., & Viennot, L. (1990). Some aspects of students’ conceptions and difficulties about differentials. European Journal of Physics, 11(5), 262-267. https://doi.org/10.1088/0143-0807/11/5/002
Badillo, E., Font, V., & Azcárate, C. (2005). Conflictos semióticos relacionados con el uso de la notación incremental y diferencial en libros de física y de matemática del bachillerato. Enseñanza de las Ciencias, (Extra), 1-6.
Beltrán-Pellicer, P., & Godino, J. D. (2020). An onto-semiotic approach to the analysis of the affective domain in mathematics education. Cambridge Journal of Education, 50(1), 1-20. https://doi.org/10.1080/0305764X.2019.1623175
Beltran-Pellicer, P., Godino, J. D., & Giacomone, B. (2018). Elaboración de indicadores específicos de idoneidad didáctica en probabilidad: Aplicación para la reflexión sobre la práctica docente. Bolema: Boletim de Educação Matemática, 32(61), 526-548. https://doi.org/10.1590/1980-4415v32n61a11
Bos, H. J. M. (1974). Differentials, higher-order differentials and derivatives in the Leibnizian calculus. Archive for history of exact sciences, 14(1), 1-90. https://doi.org/10.1007/BF00327456
Breda, A., Font, V., & Pino-Fan, L. R. (2018). Criterios valorativos y normativos en la didáctica de las matemáticas: El caso del constructo idoneidad didáctica. Bolema: Boletim de Educação Matemática, 32(60), 255-278. https://doi.org/10.1590/1980-4415v32n60a13
Burgos, M., Bueno, S., Pérez, O., & Godino, J. (2021). Onto-semiotic complexity of the definite integral. Journal of Research in Mathematics Education, 10(1), 4-40. http://dx.doi.org/10.17583/redimat.2021.6778
Castro, W. F., & Pino-Fan, L. R. (2021). Comparing the didactic-mathematical knowledge of derivative of in-service and pre-service teachers. Acta Scientiae, 23(3), 34-95. https://doi.org/10.17648/acta.scientiae.5842
Cauchy, A. L. (1821). Cours d’analyse de l’ecole royale polytechnique. L’Imprimerie Royale, ETH Library Zurich. https://doi.org/10.3931/e-rara-26185
Cauchy, A. L. (1823). Résumé des leçons données à l’ecole royale polytechnique sur le calcul infinitésimal. L’Imprimerie Royale, ETH Library Zurich. https://doi.org/10.3931/e-rara-25962
Castillo, M. J. C., Burgos, M., & Godino, J. D. (2022). Elaboración de una guía de análisis de libros de texto de matemáticas basada en la teoría de la idoneidad didáctica. Educação e Pesquisa, 48, e238787. https://doi.org/10.1590/S1678-4634202248238787esp
Cohen, L., Manion, L., & Morrison, K. (2007). Research methods in education. Routledge. https://doi.org/10.4324/9780203029053
Cordero-Osorio, F. (1991). Taking a differential element: its formation and meaning in the didactic discourse of calculus. International Journal of Mathematical Education in Science and Technology, 22(6), 869-872. https://doi.org/10.1080/0020739910220601
Dray, T., & Manogue, C. A. (2010). Putting differentials back into calculus. College Mathematics Journal, 41(2), 90-100. https://doi.org/10.4169/074683410X480195
Edwards, C. H. (1979). The historical development of the calculus. Springer-Verlag. https://doi.org/10.1007/978-1-4612-6230-5
Ely, R. (2017). Definite integral registers using infinitesimals. The Journal of Mathematical Behavior, 48, 152-167. https://doi.org/10.1016/j.jmathb.2017.10.002
Ely, R. (2021). Teaching calculus with infinitesimals and differentials. ZDM Mathematics Education, 53, 591-604. https://doi.org/10.1007/s11858-020-01194-2
Frank, K., & Thompson, P. W. (2021). School students’ preparation for calculus in the United States. ZDM Mathematics Education, 53, 549-562. https://doi.org/10.1007/s11858-021-01231-8
Font, V., Pino-Fan, L. R., & Breda, A. (2020). Una evolución de la mirada sobre la complejidad de los objetos matemáticos. Revista Paradigma, 41, 107-129. https://doi.org/10.37618/PARADIGMA.1011-2251.2020.p107-129.id846
Garcés-Córdova, W., & Font-Moll, V. (2022). Criterios que guían la práctica de los profesores de matemáticas en cursos de ciencias básicas de ingeniería. Uniciencia, 36(1), 1-19. https://doi.org/10.15359/ru.36-1.5
García Jiménez, V. (2018). Resignificar la diferencial en y con prácticas de modelación. Revista Latinoamericana de Etnomatemática, 11(1), 139-178.
Godino, J. D. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 11, 111-132.
Godino, J. D. (2021). De la ingeniería a la idoneidad didáctica en la enseñanza de las matemáticas. Revemop, 3, e202129. https://doi.org/10.33532/revemop.e202129
Godino, J. D., Batanero, C., Burgos, M., & Gea, M. M. (2021). Uma perspectiva ontosemiótica dos problemas e métodos de pesquisa em educação matemática. Revemop, 3, e202107. https://doi.org/10.33532/revemop.e202107
Godino, J. D., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM Mathematics Education, 39, 127-135. https://doi.org/10.1007/s11858-006-0004-1
Godino, J. D., Batanero, C., & Font, V. (2020). El enfoque ontosemiótico: Implicaciones sobre el carácter prescriptivo de la didáctica. Revista Chilena de Educación Matemática, 12(2), 3–15. https://doi.org/10.46219/rechiem.v12i2.25
Godino, J. D., Batanero, C., Rivas, H., & Arteaga, P. (2013). Componentes e indicadores de idoneidad de programas de formación de profesores en didáctica de las matemáticas. Revista Eletrônica de Educação Matemática, 8(1), 46-74. https://doi.org/10.5007/1981-1322.2013v8n1p46
Godino, J. D., & Burgos, M. (2020). ¿Cómo enseñar las matemáticas y ciencias experimentales? Resolviendo el dilema entre transmisión e indagación. Revista Paradigma, 41, 80-106. https://doi.org/10.37618/PARADIGMA.1011-2251.2020.p80-106.id872
Godino, J. D., Font, V., Wilhelmi, M. R., & De Castro, C. (2009). Aproximación a la dimensión normativa en didáctica de las matemáticas desde un enfoque ontosemiótico. Enseñanza de las Ciencias, 27(1), 59-76. https://doi.org/10.5565/rev/ensciencias.3663
Godino, J. D., Giacomone, B., Batanero, C., & Font, V. (2017). Enfoque ontosemiótico de los conocimientos y competencias del profesor de matemáticas. Bolema: Boletim de Educação Matemática, 31(37), 90-113. https://doi.org/10.1590/1980-4415v31n57a05
Gómez, A. (2019). A look to differential. Journal of Physics: Conference Series. V International Conference Days of Applied Mathematics, 1414, 1-7. https://doi.org/10.1088/1742-6596/1414/1/012001
Grootenboer, P., & Marshman, M. (2016). El dominio afectivo, las matemáticas y la educación matemática. En Matemáticas, afecto y aprendizaje. Springer. https://doi.org/10.1007/978-981-287-679-9_2
Harel, G. (2021). The learning and teaching of multivariable calculus: a DNR perspective. ZDM Mathematics Education 53, 709-721. https://doi.org/10.1007/s11858-021-01223-8
Hitt, F. (2014). Nuevas tendencias en la enseñanza del cálculo: La derivada en ambientes TICE. AMIUTEM, 2(2), 1-19.
Hitt, F. (2017). El aprendizaje del cálculo y nuevas tendencias en su enseñanza en el aula de matemáticas. ECO MATEMATICO, 8, 6-15. https://doi.org/10.22463/17948231.1374
Hu, D., & Rebello, N. S. (2013). Understanding student use of differentials in physics integration problems. Physical Review Special Topics - Physics Education Research, 9(2), 1-14. https://doi.org/10.1103/PhysRevSTPER.9.020108
Jones, S. R. (2013). Understanding the integral: Students’ symbolic forms. The Journal of Mathematical Behavior, 32(2), 122-141. https://doi.org/10.1016/j.jmathb.2012.12.004
Jones, S. R. (2015). Areas, anti-derivatives, and adding up pieces: definite integrals in pure mathematics and applied science contexts. Journal of Mathematical Behavior, 38, 9-28. https://doi.org/10.1016/j.jmathb.2015.01.001
Keisler, H. J. (2000). Elementary calculus. An infinitesimal approach. University of Wisconsin.
Kitcher, P. (1984). The nature of mathematical knowledge. Oxford University Press. https://doi.org/10.1093/0195035410.001.0001
Kleiner, I. (2012). History of the infinitely small and the infinitely large in calculus, with remarks for the teacher. In Excursions in the History of Mathematics (pp. 67-101). Birkhäuser. https://doi.org/10.1007/978-0-8176-8268-2_4
López-Gay, R. L. V. (2001). La introducción y utilización del concepto de diferencial en la enseñanza de la física. Análisis de la situación actual y propuesta para su mejora [Tesis doctoral, Universidad Autónoma de Madrid, España].
López-Gay, R., & Martínez Torregrosa, J. (2005). Identificación de obstáculos para un uso con comprensión del cálculo diferencial en física. Enseñanza de las ciencias, (extra), 1-5.
López-Gay, R., Sáez, J. M., & Torregrosa, J. M. (2015). Obstacles to mathematization in physics: The case of the differential. Science & Education, 24(5-6), 591-613. https://doi.org/10.1007/s11191-015-9757-7
López-Gay, R., Martínez-Torregrosa, J., Jiménez Liso, M., Martínez Chico, M., & Gil Martínez, E. (2018). Significado y uso de la diferencial. Ayudando a conectar el mundo físico y matemático. Uno. Revista de Didáctica de las Matemáticas, (81), 41-44.
Malet, O., Giacomone, B., & Repetto, A. M. (2021). Idoneidad didáctica como herramienta metodológica: Desarrollo y contextos de uso. Revemop, 3, e202110. https://doi.org/10.33532/revemop.e202110
Martínez-Planell, R., & Trigueros, M. (2021). Multivariable calculus results in different countries. ZDM Mathematics Education, 53, 695-707. https://doi.org/10.1007/s11858-021-01233-6
Martínez-Torregrosa, J., López-Gay, R., & Gras-Martí, A. (2006). Mathematics in physics education: scanning historical evolution of the differential to find a more appropriate model for teaching differential calculus in physics. Science & Education, 15(5), 447-462. https://doi.org/10.1007/s11191-005-0258-y
Martínez-Torregrosa, J., López-Gay, R., Gras-Martí., A., & Torregrosa-Gironés, G. (2002). La diferencial no es un incremento infinitesimal. Evolución del concepto de diferencial y su clarificación en la enseñanza de la física. Enseñanza de las Ciencias, 20(2), 271-283. https://doi.org/10.5565/rev/ensciencias.3970
Martínez Uribe, A., Pluvinage, F., & Montaño Zetina, L. M. (2017). El concepto de la derivada en el contexto de la enseñanza de la física, recursos para el uso de diferenciales y las tecnologías de información y comunicación. El Cálculo y su Enseñanza, Enseñanza de las Ciencias y la Matemática, 8, 1-17.
Moreno, M. M., & Azcárate C. (2003). Concepciones y creencias de los profesores universitarios de matemáticas acerca de la enseñanza de las ecuaciones diferenciales. Enseñanza de las Ciencias: Revista de investigación y experiencias didácticas, 21(2), 265-80. https://doi.org/10.5565/rev/ensciencias.3930
Oldenburg, R. (2016). Differentiale als prognosen. Journal für Mathematik-Didaktik, 37, 55-82. https://doi.org/10.1007/s13138-016-0096-2
Orton, A. (1983). Students’ understanding of differentiation. Educational Studies in Mathematics, 14, 235-250. https://doi.org/10.1007/BF00410540
Pino-Fan, L. R., & Godino, J. D. (2015). Perspectiva ampliada del conocimiento didáctico-matemático del profesor. Paradígma, 36(1), 87-109.
Pino-Fan, L. R., Godino, J. D., & Font, V. (2011). Faceta epistémica del conocimiento didáctico-matemático sobre la derivada. Educação Matemática Pesquisa, 13(1), 141-178.
Pino-Fan, L., & Parra-Urrea, Y. (2021). Criterios para orientar el diseño y la reflexión de clases sobre funciones ¿Qué nos dice la literatura científica? UNO. Revista de Didáctica de las Matemáticas, 91, 45-54.
Pulido, R. (1997). Un estudio teórico de la articulación del sable matemático en el discurso escolar: La transposición didáctica del diferencial en la física y la matemática escolar [Tesis doctoral, Cinvestav, México].
Pulido, R. (2010). La enseñanza de los diferenciales en las escuelas de ingeniería desde un enfoque socioepistemológico. Relime: Revista Latinoamericana de Investigación en Matemática Educativa, 13(4-I), 85-97.
Robinson, A. (1966). Non-standard analysis. North-Holland Publishing Company Amsterdam.
Ramírez, R., Ibarra, S., & Pino-Fan, L. (2020). Prácticas evaluativas y significados evaluados por profesores del bachillerato mexicano sobre la noción de ecuación lineal. Educación Matemática, 32(2), 69-98. https://doi.org/10.24844/EM3202.03
Ruz, F., Molina-Portillo, E., & García, J. M. C. (2019). Guía de valorización de la idoneidad didáctica de procesos de instrucción en didáctica de la estadística. Bolema: Boletim de Educação Matemática, 33(63), 135-154. https://doi.org/10.1590/1980-4415v33n63a07
Tall, D. O. (1981). Comments on the difficulty and validity of various approaches to the calculus. For the Learning of mathematics, 2(2), 16-21.
Taylor, A. (1974). The differential: nineteenth and twentieth century developments. Archive for history of exact sciences, 12(4), 355-383. https://doi.org/10.1007/BF01307177
Thompson, P.W., & Harel, G. (2021). Ideas foundational to calculus learning and their links to students’ difficulties. ZDM Mathematics Education, 53, 507–519. https://doi.org/10.1007/s11858-021-01270-1
Valdivé, C., & Garbin, S. (2008). Estudio de los esquemas conceptuales epistemológicos asociados a la evolución histórica de la noción de infinitesimal. Relime: Revista Latinoamericana de Investigación en Matemática Educativa, 11(3), 413-450.
Von Korff, J., & Rebello, N. S. (2014). Distinguishing between change and amount infinitesimals in first-semester calculus-based physics. American Journal of Physics, 82(7), 695-705. https://doi.org/10.1119/1.4875175
Verón, M. A. (2020). Análisis ontosemiótico de los significados del concepto de diferencial [Tesis de Maestría, Universidad de Granada. España]. http://dx.doi.org/10.13140/RG.2.2.17929.16489
Verón, M. A., & Giacomone, B. (2021). Análise dos significados do conceito de diferencial de uma perspectiva ontosemiótica. Revemop, 3, e202109. https://doi.org/10.33532/revemop.e202109
*Autor para correspondencia
Manuel Alejandro Verón, ![]() alejandroveron@fceqyn.unam.edu.ar,
alejandroveron@fceqyn.unam.edu.ar, ![]() https://orcid.org/0000-0002-3160-1031
https://orcid.org/0000-0002-3160-1031
Belén Giacomone, ![]() belen.giacomone@unirsm.sm,
belen.giacomone@unirsm.sm, ![]() https://orcid.org/0000-0001-6752-2362
https://orcid.org/0000-0001-6752-2362
Luis Roberto Pino-Fan, ![]() luis.pino@ulagos.cl,
luis.pino@ulagos.cl, ![]() https://orcid.org/0000-0003-4060-7408
https://orcid.org/0000-0003-4060-7408
1 Departamento de Matemática. Universidad Nacional de Misiones, Posadas, Argentina.
2 Departamento de Economía, Ciencia y Derecho. Universidad de la República de San Marino, Dogana, San Marino.
3 Departamento de Ciencias Exactas. Universidad de Los Lagos, Osorno, Chile.
Guía de valoración de la idoneidad didáctica de procesos de estudio de la diferencial (Manuel Alejandro Verón • Belén Giacomone • Luis Roberto Pino-Fan) Uniciencia is protected by Attribution-NonCommercial-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0)
URL: www.revistas.una.ac.cr/uniciencia
Correo electrónico: revistauniciencia@una.cr

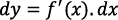



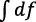



 ,
, 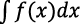 ;
;