Revista UNICIENCIA
Uniciencia Vol. 38(1), January-December, 2024
E-ISSN: 2215-3470
DOI: https://dx.doi.org/10.15359/ru.38-1.17

---

Proceso de instrucción de la derivada aplicado a estudiantes de Ingeniería Comercial en Chile

Instructional Process of the Derivative Applied in Business Engineering Students in Chile

Processo de instrução do derivado aplicado a estudantes de engenharia de negócios no Chile

Maritza Katherine Galindo Illanes1, Adriana Breda2*

Received: Aug/15/2023 • Accepted: Sep/20/2023 • Published: Jul/31/2024

Resumen [Objetivo] El objetivo de este artículo es presentar los resultados de la implementación de un diseño instruccional de enseñanza de la derivada para estudiantes universitarios de la carrera de Ingeniería Comercial en Chile. [Metodología] Las personas participantes del estudio son noventa estudiantes de la asignatura de Cálculo Aplicado a los Negocios de una universidad chilena. El diseño metodológico, basado en las herramientas del Enfoque Ontosemiótico del Conocimiento e Instrucción Matemáticos, considera diversas configuraciones epistémicas en las situaciones-problemas sobre tangentes, el cálculo de derivadas a partir de reglas de derivación, aplicaciones de la derivada para el cálculo de máximos y mínimos y análisis de gráficas de funciones. Además, integra las TIC en las diversas tareas. [Resultados] Los resultados indican que la propuesta instruccional de enseñanza de la derivada supera algunas de las dificultades de aprendizaje de los y las estudiantes, evidenciadas en diversas investigaciones. En particular, las dificultades del estudiantado de Ingeniería Comercial en torno a la concepción euclidiana de la recta tangente; la interpretación de la función “derivada” y su representación geométrica, la optimización de funciones económicas y la aplicación de la derivada a funciones marginales. [Conclusiones] Se concluye que el proceso de enseñanza y aprendizaje es eficaz, en el sentido de que se consigue el aprendizaje del alumnado de una carrera de ingeniería específica mediante la incorporación, en la instrucción, de diferentes configuraciones epistémicas de la derivada interconectadas, sus diferentes campos de problemas y las aplicaciones contextuales en su profesión, junto al uso de recursos TIC. Palabras clave: enseñanza de las matemáticas; derivada; proceso de instrucción; TIC; Enfoque Ontosemiótico; formación de ingenieros; Ingeniería Comercial. Abstract [Objective] The objective of this article is to present the results of the implementation of an instructional design for the teaching of the derivative for undergraduate students of Business Engineering in Chile. [Methodology] The participants in the study were ninety students of Applied Business Calculus at a Chilean university. The methodological design, based on the tools of the Ontosemiotic Approach to Mathematical Cognition and Instruction, consider various epistemic configurations in situations-problems concerning tangents, the calculation of derivatives from the rules for derivation, applications of the derivative for the calculation of maxima and minima, and analysis of graphs of functions. In addition, it integrates ICT into various activities. [Results] The results indicate that the instructional proposal for teaching the derivative overcomes some of students’ learning difficulties, as shown in various research studies. In particular, these include the difficulties that Business Engineering students have with the Euclidean conception of the tangent line, the interpretation of the derivative function and its geometric representation, the optimization of economic functions, and the application of the derivative to marginal functions. [Conclusions] It is concluded that the teaching and learning process is effective, in the sense that student learning for a specific engineering career is achieved by instruction that incorporates different interconnected epistemic configurations of the derivative, its different fields of problems, and contextual applications in their profession, together with the use of ICT resources. Keywords: Mathematics education; derivative; instructional process; ICT; Ontosemiotic Approach; engineering education; business engineering. Resumo [Objetivo] O objetivo deste artigo é apresentar os resultados da implementação de um desenho instrucional para o ensino da derivada para alunos de graduação em Engenharia de Negócios no Chile. [Metodologia] Os participantes do estudo são noventa alunos da disciplina de Cálculo Empresarial Aplicado de uma universidade chilena. O desenho metodológico, baseado nas ferramentas da Abordagem Ontossemiótica do Conhecimento e Instrução Matemática, considera diversas configurações epistêmicas nas situações-problemas sobre tangentes, cálculo de derivadas a partir de regras de derivadas, aplicações da derivada para o cálculo de máximos e mínimos e análise de gráficos de funções. Além disso, integra as TIC nas diversas tarefas. [Resultados] Os resultados indicam que a proposta instrucional para o ensino da derivada supera algumas das dificuldades de aprendizagem dos alunos, conforme evidenciado em várias pesquisa. Em particular, as dificuldades dos alunos de Engenharia de Negócios sobre a concepção euclidiana da reta tangente; sobre a interpretação da função “derivada” e sua representação geométrica, sobre a otimização de funções econômicas e a aplicação da derivada a funções marginais. [Conclusões] Conclui-se que o processo de ensino e aprendizagem é eficaz, no sentido de que a aprendizagem dos alunos em um curso de engenharia específico, é alcançada por meio da incorporação, na instrução, de diferentes configurações epistêmicas da derivada interconectadas, dos diferentes campos de problemas e das aplicações contextuais em sua profissão, juntamente ao uso de recursos de TIC. Palavras-chave: ensino de matemática; derivada; processo instrucional; TIC; Abordagem Ontossemiótica; educação em engenharia; engenharia de negócios.

Introducción

La derivada es fundamental en la formación de las personas profesionales en ingeniería, dado que la comprensión de este objeto matemático permite resolver una variedad de problemas relacionados con el campo de la ingeniería. Ese hecho, ha generado diversos estudios con relación con la complejidad de sus significados, sus múltiples representaciones, los procesos de enseñanza y aprendizaje, la idoneidad del significado de la derivada en los distintos currículos y los significados parciales en los textos universitarios de enseñanza para las ingenierías (Galindo Illanes y Breda, 2023b; Larios et al., 2021; Larios y Jiménez, 2022; Pino-Fan et al., 2016; Rodríguez-Nieto et al., 2022). Trabajar los distintos significados de un objeto matemático es un aspecto propuesto por el Enfoque Ontosemiótico del Conocimiento e Instrucción Matemáticos (EOS, en adelante) (Godino et al., 2007, 2019), para conseguir una mejor comprensión y competencia del estudiantado y para presentarles unas “buenas” matemáticas, lo cual plantea analizar la complejidad de los objetos matemáticos por medio de sus pluri significaciones (significados parciales).

Algunos estudios de la derivada en carreras de Ingeniería Comercial afirman tener presente la relación entre los procesos y conceptos económicos y matemáticos. En particular, se observa un amplio énfasis en los procesos de representación utilizados en el área de la microeconomía (Ballard y Johnson, 2004; Butler et al., 1994; García et al., 2006; Hey, 2005). También, por las dificultades en la interpretación de situaciones económicas debido a la débil comprensión de los significados matemáticos que las organizan (Ariza Cobos y Linares Ciscar, 2009).

En esta línea, este trabajo forma parte de una investigación más amplia que pretende profundizar en la comprensión de las futuras personas profesionales en ingeniería comercial acerca del objeto matemático derivada en el contexto chileno. Para conseguir dicho objetivo, se ha realizado un estudio en diferentes etapas.

La primera etapa fue un estudio diagnóstico, el cual reveló que el alumnado presenta dificultades relacionadas con: a) el concepto de función y la concepción euclidiana de la recta tangente; b) la construcción del significado de recta tangente como límite de rectas secantes; c) la interpretación de la función derivada y su representación geométrica; realizar operaciones para calcular la pendiente de una recta y d) operar con funciones (Galindo Illanes et al., 2022; Galindo Illanes y Breda, 2022b).

La segunda etapa fue el estudio del tratamiento de la derivada en los programas de las asignaturas de las carreras de Ingeniería Comercial en Chile. Dicho estudio mostró que, si bien la mayor parte de las propuestas curriculares presentan similitudes en la organización de contenidos y en los elementos lingüísticos utilizados para la construcción del objeto derivada, se observan diferencias importantes en la preponderancia de la derivada interpretada como una razón de cambio y en los campos de problemas abordados (Galindo Illanes y Breda, 2022a, 2023a).

La tercera etapa fue el estudio de los significados pretendidos de la derivada en libros de texto para las carreas de Ingeniería Comercial en Chile, el cual evidenció: a) un énfasis en el significado parcial de la derivada como el límite del cociente de incrementos y un predominio del lenguaje simbólico en los argumentos; b) poca presencia de algunos teoremas importantes relacionados a la derivada y; c) falta de una representatividad de las definiciones de la derivada (Galindo Illanes y Breda, 2023b), pues no abarcaba la complejidad de este objeto matemático.

La cuarta etapa fue el diseño instruccional de un proceso de enseñanza y aprendizaje de la derivada para las futuras personas profesionales en ingeniería comercial, estudiantes de la carrera de Ingeniería Comercial de una universidad chilena (Galindo Illanes et al., 2023). Para la construcción del diseño instruccional, se tuvo en cuenta, además de las herramientas teóricas del Enfoque Ontosemiótico (explicadas en la secuencia del texto), los resultados de las etapas del estudio previamente mencionado.

Con base en lo anterior, este trabajo tiene como objetivo presentar los resultados de la implementación de un diseño instruccional de enseñanza de la derivada para las futuras personas profesionales en ingeniería comercial en Chile, estudiantes de la carrera de Ingeniería Comercial de una universidad chilena.

Marco teórico

Los desarrollos teóricos propuestos por el EOS, explicados en Godino et al. (2007) y reelaborados recientemente por Godino et al. (2019), tienen como objetivo dar respuesta a algunos problemas generados en el campo de la Educación Matemática.

En el EOS, se asume que la actividad matemática es una actividad humana centrada en la resolución de problemas, y acontece en un tiempo-espacio determinado, a través de una secuencia de prácticas. Para ello, el EOS propone las nociones de situación-problema y de práctica matemática que se realiza durante la resolución de estas situaciones-problema. Tales secuencias de prácticas tienen lugar en el tiempo y se suelen considerar, en muchos casos, como procesos. Cuando un sujeto lleva a cabo y evalúa una secuencia de prácticas matemáticas, activa un conglomerado formado por situaciones-problemas, lenguajes, definiciones, proposiciones, procedimientos y argumentos, articulados en lo que, en términos del EOS, se llama una configuración de objetos primarios Font et al. (2013).

Para explicar cómo emergen los objetos primarios, resulta útil la metáfora “subir una escalera”. Cuando se trepa una escalera siempre se debe apoyar en un pie, pero cada vez el otro pie está en un escalón superior. La práctica matemática se puede comparar con esta acción. El escalón en el que se busca apoyo para realizar la práctica usa una configuración de objetos primarios ya conocida, mientras que el escalón superior al que se accede, como resultado de la práctica realizada, puede generar nuevos objetos primarios que no eran conocidos antes.

En el EOS, Font et al. (2013) considera que el camino por donde los objetos matemáticos emergen a partir de las prácticas es complejo y deben ser distinguidos, al menos, dos niveles. En un primero, emergen los objetos primarios y después hay una segunda emergencia que es el resultado de diferentes factores que explican Font et al. (2013). Se trata de la emergencia de una referencia global asociada a diferentes configuraciones de objetos primarios, los cuales permiten realizar prácticas matemáticas en diferentes contextos; esto lleva a entender que ese objeto secundario se puede definir de diversas formas, representar de formas diferentes, etc. El resultado, según el EOS, es que exista un objeto, llamado en este artículo derivada, que juega el papel de referencia global de todas las configuraciones.

El EOS también asume el principio de que el conocimiento de un objeto, por parte de un sujeto (ya sea individuo o institución), es el conjunto de funciones semióticas que dicho sujeto puede establecer, en las cuales el objeto interviene como expresión o contenido. Además, la correspondencia entre un objeto y el sistema de prácticas donde tal objeto interviene se interpreta como el significado de ese objeto (institucional o personal).

Para delimitar los significados de un objeto matemático, el EOS propone la herramienta denominada análisis de sistemas de prácticas (personales e institucionales) y las configuraciones de objetos primarios involucradas en ellas (Godino, 2014; Godino y Batanero, 1994).

En Font et al. (2013) y Rondero y Font (2015) se explica que la noción de complejidad del objeto matemático secundario y la de articulación de los componentes de dicha complejidad tienen un papel esencial en la enseñanza y aprendizaje de dicho objeto. Entender la complejidad del objeto secundario, en términos de una pluralidad de significados, es resultado de la visión pragmatista sobre el significado que se asume en el EOS. Desde un punto de vista pragmatista, el significado de un objeto matemático (primario o secundario) se entiende como el conjunto de prácticas en la que dicho objeto interviene de una manera determinante (o no). Un objeto matemático, originado como un emergente del sistema de prácticas para resolver un campo de problemas específico, con el paso del tiempo queda enmarcado en diferentes programas de investigación. Cada nuevo programa permite resolver nuevos tipos de problemas, aplicar nuevos procedimientos, relacionar el objeto (y, por tanto, definir) de manera diferente, utilizar nuevas representaciones, entre otras funciones. De esta manera, con el paso del tiempo, aparecen nuevos subconjuntos de prácticas (sentidos) que amplían el significado del objeto secundario.

Ahora bien, para el objeto matemático secundario derivada, Pino-Fan et al. (2011) caracterizan su complejidad mediante nueve configuraciones de objetos primarios: 1) tangente en la matemática griega; 2) variación en la edad media; 3) métodos algebraicos para hallar tangentes; 4) concepciones cinemáticas para el trazado de tangentes; 5) ideas intuitivas de límite para el cálculo de máximos y mínimos; 6) métodos infinitesimales en el cálculo de tangentes; 7) cálculo de fluxiones; 8) cálculo de diferencias y 9) derivada como límite.

En Pino-Fan et al. (2013) se utilizan estas nueve configuraciones para la reconstruir el significado global de la derivada, el cual se utiliza para valorar la representatividad del significado pretendido en el currículo de Bachillerato de México. La caracterización de la complejidad de la derivada que proponen Pino-Fan et al. (2011) facilita tener elementos para diseñar cuestionarios que permiten caracterizar la comprensión del estudiantado, docentes en servicio sobre la derivada (Pino-Fan et al., 2015).

Al respecto, Galindo Illanes y Breda (2023b) profundizan el estudio de los significados de la derivada en el caso de que el objeto sea enseñado a estudiantes de Ingeniería Comercial. En este estudio, si se consideran las herramientas del EOS que se acaban de presentar y los estudios previos realizados (prerrequisitos para este) en Galindo Illanes et al. (2022, 2023) y Galindo Illanes y Breda (2022b, 2022a, 2023a, 2023b) se busca presentar los resultados de un proceso de instrucción de la derivada aplicado a futuras personas profesionales en Ingeniería Comercial en Chile.

Metodología

En este apartado se explica el contexto del estudio, los instrumentos de recolección de datos y el análisis de estos.

Contexto del estudio y participantes

En la investigación participaron 90 estudiantes de la carrera de Ingeniería Comercial de la Facultad de Economía y Negocio de una universidad chilena, con edades entre los 19 y 20 años. El plan de estudios de Ingeniería Comercial considera la asignatura de Cálculo Aplicado a los Negocios en el tercer semestre académico, y tiene como prerrequisito el curso de Álgebra o Métodos Cuantitativos.

Bases para una propuesta didáctica implementada

El plan de intervención implementado consideró, para el desarrollo de la enseñanza de la derivada, los siguientes aspectos:

a) Campos de problema. A partir del significado institucional pretendido y el análisis del significado de referencia de Galindo Illanes y Breda (2023b), la propuesta valoró los campos de problemas sobre: tangentes (CP1), el cálculo de derivadas a partir de reglas y teoremas de derivación (CP2), aplicaciones de la derivada para el cálculo de máximos y mínimos, y análisis de gráficas de funciones (CP3).

b) Configuraciones epistémicas. La propuesta tomó en cuenta las configuraciones epistémicas caracterizadas y utilizadas por Galindo, Breda y Alvarado (2023), estas son:

(i) Configuración manipulativa. Cada estudiante trabaja con papel, regla y lápiz. El lenguaje utilizado en esta configuración es característico de los procedimientos descriptivos y de la geometría analítica.

(ii) Configuración computacional. Cada estudiante cuenta con un dispositivo electrónico (notebook, celular o tableta), internet, GeoGebra (versión gratuita) y código QR. El lenguaje y los procedimientos son de tipo gráfico, geométrico y descriptivo.

(iii) Configuración algebraica. Cada estudiante tiene un dispositivo electrónico (notebook, celular o tableta), internet y software educativos como Symbolab (versión gratuita). El lenguaje y procedimientos son de tipo simbólico y tabular.

c) Trabajo presencial de aula y autónomo fuera de aula. La trayectoria didáctica consideró sesiones en aula y otras fuera del esta, todas dirigidas por la persona docente de la asignatura. Las sesiones de aula se desarrollaron en formato presencial y en los horarios establecidos de clases. Sin embargo, las sesiones fuera de aula no tuvieron horario establecido y se consideró el trabajo autónomo de cada estudiante.

Desarrollo de la enseñanza

El programa de actividad curricular de Cálculo Aplicado a los Negocios se llevó a cabo en 15 semanas, cada una dispuso de cuatro sesiones presenciales en aula, con una duración de 80 minutos por sesión. Además, semanalmente se dispuso de dos horas de trabajo autónomo, declaradas en el programa curricular de la asignatura.

Las sesiones presenciales de aula se realizaron en los horarios establecidos para las clases teóricas y prácticas, las actividades consideradas fueron individuales y grupales colaborativas, lo cual favorece el diálogo, la retroalimentación y la consolidación de los conocimientos adquiridos por cada estudiante durante su trabajo autónomo. Las sesiones fuera de aula se consideraron parte del trabajo autónomo e incluyeron actividades como visualizar videos educativos, leer apuntes teórico-prácticos y realizar las tareas disponibles en la plataforma virtual Moodle.

La secuencia de tareas implementadas correspondió al estudio de la derivada de funciones reales, a través de los campos de problemas CP1, CP2 y CP3. Para el desarrollo de la enseñanza se contemplaron cinco semanas de clases, la temporalización y la planificación se adaptaron del estudio de Galindo Illanes et al. (2023), se describen en la Tabla 1.

Tabla 1. Temporalización y planificación del estudio de los Campos de Problemas

Semana	CP	Sesiones Presenciales (SP)	Tiempo SP	Sesiones de trabajo autónomo (TA)	Tiempo TA
1	1	1-4	320 minutos	1	120 minutos
2	1	5-8	320 minutos	2	120 minutos
3	2	9-12	320 minutos	3	120 minutos
4	3	13-16	320 minutos	4	120 minutos
5	3	17-20	320 minutos	4	120 minutos

Nota: adaptación de Galindo Illanes et al. (2023).

La planificación del estudio de los campos de problemas de la derivada, contemplados en el programa de la asignatura, examinaron 20 sesiones presenciales de aula y ocho de trabajo autónomo fuera de esta, en un periodo de cinco semanas. En la Tabla 2 se presenta una adaptación de las actividades descritas en Galindo Illanes et al. (2023).

Tabla 2. Temporalización y planificación del estudio de CP1, CP2 y CP3

Sesión presencial (SP)	Campo de problemas (CP)	Acción didáctica	Objetivo de la acción didáctica	Lenguajes	Configuraciones
1-2	CP1	Tarea SP1	Obtener la pendiente de la recta tangente mediante aproximaciones por la pendiente de rectas secantes.	Tabular Geométrico Gráfico Descriptivo	Manipulativas Computacional
3-4	CP1	Tarea SP2	Identificación de la recta tangente a una curva.	Geométrico Gráfico Descriptivo	Manipulativas Computacional
5-6	CP1	Tarea SP3	Interpretación geométrica de la derivada en un punto particular (se utiliza una aproximación intuitiva a la noción de límite).	Simbólico Gráfica	Computacional Algebraica
7	CP1	Tarea SP4	Articulación de la derivada de una función en un punto y de la función “derivada” (consolidar utilizando la noción de derivada como límite de tasas medias de variación de la función).	Tabular Gráfica Simbólico Descriptivo	Computacionales Algebraica
8	CP1	Tarea SP5	Aplicación de la función “derivada” (utilizando la definición de límite).	Simbólico	Computacionales
9	CP2	Tarea SP6	Definición del álgebra de las derivadas: Si 𝑓 y g funciones reales no nulas y c ∈ ℝ – {0} , entonces: a) (𝑓 ± g)’ = (𝑓)’ ± (g)’ b) (c · 𝑓)’ = c ∙ (𝑓)’ c) (𝑓 ∙ g)’ = 𝑓’ ∙ g + 𝑓 ∙ g’ d)	Simbólico	Algebraica
10	CP2	Tarea SP7	Derivadas de las funciones: • 𝑓(x) = xn, ∀n ∈ ℝ, xn y x-n bien definida • 𝑓(x) = ex, ∀x ∈ ℝ, • 𝑓(x) = ln(x), ∀x > 0 (se mencionan en el programa como reglas de derivadas). Aplicación del álgebra de derivadas para calcular la derivada de otras funciones construidas mediante operaciones aritméticas entre la función “exponencial natural”, “logaritmo natural” y “polinomios”.	Simbólico Gráfico	Computacional Algebraica
11	CP2	Tarea SP8	Derivada de una función “compuesta” (regla de la cadena). Aplicación al cálculo de derivadas de otras funciones compuestas por funciones polinómicas, exponenciales y logarítmicas.	Simbólico Gráfico	Computacional Algebraica
12	CP2	Tarea SP9	Aplicación de las reglas de derivación y álgebra de las derivadas para el cálculo de costos marginales e ingresos marginales.	Simbólico	Algebraica
13	CP3	Tarea SP10	Articulación de la interpretación geométrica de la derivada y el criterio de la primera derivada para extremos relativos.	Gráfico Simbólico	Computacional
14	CP3	Tarea SP11	Aplicación del criterio de la primera derivada a problemas clásicos de optimización de funciones reales y económicas.	Gráfico Simbólico	Algebraica
15	CP3	Tarea SP12	Aplicación de la primera derivada al análisis de la monotonía de funciones reales y económicas, orientada al trazado de curvas.	Simbólico Gráfico	Computacional Algebraica
16	CP3	Tarea SP13	Aplicación del criterio de la segunda derivada a problemas clásicos de optimización de funciones reales y funciones económicas.	Gráfico Simbólico	Algebraica
17	CP3	Tarea SP14	Aplicación de la segunda derivada al análisis de la concavidad (hacia arriba y hacia abajo) de funciones reales y económicas, orientada al trazado de curvas.	Geométrico Gráfico	Computacional
18	CP3	Tarea SP15	Aplicación de la derivada a la optimización del costo en la construcción de una caja sin tapa.	Descriptivo	Manipulativa
19	CP3	Tarea SP16	Modelamiento de la función “costo” para la construcción de una caja sin tapa.	Geométrico Simbólico	Algebraica
20	CP3	Tarea SP17	Aplicación de la derivada a la optimización del costo en la construcción de una caja sin tapa.	Simbólico	Computacional Algebraica
1	CP1	Tarea TA1	Estudio del manuscrito teórico-práctico del curso, que considera la construcción de la ecuación de una recta tangente a una curva. Aplicación de la recta tangente a problemas económicos.	Simbólico Gráfica	Computacional Algebraica
2	CP1	Tarea TA2	Aplicación de la interpretación geométrica de la derivada.	Tabular Gráfica Simbólico Descriptivo	Computacionales Algebraica
3	CP2	Tarea TA3	Estudio del manuscrito teórico-práctico del curso, que considera el cálculo de derivadas utilizando el álgebra de derivadas.	Simbólico	Computacional Algebraica
4	CP2	Tarea TA4	Estudio del manuscrito teórico-práctico del curso, que considera el uso de las reglas de derivadas para el cálculo de funciones marginales.	Simbólico	Computacional Algebraica
5	CP3	Tarea TA5	Estudio del manuscrito teórico-práctico del curso, que considera la aplicación del criterio de la primera y segunda derivada a problemas clásicos de optimización de funciones reales y económicas.	Simbólico Gráfico	Computacional Algebraica
6	CP3	Tarea TA6	Estudio del manuscrito teórico-práctico del curso, que considera la aplicación de la primera derivada para el análisis de la monotonía de funciones reales y económicas.	Simbólico Gráfico	Computacional Algebraica
7	CP3	Tarea TA7	Estudio del manuscrito teórico-práctico del curso, que considera la aplicación de la segunda derivada para la optimización de funciones reales y económicas.	Simbólico Gráfica	Computacional Algebraica
8	CP3	Tarea TA8	Estudio del manuscrito teórico-práctico del curso, que considera la aplicación de los criterios de primera y segunda derivada para la optimización de funciones económicas.	Simbólico Gráfica	Computacional Algebraica

Nota: adaptación de Galindo Illanes et al. (2023).

Para comenzar el estudio de la derivada es fundamental construir previamente el concepto de la recta tangente a una curva, considerando las concepciones cartesiana y euclidiana (Galindo Illanes et al., 2022). Por esta razón durante las sesiones presenciales de 1 a 4 (tareas SP1 y SP2) y la sesión de trabajo autónomo 1 (tarea TA1) se le propuso al grupo de estudiantes resolver tareas para ampliar la concepción euclidiana (la tangente solo corta a la gráfica en un punto) a la cartesiana, mediante la construcción de la recta tangente como límite de rectas secantes (Galindo Illanes et al., 2023).

Además, con el objetivo de tematizar el esquema de recta tangente –es decir, que el esquema pueda ser considerado una totalidad coherente o, en términos del EOS, que el objeto resultante de la tematización sea un objeto situado en el segundo de los dos niveles de emergencia de los objetos considerados en el EOS. En otras palabras, se trata del surgimiento de una referencia global asociada a diferentes configuraciones cognitivas desarrolladas por el alumnado (Font et al., 2016), al considerar aplicaciones económicas y al relacionar el concepto de pendiente de la recta secante con el de costo medio y el de costo marginal como la aproximación de los costos medios calculados, destacando su equivalencia con la pendiente de la recta tangente (Galindo Illanes et al., 2022).

Con el propósito de relacionar la pendiente de la recta tangente a una curva con la derivada de la función en el punto de tangencia, las sesiones presenciales 5 y 6 (Tarea SP3) se enfocaron en identificar la tendencia de las pendientes de las rectas secantes con la derivada de la función en el punto de tangencia (Galindo Illanes et al., 2023). En la sesión 2 de trabajo autónomo (Tarea TA2) se consolidó la interpretación geométrica de la derivada, fortaleciendo el vínculo entre la pendiente de la recta tangente y la derivada en un punto.

Posteriormente, se articuló la derivada de una función en un punto y su función “derivada”, a través de la sesión presencial 7 (Tarea SP4), que promovió el tránsito entre las representaciones gráfica, tabular y analítica de 𝑓’, la expresión simbólica de la función 𝑓(x)era conocida y se construyó la función que cumplía con todas las pendientes de las rectas tangentes, esta correspondió a la expresión simbólica de 𝑓’ (x) (Font, 2005); entre las tareas desarrolladas se consideró el problema propuesto por Galindo y Breda (2023b). Luego se generalizó la función “derivada” como la que a cada valor le hace corresponder la pendiente de la recta tangente a la gráfica de 𝑓 en el punto (x, 𝑓(x)). Finalmente, a través de la manipulación de un applet de GeoGebra, se esperó que cada estudiante interpretara la función “derivada” n 𝑓’(x) como la función cuyas imágenes, y0 = 𝑓’(x0), correspondían a las pendientes de las rectas tangentes a la función 𝑓 en x0.

Las sesiones presenciales 8-9 (tarea SP5, SP6 y TA3) tenían el propósito de establecer la representación simbólica de la función “derivada” y el álgebra de esta. Para ello, se utilizó un lenguaje mayormente simbólico y la configuración algebraica.

Las sesiones presenciales de 10-12 (tarea SP7, SP8, SP9, TA3 y TA4) tenían como propósito establecer y aplicar las reglas de derivación. Si bien, al establecer las reglas de derivación, el lenguaje fue mayoritariamente simbólico, también se utilizó el gráfico, a través de un applet de GeoGebra que permitió visualizar de forma gráfica la función “derivada”. Además, se le propuso al estudiantado aplicar el álgebra de derivadas al cálculo de funciones marginales, utilizando configuraciones algebraicas y un lenguaje simbólico.

En las sesiones presenciales de la 13-15 (Tarea SP10, SP11, SP12, TA5 y TA6) se estableció una articulación entre la interpretación geométrica de la derivada y el criterio de la primera derivada, a través del análisis de la monotonía de una función “real”. Se utilizó un lenguaje en su mayoría gráfico y en menor medida simbólico. La configuración fue computacional gracias a la integración de un applet de GeoGebra. Finalmente, se estableció los criterios de la primera y segunda derivada para la resolución de problemas de optimización de funciones reales y económicas, además de aplicar la primera derivada al trazado de curvas de funciones reales y económicas.

Las sesiones presenciales 16-17 (Tarea SP13, SP14, TA7 y TA8) tuvieron como propósito aplicar el criterio de la segunda derivada a problemas clásicos de optimización de funciones reales y económicas. Su lenguaje fue gráfico y simbólico, y las configuraciones, algebraicas.

Finalmente, las sesiones de 18-20 tuvieron como propósito consolidar de manera manipulativa la aplicación de los criterios de primera y segunda derivada para optimizar una función “costo” (SP15, SP16, SP17). Se utilizó un lenguaje mayoritariamente gráfico y geométrico y, en menor medida, simbólico y descriptivo. La configuración fue computacional, manipulativa y algebraica.

Instrumentos de recolección de datos

Durante la implementación de las actividades y al finalizar cada campo de problemas se aplicó un instrumento evaluativo para realizar un análisis exploratorio del aprendizaje del estudiantado. A continuación, por motivos de espacio se presentan tres tareas, una para cada campo de problemas. Para la realización de estas tareas, cada estudiante dispone de notebook, internet, GeoGebra (versión gratuita) y Symbolab (versión gratuita). El lenguaje y los procedimientos son de tipo gráfico, descriptivo y simbólico, por lo que las configuraciones presentes corresponden al tipo computacional y algebraica.

La pregunta del campo de problemas 1 proporcionó información en torno al conocimiento del o la estudiante sobre tangentes, pues durante el desarrollo de las tareas deberían usar la configuración de recta tangente asociada al significado geométrico de la derivada en un punto para dar respuesta a las preguntas del enunciado (Figura 1).

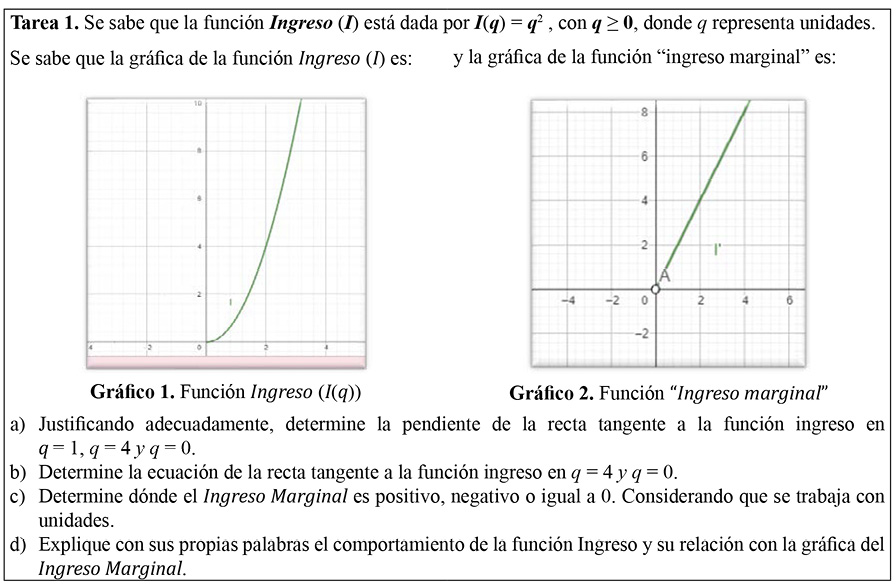
Figura 1. Tarea 1 aplicada a cada estudiante al finalizar el campo de problemas sobre tangente (CP1)

Nota: fuente Galindo Illanes et al., 2023.

En esta tarea se esperaba que cada estudiante: a) analizara el gráfico de la función “ingreso marginal” y estableciera que las pendientes de las rectas tangentes en q = 1, q = 4 y q = 0 son mq=1 = 2, mq=4 = 8, mq=0 = ∄. Además, darse cuenta de que la función “ingreso marginal” corresponde a la derivada de la función “ingreso”, por lo que su gráfico le provee la información necesaria para establecer las pendientes de las rectas tangentes. Se espera que b) pueda construir la ecuación de la recta tangente en q = 4, cada estudiante utilice mq=4 = 8 y del gráfico de la función “ingreso” obtenga I(4) = 16.

Con esta información, la ecuación de la recta tangente a la función “ingreso” es: I = 8q – 16. En c) cada estudiante debe analizar la gráfica de la función “ingreso marginal” y concluir que solo es positiva para q > 0 y no está definida para q ≤ 0. Finalmente, se debe mencionar la relación entre la monotonía de la función “ingreso” y su derivada; es decir, para q > 0 la función “ingreso marginal” es positiva y, en consecuencia, la función “ingreso” es creciente.

A continuación, la pregunta asociada al campo de problemas 2 proporcionó información en torno a la aplicación de las reglas de derivación en el cálculo de funciones marginales, utilizando configuraciones algebraicas y un lenguaje simbólico (Figura 2).

Figura 2. Tarea 2 aplicada al estudiantado al finalizar el campo de problemas sobre cálculo de derivadas a partir de reglas y teoremas de derivación (CP2)

Nota: elaboración propia de la investigación.

En esta tarea, se esperaba que cada estudiante aplicara el álgebra de las derivadas y derivadas de las funciones elementales (llamadas reglas de derivación) para el cálculo del costo marginal y del ingreso marginal, además debería indicarlas en orden a medida que fueron utilizadas. Por ejemplo: considerando ƒ yｇ funciones reales continuas, c y n una constante real, n ≠ –1.

Ingreso marginal

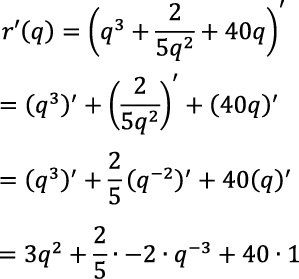
Álgebra de la derivada

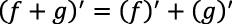
Álgebra de la derivada

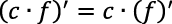
Regla de derivadas

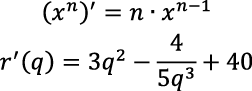
Luego, para determinar si es conveniente producir la unidad número 11. Se esperaba que cada estudiante evaluara las funciones marginales del ingreso y costo en q = 10, para poder predecir la conveniencia de la producción de la unidad número 11. En otras palabras,

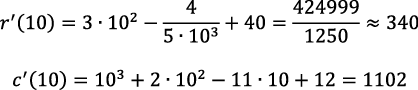
El estudiante debería concluir que, como c’ (10) > r’ (10), no es conveniente producir la unidad número 11.

Finalmente, se presenta una de las preguntas del instrumento que se aplicó al finalizar el campo de problemas 3. Esta pregunta permitió analizar la comprensión del estudiante en torno a la relación entre la representación gráfica de la función y de su derivada ƒ’, a través del criterio de la primera derivada para extremos relativos y el análisis de la monotonía (Figura 3).

Figura 3. Tarea 3 que se aplicó a los estudiantes al finalizar el estudio del campo de problemas aplicaciones de la derivada para el cálculo de máximos y mínimos, y análisis de gráficas de funciones (CP3)

Nota: elaboración propia de la investigación.

En este problema se espera que el estudiante modele la función “utilidad”, es decir:

U(q) = 0.004q3 + 4q2 + 430q – 5000, q ≥ 0

Luego se espera que derive la función “utilidad” y analice para cuáles valores reales de q:

U’ (q) = 0, U’ (q) > 0, U’ (q) < 0

Esto le permitió a cada estudiante determinar la monotonía de la función “utilidad” y, posteriormente, aplicar el criterio de la primera derivada para extremos relativos, con lo cual se obtiene el nivel de producción que maximiza la utilidad y la utilidad máxima. Al final, con la información de la monotonía de la función “utilidad” y los extremos relativos, cada estudiante pudo realizar un bosquejo de la gráfica de la función.

Método de análisis

Al finalizar la implementación, después de aplicar los instrumentos evaluativos, se realizó un análisis de tipo mixto (Johnson y Onwuegbuzie, 2004). Usando la noción de configuraciones de los objetos primarios del EOS, se cuantificó, para cada uno de los objetos primarios, la cantidad de acciones correctas (frecuencia) relacionadas con las resoluciones de los y las estudiantes en los problemas propuestos. Por su parte, desde el punto de vista cualitativo, fue posible identificar las respuestas y los argumentos correctos e incorrectos de cada estudiante al resolver las tareas planteadas.

Análisis y resultados

A continuación, se presentan algunos resultados obtenidos a partir del análisis de las respuestas del grupo de 90 estudiantes de Ingeniería Comercial. Además, se muestran evidencias (imágenes de respuestas) de los procedimientos y argumentos de algunas de las personas estudiantes.

La Tabla 3 explicita los resultados de la Tarea 1. Se observa que el 93 % de estudiantes identifica la relación entre la función “ingreso” y su marginal; por consiguiente, se puede inferir que comprenden que la función “ingreso marginal” proporciona las pendientes de las rectas tangentes. Además, se observa que el 78 % identifica las pendientes de las rectas tangente a la función “ingreso”, a partir de la función “ingreso marginal”. Finalmente, el 42 % del estudiantado, para el análisis de la monotonía de la función “ingreso”, justifica de forma correcta el vínculo entre la función “ingreso marginal” y la función “ingreso”.

Estos resultados indican una mejora en la construcción de la concepción cartesiana de la recta tangente, el aprendizaje de la relación entre la recta tangente a una curva con la interpretación geométrica de la derivada y la aplicación de la derivada en el análisis marginal, superando de esta forma algunas de las dificultades evidenciadas por las investigaciones previas (Biza y Zachariades, 2010; Galindo Illanes et al., 2022; Orts Muñoz et al., 2016; Santi, 2011).

Tabla 3. Frecuencia de aciertos de la Tarea 1 (n=90)

Acciones para los problemas sobre tangentes (CP1)	Objetos primarios	Frecuencia absoluta	Frecuencia relativa (%)
Justifica correctamente el vínculo entre la función “ingreso marginal” y la función “ingreso” para el cálculo de rectas tangentes.	Argumento	84	93
Relaciona correctamente la pendiente de la recta tangente a la curva con la derivada de la función en el punto de tangencia.	Definición	84	93
Identifica las pendientes de las rectas tangentes a la función “ingreso”.	Representación	70	78
Utiliza correctamente la fórmula de la ecuación de la recta punto-pendiente.	Procedimiento	65	72
Justifica correctamente el vínculo entre la función “ingreso marginal” y la función “ingreso” para el análisis de la monotonía de la función “ingreso”.	Argumento	38	42

Nota: elaboración propia de la investigación.

En la Figura 4 se observa que un estudiante identifica las pendientes de las rectas tangentes observando la función “ingreso marginal”; es decir, conoce el vínculo entre la función “ingreso” y su marginal. Además, construye correctamente las ecuaciones de las rectas tangentes a la función “ingreso”.

Figura 4. Desarrollo correcto de un estudiante en la construcción de la recta tangente a la función “ingreso”

Nota: elaboración propia de la investigación.

La Figura 5 muestra que, si bien el estudiante comprende que la gráfica de la función “derivada” le proporcionará las pendientes de las rectas tangentes, aún presenta algunas ambigüedades al momento de definirla, por lo cual manifiesta que “derivada es lo mismo que pendiente”. Se trata de una ambigüedad típica en este tema (derivada se puede referir tanto a la función “derivada” como a la derivada en un punto), que normalmente se desambigua por el contexto, ya que suele estar relacionada con el lenguaje utilizado por la persona docente al momento de explicar la definición de derivada. Por ejemplo, al utilizar expresiones metafóricas o un lenguaje simplificado para facilitar la comprensión del estudiantado (Löbner, 2013); o bien, puede estar relacionada con la dificultad de no poder manejar esta disparidad de significado que tiene el propio sujeto al momento de interpretar el término “derivada” (Godino et al., 2007).

Figura 5. Ambigüedad de un estudiante al referirse a la “derivada”

Nota: elaboración propia de la investigación.

La Figura 6 muestra que un estudiante encuentra la función algebraica que corresponde a la gráfica de la función “ingreso”, luego de eso obtiene su derivada, utilizando las reglas de derivación y construye las ecuaciones de las rectas tangentes solicitadas. Esto indica que el o la estudiante comprende que la derivada le proporcionará las pendientes de las rectas tangentes necesarias, sin embargo, no vincula la derivada del ingreso con su marginal.

Figura 6. Desarrollo algebraico de un estudiante en la construcción de la recta tangente a la función “ingreso”

Nota: elaboración propia de la investigación.

La Figura 7 muestra la justificación de un estudiante en torno al vínculo entre la función “ingreso marginal” y la función “ingreso”, para el análisis de la monotonía de la función “ingreso”. Sin embargo, se observa una imprecisión al definir el punto crítico.

Figura 7. Justificación de un estudiante sobre el comportamiento de la función “ingreso” y su relación con la gráfica del ingreso marginal

Nota: elaboración propia de la investigación.

La Tabla 4 presenta los resultados de la Tarea 2 que contestaron los y las estudiantes de Ingeniería Comercial. Se observa que el 97 % identifica y el 94 % aplica de manera correcta el álgebra de las derivadas. Además, el 89 % identifica y el 78 % aplica correctamente las reglas de las derivadas de las funciones elementales. Sin embargo, solo el 44 % aplicó correctamente la derivada en el análisis marginal y tomó la decisión correcta. De acuerdo con estos resultados, las actividades realizadas en el diseño instruccional le permitieron al estudiantado realizar correctamente el cálculo de derivadas a partir de reglas y teoremas de derivación. Sin embargo, se observan dificultades al aplicar la derivada para la toma de decisiones.

Tabla 4. Frecuencia de aciertos de la Tarea 2 (n=90)

Acciones para los problemas sobre cálculo de derivadas a partir de reglas y teoremas de derivación (CP2)	Objetos primarios	Frecuencia absoluta	Frecuencia relativa (%)
Indica correctamente el álgebra de las derivadas utilizadas para el cálculo de las funciones marginales.	Proposiciones	87	97
Aplica correctamente el álgebra de las derivadas en el cálculo de funciones marginales.	Procedimiento	85	94
Indica las reglas de derivación utilizadas para el cálculo de las funciones marginales.	Proposiciones	80	89
Aplica correctamente las reglas de derivación en el cálculo de funciones marginales.	Procedimiento	70	78
Evalúa el costo marginal en q = 10, para tomar una decisión en torno a la unidad número 11.	Procedimiento	40	44
Evalúa el ingreso marginal en q = 10, para tomar una decisión en torno a la unidad número 11.	Procedimiento	40	44
Justifica correctamente que es conveniente producir la unidad número 11.	Argumento	40	44

Nota: elaboración propia de la investigación.

La Figura 8 muestra la construcción de la función “costo marginal” que planteó una de las personas, indicando las reglas de las derivadas de las funciones elementales y álgebra de la derivada de manera correcta. Es decir, aplicó la derivada para obtener las funciones de costo e ingreso marginales.

Figura 8. Procedimiento de un(a) estudiante para obtener el costo marginal

Nota: elaboración propia de la investigación.

La Figura 9 muestra la interpretación correcta de la función “costo marginal” e “ingreso marginal”, al evaluarse en q = 10. Al estudiante se le solicita predecir para la unidad número 11, por lo que decide evaluar en la unidad 10; en otras palabras, el estudiante aplica la derivada en la función de “costo” e “ingreso marginal” y las interpreta correctamente.

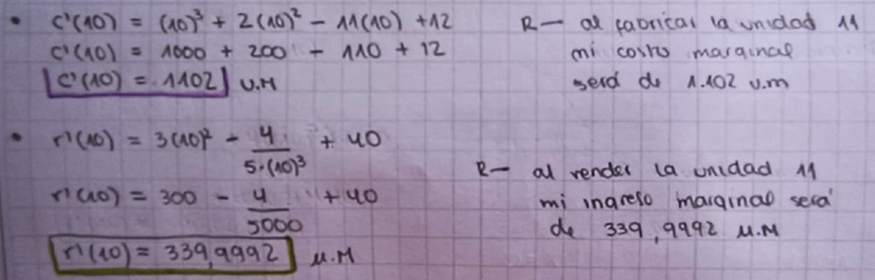
Figura 9. Interpretación de las funciones de “costo” e “ingreso marginal” al evaluar en q = 10

Nota: elaboración propia de la investigación.

Ahora bien, la Figura 10 expone la justificación correcta en la toma de decisión en torno a la producción de la unidad número 11, para ello cada estudiante utiliza el costo marginal e ingreso marginal evaluado en q = 10.

Figura 10. Justificación de no producir la unidad número 11

Nota: elaboración propia de la investigación.

La Tabla 5 presenta los resultados de la Tarea 3, se observa que el 98 % de la población estudiantil modela correctamente la función “utilidad” y determina su derivada al aplicar las reglas y teoremas de derivación; el 78 % identifica los valores críticos y el 76 %, los intervalos donde U’ (q) > 0 y U’ (q) < 0. Los errores observados son, en su mayoría, aritméticos y de álgebra básica; es decir, conocimientos previos. El 70 % aplica correctamente la derivada para el análisis de la monotonía de la función, sin embargo, solo el 56 % comprende que los valores críticos son posibles extremos y el 53 % que deben ser analizados utilizando el criterio de la primera derivada para extremos relativos. Finalmente, solo el 39 % de los y las estudiantes realizó el bosquejo de la gráfica de la función “utilidad”. Los resultados indican que, si bien el estudiantado aplica la derivada para el cálculo de máximos y mínimos, así como el análisis de gráficas de funciones, se observan limitaciones producto de la complejidad de los objetos matemáticos necesarios para construir la derivada, específicamente la función real, gráfico de funciones reales y ecuaciones.

Tabla 5. Frecuencia de aciertos de la Tarea 3 (n=90)

Acciones para los problemas sobre aplicaciones de la derivada para el cálculo de máximos y mínimos, y análisis de gráficas de funciones (CP3)	Objetos primarios	Frecuencia Absoluta	Frecuencia relativa
Modela correctamente la función “utilidad”.	Definición	88	98
Determina la derivada de la función “utilidad”, utilizando correctamente las reglas y álgebra de las derivadas.	Proposiciones	88	98
Determina correctamente los valores de q en el dominio, tal que U’ (q) = 0.	Procedimiento	70	78
Determina correctamente los valores de q en el dominio, tal que U’ (q) > 0.	Procedimiento	68	76
Determina correctamente los valores de q en el dominio, tal que U’ (q) < 0.	Procedimiento	68	76
Relaciona correctamente U’ (q) > 0 con el crecimiento de la función “utilidad”.	Proposiciones	63	70
Relaciona correctamenteU’ (q) > 0 con el decrecimiento de la función “utilidad”.	Proposiciones	63	70
Relaciona los valores de q tales que U’ (q) = 0 con los posibles extremos de la función “utilidad”.	Proposiciones	50	56
Aplica correctamente el criterio de la primera derivada para determinar el nivel de producción en el que se alcanza la utilidad máxima.	Proposiciones	48	53
Determina justificando correctamente la utilidad máxima.	Argumento	48	53
El bosquejo realizado describe correctamente la monotonía y extremos de la función “utilidad”.	Procedimiento	35	39

Nota: elaboración propia de la investigación.

La Figura 11 muestra la expresión simbólica correcta de la función “utilidad” y su derivada; es decir, el o la estudiante comprende que para optimizar la función “utilidad” requiere trabajar con su función “derivada”.

Figura 11. Función “utilidad” y su derivada construida correctamente por un(a) estudiante

Nota: elaboración propia de la investigación.

La Figura 12 muestra la obtención de los valores críticos al resolver la ecuación generada al igualar a cero la derivada de la función “utilidad”. En otras palabras, cada estudiante conoce la definición de puntos críticos y resuelve de forma correcta una ecuación de tercer grado utilizando algebra básica, se debe observar que la función “derivada” no presenta discontinuidades.

Figura 12. Obtención de los puntos críticos de la función “utilidad”

Nota: elaboración propia de la investigación.

La Figura 13 presenta la respuesta de un o una estudiante sobre la producción y venta de 1.000.000 para alcanzar la utilidad máxima; es decir, la persona aplica correctamente la derivada para optimizar las funciones económicas.

Figura 13. Justificación de la optimización de la función “utilidad”

Nota: elaboración propia de la investigación.

Conclusiones

El objetivo de este artículo fue presentar los resultados de la implementación de un diseño instruccional de enseñanza de la derivada para las futuras personas profesionales en ingeniería comercial en Chile. Dicho diseño pretendía presentar una cierta complejidad del objeto “derivada”, mediante el estudio de diversas configuraciones de objetos primarios: tangentes, aplicaciones de la derivada para el cálculo de máximos y mínimos, análisis de gráficas de funciones y el cálculo de derivadas a partir de reglas y teoremas de derivación. Además, se incorporó el uso de las TIC en las diversas tareas, lo cual favorece el tratamiento y la conversión entre los lenguajes escrito, numérico, gráfico y simbólico (Galindo Illanes et al., 2023; Galindo Illanes y Breda, 2023b).

Los resultados evidencian que el estudiantado participó de esa implementación, aunque presentaron algunas limitaciones, tales como la dificultad en el bosquejo de la función “utilidad” o la aplicación de la derivada para la tomada de decisiones; aprendieron la relación entre la tangente a una curva y la interpretación geométrica de la derivada y la aplicación de la derivada en el análisis marginal, lo cual mostró, además, una mejora en la construcción de la concepción cartesiana de la recta tangente.

Esos resultados están directamente relacionados con los aspectos innovadores de esta investigación. El primer aspecto fue la utilización transversal, en toda la unidad didáctica, de recursos TIC (applets, GeoGebra, códigos QR). El segundo corresponde al tiempo dedicado, en la programación, a la interpretación geométrica de la derivada, pues fue esa noción la que le permitió al grupo de estudiantes resolver una mayor diversidad de problemas presentes en la carrera de Ingeniería Comercial, tales como los de optimización.

Además, a partir de la interpretación geométrica de la derivada las personas participantes elaboraron de forma global la construcción del concepto de la derivada. El tercero aspecto se refiere a los problemas de aplicación. En esta investigación se ha trabajado, por ejemplo, gráfica de funciones y optimización de funciones vinculadas al contexto de economía y negocios. Dicho en términos de los criterios de idoneidad didácticos, el diseño puso el énfasis en el criterio epistémico, el mediacional y el ecológico, y los resultados de la implementación muestran que se consiguió, en un grado razonable, el criterio cognitivo, contrario a los criterios que el profesorado de matemáticas de facultades de ingeniería en Perú utiliza (Garcés et al. 2021; 2022).

En particular, los estudiantes han construido un significado de la derivada con diferentes significados parciales bien conectados, lo cual les permite una cierta competencia para resolver tareas relacionadas con su profesión.

Una de las limitaciones del estudio fue el tiempo insuficiente destinado al desarrollo de las tareas, dado que las personas participantes no tenían todos los conocimientos previos necesarios para comprender los nuevos conceptos. Por ejemplo, para que el o la estudiante pudiera realizar una tarea sobre la interpretación geométrica de la derivada, fue necesario destinar tiempo para retomar conocimientos sobre funciones. Otra limitación se ha dado por las fallas de conexión con la red de internet, lo cual dificulta la accesibilidad del alumnado al material, ya que debían conectar sus móviles a los códigos QR para accederlos.

Como perspectiva futura, esta investigación muestra que, para una mejor formación de ingenieros e ingenieras comerciales, entendida en términos de que sean competentes en la aplicación de las derivadas a problemas relacionados con su profesión, se hace necesario un cambio en los programas de las asignaturas que incluyen la enseñanza de la derivada; a fin de que contemplen explícitamente una más completa y significativa variabilidad de campos de problema, incorporando la complejidad de la derivada. En particular, su interpretación geométrica, dado que es la noción más utilizada en la Ingeniería Comercial.

En particular la implementación realizada muestra que es posible implementar este tipo de enseñanza de la derivada. Además, se hace necesario un proceso de formación del cuerpo docente encargado de formar a las futuras personas profesionales en esta área , habilitándolos en la enseñanza de los diferentes significados de la derivada, sus distintos campos de problemas, representaciones, procedimientos, argumentos, proposiciones y aplicaciones contextuales junto a los recursos TIC.

Financiamiento

Vicerrectoría de Investigación y Doctorado de la Universidad San Sebastián (USS-FIN-23-DOCI-04); PID2021-127104NB-I00 (MICIU/AEI/10.13039/501100011033) y por “FEDER Una manera de hacer Europa.

Consentimiento informado

Las personas autoras declaran documentar el consentimiento informado firmado por las personas participantes del estudio.

Conflicto de intereses

Las personas autoras declaran no tener algún conflicto de interés.

Declaración de la contribución de las personas autoras

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo. El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: M. K. G. I. 50 % y A. B. 50 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por la persona autora correspondiente M. K. G. I. y A. B., previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://doi.org/10.1590/SciELOPreprints.6650

Referencias

Ariza Cobos, Á. y Linares Ciscar, S. (2009). Sobre la aplicación y uso del concepto de derivada en el estudio de conceptos económicos en estudiantes de Bachillerato y Universidad. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 27(1), 127-136. https://doi.org/10.5565/rev/ensciencias.3667

Ballard, C. L. y Johnson, M. F. (2004). Basic math skills and performance in an introductory economics class. The Journal of Economic Education, 35(1), 3-23. https://doi.org/10.3200/JECE.35.1.3-23

Biza, I. y Zachariades, T. (2010). First year mathematics undergraduates’ settled images of tangent line. The Journal of Mathematical Behavior, 29(4), 218-229. https://doi.org/10.1016/j.jmathb.2010.11.001

Butler, J. S., Finegan, T. A. y Siegfried, J. J. (1994). Does more calculus improve student learning in intermediate micro and macro-economic theory? The American Economic Review, 84(2), 206-210. https://www.jstor.org/stable/2117830

Font, V. (2005). Una aproximación ontosemiótica a la didáctica de la derivada. En A. Maz, B. Gómez y M. Torralbo (Eds.), Noveno Simposio de la Sociedad Española de Educación Matemática SEIEM (pp. 111-128). Sociedad Española de Investigación en Educación Matemática (SEIEM).

Font, V., Godino, J. D. y Gallardo, J. (2013). The emergence of objects from mathematical practices. Educational Studies in Mathematics, 82(1), 97-124. https://doi.org/10.1007/s10649-012-9411-0

Font, V., Trigueros, M., Badillo, E. y Rubio, N. (2016). Mathematical objects through the lens of two different theoretical perspectives: APOS and OSA. Educational Studies in Mathematics, 91, 107-122. https://doi.org/10.1007/s10649-015-9639-6

Galindo Illanes, M. K. Breda, A. (2022a). El tratamiento de la derivada en el plan de estudios de Ingeniería Comercial en Chile. En T. F. Blanco, C. Núñez-García, M. C. Cañadas y J. A. González-Calero (Eds.), Investigación en Educación Matemática XXV (pp. 285-293). SEIEM.

Galindo Illanes, M. K. y Breda, A. (2022b). Estudo da derivada com o uso das TIC realizado com estudantes de engenharia no Chile. En C. A. Hauschild Johann y S. Nunes Lopes (Eds.), Docência e ciência: [re]valorização do conhecimento (1.a ed., Vol. 1, pp. 110-117). Editora Univates.

Galindo Illanes, M. K. y Breda, A. (2023a). A derivada no plano de estudos dos cursos de Engenharia Comercial no Chile. En A. L. Manrique y C. L. O. Groenwald (Eds.), Anais do IX Congresso Iberoamericano de Educação Matemática (pp. 2173-2183). Editora Akadem.

Galindo Illanes, M. K. y Breda, A. (2023b). Significados de la derivada en los libros de texto de las carreras de Ingeniería Comercial en Chile. Bolema: Boletim de Educação Matemática, 37(75), 271-295. https://doi.org/10.1590/1980-4415v37n75a13

Galindo Illanes, M. K., Breda, A. y Alvarado Martinez, H. (2023). Diseño de un proceso de enseñanza de la derivada para estudiantes de Ingeniería Comercial en Chile. PARADIGMA, 44(4), 321-350. https://doi.org/10.37618/PARADIGMA.1011-2251.2023.p321-350.id1386

Galindo Illanes, M. K., Breda, A., Manríquez, D. D. C. y Martínez, H. A. A. (2022). Analysis of a teaching learning process of the derivative with the use of ICT oriented to engineering students in Chile. EURASIA Journal of Mathematics, Science and Technology Education, 18(7), em2130. https://doi.org/10.29333/ejmste/12162

Garcés, W. y Font, V. (2022). Criterios que guían la práctica del profesor de matemáticas en cursos de ciencias básicas para ingeniería. Uniciencia, 36(1), 66-81. https://doi.org/10.15359/ru.36-1.5

Garcés, W., Font, V. y Morales-Maure, L. M. (2021). Criteria that guide the Professor’s practice to explain mathematics at basic sciences courses in engineering degrees in Peru. A case study. Acta Scientiae, 23(3), 1-33. https://doi.org/10.17648/acta.scientiae.6389

García, L., Azcárate, C. y Moreno, M. (2006). Creencias, concepciones y conocimiento profesional de profesores que enseñan cálculo diferencial a estudiantes de ciencias económicas. Revista latinoamericana de investigación en matemática educativa, 9(1), 85-116. https://www.scielo.org.mx/scielo.php?pid=S1665-24362006000100005&script=sci_arttext

Godino, J. D. (2014). Síntesis del enfoque ontosemiótico del conocimiento y la instrucción matemática: motivación, supuestos y herramientas teóricas. En Universidad de Granada (pp. 1-60). http://www.ugr.es/local/jgodino/eos/sintesis_EOS_24agosto14.pdf

Godino, J. D. y Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en didactique des Mathématiques, 14(3), 325-355.

Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM - International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1

Godino, J. D., Batanero, C. y Font, V. (2019). The onto-semiotic approach: Implications for the prescriptive character of didactics. For the Learning of Mathematics, 39(1), 37-42. https://www.jstor.org/stable/26742011

Hey, J. D. (2005). I teach economics, not algebra and calculus. The Journal of Economic Education, 36(3), 292-304. https://doi.org/https://doi.org/10.3200/JECE.36.3.292-304

Johnson, R. B. y Onwuegbuzie, A. J. (2004). Mixed methods research: A research paradigm whose time has come. Educational researcher, 33(7), 14-26. https://doi.org/https://doi.org/10.3102/0013189X033007014

Larios, V. y Jiménez, A. (2022). Significados parciales de la derivada en libros universitarios en la formación de ingenieros. Praxis & Saber, 13(33), e12274-e12274. https://doi.org/10.19053/22160159.v13.n33.2022.12274

Larios, V., Murillo, R. E. P. y Reyes, H. M. (2021). Significados sobre la derivada evidenciados por alumnos de carreras de Ingeniería en una universidad mexicana. Avances de Investigación en Educación Matemática, 20(20), 105-124. https://doi.org/10.35763/AIEM20.4002

Löbner, S. (2013). Understanding semantics. Routledge. https://doi.org/10.4324/9780203528334

Orts Muñoz, A., Llinares Ciscar, S. y Boigues Planes, F. J. (2016). Elementos para una Descomposición Genética del concepto de recta tangente. Avances de investigación en educación matemática, 10, 111-134. https://doi.org/10.35763/aiem.v0i10.164

Pino-Fan, L. R., Castro, W. F., Godino, J. D. y Font, V. (2013). Idoneidad epistémica del significado de la derivada en el currículo de bachillerato. Paradigma, 34(2), 129-150. http://ve.scielo.org/scielo.php?pid=S1011-22512013000200008&script=sci_arttext

Pino-Fan, L. R., Godino, D. J. y Font, V. (2015). Una propuesta para el análisis de las prácticas matemáticas de futuros profesores sobre derivadas. Bolema: Boletim de Educação Matemática, 29(51), 60-89. https://doi.org/10.1590/1980-4415v29n51a04

Pino-Fan, L. R., Godino, J. D. y Font, V. (2011). Faceta Epistémica Del Conocimiento Didáctico-Matemático sobre la Derivada. Educ. Matem. Pesq., 13, 141-178. http://funes.uniandes.edu.co/24491/1/Pino-Fan2011Faceta.pdf

Pino-Fan, L. R., Godino, J. D. y Font, V. (2016). Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: the case of the derivative. Journal of Mathematics Teacher Education, 21(1), 63-94. https://doi.org/10.1007/S10857-016-9349-8

Rodríguez-Nieto, C., Rodríguez-Vásquez, F. y Font, V. (2022). Nueva mirada para analizar las conexiones desde dos lentes teóricos: la teoría ampliada de las conexiones matemáticas y el enfoque ontosemiótico. En J. G. Lugo-Armenta, L. R. Pino-Fan, M. Pochulu y W. F. Castro (Eds.), Enfoque Onto-Semiótico del Conocimiento y la Instrucción Matemáticos: investigaciones y desarrollos en América Latina (1.a ed., Vol. 1, pp. 193-219). Universidad de Lagos.

Rondero, C. y Font, V. (2015). Articulation of the mathematical complexity of the arithmetic mean. Enseñanza de las Ciencias, 33(2), 29-49. https://doi.org/10.5565/rev/ensciencias.1386

Santi, G. (2011). Objectification and semiotic function. Educational Studies in Mathematics, 77(2), 285-311. https://doi.org/10.1007/S10649-010-9296-8

---