
Revista UNICIENCIA
Uniciencia Vol. 38(1), January-December, 2024
E-ISSN: 2215-3470
DOI: https://dx.doi.org/10.15359/ru.38-1.15
Mathematical Modeling and Threshold Analysis of Acceptable Failure Rate and Academic Standard
Modelado matemático y análisis de umbral de tasa de reprobación aceptable y estándar académico
Modelagem matemática e análise de limite de taxa de reprovação aceitável e padrão acadêmico
Abayomi Ayotunde Ayoade1*, Mojisola Manuel2, Motunrayo Ajoke Adeosun3
Received: Aug/15/2023 • Accepted: Mar/15/2024 • Published: Jul/31/2024
|
Abstract A certificate is evidence of participating in a process, and anyone who holds a certificate is believed to have the prerequisites necessary to handle what the certificate qualifies them for. However, this perception might be incorrect if the certificate has been obtained by taking shortcuts. [Objective] In this paper, a compartmental model was developed to quantify factors that could put the authenticity of a certificate in doubt by examining the trade-off between academic standards and failure rates in the context of tertiary education institutions in Nigeria. [Methodology] The model was validated using several mathematical theorems. Equilibria for the model and the threshold for acceptable academic performance were derived. Stability analysis was carried out by using the stability theory of differential equations based on the derived acceptable academic performance threshold. [Results] The theoretical results for the model were validated through numerical simulations, and the results from the simulations linked acceptable failure rates to academic performance falling below the threshold of the institutions’ standards. [Conclusions] The policy implication of the result is that an increase in the supply of qualified graduates into Nigeria’s labor markets, as well as a reduction in the rate of unemployment, is a function of maintaining academic standards. Keywords: certificate; compartmental model; academic standard; failure rates; tertiary education institutions. Resumen El certificado es una evidencia de participación en un proceso y se cree que cualquier persona que posea uno tiene un requisito previo para manejar todo aquello para lo que este califica. Sin embargo, la impresión podría fallar, si el certificado se hubiera obtenido tomando atajos. [Objetivo] En este documento se desarrolló un modelo compartimental para cuantificar los factores que podrían poner en duda la autenticidad de un certificado, mediante el examen de la compensación entre el estándar académico y las tasas de reprobación, en el contexto de las instituciones de educación terciaria en Nigeria. [Metodología] El modelo se demostró válido utilizando algunos amplios teoremas matemáticos. Se derivaron los equilibrios para dicho método y el umbral para un rendimiento académico aceptable. El análisis de estabilidad se llevó a cabo empleando la teoría de la estabilidad de ecuaciones diferenciales, basada en el umbral de rendimiento académico aceptable obtenido. [Resultados] Los resultados teóricos del modelo fueron validados por medio de simulaciones numéricas y los de las simulaciones vincularon la tasa de reprobación aceptable con el rendimiento académico que cayó por debajo del umbral del estándar establecido por las instituciones. [Conclusiones] La implicación política del resultado es que el aumento en la oferta de graduados calificados en los mercados laborales de Nigeria, así como la reducción en la tasa de desempleo, son una función del mantenimiento de los estándares académicos. Palabras clave: certificado; modelo compartimentado; estándar académico; tasas de reprobación; instituciones de educación terciaria. Resumo O certificado é uma prova de participação em um processo e acredita-se que quem o possui tem como pré-requisito realizar tudo para o qual o referido certificado o qualifica. No entanto, a impressão poderia falhar se o certificado tivesse sido obtido através de atalhos. [Objetivo] Neste artigo, foi desenvolvido um modelo compartimental para quantificar fatores que poderiam pôr em dúvida a autenticidade de um certificado, examinando o compromisso entre o padrão académico e as taxas de reprovação no contexto de instituições terciárias referenciadas na Nigéria. [Metodologia] O modelo foi provado válido usando alguns teoremas matemáticos amplos. Os equilíbrios para o modelo e o limite para desempenho acadêmico aceitável foram derivados. A análise de estabilidade foi realizada utilizando a teoria da estabilidade de equações diferenciais com base no limite de desempenho acadêmico aceitável derivado. [Resultados] Os resultados teóricos do modelo foram validados por meio de simulações numéricas e os resultados das simulações relacionaram a taxa de reprovação aceitável com o desempenho acadêmico que ficou abaixo do limite do padrão estabelecido pelas instituições. [Conclusões] A implicação política do resultado é que o aumento da oferta de licenciados qualificados nos mercados de trabalho nigerianos, bem como a redução da taxa de desemprego, é uma função da manutenção dos padrões académicos. Palavra-chave: certificado; modelo compartimental; padrão acadêmico; taxas de reprovação; instituições terciárias. |
The objective of education in Nigeria is the preparation and training of young individuals for future challenges and workforce requirements of the nation (Ayoade & Farayola, 2020a). In acknowledging the essence of education in individuals’ development in particular and the society in general, the government of Nigeria outlined how education can facilitate the required transformation in the country in the National Policy on Education in 1977, 1981, 1998 (revised in 2004) (Federal Republic of Nigeria, 2004). Based on the document, tertiary institutions are saddled with the responsibility of turning out graduates who would be able to solve problems of the society and foster all-round development.
A tertiary institution means any institution that provides post-school education on a full-time, part-time, or distance basis (Razu et al., 2018). It refers to a university or other tertiary education providers recognized by employers that offer degrees, diplomas, or teacher education courses (Yusuf et al., 2020). Tertiary education is a third-level education that is pursued after secondary education, and individuals seeking admission into tertiary institutions must pass certain examinations to be qualified (Thompson et al., 2020).
Unfortunately, admission processes into tertiary institutions are threatened by examination malpractice which has been a major problem confronting the educational system in Nigeria. It has been widely discussed and is being considered a main challenge not only to the examination bodies but also to the entire educational system, the school administrators, the government, and the society at large (Akunne, 2021; Adegbite, 2019; Okey & Ewa, 2019).
Generally, many candidates who secure admission into tertiary institutions in Nigeria today indulge in examination malpractice (Osadebe & Bini, 2018; Kawugana & Wayopwa, 2017). These sets of individuals may not have the background knowledge to cope with academic demands in higher institutions. Although, some of them may be influenced by the seriousness of few students who got admissions into the institutions on merit as well as the available education facilities in the school to turn over a new leaf. Also, it is possible for some of the students who are admitted on merits to succumb to bad influence, become unserious and join the group of students who intend to succeed by cutting corners.
The essence of a grade in academic reports is to convey the academic performance of the students (Ayoade & Agboola, 2022a). Besides, success or the extent to which a student meets the standards set by the government and the institution are measured by academic performance. Furthermore, academic performance determines the extent to which the teachers and school leaders are successful in terms of pedagogical and management practices (Razu et al., 2018). Based on the cardinal impact of the academic performance of students on teachers’ and school administrators’ achievements, they are constrained to uphold standards and do face the temptation of lowering academic standards to protect their integrity and to remain relevant in the system.
Teachers and school administrators may be tempted to adjust scores to make the failure rate negligible. However, tertiary institutions may fail in their mandate of producing graduates who can rule their world and solve the problems of society if academic standards are compromised. The case of Nigeria is worrisome considering the high level of unemployment in the country, which has been blamed on the compromise of academic standards (Adelowokan et al., 2019; Aminu, 2019; Ayoade et al., 2020b). The rates of unemployment for Nigeria in 2018 and 2022 were 22.6 % and 40 % respectively (Ayoade et al., 2020c; Utomi, 2022).
Given the context above, it is imperative to examine the middle ground between the failure rates and academic standards at the tertiary level of education in Nigeria, which the present study attempts to address via a modeling approach. As far as we know, both the subject and the approach employed to conduct the analysis are completely new in the literature. Till now, no work has explored mathematical modeling of a compartmental kind to analyze the trade-off between failure rates and academic standards.
Examination malpractice is a major challenge to the education system in Nigeria. Apparently, a good number of students who are admitted into Nigeria’s tertiary institutions are products of examination malpractice (Ayoade & Farayola, 2020a; Ayoade & Agboola, 2022a). Based on this, a compartmental model CMSE is designed to analyze the trade-off between failure rates and academic standards in the context of tertiary institutions in Nigeria. The model is split into C(t), M(t), S(t), and E(t), respectively, where C(t) is the class for students who got admission into the institution through cheating, M(t) is the class for those who got admission through merits, S(t) is the class for those students who have what it takes to withstand the institution set standard, while E(t) denotes the class of individuals who graduated from the institutions on merit. The movement across compartments of the model is illustrated in Figure 1.
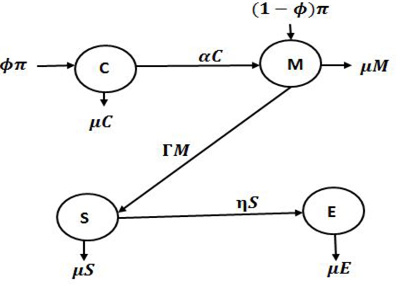
Figure 1. Transfer diagram of the model
Note: derived from research.
In Figure 1, students are admitted into the institutions at rates 𝜙𝜋 and (1 – 𝜙)𝜋. While 𝜙𝜋 is the rate of admitting students who indulge in cheating, (1 – 𝜙)𝜋 is the rate of admitting students who stand on merit. Students who got admission through cheating but who become serious about getting to the institution and do everything academically possible to meet the academic challenges move to compartment M(t) at a rate 𝛼. 𝜂 is the rate at which students graduate from the institutions on merits. Γ is the tendency of meeting up with the institutions’ set standards and is quantified as∈ ϑ where ∈ is the rate at which students who are serious cope with the institutions’ set standards and ϑ denotes the level of their seriousness. If the per capita probability of success for unserious students in the examination is 𝜏, then the effective rate of maintaining academic standard Γ𝜑 = ∈ ϑ (1 – 𝜏) S. Students in M(t), either those who are recruited to it directly from the society or those who move to it from C(t), may relax. Parameter 𝜏 is checking the level of academic standards and the quality of graduates that are being produced. An increase in 𝜏 will mean a fall in academic standards and vice-versa.
The study is based on the assumptions that students who got admission through cheating C(t) and those who are admitted by merit M(t), as well as those who can cope with the academic standards of the institution S(t) leave their respective compartments when they drop out at the same rate 𝜇. Individuals who get admission through cheating may drop out if they cannot cope or for other reasons. Those who are admitted on merits, and every other individual who has what it takes to withstand the institutions’ academic standards, may also drop out if they secure scholarships or through other reasons. Also, it is assumed that the rate of dropout is the same as the rate at which qualified graduates leave their compartment E(t) when they secure employment.
Based on the aforestated assumptions, formulations, and the transfer diagram, the following first-order ODEs are derived:
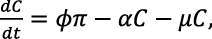 (1)
(1)
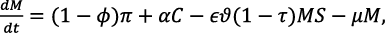 (2)
(2)
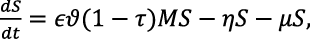 (3)
(3)
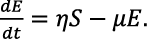 (4)
(4)
The model governs the connection between academic standards and failure rates in tertiary institutions in Nigeria. It can be employed to establish the trade-off between the two variables and to guide teachers and school administrators in determining an acceptable failure rate. The nomenclature for the parameters is stated in Table 1 for quick reference.
Table 1. Model’s parameters and nomenclature
|
Parameters |
Interpretations |
|
𝜋 |
Recruitment rate into the institutions |
|
∈ |
Rate of coping with the institutions’ set standard by the students |
|
ϑ |
Level of seriousness of the students |
|
𝜏 |
Rate of examination success for unserious students |
|
𝜙 |
Probability of being admitted into the institution through cheating |
|
𝜂 |
Rate of graduating qualified students |
|
𝛼 |
Rate at which students who got admission through cheating turn over a new leaf in the institution |
Note: derived from research.
The model is suitable to conduct the study if its solutions exist and are unique, positive, and, at the same time, mathematically well-posed (i.e., bounded). Each of these features shall be examined one after the other.
Existence and Uniqueness of Solutions
Theorem 1. The solutions for the model exist and, at the same time, are unique if the partial derivative of each state variable with respect to time in each equation is strictly less than infinity, i.e., 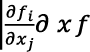 .
.
Proof. The proof for Theorem 1 is contained in many modeling studies (Ayoade et al., 2020b; Ayoade et al., 2020c; Adenuga et al., 2021). By inspection, the model satisfies the condition 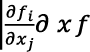 ; therefore, the model has solutions and the solutions are unique.
; therefore, the model has solutions and the solutions are unique.
Positivity of Solutions
Theorem 2. The solution for each state variable of the model remains positive for all t ≥ 0.
Proof. The model characterized a real-life phenomenon (i.e., education); hence it is reasonable to argue that each state variable admits only nonnegative initial conditions for all t ≥ 0. It is, therefore, straightforward to use differential equation theory to show that each state variable also admits only positive solutions for all t ≥ 0 as in (Ayoade et al., 2020b; Adenuga et al., 2021).
Boundedness of Solutions
Theorem 3. The solutions for the model remain feasible and bounded within the close
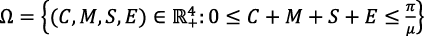 .
.
Proof. The model adds up to 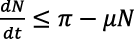 from which
from which 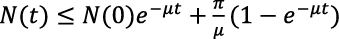 can be derived following the standard comparison theorem (Lakshmikantham et al., 1994). As
can be derived following the standard comparison theorem (Lakshmikantham et al., 1994). As 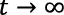 ,
, 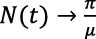 and all the solutions for the model enter the positive octant Ω which is not only positively invariant but positively attracting. Hence, the model is mathematically well posed and for the starting point x ∈ Ω, the path of x is contained in Ω. Therefore, the analysis of the model is sufficient to be considered on Ω where the solutions for the model are bounded.
and all the solutions for the model enter the positive octant Ω which is not only positively invariant but positively attracting. Hence, the model is mathematically well posed and for the starting point x ∈ Ω, the path of x is contained in Ω. Therefore, the analysis of the model is sufficient to be considered on Ω where the solutions for the model are bounded.
We shall analyze the model qualitatively and quantitatively to examine the trade-off between failure rate and academic standard in Nigeria’s tertiary institutions. Two possibilities can be considered. It is possible that the mechanism that is put in place to prevent students who got admission through cheating from progressing achieve complete success. Under that condition, compartment C(t) becomes zero with time, and nobody progresses from C(t) to M(t). On the other hand, there is a possibility for the mechanism to be ineffective so that all the compartments are non-empty. The former situation relates to disease-free equilibrium (DFE) while the latter relates to endemic equilibrium (EE) in epidemic modeling (Ayoade & Ibrahim, 2022b; Ayoade et al., 2023a; Ayoade et al., 2023b; Adeyemo & Ayoade, 2023).
However, since the model quantified the disease in the education system and not in human populations, the former situation shall be denoted rising standard equilibrium (RSE) and the latter, falling standard equilibrium (FSE). Suppose the rising standard equilibrium (RSE) is represented by Po = (Co, Mo, So, Eo) then Po can be derived as in Adenuga et al. (2021) if compartment C and the right-hand side of the system are zero. The result for Po , based on the condition, is given in equation (5) as
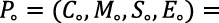
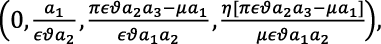 (5)
(5)
where a1 = (𝜇 + 𝜂), a2 = (1 – 𝜏), a3 = (1 – 𝜙).
If the falling standard equilibrium (FSE) is also denoted by P* = (C*, M*, S*, E*)then P* can be derived as in Ayoade & Farayola (2022c) if the RHS of the model is reduced to zero and the reduced system is solved simultaneously on the condition that each variable is non-zero. The coordinates of P* are given as follows:
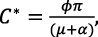 (6)
(6)
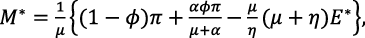 (7)
(7)
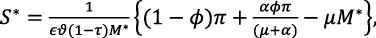 (8)
(8)
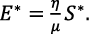 (9)
(9)
Academic Standard and Failure Rate Trade-off Ratio Rs
The concept of reproduction number Ro in epidemic modeling, which has been extensively discussed in the literature, is employed to analyze the trade-off between academic standards and failure rates in this work (see, for example, Favor & Anya, 2020; Sulayman et al., 2021; Khan et al., 2020; and the literature therein). Teachers and school administrators believe that their performance depends on the academic performance of their students. However, quality output in terms of rising academic standards must not be sacrificed for quantity output in terms of reduction in academic standards in the interest of the society. Hence, teachers and school administrators need to strike a balance between academic standards and failure rates to save their mandate and protect the interest of the society. The quantity Rs is, therefore, a threshold for acceptable academic performance. The two compartments M(t) and S(t) shall be adopted to derive parameter Rs as in disease modeling where compartments for infections are employed. Compartments M(t) and S(t) are considered in deriving Rs because the assessment of students that determine academic standards, and also academic standards that govern the quality of graduates that are being produced, depends on them (i.e., M(t) and S(t)). Following the Next Generational Matrix Operator as in Adenuga et al. (2021), the parameter Rs is derived as
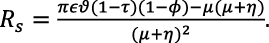 (10)
(10)
The step-by-step method used by Adenuga et al. (2021) to derive RG is employed to derive Rs in the present study. Unlike in disease modeling but following the same approach as in Adenuga et al. (2021) and Ayoade & Farayola (2021), academic standards are maintained, and the institution is producing individuals that are worth their certificates if Rs > 1. On the other hand, individuals whose performance falls below Rs (i.e., Rs > 1) do not meet the standards of the institution and deserve to fail. The failure rate becomes acceptable when Rs < 1. Having derived the threshold for acceptable academic performance, the stability of equilibria shall be examined.
Two equilibria—rising standard equilibrium (RSE) and falling standard equilibrium (FSE)— have been discussed so far, but the stability of only rising standard equilibrium shall be analyzed because only rising academic standard is of interest to the policymakers and the society. While RSE characterizes occasions when academic standards are being maintained, FSE considers situations when academic standards are relaxed. The popular linearization method shall be employed to investigate the local stability of the model around Ro. Linearizing the model around Ro as in Favor & Anya (2020), Adenuga et al. (2021), and Khan et al. (2020), we derive
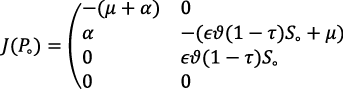
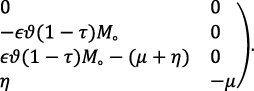 (11)
(11)
Theorem 4. The rising standard equilibrium of the model is locally asymptotically stable if Rs > 1 but unstable if Rs < 1.
Proof. The existence of local stability for the model around Ro depends on the signs of the eigenvalues of equation (11) or the signs of the trace and determinant of the matrix J (Po) J (Po) . The rising standard equilibrium is stable locally if all the eigenvalues of J (Po) in equation (11) are negative or if the trace of the matrix J (Po) is less than zero when the determinant of J (Po) is greater than zero.
The matrix J (Po) comprises the eigenvalues λ1 = – (μ + α) and λ2 = – μ as well as submatrix A given as
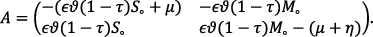 (12)
(12)
Substituting the values of Mo and So from equation (5) in equation (12) and simplifying, the trace of matrix A is given as
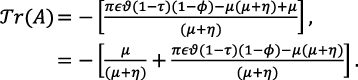 (13)
(13)
In view of equation (10),
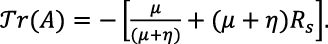 (14)
(14)
Since Rs is a non-negative quantity, then 𝒯r (A) < 0 .
Also,
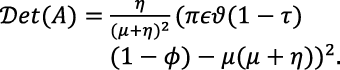 (15)
(15)
𝒟et (A) is already positive irrespective of the sign of πϵϑ (1 – τ)(1 – ϕ) – μ (μ + η). Hence, the rising standard equilibrium of the model is locally asymptotically stable since the conditions 𝒯r (A) < 0 and 𝒟et (A) > 0 are satisfied.
The implication of the rising standard equilibrium of the model being locally asymptotically stable is that academic standards are maintained, and a particular tertiary institution in Nigeria is fulfilling its mandate of producing graduates who can impact their environments.
Global Stability of Rising Standard Equilibrium Po
The comparison theorem outlined in Adenuga et al. (2021) shall be employed to examine the global stability of the model around Po.
Theorem 5. The rising standard equilibrium of the model is globally asymptotically stable if all the eigenvalues of the generational matrix (F – V) are negative.
Proof. The condition Rs > 1 guarantees the negativity of all the eigenvalues of the generational matrix (F – V).
The generational matrices F and V, following Adenuga et al. (2021), are defined as
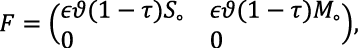 (16)
(16)
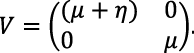 (17)
(17)
Therefore, |(F – V) – λ| = 0 evaluated around Rs produces
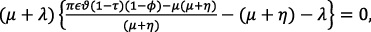 (18)
(18)
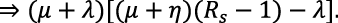 (19)
(19)
Therefore,
λm = – μ and λm = – (μ + η)(Rs – 1).
λm is already negative. λn is negative if and only if Rs > 1 and the rising standard equilibrium of the model is globally asymptotically stable; otherwise, it is unstable. The reason why λn is negative only ifRs > 1 and not if Rs < 1 has been expounded in recent articles (Adenuga et al., 2021; Ayoade & Farayola, 2021; Ayoade & Agboola, 2022a; Ayoade & Farayola, 2022c).
This ends the proof.
The implication of the rising standard equilibrium of the model being globally asymptotically stable is that academic standards are not compromised in all tertiary institutions in Nigeria, and the institutions are fulfilling their mandates.
Mathematical modeling came in to solve the challenges of missing data during analysis; we have plenty of data sources, empirical data, estimated data, data from related literature, or experts’ opinion data. In the present study, it is difficult to use a particular tertiary institution in Nigeria as a case study for fear of being held for incrimination. Therefore, the use of primary data is not feasible. Also, data from related literature or experts’ opinion data are not obtainable because the study is entirely new. However, hypothetical data (as in Ayoade et al., 2019; Ayoade & Farayola, 2020a; Ayoade & Farayola, 2021;) shall be adopted to carry out numerical simulation for the study.
Assuming a memo was received by the Head of the Department of Mathematics of a university in Nigeria from the management of the institution, revealing the high failure rates of the students across courses with large classes in a particular academic session, where the Department of Mathematics recorded the highest number of courses with high failure rates as follows:
Table 2. Students’ performance analysis across courses with large classes in an academic session
|
S/N |
Course Codes |
Failure Rates |
Students Total |
|
1 |
MTH 231 |
31 % |
315 |
|
2 |
MTH 233 |
29 % |
535 |
|
3 |
MTH 222 |
28 % |
337 |
|
4 |
MTH 223 |
25 % |
452 |
|
5 |
MTH 221 |
26 % |
294 |
|
6 |
STA 222 |
30 % |
300 |
|
7 |
STA 211 |
24 % |
264 |
Note: derived from research.
Suppose the management directed the HOD to inform the lecturers who had taught the above courses that there was mass failure and it was unacceptable. Suppose the management also argued further that the high failure rate was a result of improper teaching and warned the lecturers who had taught the courses to improve their teachings in order to forestall future occurrences of such mass failure. In this memo, many questions are begging for answers: Is there mass failure in the first instance, or is the failure rate too high? If there is, are the lecturers the cause of it or the ones to be blamed, given the mode of entry of many students into the institution in terms of widespread examination malpractice in the country and the nonchalant attitude of many students to study? Our model can provide answers to these and many more questions. The threshold for acceptable academic performance (Rs) derived in equation (10) can inform the policymakers whether the failure rate in Table 2 is acceptable or unacceptable in the interest of the society. We shall evaluate Rs using hypothetical values for all the parameters except the rate of examination success for unserious students 𝜏, which will take the values of each failure rate one by one in Table 2. Refer to Table 1 for the nomenclature of each parameter. The results of the evaluation are in Table 3.
Table 3. Stability of academic standards with failure rates as in the memo
|
Course codes |
𝜋 |
∈ |
ϑ |
𝜏 |
𝜙 |
𝜂 |
𝜇 |
Rs |
Remark |
|
MTH 231 |
0.55 |
0.75 |
0.8 |
0.31 |
0.01 |
0.3 |
0.1 |
1.1589 |
Stable |
|
MTH 233 |
0.55 |
0.75 |
0.8 |
0.29 |
0.01 |
0.3 |
0.1 |
1.1997 |
Stable |
|
MTH 222 |
0.55 |
0.75 |
0.8 |
0.28 |
0.01 |
0.3 |
0.1 |
1.2202 |
Stable |
|
MTH 223 |
0.55 |
0.75 |
0.8 |
0.25 |
0.01 |
0.3 |
0.1 |
1.2814 |
Stable |
|
MTH 221 |
0.55 |
0.75 |
0.8 |
0.26 |
0.01 |
0.3 |
0.1 |
1.2610 |
Stable |
Note: derived from research.
If examination integrity is not relaxed in tertiary institutions, only those who have what it takes to do well would be seeking admission into the institution (𝜋), academic standards would be high, and the rate of coping with the standards for unserious students would be high as well (∈). Rates of seriousness for the students would also be high (ϑ), and the chance of entry into the institution through examination malpractice would be low (𝜙). Lastly, the rate of producing qualified graduates would be high (𝜂). In Table 3, the aforesaid conditions are met, and the failure rate (𝜏) takes the values of the memo in Table 2. It is observed that the academic standard and failure rate trade-off ratio (Rs) is greater than one at all points. The equilibrium of the model is stable locally and globally since Rs > 1. Therefore, the failure rates for all the courses can be described as acceptable. The failure rates were OK because those who failed did not meet the minimum standard (i.e., Rs > 1). Based on the analysis, teachers and school administrators should be bold enough to stand by the result in Table 2 in the interest of the society. The effect on the society is the increase in the number of qualified graduates that are being produced which can be visualized in Figure 2 (see blue curve).
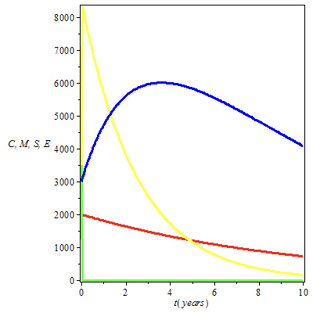
Figure 2. Dynamics of academic standard and failure rate when Rs > 1
Note: derived from research.
Figure 2 is plotted by using parameters space in Table 3 with C(t), M(t), S(t), and E(t) depicted with red, green, yellow, and blue colors, respectively. Particularly, the parameters space for MTH 222, together with C (t) = 2000, M (t) = 5000, S (t) = 3500, E (t) = 3000 and 𝛼 = 0.001 are used to generate the plot. It is observed from Figure 2 that when the academic standard is not compromised, there is a significant increase in the number of qualified graduates E(t) that are being produced by the institution in the first five years. This is the region where the equilibrium of the model is stable (i.e., Rs > 1). The failure rate in the memo (see Table 2) is acceptable, given the rising trend in the population of qualified graduates in Figure 2. If the results in Table 2 were to be tampered so that the failure rate was reduced, the society would be the one to suffer the consequences of the incompetent students that were allowed to graduate. Besides, the failure rate in Table 2 cannot be blamed on lecturers alone, as conveyed in the memo. What about students’ academic past performance? What about the work done at home? What about the students’ personal behavior towards studies? All these are factors to be considered for students’ poor performance. Tertiary institutions are designed for mature students. There are facilities and also handbooks that clearly outline the contents of the courses to be taught. Students can make use of the handbook for preparation before the classes and even after the classes. So, serious students can still meet the standard and pass examinations with little assistance from the lecturers.
On the other hand, if the concern of the university management in the memo is taken care of, that is, if the scoring system is adjusted so that the failure rate in Table 2 is reduced, some parameters would be affected (e.g., 𝜋, ∈, ϑ, 𝜙, and 𝜂). Admission seekers would increase since it is easy to pass (𝜋); the standard would be relaxed, making coping for unserious students easier as well (∈); the level of seriousness for students would fall (ϑ); and the likelihood of securing admission via cheating would also be high 𝜙. Finally, the quality of graduates being produced would drop (𝜂). Assuming the failure rates for the courses are reduced by three and a half (3.5) in Table 2 so that the values of the aforementioned parameters are also changed accordingly, then the effect on the academic standard and failure rate ratio (Rs) are shown in Table 4.
Table 4. Stability of academic standards with adjustment in the failure rates in the memo
|
Course codes |
𝜋 |
∈ |
ϑ |
𝜏 |
𝜙 |
𝜂 |
𝜇 |
Rs |
Remark |
|
MTH 231 |
0.25 |
0.4 |
0.3 |
0.089 |
0.03 |
0.1 |
0.1 |
0.1628 |
Unstable |
|
MTH 233 |
0.25 |
0.4 |
0.3 |
0.083 |
0.03 |
0.1 |
0.1 |
0.1671 |
Unstable |
|
MTH 222 |
0.25 |
0.4 |
0.3 |
0.08 |
0.03 |
0.1 |
0.1 |
0.1693 |
Unstable |
|
MTH 223 |
0.25 |
0.4 |
0.3 |
0.071 |
0.03 |
0.1 |
0.1 |
0.1758 |
Unstable |
|
MTH 221 |
0.25 |
0.4 |
0.3 |
0.074 |
0.03 |
0.1 |
0.1 |
0.1737 |
Unstable |
|
STA 222 |
0.25 |
0.4 |
0.3 |
0.086 |
0.03 |
0.1 |
0.1 |
0.1649 |
Unstable |
|
STA 211 |
0.25 |
0.4 |
0.3 |
0.069 |
0.03 |
0.1 |
0.1 |
0.1773 |
Unstable |
Note: derived from research
In Table 4, 𝜏 is determined by dividing the value of each 𝜏 in Table 3 by 3.5. Other parameters also varied from Table 3 accordingly. We are of the opinion that if the failure rate 𝜏 is reduced by 3.5, so that the failure rate for all the courses is less than 10%, as indicated by 𝜏 in Table 4; then the university management might be pleased and satisfied with the results since the management did not specify an acceptable failure rate in the memo. However, the effect of the exercise is inimical to productivity, as shown in Table 4. The academic standard and failure rate trade-off ratio (Rs) is below unity at all points, meaning that the equilibrium of the model is unstable in all the regions. Therefore, the rate of failure, though low, is unacceptable in the interest of the society. The reason, based on Table 4, is that it is achieved when the level of seriousness for students (ϑ) and the coping rate for unserious students (∈) are below average. The direct effect on society is the reduction in the number of qualified graduates that are being produced (𝜂), which can be visualized in Figure 3 (see blue curve).
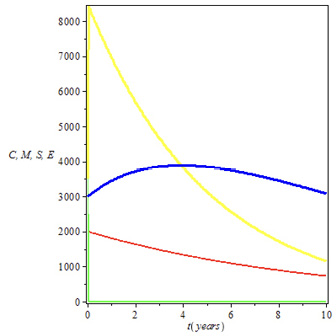
Figure 3. Dynamics of academic standard and failure rate when Rs < 1
Note: derived from research.
Figure 3 is generated by using parameters space for MTH 222 in Table 4, together with C (t) = 2000, M (t) = 5000, S (t) = 3500, E (t) = 3000 and 𝛼 = 0.001. From Figure 3, it is shown that there is no significant increase in the population of qualified graduates that are being produced over time compared to Figure 2. Figure 3 corresponds to the falling parts of Figure 2, and it is instigated by the compromise of academic standards. Based on the results of the analysis, the failure rates in the memo in Table 2 cannot be said to be too high, and the lecturers should not be coerced to adjust the scores in the interest of the society; rather, the students who failed should be supported through counseling to attain academic excellence.
In this paper, the trade-off between academic standards and failure rates in tertiary institutions in Nigeria has been theoretically investigated via a mathematical modeling method. A compartmental model has been formulated and the model has been proved valid using some ample mathematical theorems. The equilibria, as well as the threshold for acceptable academic performance, have been derived for the model. The stability of rising academic standard equilibrium has also been examined based on the threshold for acceptable academic performance. The theoretical results of the model have been validated by numerical simulations, and the results of the simulations showed that the increase in the supply of qualified graduates in Nigeria’s labor markets is a function of uncompromising academic standards. Since a certificate is evidence of participating in a process, and tertiary institutions are set up to produce individuals that would be able to impact their environments and foster all-round development, we, therefore, recommend that the failure rates, no matter their levels, should not be deemed unacceptable in Nigeria’s tertiary institutions inasmuch as those who failed did not meet the set standards for the country to overcome its numerous challenges.
Throughout the work, both theoretical and numerical approaches have been employed to gain insight into prevailing educational phenomenon in Nigeria; and for simplicity, hypothetical data from a single department in one college on very few Mathematics and Statistics courses have been used to generalize for the whole country. It is hoped that future studies will take care of the limitations in the present analysis. Future studies will attempt to adopt estimated data from many colleges and focus more on courses apart from Mathematics and Statistics.
The authors declare no competing interests.
Both authors declare that the final version of the paper was read and approved. The total percentage contribution for the conceptualization, preparation, validation, reviewing and editing of this article was as follows: A.A.A. 50 % , M.M. 25 % and M.A.A. 25 %.
Data sharing is not applicable since no new data was created or analyzed in this study.
A Preprint version of this paper was deposited in: https://ir.unilag.edu.ng/handle/123456789/12524
Adegbite, P. I. (2019). Examination malpractice as a malady to the development of educational programs in Nigeria. International Journal of Environmental Studies and Safety Research, 4(3), 49-53.
Adelowokan, O. A., Maku, O. E., Babasanya, A. O., & Adesoye, A. B. (2019). Unemployment, poverty and economic growth in Nigeria. Journal of Economics and Management, 35(1), 4-11.
Adenuga, J. I., Ajide, K. B., Odeleye, A. T., & Ayoade, A. A. (2021). Abundant natural
resources, ethnic diversity and inclusive growth in sub-Saharan Africa: a mathematical approach. Application and Applied Mathematics, 16(2), 1221-1247.
Akunne, L. I., Chigbo-Obasi, T. U., & Iwogbe, E. C. (2021). Perceived strategies for curbing examination malpractice among secondary school students in Nigeria. Asian Journal of Education and Social Studies, 20(4), 8-17.
Aminu, A. (2019). Characterizing graduate unemployment in Nigeria as education-job mismatch problem. African J. of Economics Review, 7(2), 113-130.
Ayoade, A. A., Farayola, P. I., & Lamidi, T. O. (2019). Dynamics and stability analysis of party switching in politics of Nigeria: a mathematical approach.Daffoldil International University Journal of Science and Technology,14(1), 53-60.
Ayoade, A. A., & Farayola, P. I. (2020a). Dynamics of examination malpractice among the key players in Nigeria. Daffodil International University Journal of Science and Technology, 15(2), 28-32.
Ayoade A. A., Folaranmi R., & Latunde T. (2020b). Mathematical analysis of the implication of the proposed rise in the retirement age on the unemployment situation in Nigeria. Athens Journal of Sciences, 7(1), 29-42. https://doi.org/10.30958/ajs.7-1-3
Ayoade, A. A, Odetunde, O., & Falodun B. (2020c). Modeling and analysis of the impact of vocational education on the unemployment rate in Nigeria. Application and Applied Mathematics: An International Journal (AAM). 15(1), 550-564.
Ayoade, A .A., & Farayola, P. I. (2021). A mathematical modelling of economic restoration through agricultural revitalisation in Nigeria. Journal of Quality Measurement and Analysis, 17(1), 79-91.
Ayoade, A. A., & Agboola, S. O. (2022a). Mathematical analysis of the causes of examination malpractices in Nigeria: an epidemic modelling approach, Journal of Science and Mathematics Letters, 10(1), 44-54. https://doi.org/10.37134/jsml.vol10.1.5.2022
Ayoade, A.A., & Ibrahim, M.O. (2022b). Analysis of transformation dynamics and mitigation of COVID-19 in Nigeria: an insight from a mathematical model. The Aligarh Bulletin of Mathematics, 41(1), 81-106.
Ayoade, A. A. & Farayola, P. I. (2022c). A mathematical model to address out-of-school children menace for actualisation of sustainable development in Nigeria. Journal of Science and Arts, 22(3), 677-692. https://doi.org/10.46939/J.Sci.Arts-22.3-a14
Ayoade, A. A., Nkuba, N. & Ibrahim, M. O. (2023a). An epidemic model for control and possible elimination of Lassa fever. Tamkang Journal of Mathematics, DOI: 10.5556/j.tkjm.55.2024.503
Ayoade, A. A., Oyedepo, T., & Agunbiade, S. (2023b). Mathematical modeling of Toxoplasma gondii between the environment and cat population under vaccination and sanitation. Journal of Fractional Calculus and Applications (JFCA). 14(1), 75-87.
Adeyemo, A. A., & Ayoade, A. A. (2023). Mathematical modeling of the effect of vaccination on the dynamics of infectious diseases. Nepal Journal of Mathematical Sciences (NJMS), 4(1), 1-10. https://doi.org/10.3126/njmathsci.v4i1.53151
Favour, A. O., & Anya, O. A. (2020). Mathematical model for Lassa fever transmission and control. Mathematics and Computer Science, 5(6), 110-118.
Federal Republic of Nigeria (2004). National policy on education, Revised edition, Lagos.
Kawugana, A., & Wayopwa, A. K. (2017). Impact of examination malpractice on the quality of graduates in Nigeria. International Journal of Education and Evaluation, 3(6), 45-51.
Khan, M.A., Atangana, A., & Alzahrani, E. (2020). The dynamics of COVID-19 with quarantine and isolation. Advances in Difference Equations, 2020(1), 1-22.
Lakshmikantham, V., Leela, S., & Kaul, S. (1994). Comparison principle for impulsive differential equations with variable times and stability theory. Nonlinear Analysis, Theory, Methods & Application, 22(4), 499-503.
Okey, A. S., & Ewa, A. M. (2019). Examination malpractice and corruption among students at Cross River State University of Technology, Calabar, Nigeria. International Journal of Quantitative and Qualitative Research Method, 7(2), 27-38.
Osadebe, P. U., & Bini, M. F. (2018). Assessment of factors affecting examination malpractice. European Journal of Educational Studies, 4(1), 20-33.
Razu, S. R., Akter, S., & Afrin, S. (2018). Factors affecting academic performance in tertiary education: a case study from Khulna University of Bangladesh. Pabna University of Science and Technology Studies, 3(1), 88-91.
Sulayman, F., Abdullah, F. A., & Mohd, M. H. (2021). An SVEIRE model of tuberculosis to assess the effect of an imperfect vaccine and other exogenous factors. Mathematics, 9,327. https://doi.org/10.3390/math9040327
Thompson, J. D., Ansoglenan, G., & Laar, S. (2020). Why do students engage in examination malpractice? The University for Development Studies experience. Journal of Social Science Studies, 7(1), 8-26.
Utomi, J.M. (24 March, 2022). Unemployment and a nation’s 40 per cent of hopelessness. The Guardian-Nigeria. https://guardian.ng/opinion/unemployment-and-a-nations-40-per-cent-of-hopelessness/
Yusuf, F. A., Okanlawon, A. E., & Oladayo, T. R. (2020). Investigation into factors affecting students’ academic performance in tertiary institutions as expressed by undergraduates. Journal of Education in Black Sea Region, 5(2), 62-75.
1* Corresponding author
Abayomi Ayotunde Ayoade,
 ayoadeabbayomi@gmail.com,
ayoadeabbayomi@gmail.com,  https://orcid.org/0000-0003-3470-0147
https://orcid.org/0000-0003-3470-0147Mojisola Manuel,
 drmojimanuel@gmail.com,
drmojimanuel@gmail.com,  https://orcid.org/0000-0003-3062-7464
https://orcid.org/0000-0003-3062-7464Motunrayo Ajoke Adeosun,
 mogunfowora@unilag.edu.ng,
mogunfowora@unilag.edu.ng,  https://orcid.org/0000-0001-7037-0363
https://orcid.org/0000-0001-7037-0363Department of Mathematics, Faculty of Science, University of Lagos, Lagos, Nigeria.
2 Department of Arts and Social Sciences Education, University of Lagos, Lagos, Nigeria.
3 Department of Adult Education, University of Lagos, Lagos, Nigeria.
Mathematical Modeling and Threshold Analysis of Acceptable Failure Rate and Academic Standard (Abayomi Ayotunde Ayoade • Mojisola Manuel • Motunrayo Ajoke Adeosun) Uniciencia is protected by Attribution-NonCommercial-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0)
URL: www.revistas.una.ac.cr/uniciencia
Correo electrónico: revistauniciencia@una.cr


