Competencia docente del profesorado de educación primaria en el área de medidas en un contexto de reforma curricular

Teaching competence of primary school teachers in the area of measurement in a context of curricular reform

Competência docente dos professores do ensino fundamental em medidas de áreas num contexto de reforma curricular

Marianela Alpízar-Vargas1*, Ceneida Fernández2, Salvador Llinares2

Received: Aug/16/2023 • Accepted: Feb/1/2024 • Published: Aug/31/2024

Resumen [Objetivo] El objetivo es explorar cómo las personas docentes en activo miran profesionalmente los materiales curriculares y el pensamiento matemático del estudiantado en el área de medida. [Metodología] Las personas participantes fueron 18 docentes en estado activo de educación primaria. Resolvieron un cuestionario formado por 12 ítems con tres focos: (i) interpretar el pensamiento matemático del alumnado, (ii) proponer actividades para apoyar la comprensión del estudiantado y (iii) analizar actividades relacionadas con las referencias del currículo, sobre magnitudes y sus medidas. El análisis se llevó a cabo en dos etapas. En la primera, se identificaron características de la manera en la que el personal docente respondía a cada uno de los ítems y, en la segunda, se agruparon las características según los tres focos para identificar particularidades sobre cómo el grupo docente interpreta el pensamiento matemático del estudiantado y proponían actividades, y cómo analizaban estas usando el currículo [Resultados] Los resultados indican que las personas docentes presentan dificultades para identificar errores por no considerar el contexto real del problema. Además, aunque fueron capaces de proponer diferentes actividades, tuvieron conflictos cuando se les solicitaba que la actividad se ubicara en un contexto cotidiano. La diferenciación curricular entre habilidad y proceso matemático se mostró difícil para el profesorado en el área de la medida. [Conclusiones] Las limitaciones presentadas por el profesorado muestran la necesidad de que se desarrollen propuestas de formación continua para docentes de educación primaria en activo donde se fomente el desarrollo competencias docentes. Palabras clave: docentes en activo; educación primaria; mirar profesionalmente; pensamiento matemático del estudiantado; materiales curriculares. Abstract [Objective] The aim is to explore how in-service teachers professionally view curricular materials and students’ mathematical thinking in the area of measurement. [Methodology] The participants were 18 in-service primary school teachers, who completed a 12-item questionnaire with three focuses: (i) interpret students’ mathematical thinking, (ii) propose activities to support students’ understanding, and (iii) analyze activities related to curriculum references regarding magnitudes and their measurements. The analysis was conducted in two stages. In the first stage, the characteristics of the responses by in-service teachers to each of the items were identified, and in the second stage those characteristics were grouped according to the three focuses in order to identify any peculiarities on how teachers interpreted students’ mathematical thinking and proposed and analyzed activities using the curriculum. [Results] Results indicate that teachers have difficulties in identifying errors because they do not consider the real context of the problem. Furthermore, although they were able to propose different activities, they had difficulties when asked to place the activity into an everyday context. The curricular difference between mathematical process and ability proved to be difficult for teachers in the area of measurement. [Conclusions] Teachers’ limitations show the need to develop continuing education proposals for in-service primary teachers that foster the development of teaching competences. Keywords: in-service teachers; primary education; view professionally; student mathematical thinking; curriculum materials Resumo [Objetivo] O objetivo é explorar como professores ativos veem profissionalmente os materiais curriculares e o pensamento matemático dos alunos em medidas de áreas. [Metodologia] Participaram 18 professores ativos do ensino fundamental. Eles resolveram um questionário composto por 12 itens com três focos: (i) interpretar o pensamento matemático dos alunos, (ii) propor atividades para apoiar a compreensão dos alunos e (iii) analisar atividades relacionadas às referências curriculares, magnitudes e suas medidas. A análise foi realizada em duas etapas. Na primeira foram identificadas características da forma como o corpo docente respondia a cada um dos itens e, na segunda, as características foram agrupadas de acordo com os três focos para identificar particularidades sobre como o grupo docente interpreta o pensamento matemático dos alunos e propunham atividades, e como as analisavam usando o currículo. [Resultados] Os resultados indicam que os professores têm dificuldades em identificar erros porque não consideram o contexto real do problema. Além disso, embora conseguissem propor atividades diferentes, tiveram conflitos quando lhes foi pedido que situassem a atividade num contexto quotidiano. A diferenciação curricular entre habilidade e processo matemático mostrou-se difícil para os professores de medidas de áreas. [Conclusões] As limitações apresentadas pelos professores mostram a necessidade de desenvolver propostas de formação continuada para professores ativos do ensino básico onde o desenvolvimento de competências docentes seja incentivado. Palavras-chave: professores ativos; Educação primária; olhar profissionalmente; pensamento matemático dos alunos; materiais curriculares.

Introducción

La noción de competencia docente se define como la capacidad de emplear el conocimiento de matemáticas y de didáctica de las matemáticas en las tareas que integran la práctica de enseñanza matemática; tales como analizar y diseñar actividades adecuadas, interpretar el pensamiento matemático del alumnado o gestionar las interacciones matemáticas en el aula (Fernández et al., 2018; Llinares y Fernández, 2021). Desde esta perspectiva, la competencia docente “mirar profesionalmente” se articula a través de los focos que centran la atención del profesorado: las producciones matemáticas de las personas alumnas, los materiales y recursos curriculares, o la gestión del discurso matemático en el aula (Fernández et al., 2018).

La competencia “mirar profesionalmente” ha recibido una gran atención durante los últimos años (e. g. Dindyal et al., 2021; Weyers et al., 2023). La mayoría de estos estudios ha aportado información sobre cómo las personas docentes en formación inicial “miran profesionalmente” el pensamiento matemático del estudiantado para decidir la forma de continuar la instrucción en diferentes dominios matemáticos (e. g. Callejo et al., 2022; Fernández et al., 2018; Fisher et al., 2019; van den Kieboom et al., 2017). Además, los estudios previos también han aportado contextos favorables para su desarrollo en los programas de formación inicial o continua; por ejemplo, el uso de representaciones de la práctica (Fernández et al., 2018), el empleo de lentes teóricas como trayectorias hipotéticas de aprendizaje (Fernández y Choy, 2020; Ivars et al., 2020) o las discusiones en línea o la retroalimentación recibida de parte de una persona tutora (Fernández et al., 2020).

Sin embargo, estos estudios también han subrayado las dificultades del profesorado en decidir sobre la instrucción, considerando la comprensión previa de las personas estudiantes (Barnhart y van Es, 2015; Ivars et al., 2020; Tyminski et al., 2020). Teniendo en cuenta las dificultades del cuerpo docente en la toma de decisiones, se genera la necesidad de indagar cómo el profesorado “mira profesionalmente” los materiales curriculares (libros de texto, materiales de internet, entre otros), los cuales tienen a su disposición para tomar decisiones sobre la enseñanza.

Así, el caracterizar cómo el profesorado mira profesionalmente los materiales curriculares se ha convertido en una línea de investigación reciente (Amador et al., 2017; Bernabeu et al., 2021; Dietiker et al., 2018; Ivars et al., 2020; McDuffie et al., 2018). Sin embargo, está proporcionando información relevante para entender cómo el profesorado se relaciona con los recursos curriculares a su alcance y cómo los utiliza en el diseño de actividades.

En Costa Rica, durante el 2012 se aprobó un currículo articulado alrededor de diferentes dimensiones que enfatizan la resolución de problemas y las situaciones contextualizadas (Alfaro et al., 2013; Ruiz, 2015) y establece cinco áreas de conocimiento: números, geometría, medidas, relaciones y álgebra, probabilidades y estadística (MEP, 2012). Cada una presenta una representatividad distinta según el ciclo escolar. En particular, el área de medidas, la cual se va a tratar en este artículo, aparece como contenido en la educación primaria y como temática transversal en la educación secundaria. La implementación del nuevo currículo ha generado un desafío para las personas docentes y ha puesto de manifiesto la necesidad de desarrollar nuevas competencias profesionales.

En este contexto, este estudio se centra en explorar cómo un grupo de docentes en activo de Costa Rica “miran profesionalmente” los materiales curriculares y el pensamiento matemático del estudiantado en el área de medida.

La medida en el currículo vigente de Costa Rica

El enfoque principal de los Programas de Estudio de Matemáticas (PEM) es la resolución de problemas planteados en contextos reales (MEP, 2012). En el área de medidas esta contextualización debe darse de manera natural por su utilidad en las actividades cotidianas. Es decir, las actividades o situaciones que se le planteen al estudiantado deben tener significado y no ser construidas de manera artificial o presentar situaciones matemáticas abstractas, disfrazadas o incrustadas en un contexto real (Ruiz, 2015).

De acuerdo con el Ministerio de Educación Pública (MEP) (2012), “resolver problemas en contextos reales ofrece significados, sentido de utilidad y medios diversos para poner en juego las capacidades y habilidades matemáticas, y permite andamios para la construcción de los aprendizajes desde lo concreto hacia lo abstracto” (pp. 36-37). Este currículo apuesta por formar ciudadanos y ciudadanas con habilidades para desarrollarse en la vida cotidiana, donde sean capaces de resolver situaciones problemáticas que surjan en la cotidianidad.

Los PEM establecen en cada área habilidades generales y específicas según el nivel académico. Una habilidad “es una capacidad o un saber hacer en relación con un objeto matemático (concepto o procedimiento)” (MEP, 2012 p. 22). Las habilidades no deben verse como fines logrados o no, sino como expectativas de aprendizaje que se pueden alcanzar de manera gradual. Las habilidades específicas se plantean como expectativas a corto plazo en cada año escolar y las generales, para el ciclo escolar (en Costa Rica se trabaja con dos ciclos escolares en educación primaria).

De forma complementaria, se presentan los procesos matemáticos como aquellos que realizan las personas al desarrollarse en las distintas áreas de las matemáticas: razonar y argumentar, plantear y resolver problemas, comunicar, conectar y representar (MEP, 2012). Por tanto, se vuelve imprescindible que docentes en activo las conozcan y puedan discernir si una actividad de un libro de texto o encontrada en la web corresponde con las habilidades o procesos a desarrollar planteados en los PEM.

Esta investigación se centra en el área de medidas, integrada por las magnitudes de longitud, moneda, peso, tiempo, capacidad, superficie, volumen, temperatura y sus medidas; además, de la medida del almacenamiento digital. Las habilidades generales que el alumnado debe tener al terminar la educación primaria en el área de medidas son: realizar mediciones; estimar medidas, aplicar el sistema métrico decimal y aplicar la medición en diversos contextos (MEP, 2012, p. 237).

“Mirar profesionalmente” los materiales curriculares y el pensamiento matemático del estudiantado en el área de medidas

“Mirar profesionalmente” los materiales curriculares (curricular noticing) se ha conceptualizado como la forma en la que el personal docente da sentido a las características de los materiales curriculares escritos o digitales y considera cómo estos pueden generar oportunidades de aprendizaje en su alumnado (Dietiker et al., 2018). En particular esta competencia implica (i) reconocer aspectos relevantes del contenido matemático en los materiales curriculares, (ii) interpretar las oportunidades de aprendizaje que propicia cada material curricular y (iii) decidir cómo usar dichos materiales curriculares en el diseño de una lección o secuencia de actividades.

La competencia “mirar profesionalmente” el pensamiento matemático del estudiantado ha sido conceptualizada por Jacobs et al. (2010) como tres destrezas interrelacionadas: (i) identificar detalles matemáticos importantes en las estrategias de solución de quien aprende; (ii) interpretar el pensamiento matemático de estudiantes con base en los detalles identificados y (iii) decidir cómo continuar con la instrucción considerando la comprensión matemática de cada persona inferida.

De manera específica, y en relación con el área de medida, investigaciones previas con estudiantes de enseñanza de educación infantil como la de Callejo et al. (2022) y Moreno et al. (2021) muestran que “mirar profesionalmente” el pensamiento matemático de los estudiantes depende de los elementos matemáticos que la persona docente en formación considera al interpretar la comprensión de la magnitud longitud y su medida del estudiantado (es decir, de su conocimiento de matemáticas). Cuando el profesorado en formación consideraba elementos matemáticos relacionados con la magnitud y con la medida simultáneamente, mostraban mayor capacidad de proponer actividades matemáticas para apoyar la progresión del alumnado (Callejo et al., 2022).

En Callejo et al. (2022) se identificaron tres perfiles de futuros docentes de educación infantil caracterizados por la forma de utilizar la información sobre una trayectoria hipotética de aprendizaje (THA) de la magnitud, longitud y su medida, cuando interpretaban el pensamiento matemático de las personas estudiantes. Por otra parte, las investigaciones citadas también señalan dificultades de las personas docentes en formación al usar su conocimiento sobre el aprendizaje del alumnado para interpretar la comprensión de ellos y diseñar actividades que apoyen su aprendizaje (Moreno et al., 2021).

El presente estudio contribuye a esta línea de investigación, al aportar datos de cómo las personas docentes en activo “miran profesionalmente” el pensamiento matemático del estudiantado en el área de medidas (y no solo con foco en la magnitud longitud y su medida) y cómo miran los materiales curriculares; es decir, cómo interpretan el potencial de actividades matemáticas escolares según la información derivada de la propuesta curricular vigente en Costa Rica (PEM) y deciden usarlas de acuerdo con las oportunidades que pueden brindar en el aula.

Las preguntas de investigación formuladas para el estudio son:

· ¿Cómo docentes en activo interpretan el pensamiento matemático de los y las estudiantes en el área de medidas?

· ¿Cuáles actividades (decisiones de enseñanza) plantean las personas docentes en activo en el área de medidas?

· ¿Cómo el profesorado en activo analiza las actividades del área de medidas teniendo en cuenta la información de los PEM?

Método

Esta investigación se clasifica como cualitativa de corte descriptivo, ya que pretende dar a conocer una realidad sin intervenir en esta, procura hacer una descripción de cómo las personas docentes en ejercicio “miran profesionalmente” los materiales curriculares y el pensamiento matemático del estudiantado relacionado con el área de medida.

Participantes e instrumento

Las personas participantes fueron 18 docentes en activo de instituciones de educación primaria públicas de Costa Rica, ubicada en la Gran Área Metropolitana (16 mujeres y 2 hombres). En el momento de la recolección de los datos, diez contaban con al menos 15 años de laborar en educación primaria y, solo, dos tenían menos de cinco años de experiencia.

Los participantes resolvieron un cuestionario conformado por un total de 12 ítems (Tabla 1) que se relacionaban con diferentes magnitudes y su medida: moneda (ítems 8a y 8b), longitud (ítems 9a y 9b), longitud y superficie (ítems 10a, 10b, 12a, 12b), masa (ítems 11a y 11b), medidas de información digital (ítem 13) y capacidad, masa y tiempo (ítem 14).

Todos estos tenían tres focos: (i) analizar el pensamiento matemático del estudiantado sobre magnitudes y sus medidas a partir de las respuestas a las actividades matemáticas, (ii) proponer actividades para apoyar el progreso en la comprensión de las magnitudes y sus medidas y (iii) analizar actividades relacionadas con magnitudes y sus medidas desde las referencias del currículo. Los dos primeros focos son afines a la competencia “mirar profesionalmente” el pensamiento matemático del alumnado. Y el tercer foco pretendía determinar en qué medida el personal docente usaba las dimensiones propuestas por la reforma curricular para el análisis de las actividades (habilidades generales y específicas, y procesos matemáticos).

Tabla 1. Ítems del cuestionario clasificados según el foco

Foco del ítem	Ítems del cuestionario	Total (12)
Analizar las respuestas del estudiantado	10a, 12a	2
Diseñar actividades matemáticas	8b, 9b, 12b	3
Analizar actividades matemáticas	8a, 9a, 10b, 11a, 11b, 13, 14	7

Nota: elaboración propia.

A continuación, se describen los ítems del cuestionario en relación con la magnitud implicada. La Figura 1 muestra los ítems 8a y 8b, centrados en la moneda. Además, se presenta una situación cotidiana de compra en la cual se indica la cantidad de dinero que se tiene y el total de la compra. La pregunta se centra en mostrar con cuáles billetes se puede pagar (cuestión I), y dos opciones de cantidad de billetes para dar el cambio (cuestión II). El ítem 8a solicita indicar el conocimiento previo que el o la estudiante debe tener para resolver la actividad, y el 8b proponer una actividad para quienes puedan presentar dificultades en la actividad propuesta.

Figura 1. Ítems 8a y 8b

Fuente: elaboración propia.

Esta actividad le exige al estudiantado (i) reconocer los diferentes billetes como unidades de medida de una cierta cantidad de dinero, y (ii) que una cantidad de dinero no cambia, aunque se modifique la agrupación dada por diferentes billetes y monedas. Es decir, la resolución se apoya en el conocimiento del estudiantado de los diferentes “agrupamientos” (unidades) que representan los distintos tipos de monedas en Costa Rica (Tabla 2).

Tabla 2. Billetes y monedas del colón (₡) costarricense que determinan diferentes “unidades” de medida

Billetes	₡1000; ₡2000; ₡5000; ₡10 000; ₡20 000
Monedas	₡5; ₡10; ₡25; ₡50; ₡100; ₡500
Fracción	100 céntimos

Nota: fuente elaboración propia.

Por su parte, las diferentes respuestas posibles (diversas formas de representar con billetes y monedas la cantidad que el dependiente debe devolver) amplía la oportunidad de reconocer la comprensión del alumnado con respecto a la conservación de la cantidad, aunque se represente con diferentes monedas y billetes. También está vinculado en esta actividad la relación inversa entre el valor de la unidad y el número de unidades necesarias para representar una cantidad. Es decir, a mayor valor del billete/moneda, menos cantidad de billetes/monedas se necesitan para una determinada cantidad/valor.

En la Figura 2 se presentan los ítems 9a y 9b que abordan el tema de longitud. Se muestra una actividad matemática escolar extraída de un libro de texto utilizado en Costa Rica y se espera que las personas docentes detecten que el contexto empleado en la actividad es incrustado, de acuerdo con el currículo costarricense, pues cuando se habla de desplazamiento de una caminata no se utilizan unidades de medida como decámetros y hectómetros. Además, se les solicita diseñar una actividad contextualizada para desarrollar dos habilidades específicas, relacionadas con la longitud, presentes en los PEM para educación primaria: realizar conversiones entre múltiplos y submúltiplos de la unidad de medida y resolver situaciones problema donde se utilice este tipo de medida (MEP, 2012).

Figura 2. Ítems 9a y 9b

Fuente: elaboración propia.

En la Figura 3 se presentan los ítems 10a y 10b relacionados con longitud y superficie. Se muestra una situación cotidiana donde una familia debe realizar la compra de un sillón para su sala de estar; para ello debe considerar el espacio disponible y dos posibles sillones de la tienda. En el ítem 10a se presentaba la respuesta de un o una estudiante a la actividad y la persona docente debe determinar si había resuelto el problema de manera satisfactoria. La respuesta de o la estudiante es incorrecta, pues solo empleó la superficie disponible en la sala y el área de la base del sillón, sin considerar las dimensiones de este y el espacio por donde debía ingresarlo a la casa. El ítem 10b le solicita a la persona docente indicar el uso que haría de la actividad propuesta para generar una discusión relacionada con el uso de las distintas temáticas del área de medidas en la cotidianidad.

Figura 3. Ítems 10a y 10b

Fuente: elaboración propia.

Los ítems 12a y 12b (Figura 4) también están relacionados con la longitud y superficie. Se presenta una actividad escolar de 5.º año que refleja una situación cotidiana, donde, a partir de la descripción de unos datos (mantel rectangular con el lado más largo de 2 metros y el otro 50 cm menos), se pide verificar dos afirmaciones.

La cuestión planteada a las personas docentes coloca el foco en el reconocimiento de los errores cometidos por tres estudiantes y en el diseño de una actividad para ayudar a un o una estudiante a superar su dificultad. Aparecen dos tipos de errores: (i) procedimentales, si comete errores al realizar operaciones aritméticas o cuando compara medidas con distinta unidad de medida debido a descuidos al momento de cumplir con la comparación; y ii) conceptuales, si están relacionados con los conocimientos abordados; por ejemplo, no hace diferencia entre medida lineal y cuadrada, no calcula el perímetro de una figura o compara únicamente utilizando el perímetro.

Figura 4. Ítems 12a y 12b

Fuente: elaboración propia.

El estudiante 1 no usa de forma adecuada la unidad de medida para la magnitud longitud (emplea cm2 para referirse al perímetro, error conceptual) y compara solo considerando el perímetro (error conceptual). El estudiante 2 realiza cálculos correctos para transformar los metros en centímetros, pero para calcular el perímetro del rectángulo utiliza solo dos de los lados, lo cual evidencia que no comprende el concepto de perímetro (error conceptual). El o la estudiante 3 traslada correctamente la información desde el contexto para determinar el perímetro de la tela (trozo de tela cuadrada 2x2) y del mantel (forma rectangular 2x1.5). Sin embargo, tiene dificultades en el uso de unidades de medida (error procedimental).

En la Figura 5 se presentan los ítems 11a y 11b relacionados con la masa. En el 11a se le solicita a la persona docente indicar al menos dos habilidades presentes en el PEM que se estarían estimulando. Algunas de las habilidades específicas que se pueden citar son: utilizar el kilogramo como unidad de medida, medir pesos utilizando el kilogramo y sus divisiones (1/4, ½ y 3/4), estimar y comparar medidas de peso, realizar conversiones entre múltiplos y submúltiplos de la unidad de medida (peso), resolver situaciones problemas donde se utilice este tipo de medida (peso). En el 11b cada docente debe describir los procesos de pensamiento que se activarían con la actividad. Por ejemplo, se podía elegir el proceso Comunicar, debido a que un o una estudiante puede compartir la respuesta que obtuvo con sus pares y justificar cómo llegó a dicha respuesta. Otro de los procesos que puede elegirse es la representación, y justificar que para resolver el problema podría interpretar que 750 gr. de queso es lo mismo que ¾ kg, pasando de una representación a otra.

Figura 5. Ítems 11a y 11b

Fuente: elaboración propia.

La Figura 6 muestra el ítem 13 centrado en medidas de información digital. Se presenta una situación cotidiana donde se deben realizar conversiones de una unidad de medida que no es parte de las citadas en los PEM, pero presente en la cotidianidad. Las personas docentes deben citar cuáles conocimientos se podrían favorecer con el trabajo de esta situación (utilidad de los conocimientos abordados en otros niveles de la formación). Se espera que indiquen que, aunque en secundaria el tema de medidas no se aborda de manera explícita sino de forma transversal, es muy importante que el alumnado pueda realizar conversiones de las distintas unidades de medida que se abordan en educación primaria (longitud, moneda, peso, tiempo, capacidad, volumen, tiempo, superficie, temperatura y ángulos) y aquellas que intervienen en su cotidianidad para resolver situaciones en las distintas áreas de las matemáticas.

Figura 6. Ítem 13

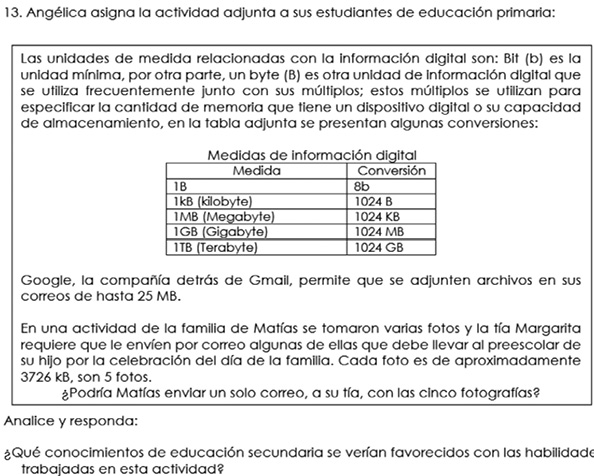
Fuente: elaboración propia.

Por último, el ítem 14 está relacionado con la medida de la masa, la capacidad y el tiempo (Figura 7). En este se presenta una situación cotidiana donde se deben realizar algunas conversiones y cálculos básicos para tomar decisiones relacionadas con la salud. Las personas docentes deben identificar los conceptos implicados para realizar la actividad. Algunos de estos son: unidad de medida (litro), múltiplos y submúltiplos del litro, relación entre la unidad de medida y la cantidad de unidades de medida.

Figura 7. Ítem 14

Fuente: elaboración propia.

El cuestionario pasó por varias etapas de validación. En la primera, según el criterio de las personas expertas, esta fue realizada por tres docentes universitarios relacionados con matemática educativa, una docente de educación primaria pensionada y una docente de matemática que imparte clases de esta asignatura en primaria. Se les facilitó el cuestionario y un instrumento de validación construido para este estudio. En la segunda etapa, se llevó a cabo una prueba piloto, la cual se ejecutó con tres docentes de educación primaria en activo. Tras realizar los cambios sugeridos por las personas encargadas de la primera validación y realizar mejoras de acuerdo con los resultados obtenidos en la prueba piloto, el cuestionario se sometió a la valoración de otra docente universitaria especializada en formación docente.

Análisis

El análisis de los datos se llevó a cabo en dos etapas. En la primera, tres investigadores analizaron independientemente una muestra de respuestas a cada ítem para identificar las características en las respuestas del profesorado. Estas características fueron refinadas según se iban analizando el resto de las respuestas al ítem. Las discrepancias fueron discutidas para buscar evidencias desde las diferentes respuestas que apoyaran las características generadas hasta llegar a un consenso. Como ejemplo, la Tabla 3 presenta las características identificadas en el ítem 12a.

Tabla 3. Características de las respuestas dadas por las personas docentes al ítem 12a: analizar las respuestas del alumnado

Características de las respuestas dadas		Ejemplo (evidencia)
Estudiante 1
E1.1	No identifica como lineal la unidad de medida para el perímetro.	D2
E1.2	Compara únicamente. considerando el perímetro.	No averiguó el área del rectángulo ni del cuadrado D17
Estudiante 2
E2.1	Para el perímetro no utiliza la suma de todos los lados.	D2
Estudiante 3
E3.1	Mezcla de unidades de medida (metro y centímetro).	D9
NR	Considera que no se cometieron errores, no contesta o su argumento es inválido.

Nota: elaboración propia.

En la segunda etapa del análisis, se agruparon las características de los ítems correspondientes a cada uno de los focos citados anteriormente: (i) analizar el pensamiento matemático de los y las estudiantes, (ii) proponer actividades para apoyar la progresión de la comprensión del alumnado, y (iii) estudiar las actividades para generar categorías que permitieran determinar y evidenciar la manera en la que cada docente miraba los materiales curriculares y el pensamiento matemático de sus estudiantes. Estas categorías y subcategorías dan respuesta a las preguntas de investigación formuladas, además se presentan y describen en el apartado de resultados (ver tablas 4-8).

Resultados

Los resultados se presentan de acuerdo con los focos para dar respuesta a las preguntas de investigación. En primer lugar, se presentan los resultados relativos a cómo cada docente interpreta las respuestas de sus estudiantes; es decir, cómo descifran el pensamiento matemático en el área de medidas. En segundo lugar, los resultados sobre cómo decidían sobre la instrucción al diseñar actividades en el área de medidas. Finalmente, se muestran los resultados relativos a cómo el profesorado analiza las actividades en el área de medidas teniendo en cuenta la información de los PEM.

Interpretar las respuestas del estudiantado

En la segunda etapa del análisis se generaron dos categorías sobre cómo cada docente interpretaba las respuestas de sus estudiantes: (i) docentes que identificaron errores en las respuestas y (ii) docentes que no identificaron errores.

Las respuestas de los y las docentes que identificaron errores en las soluciones realizadas por sus alumnos fueron agrupadas en tres subcategorías: i) identifica errores procedimentales (en los que la persona estudiante compara medidas con distinta unidad de medida o comete errores al realizar operaciones básicas), ii) identifica errores conceptuales (relacionados con los conceptos que intervienen en la resolución de la actividad; por ejemplo, no diferencian entre medida lineal y cuadrada, no considera todos los lados del rectángulo para calcular el perímetro, compara únicamente utilizando el perímetro) e iii) identifica errores al no tener en cuenta el contexto real del problema.

En la Figura 8 se muestra la respuesta para el ítem 12a (estudiante 1), en la que el o la docente identifica un error conceptual en la respuesta al no usar adecuadamente las unidades de medida (da el valor del perímetro acompañado con una unidad cuadrada).

Figura 8. Respuesta al ítem 12a (estudiante 1) en la que se identifica un Error conceptual

Fuente: elaboración propia.

La Figura 9 muestra la respuesta de una docente al ítem 10a, clasificada como “errores al no tener en cuenta el contexto real del problema”. Esta docente identificó que una de las opciones dadas “no entraba por la puerta de la casa”.

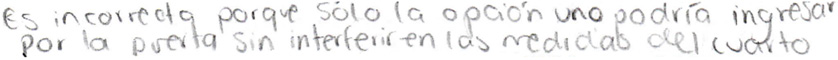
Figura 9. Respuesta al ítem 10a en la que se identifica que el o la estudiante no tiene en cuenta el contexto real del problema

Fuente: elaboración propia.

Por su parte, las respuestas de las personas docentes que no identificaron los errores se agruparon en tres subcategorías: (i) considera que sus estudiantes no habían cometido errores, (ii) identifica que la respuesta es incorrecta pero la justificación proporcionada no es adecuada y (iii) respuestas en blanco o sin sentido. Por ejemplo, en la respuesta expuesta en la Figura 10, dada al ítem 10, la docente consideró que la respuesta era correcta porque el alumno había calculado el área de la base del sillón y había elegido el de menor área para que la sala quedara mejor acomodada. Esta docente solo se fijó en los cálculos realizados por su estudiante, pero no consideró que se estaba resolviendo un problema contextualizado y, por tanto, se debía tomar en cuenta en qué medida la respuesta estaba teniendo en cuenta el contexto.

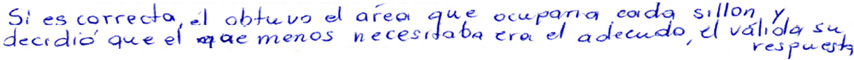
Figura 10. Respuesta dada al ítem 10a Considera que no habían cometido errores

Fuente: elaboración propia

La Tabla 4 presenta el número de respuestas distribuidas según las categorías y subcategorías generadas para los ítems de interpretar las producciones del estudiantado.

Tabla 4. Frecuencia para los ítems de interpretar las producciones del estudiantado

Categoría		Ítems
	Subcategorías	10a	12a
			E1	E2	E3
Identifica errores en las respuestas dadas	Errores procedimentales	-	-	-	5
	Errores conceptuales	-	12	12	5
	Errores al no interpretar el contexto	3	-	-	-
No identifica los errores en respuestas dadas	Considera que no tiene errores	11	-	-	-
	Identifica la respuesta incorrecta, pero la justificación no es adecuada	2	3	2	-
	Respuestas en blanco o sin sentido	2	3	4	8
Total		18	18	18	18
E1: estudiante 1, E2: estudiante 2, E3: estudiante 3 en el ítem 12a

Nota: elaboración propia.

Se observa un elevado número de docentes que no identificó el error cometido por el o la estudiante en el ítem 10a, al no considerar el contexto real del problema. Esto podría explicarse porque los contextos reales en las clases son poco utilizados, lo cual hace que la persona docente se fije solo en la corrección de los cálculos realizados. Además, asumen que sus estudiantes deben emplear los datos del problema de manera directa haciendo cálculos, y no analizan si las condiciones dadas en la actividad son viables.

En el ítem 12a se detectó un mayor número de docentes que fueron capaces de identificar al menos uno de los errores conceptuales del E1 (no identifica la unidad de medida para el perímetro como lineal) y del error conceptual cometido por E2 (para el perímetro no utiliza la suma de todos los lados). Mientras que un número menor de participantes detectó el error procedimental del E3 (mezcla de unidades de medida, metro y centímetro). En este caso, cinco docentes consideran que E3 comete un error conceptual al no realizar la comparación ayudado con la superficie del mantel y del trozo de tela dado.

Diseñar actividades matemáticas

Se generan dos categorías en relación con las actividades que plantean las personas docentes: (i) propone una actividad en correspondencia con la habilidad o dificultad a solventar y (ii) no diseñan una actividad en correspondencia con la habilidad o dificultad a solventar. En esta última se consideraron también a quienes dejaron en blanco la pregunta. En total los y las docentes propusieron 34 actividades relacionadas con una habilidad específica o con el interés por solventar la dificultad de un o una estudiante. En la Tabla 5 se presentan el total de las actividades según las categorías generadas.

Tabla 5. Número de actividades propuestas por las personas docentes

Categorías de análisis	Ítems
	8c	9b	12b
			E1	E2	E3
Plantea una actividad en correspondencia con la habilidad o dificultad a solventar.	17	7	3	5	2
No plantea una actividad en correspondencia con la habilidad o dificultad a solventar.	1	11	8
Total	18	18	18
Nota: En el ítem 12 b) cada docente podía elegir solo una persona para plantear la actividad. E1: estudiante 1, E2: estudiante 2, E3: estudiante 3

Nota: elaboración propia.

Para los y las docentes que plantearon una actividad adecuada en relación con la habilidad o dificultad a solventar, se identificaron tres subcategorías: (i) actividades que incluían la manipulación de material concreto, (ii) actividades que envolvían diferentes representaciones (iii) actividades centradas en el uso de fórmulas y cálculos automatizados. Además, se analizó si la actividad diseñada tenía en cuenta situaciones reales. Cabe destacar que algunas de las propuestas podían ser incluidas en subcategorías diferentes. La Tabla 6 muestra las frecuencias de los diferentes tipos de actividades que el profesorado propuso.

Tabla 6. Frecuencia de actividades planteadas

Subcategorías de análisis	Ítems
	8c	9b	12b
			E1	E2	E3
Actividades que incluían el uso de material concreto.	15	4	3	5	1
Actividades que incluían distintas representaciones (verbal, dibujos, gráficas, simbólico, etc.).	2	3	2	3	0
Actividades centradas en el uso de fórmulas y cálculos automatizados.	-	3	-	-	2
Actividad relacionada con contextos reales.	12	4	0	0	0
Nota: en el ítem 12 b) cada docente podía elegir solo una persona estudiante para plantear la actividad E1: estudiante 1, E2: estudiante 2, E3: estudiante 3

Nota: elaboración propia.

Por ejemplo, para la subcategoría de actividades que incluían el uso de material concreto, la docente de la Figura 11, en el ítem 8b, consideró importante centrarse en la unidad de medida que significa el uso de los billetes y monedas. Para ello, pensaba emplear réplicas de monedas y billetes para que sus estudiantes se familiarizaran con las distintas denominaciones y situaciones donde deben pagar un monto de dinero específico.

Figura 11. Respuesta de Actividades que incluían el uso de material concreto

Fuente: elaboración propia.

La Figura 12 muestra un ejemplo de actividad que incluía la manipulación de material concreto en el ítem 12b para el estudiante 2. Esta docente había interpretado como error que solamente había sumado dos lados para obtener el perímetro. Para solventar esta situación, propone que el estudiante mida el contorno de diversos objetos para que comprenda el concepto de perímetro.

Figura 12. Respuesta de Actividades que incluían el uso de material concreto

Fuente: elaboración propia.

En cuanto a las actividades que incluían diferentes representaciones, la Figura 13 muestra un ejemplo de actividad propuesta en el ítem 12b para el estudiante 1. La docente interpretó que el estudiante cometía un error al utilizar una unidad cuadrada que no correspondía con la fórmula del perímetro, pues está sumando unidades lineales y plantea el uso de dibujos y recorridos para explicarlo. Además, también cita el uso de material concreto, una cuadrícula.

Figura 13. Respuesta de Actividades que incluían distintas representaciones

Fuente: elaboración propia.

Por último, la Figura 14 muestra un ejemplo de actividad centrada en el uso de fórmulas y cálculos mecanizados en el ítem 12b para el estudiante 3. En particular, esta docente piensa que se debe robustecer el aprendizaje de las fórmulas proporcionándoles una ficha, pues interpreta que el estudiante se equivocó al obtener el perímetro del rectángulo porque utilizó de manera errónea la fórmula (cabe destacar que el estudiante no cometió un error al obtener el perímetro)

Figura 14. Ejemplo de Uso de fórmulas y cálculos automatizados

Fuente: elaboración propia.

En cuanto al uso de contextos reales, en la Figura 15 se presenta una actividad propuesta para el ítem 9b, donde se le solicitaba a cada docente plantear una actividad contextualizada que ayudara en el desarrollo de las habilidades específicas, incluidas en los PEM (2012): realizar conversiones entre múltiplos y submúltiplos de la unidad de medida y resolver situaciones problemas donde se utilice este tipo de medida, ambas relacionadas con la longitud. La docente crea una situación donde una persona requiere enmarcar una pintura y para ello requiere madera, ella da las dimensiones de la pintura en centímetros y requiere que el estudiante conteste en metros, dicha situación aborda un contexto personal, según los diversos contextos definidos para el currículo costarricense (Ruiz, 2018).

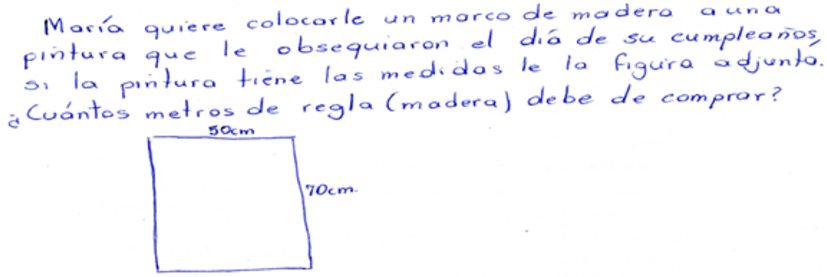
Figura 15. Respuesta de la categoría Actividad relacionada con contextos reales

Fuente: elaboración propia.

Las docentes tuvieron dificultades en el diseño de tareas sobre la longitud (9b) y la longitud y superficie (12b). Propusieron más actividades con material concreto que pudiera ayudar al estudiantado a superar las dificultades relativas a la idea de unidad cuando se usaba el contexto del dinero (monedas/ billetes) que con las otras magnitudes. Además, utilizaron contextos reales mayoritariamente al abordar el tema de la moneda y la longitud.

Analizar actividades

Los ítems sobre analizar actividades se centraban en: (i) identificar los contenidos implicados y los conceptos previos necesarios para realizar la actividad y (ii) la relación de la actividad con las habilidades y procesos cognitivos definidos por el currículo.

En relación con la primera categoría se generaron dos subcategorías: (i) docentes capaces de identificar los conceptos implicados en las actividades y (ii) docentes capaces de identificar únicamente algunos conceptos o ninguno.

La Figura 16 presenta la respuesta de una docente para el ítem 8a en la que se observa que identificó los conceptos previos requeridos para desarrollar la actividad: operaciones básicas, descomposición de cantidades y sistema monetario costarricense.

Figura 16. Ejemplo de docente que identificó conceptos previos implicados/requeridos

Fuente: elaboración propia.

Por otra parte, hubo docentes que fueron capaces de identificar algunos elementos, pero no en su totalidad. Por ejemplo, en el ítem 8a únicamente consideraron como conocimiento previo las operaciones básicas o identificaron las distintas denominaciones de monedas y billetes costarricenses.

Con respecto a la segunda categoría se generaron tres subcategorías: (i) docentes que identifican elementos generales definidos y planteados en el PEM (como ejes disciplinarios, procesos matemáticos, etc.); (ii) docentes que identifican elementos específicos definidos y planteados en el PEM (como conocimiento de cada nivel, habilidades específicas, etc.) y (iii) docentes que no identificaron elementos definidos y planteados en el PEM.

En la Figura 17 se muestra la respuesta de una docente en la categoría identifica elementos generales del currículo para el ítem 9a. Ella considera, según lo estipulado en los PEM, que el contexto de la actividad 9a es un contexto incrustado y, no real o cotidiano pues identificó que en la actividad cotidiana de caminar no se utilizan los decámetros ni los hectómetros para medir la distancia.

Figura 17. Ejemplo de Identifica elementos generales definidos en el currículo

Fuente: elaboración propia.

En el ítem 11a se pedía citar al menos dos habilidades que incentivaran la actividad como realizar conversiones entre múltiplos y submúltiplos de la unidad de medida (masa) y resolver situaciones problemas donde se utilice este tipo de medida (masa) (MEP, 2012). Además, como habilidades, de la asignatura de matemática, necesarias para resolverla también estarían implicadas: desarrollar y utilizar estrategias para el cálculo y la estimación, y resolver problemas del entorno en donde se haga uso de las operaciones básicas (MEP, 2012). La Figura 18 presenta la respuesta de una docente que identifica elementos específicos definidos en el currículo para la actividad mostrada en el ítem 11a.

Figura 18. Ejemplo de Identifica elementos específicos definidos en el currículo

Fuente: elaboración propia.

En cuanto a las dificultades de las personas docentes para analizar las actividades, en el ítem 9a consideraron que al tratarse de una caminata se hace referencia a una actividad cotidiana; sin embargo, no reflexionaron sobre las unidades de medida utilizadas. Aunque es correcto pensar que la caminata es una acción usual, el hecho de utilizar medidas no convencionales para calcular la distancia hace que se salga del contexto cotidiano.

En el ítem 11a, la mayor parte de las personas docentes no citaron habilidades específicas o generales definidas en los PEM, sino que enumeraron conocimientos (contenidos matemáticos), procesos de pensamiento (actividades cognitivas que realizan los y las estudiantes: razonar y argumentar, plantear y resolver problemas, comunicar, conectar y representar (MEP, 2012)) o habilidades genéricas o blandas para la vida, pero que no se relacionan directamente con la asignatura de las matemáticas. Lo anterior puede denotar un desconocimiento relacionado con la definición de habilidad presente en los PEM o un desconocimiento de las mismas habilidades que se deben desarrollar para el tema de medidas en educación primaria. Por ejemplo, la respuesta presentada en la Figura 19.

Figura 19. Ejemplo de No identifica diversos elementos planteados y definidos en el PEM

Fuente: elaboración propia.

Las tablas 7 y 8 muestran las frecuencias de las distintas categorías en los ítems de analizar actividades.

Tabla 7. Frecuencia de respuestas en los ítems de analizar actividades (conceptos implicados)

Categoría	Indicadores	Ítems
		8a	10b
Identificar contenidos matemáticos.	Determina los contenidos implicados y los conceptos previos requeridos para el desarrollo de una actividad.	2	1
No identifica o identifica solo algunos contenidos.	Identifica algunos contenidos, pero no en su totalidad.	16	12
	No identifica ningún contenido implicado en la actividad.	-	2
En blanco		-	3
Total		18	18

Nota: elaboración propia.

La mayoría de las personas docentes dieron respuestas incompletas. En relación con la identificación de habilidades y procesos cognitivos, la mayoría de docentes desconocía el significado de los procesos de pensamiento definidos en el currículo, lo cual evidencia algunas debilidades del conocimiento de las personas docentes sobre las diversas dimensiones del currículo que se pretende aplicar.

Tabla 8. Frecuencia de las respuestas en los ítems de analizar actividades (conocimiento del currículo)

Subcategorías	Ítems
	9a	11a	11b	13b	14b
Identifica elementos generales definidos en el currículo, por ejemplo: ejes disciplinarios, procesos matemáticos, etc.	7	-	4	6	13
Identifica elementos específicos definidos en el currículo, por ejemplo: conocimientos de cada nivel, habilidades específicas, etc.	-	7		-	-
No identifica los elementos del currículo.	9	10	13	6	2
No contesta.	2	1	1	6	3

Nota: elaboración propia.

Discusión y conclusiones

El objetivo de este estudio es explorar cómo un grupo de docentes en activo de Costa Rica mira profesionalmente los materiales curriculares y el pensamiento matemático del estudiantado en relación con el área de medida.

Los resultados sobre la interpretación de las respuestas de los y las estudiantes indican que el profesorado tiene dificultades para identificar las respuestas incorrectas de sus estudiantes por no considerar el contexto real del problema, característica establecidas en el currículo vigente de Costa Rica. Este resultado se relaciona con lo expuesto por Piñeiro et al. (2019) cuando indican que el cuerpo docente de educación primaria no está familiarizado con actividades matemáticas escolares donde cada estudiante deba articular una respuesta elaborada o un procedimiento de solución reflexionado sobre si la actividad no admite una solución directa.

Además, se observa que un grupo de docentes presenta dificultades para identificar los errores tanto conceptuales (relacionados con los conocimientos abordados, por ejemplo, el cálculo del perímetro, la asignación inadecuada de la unidad de medida y la comparación de superficies por medio exclusivo de perímetros) como procedimentales (operacionales y al comparar medidas con distintas unidades de medida) en las respuestas de los estudiantes. Este último resultado indica la dificultad de las personas docentes para interpretar el pensamiento matemático de los y las estudiantes, el cual puede estar vinculado a la necesidad de poseer un conocimiento especializado.

Un conocimiento de matemáticas especializado para la enseñanza en el área de medida puede favorecer la identificación de diferentes procedimientos utilizados por el estudiantado o errores cometidos (Buforn et al., 2022; Márquez et al., 2021). La necesidad de que las personas docentes posean un conocimiento especializado es vital porque únicamente identificaron que la respuesta era incorrecta sin interpretar el error cometido por cada estudiante o dando argumentos inválidos para justificar el error. Este resultado es importante ya que el profesorado debe ir más allá de dar una evaluación positiva o negativa de lo efectuado por sus estudiantes para poder identificar información sobre el proceso de comprensión del o la estudiante.

Así, el presente estudio contribuye a la literatura (Dindyal et al., 2021) al aportar información sobre cómo interpretan las personas docentes en activo (la mayoría de estudios previos están centrados con profesores en formación) y en un contexto matemático específico, diferentes magnitudes y su medida.

En relación con el diseño de actividades, la mayoría de las personas docentes considera importante el uso de materiales concretos y de contextos cotidianos en relación con las medidas de longitud o moneda, que son las primeras por abordar según el PEM. Mientras que, con la medida de superficie que se trabajan en el II ciclo de la Educación General Básica (ciclo incluido en la educación primaria de Costa Rica) dejan de lado la cotidianidad en sus propuestas. Aunque fueron capaces de proponer diferentes actividades, se observan algunas dificultades: cuando se les solicitaba que la actividad tuviera un contexto cotidiano y no lo consideraban, o cuando se les pedía que esta se relacionara con una habilidad específica o que debía estar en concordancia con el pensamiento de las personas estudiantes que habían analizado y se lograba esta relación. Las dificultades con el diseño de actividades centradas en la comprensión de su estudiante se han mostrado en estudios previos como el de Ivars et al. (2020), Barnhart y van Es (2015) o Tyminski et al. (2020).

Ahora bien, resulta pertinente que quien imparte matemáticas pueda reconocer las características de las actividades basadas en los elementos del currículo vigente, pues así podrá adecuarlas las habilidades y conocimientos requeridos por las personas estudiantes según su año escolar (Dietiker et al., 2018; Bernabeu et al., 2021). En muchas ocasiones el profesorado trabaja con libros de texto donde las actividades planteadas se alejan de lo estipulado en el currículo. En esta situación, cuando se requiere proponer actividades específicas a un o una estudiante para que supere una dificultad, se pone de manifiesto la necesidad de la competencia docente vinculada con el análisis de las actividades en relación con el currículo y a las dificultades de cada estudiante.

Sin embargo, en esta investigación los resultados relativos al análisis de las actividades indican que quienes participaron muestran cierto grado de desconocimiento de los elementos del currículo, pues sus respuestas solían ser incompletas o confundieron los elementos curriculares. Por ejemplo, si se les pedía analizar los procesos de pensamiento citaban habilidades y si se les pedía la habilidad fomentada citaban los conocimientos. En los PEM una habilidad “es una capacidad o un saber hacer en relación con un objeto matemático (concepto o procedimiento)” (MEP, 2012 p. 22), mientras que los procesos matemáticos son: razonar y argumentar, plantear y resolver problemas, comunicar, conectar y representar (MEP, 2012). La diferenciación curricular entre habilidad y proceso matemático se mostró difícil para las personas docentes en el área de la medida. Este resultado es importante porque un o una docente en activo debe conocer lo estipulado en el currículo para poder plantear sus lecciones y lograr que sus estudiantes avancen.

Las limitaciones presentadas por el profesorado participante en este estudio evidencian la necesidad de desarrollar propuestas de formación continua para docentes de educación primaria en activo, donde se fomente el desarrollo de la competencia docente de “mirar profesionalmente” el pensamiento matemático de los estudiantes y “mirar profesionalmente” los materiales curriculares.

Una futura línea de investigación emergente a raíz de este estudio podría ser indagar cómo las personas docentes de educación primaria en activo planifican una clase relacionada con el tema de medidas, considerando los lineamientos del currículo vigente, cómo la implementan y cómo analizan el pensamiento matemático de sus estudiantes.

Financiamiento (Funding)

Universidad Nacional, Costa Rica. SIA 0082-16.

Universidad Nacional, Costa Rica. SIA 0339-22.

El programa de doctorado ¨Investigación Educativa¨ de la Universidad de Alicante, España (Marianela Alpízar Vargas).

Conflicto de intereses

Las personas autores declaran no tener algún conflicto de interés.

Declaración de la contribución de las personas autores

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo.

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: M. A. V. 100/3 %, C. F. V. 100/3 % y S. L. C. 100/3 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente [M. A. V.], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: www.doi.org/10.5281/zenodo.8251105

Referencias

Alfaro, A., Alpízar, M., Morales, Y., Salas, O. y Ramírez, M. (2013). La formación inicial y continua de docentes de matemáticas en Costa Rica. Cuadernos de Investigación y Formación en Educación Matemática, 8 (número especial), 131-179. http://revistas.ucr.ac.cr/index.php/cifem/issue/view/1281

Amador, J. M., Males, L. M., Earnest, D. y Dietiker, L. (2017). Curricular noticing: Theory on and practice of teachers’ curricular use. En E. Schack, M. Fisher y J. Wilhelm (Eds.), Teacher noticing: Bridging and broadening perspectives, contexts, and frameworks (pp. 427-443). Springer. https://doi.org/10.1007/978-3-319-46753-5_25

Barnhart, T. y van Es, E. (2015). Studying teacher noticing: Examining the relationship among pre-service science teachers’ ability to attend, analyze and respond to student thinking. Teaching and Teacher Education, 45, 83-93. https://doi.org/10.1016/j.tate.2014.09.005

Bernabeu, M., Moreno, M. y Llinares, S. (2021). Anticipating primary school students’ answers of hierarchical classifications tasks: Features of preservice primary teachers’ curricular reasoning. Acta Scientiae, 23(6), 121-146. https://doi.org/10.17648/acta.scientiae.6874

Buforn, A., Llinares, S. y Fernández, C. (2018). Características del conocimiento de los estudiantes para maestro españoles en relación con la fracción, razón y proporción. Revista Mexicana de Investigación Educativa, 23(76), 29-251.

Buforn, À., Llinares, S., Fernández, C., Coles, A., & Brown, L. (2022). Pre-service teachers’ knowledge of the unitizing process in recognizing students’ reasoning to propose teaching decisions. International Journal of Mathematical Education in Science and Technology, 53(2), 425–443. https://doi.org/10.1080/0020739X.2020.1777333

Callejo, M. L., Pérez-Tyteca, P., Moreno, M. y Sánchez-Matamoros, G. (2022). The use of a length and measurement HLT by pre-service kindergarten teachers’ to notice children’s mathematical thinking. International Journal of Science and Mathematics Education, 20, 597-617. https://doi.org/10.1007/s10763-021-10163-4

Dietiker, L., Males, L. M., Amador, J. M. y Earnest, D. (2018). Curricular Noticing: A Framework to Describe Teachers’ Interactions with Curriculum Materials. Journal for Research in Mathematics Education, 49(5), 521-532. https://doi.org/10.5951/jresematheduc.49.5.0521

Dindyal, J., Schack, E., Choy, B. H. y Gamora-Sherin, M. (2021). Exploring the terrains of mathematics noticing. ZDM Mathematics Education, 53(1), 1-16, https://doi.org/10.1007/s11858-021-01249-y

Fernández, C. y Choy, B. H. (2020). Theoretical lenses to develop mathematics teacher noticing. Learning, Teaching, Psychological, and social perspectives. En S. Llinares y O. Chapman (Eds.), International Handbook of Mathematics Teachers Education: Volume 2. Tools and Processes in Mathematics Teacher Education (vol. 12, pp. 337-360). Brill. https://doi.org/10.1163/9789004418967_013

Fernández, C., Llinares, S. y Rojas, Y. (2020). Prospective mathematics teachers’ development of noticing in an online teacher education program. ZDM Mahematics Education, 52(5), 959-972. https://doi.org/10.1007/s11858-020-01149-7

Fernández, C., Sánchez-Matamoros, G., Valls, J. y Callejo, M. L. (2018). Noticing students’ mathematical thinking: characterization, development and contexts. Advances in rese research in mathematics education, 13, 39-61. https://doi.org/10.35763/aiem.v0i13.229

Fisher, M. H., Thomas, J., Jong, C., Schack, E. O. y Dueber, D. (2019). Comparing preservice teachers’ professional noticing skills in elementary mathematics classrooms. School Science and Mathematics, 119(3), 142-149. https://doi.org/10.1111/ssm.12324

Ivars, P., Fernández, C. y Llinares, S. (2020). Uso de una trayectoria hipotética de aprendizaje para proponer actividades de instrucción. Enseñanza de las Ciencias, 38(3), 105-124. https://doi.org/10.5565/rev/ensciencias.2947

Jacobs, V. R., Lamb, L. C. y Philipp, R. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169-202. https://doi.org/10.5951/jresematheduc.41.2.0169

Llinares, S. y Fernández, C. (2021). Mirar profesionalmente la enseñanza de las matemáticas: características de una agenda de investigación en Didáctica de la Matemática. La Gaceta de la RSME, 24(1), 185-205.

Márquez, M., Fernández, C. y Callejo, M. L. (2021). Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions. Mathematics, 9, 3163. https://doi.org/10.3390/math9243163

McDuffie, A. R., Choppin, J., Drake, C. y Davis, J. (2018). Middle school mathematics teachers’ orientations and noticing of features of mathematics curriculum materials. International Journal of Educational Research, 92, 173-187. https://doi.org/10.1016/j.ijer.2018.09.019

Ministerio de Educación Pública (MEP). (2012). Programas de Estudio en Matemáticas para la Educación General Básica y el Ciclo Diversificado. San José, Costa Rica: autor.

Moreno, M., Sánchez-Matamoros, G., Callejo, M. L., Perez-Tyteca, P. y Llinares, S. (2021). How prospective kindergarten teachers develop their noticing skills: the instrumentation of a learning trajectory. ZDM Mathematics Education, 53, 57-72. https://doi.org/10.1007/s11858-021-01234-5

Piñeiro, J. L., Castro-Rodríguez, E. y Castro, E. (2019). Concepciones y creencias de profesores de primaria sobre problemas matemáticos, su resolución y enseñanza. Avances de Investigación en Educación Matemática, (16), 57-72. https://doi.org/10.35763/aiem.v0i16.253

Ruiz, A. (2015). Reforma de la Educación matemática en Costa Rica. Balance y perspectivas. Cuadernos de Investigación y Formación en Educación Matemática, 13, 15-30. https://revistas.ucr.ac.cr/index.php/cifem/issue/view/1866

Ruiz, A. (2018). Evaluación y pruebas nacionales para un Currículo de Matemáticas que enfatiza capacidades superiores. Comité Interamericano de Educación Matemática: México.

Tyminski, A. M., Simpson, A. J., Land, T. J., Drake, C. y Dede, E. (2020). Prospective elementary mathematics teachers’ noticing of childrens’ mathematics: a focus on extending moves. Journal of Mathematics Teacher Education, 24, 533-561. https://doi.org/10.1007/s10857-020-09472-2

van den Kieboom, L. A., Magiera, M. T. y Moyer, J. C. (2017). Learning to notice student thinking about the equal sign: K-8 preservice teachers’ experiences in a teacher preparation program. En E. O. Schack et al. (eds.), Teacher Noticing: Bridging and Broadening Perspectives, Contexts, and Frameworks (pp. 141-159). Springer International Publishing AG.
https://doi.org/10.1007/978-3-319-46753-5_9

Weyers, J., König, J., Scheiner, T., Santagata, R. y Kaiser, G. (2023). Teacher noticing in mathematics education: a review of recent developments. ZDM Mathematics Education.
https://doi.org/10.1007/s11858-023-01527-x

---

1. 1* Autor para correspondencia

   Marianela Alpízar-Vargas, marianela.alpizar.vargas@una.ac.cr, https://orcid.org/0000-0002-3515-1971

   Ceneida Fernández, ceneida.fernandez@ua.es, https://orcid.org/0000-0002-4791-9247

   Salvador Llinares, sllinares@ua.es, https://orcid.org/0000-0002-0801-316X

   Universidad Nacional, Heredia, Costa Rica.

2. 2 Universidad de Alicante, Alicante, España.