Selección y análisis de vídeos en la formación inicial del profesorado de educación matemática infantil: rúbrica R4

Selection and analysis of videos in the initial training of early childhood mathematics education teachers: the R4 Rubric

Seleção e análise de vídeos na formação inicial de professores de matemática na educação infantil: rubrica R4

Ainhoa Berciano1*, María Salgado2, Ángel Alsina3

Received: Aug/30/2023 • Accepted: Jan/23/2024 • Published: Jul/31/2024

Resumen [Objetivo] Aunque el uso de vídeos de aula no es un tópico novedoso en la formación inicial del profesorado de educación matemática infantil, todavía hay preguntas de investigación sin resolver asociadas, sobre todo, a criterios para seleccionar y analizar vídeos desde un enfoque didáctico y disciplinar. Desde esta perspectiva, la finalidad del artículo es diseñar y validar una rúbrica que sirva para este doble propósito. [Metodología] A partir de un paradigma de investigación cualitativo, se ha seguido un proceso 4x3, es decir, un método secuenciado en cuatro fases con tres pasos en cada una de ellas: 1) revisión, 2) creación, 3) contraste y evaluación, y 4) mejora. [Resultados] La versión definitiva de la rúbrica, denominada R4, consta de 28 ítems organizados en cuatro dimensiones: 1) rol docente, sobre la función que tiene cada docente en el aula; 2) respuesta del alumnado infantil en la tarea, sobre su actuación; 3) relaciones matemáticas, sobre el tipo de matemática; 4) recursos, sobre la gestión y uso de recursos-materiales humanos. Para cada dimensión se considera diversas subdimensiones, en total 16. [Conclusiones] Se concluye que la rúbrica R4 aborda aspectos fundamentales (rol docente, respuesta del alumnado infantil, relaciones matemáticas y recursos) en la labor docente de una maestra o maestro de educación infantil, lo cual permite analizar la práctica docente de un modo holístico y fundamentado. Palabras clave: educación matemática infantil; desarrollo profesional del profesorado; prácticas docentes; vídeos de aula; rúbrica. Abstract [Objective] Although the use of classroom videos is not a new topic in the initial training of early childhood mathematics education teachers, there are still unresolved research questions associated, above all, with criteria for selecting and analyzing these videos from both a didactic and disciplinary approach. From this perspective, the purpose of this article is to design and validate a rubric that serves this dual purpose. [Methodology] Based on a qualitative research paradigm, a 4x3 process has been followed, that is, a method sequenced in four phases with three steps in each one of them: 1) Review; 2) Creation; 3) Contrast and Evaluation; and 4) Improvement. [Results] The final version of the rubric, called R4, consists of 28 items organized in four dimensions: 1) Teaching role, on the role of the teacher in the classroom; 2) Response of children in the task to his/her performance; 3) Mathematical relations, on the type of mathematics; 4) and Resources, on the management and use of human resources and materials. For each dimension, several subdimensions are considered, 16 in total. [Conclusions] It is concluded that the R4 rubric addresses fundamental aspects (Teaching role, Childrens’ response, Mathematical relations and Resources) in the teaching work of an early childhood education teacher, which allows analyzing the teaching practice in a holistic and justified way. Keywords: Early childhood mathematics education; teacher professional development; teaching practices; classroom videos; rubric. Resumo [Objetivo] Embora o uso de vídeos em sala de aula não seja um tópico novo na formação inicial de professores de matemática da educação infantil, ainda há questões de pesquisa não resolvidas associadas, sobretudo, aos critérios de seleção e análise de vídeos a partir de uma abordagem didática e disciplinar. A partir dessa perspectiva, o objetivo do artigo é projetar e validar uma rubrica que atenda a essa dupla finalidade. [Metodologia] Com base em um paradigma de pesquisa qualitativa, foi seguido um processo 4x3, ou seja, um método sequenciado em quatro fases com três etapas em cada uma delas: 1) revisão, 2) criação, 3) contraste e avaliação, e 4) aprimoramento. [Resultados] A versão final da rubrica, denominada R4, consiste em 28 itens organizados em quatro dimensões: 1) papel do professor, sobre a função que cada professor tem na sala de aula; 2) resposta dos alunos à tarefa, sobre seu desempenho; 3) relações matemáticas, sobre o tipo de matemática; 4) recursos, sobre o gerenciamento e o uso de recursos humanos-materiais. Para cada dimensão são consideradas diversas subdimensões, totalizando 16. [Conclusões] Conclui-se que a rubrica R4 aborda os principais aspectos (função do professor, resposta dos alunos da educação infantil, recursos e relações matemáticas) no trabalho de ensino de um professor da educação infantil, o que permite uma análise holística e informada da prática de ensino. Palavras-chave: ensino da matemática na educação infantil; desenvolvimento profissional de professores; práticas de ensino; vídeos em sala de aula; rubrica.

Introducción

El uso de vídeos durante la formación inicial del profesorado es una herramienta valiosa para su desarrollo profesional docente y una ventana abierta a su futura profesión. Así, a pesar de que su uso como herramienta formativa no responde a un planteamiento metodológico novedoso, debido a que ya se usaban en la década de los años noventa (Guardia González, 1990), las investigaciones más recientes sí hacen hincapié en los beneficios de usar estos vídeos durante la formación inicial, sobre todo para poder observar distintas metodologías de enseñanza, ver el tratamiento de diversos contenidos, detectar las dificultades y errores que experimenta el alumnado, el uso de diferentes materiales, entre otros (Esteley et al., 2021; Rosales López, 2014).

Al considerar las posibilidades que ofrecen los vídeos durante la formación inicial del profesorado, ha ido aumentando la cantidad de vídeos en la red en referencia a las prácticas de enseñanza de las matemáticas (Azer et al., 2013), razón por lo cual se hace necesario analizar la pertinencia de estos, ya que pueden ser una buena herramienta informal (Ramírez, 2010).

Las investigaciones en Didáctica de las Matemáticas sobre la utilización de vídeos muestran la necesidad de que el o la docente haga una buena selección (Santos, 2018), con el propósito de generar conflicto cognitivo, reflexión y una buena transferencia al aula, por lo que resulta necesario describir cuáles componentes definen un buen vídeo para favorecer la reflexión personal del profesorado durante su formación inicial (Burgos et al., 2020).

Así, teniendo en cuenta la potencialidad formativa de los vídeos docentes, es indudable la importancia de contar con herramientas para promover el desarrollo profesional docente (Portugal et al., 2018); es decir, poder abordar con el profesorado en formación inicial todos los aspectos relevantes y modelos en los que fundamentar su futura práctica docente desde un punto de vista crítico y estructurado.

Desde esa perspectiva, el objetivo de este artículo es describir el proceso de construcción y validación de una herramienta que permita seleccionar vídeos docentes en el aula de educación matemática infantil y su valoración de manera sistemática. Esta herramienta, en forma de rúbrica, ha sido denominada R4 y está conformada por un sistema categórico dividido en cuatro dimensiones, con sus respectivos indicadores de medición.

Marco teórico

La formación inicial del profesorado de educación infantil es una de las etapas más importantes de cara a la futura profesión de este colectivo, en la cual, atendiendo a las competencias establecidas en la Orden ECI/3854/2007 (Ministerio de Educación y Ciencia, 2007), a lo largo de dicha etapa, las personas deben desarrollar habilidades que les permitan asumir tareas relacionadas con la gestión del aula, su entorno, la vida sana, entre otras, pero sobre todo fomentar el aprendizaje significativo; en concreto, adquirir las competencias que le faculten para

promover y facilitar los aprendizajes en la primera infancia, desde una perspectiva globalizadora e integradora de las diferentes dimensiones cognitiva, emocional, psicomotora y volitiva […], diseñar y regular espacios de aprendizaje en contextos de diversidad que atiendan a las singulares necesidades educativas de los estudiantes, a la igualdad de género, a la equidad y al respeto a los derechos humanos (p. 53736).

En este sentido, Alonso-Sainz (2019), en su estudio sobre los perfiles de egreso definidos por las universidades españolas para los grados de Magisterio, concluye que, una vez finalizada esta etapa formativa, el profesorado debe ser capaz de mediar (crear entornos de aprendizaje) y de gestionar (encargarse de tareas, organizar o planificar una acción, desarrollarla y crear actividades infantiles), entre otros.

Con el fin de conseguir este propósito, y al centrar el interés en la educación matemática, la formación inicial de docentes en la competencia matemática debe contribuir a la adquisición de estas y otras habilidades. Así, investigaciones previas ponen de manifiesto que para lograrlo es fundamental reforzar tanto la formación disciplinar como la didáctico-matemática, hecho completamente validado por medio del estudio de Alsina (2020), en el cual muestra que a nivel estatal existe una deficiencia notable en la formación didáctico-matemática (con un peso relativo del 2.5 % en los estudios, mayoritariamente) y una ausencia casi absoluta en matemática. Este hecho refuerza la necesidad de plantear tareas o actividades para mejorar la formación inicial didáctico-matemática de este colectivo y, en ese sentido, Joglar et al. (2021) destacan la importancia de conectar la formación inicial del profesorado de educación infantil con la práctica de aula.

Así, a pesar de que existen enfoques metodológicos muy diversos en la formación inicial del profesorado de educación infantil, como los recursos o materiales de distinta índole, si se pone en valor la conexión con la práctica de aula, uno de los medios o recursos para poder mostrar esta realidad es el uso de vídeos docentes. Este recurso, como ya se ha comentado en la introducción, no es novedoso en la formación inicial de profesorado; de hecho, en los años noventa se puso en valor su utilidad y potencialidad (Guardia González, 1990), pero debido a los avances tecnológicos de los últimos años, actualmente el acceso a estos vídeos es cada vez más factible.

Así, distintas investigaciones abordan las ventajas del uso de vídeos en la formación inicial del profesorado desde diversos ámbitos: creación, visionado, entre otros. Por un lado, sobre la creación, Bautista García-Vera (2013) afirma que elaborar videografías comunitarias en la formación del profesorado favorece, entre otros aspectos, el liderazgo; pues, en el proceso creativo, se aprende a estructurar las ideas que se desean comunicar. Por otro lado, acerca del visionado, el uso de los vídeos ayuda al profesorado en formación inicial a analizar las condiciones y elementos de la enseñanza-aprendizaje de la matemática, por medio de la observación, análisis, predicción y generalización (Callejo et al., 2007).

Al respecto, Llinares (2007) explicita que el uso de vídeos sobre la enseñanza de la matemática puede ayudarle al profesorado en formación inicial a reflexionar sobre tres aspectos: 1) la importancia de los contenidos como objetos de enseñanza-aprendizaje, 2) analizar el pensamiento matemático del alumnado a partir de sus respuestas en actividades matemáticas y 3) estudiar la gestión del profesorado, en contextos de aula reales, de los contenidos matemáticos y de las interacciones con su alumnado.

Santagata y Guarino (2011) detallan distintos tipos de vídeos y posibles actividades en la formación inicial del profesorado; entre ellos, vídeos de entrevistas con niños y niñas y otros de sesiones de aula. Además, afirman que el visionado de vídeos de aula sobre resolución de problemas ofrece la oportunidad de observar tanto el tipo de razonamiento y los métodos de resolución del alumnado, como la labor docente para usar las ideas del alumnado estableciendo relaciones entre conceptos y procedimientos; lo cual permite modelar prácticas eficientes.

En esta misma línea, Esteley et al. (2021) y Joglar et al. (2021) afirman que el uso de vídeos en la formación inicial del profesorado contribuye al desarrollo de la competencia noticing o mirada profesional, entendida como la capacidad de “prestar atención, reconocer y dar sentido a aspectos específicos emergentes de las interacciones en el aula” (Esteley et al., 2021, p. 65).

Aun así, son varias las dificultades que surgen del uso de vídeos como herramienta didáctica en la formación inicial del profesorado. Por un lado, no se puede obviar que el uso de este recurso como herramienta didáctica requiere de una planificación previa, en la cual se debe tener en cuenta la audiencia y el objetivo que se pretende lograr (García Matamoros, 2014). Además, según Coles (2019), otro de los problemas surge de una de las características del uso de vídeos docentes, por la cual se invita a la audiencia a comentar los detalles de lo visionado y a comentarlo basado en evidencias, razón por la cual resulta difícil establecer qué es “hablar basado en evidencias”. En este sentido, se torna necesario disponer de herramientas para realizar una observación sistemática de los vídeos docentes.

Así, Charalambous y Praetorius (2018), tras el análisis de las complementariedades y diferencias de un listado de 12 instrumentos para la observación, concluyen que es necesario crear categorías de análisis para estudiar mejor las prácticas en el aula matemática. En esta misma línea, Burgos et al. (2020) afirman la necesidad de que el profesorado disponga de instrumentos para analizar la pertinencia de los vídeos docentes.

Con el fin de responder a esta necesidad, en los últimos años se encontró varios instrumentos de observación o modelos de análisis de prácticas docentes matemáticas en la literatura: modelo de análisis de vídeos para identificar situaciones de interacción social en el aula de matemáticas vinculadas a procesos de construcción de conocimiento matemático (Planas, 2006), usado en Educación Secundaria; IOC-PROB, herramienta para la observación de la enseñanza de la probabilidad en Educación Primaria (Vásquez-Ortiz et al., 2020); POEMAT.es ―pauta de observación de la enseñanza de matemáticas en Educación Secundaria en España― (Studying and improving Mathematics instruction in secondary schools in Spain study group [grupo de estudio SiMiS], 2021); uso y análisis de la idoneidad didáctica desde el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos (EOS), en el cual Burgos et al. (2020), tras una experiencia de aula, pretenden que el profesorado en formación inicial analice la idoneidad didáctica de un vídeo sobre proporcionalidad en Educación Primaria, concluyen que el análisis del vídeo reveló errores e imprecisiones, pero la herramienta resulta compleja y necesita de un mayor número y variedad de vídeos de análisis, así como una mayor discusión colectiva.

Aun así, debido a la ausencia de trabajos que especifiquen una herramienta de observación de prácticas matemáticas en la formación inicial de profesorado de educación infantil tanto disciplinar como didáctica, en este artículo se presenta el diseño y validación de una rúbrica para ayudar a seleccionar y analizar de modo sistemático vídeos docentes de matemática para la formación inicial del profesorado en el aula infantil, que facilite por un lado la selección de vídeos y, por otro, el análisis sistemático de estos.

Metodología

Con el fin de cumplir con el objetivo de investigación, la creación y validación de una herramienta de selección y análisis de vídeos docentes para la formación inicial de profesorado de educación matemática infantil, se ha asumido el método cualitativo.

Así, para crear y validar dicho instrumento de selección de vídeos y el instrumento de análisis de estos, se ha seguido un proceso 4x3; es decir, un método secuenciado en cuatro fases (Fase 1: revisión, Fase 2: creación, Fase 3: contraste y evaluación, Fase 4: mejora), ReCreCEMe, con tres pasos en cada una de ellas. De este modo, se da una definición final de la herramienta, denominada R4.

En el siguiente diagrama de flujo (Figura 1) se puede apreciar las características de cada una de las fases antes mencionadas.

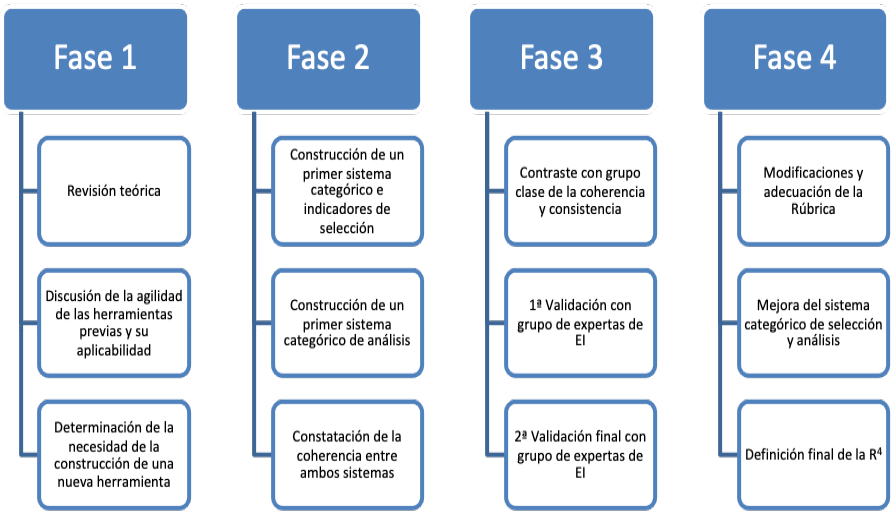
Figura 1. Fases de la creación de la rúbrica R4

Nota: fuente propia de la investigación.

En resumen, tras la revisión de la literatura se ha procedido a crear una primera versión de la rúbrica. Seguidamente, se han determinado los grupos de interés del uso de esta (alumnado, esto es, profesorado en formación inicial de educación infantil y profesorado e investigadores e investigadoras del área), se han establecido los instrumentos de evaluación que permitan extraer información relevante de los contrastes con los grupos de interés, se recolectaron los datos de dichos contrastes, el equipo investigador trianguló los resultados y, finalmente, se realizó una propuesta de mejora y elaboración definitiva de la rúbrica.

Selección de los grupos de interés

Para el contraste de la rúbrica se han considerado tres grupos de interés:

1. Alumnado del grado de educación infantil (esto es, profesorado en formación inicial de educación infantil): se ha elegido, por conveniencia, un grupo de 22 estudiantes de tercer curso de la asignatura “Pensamiento Matemático y su Didáctica” de la Universidad del País Vasco (UPV/EHU). Este colectivo no tiene formación previa en Matemáticas ni en Didáctica de la Matemática y la asignatura que se detalla es la única obligatoria del área de Didáctica de la Matemática que cursan a en todo el Grado, con un peso de 6 ECTS de los 240 ECTS que componen el total de asignaturas.

2. Profesorado y equipos de investigación con interés en la enseñanza-aprendizaje de la matemática en Educación Infantil: grupo de discusión conformado por 30 asistentes a la reunión intermedia del grupo de trabajo “Investigación en Educación Matemática Infantil” (IEMI), de la Sociedad Española de Investigación en Educación Matemática (SEIEM), en la Universidad Autónoma de Madrid (España) en marzo de 2023. En el grupo se encontraban personas de reconocido prestigio y una amplia experiencia en la investigación de la Didáctica de la Matemática.

3. Investigadores e investigadoras en formación inicial y educación infantil, con una proyección internacional: dos personas expertas de ámbito latinoamericano y cuatro de ámbito español (donde tres de estas no han estado involucradas en la validación grupal y una cuarta asistente en dicha validación, que permita realizar un contraste complementario a la validación grupal).

Análisis y resultados

Fase 1: revisión teórica

Tal como se ha descrito en el marco teórico, son varios los instrumentos que se usan para evaluar algunas herramientas didácticas, entre ellas, los vídeos (Burgos et al., 2020; Planas, 2006; Vásquez-Ortiz et al., 2020; Grupo de estudio SiMiS, 2021). Así, en esta primera fase, se ha analizado los enfoques desde los que se crean las herramientas de análisis de los estudios anteriormente citados y las categorías definidas en ellas, las cuales se describen a continuación:

• Burgos et al., 2020 crearon un instrumento enmarcado en el enfoque ontosemiótico, en el que se valora la ideoneidad del contenido matemático a través del análisis de la dimensión epistémica haciendo referencia, concretamente, a seis componentes: situaciones-problema, lenguajes, reglas, argumentos, relaciones entre objetos y articulación de significados. Las personas autoras, en su implementación con el alumnado en formación, señalan las dificultades en el manejo de la herramienta a nivel conceptual, a pesar de haber habido instrucción antes de su uso.

• Con respecto al instrumento de análisis de vídeos que presenta Planas (2006), se trata de una herramienta lineal y abierta, basada en conocimientos derivados de la interacción social. Señala seis fases, todas dependientes entre sí, estas son: el estudio y descripción del vídeo, la identificación de episodios con significados matemáticos, la búsqueda de procesos de reelaboración de los significados descubiertos, la caracterización de interacciones sociales, la elaboración de historias explicativas y la comparación de los episodios de revisión. La autora destaca el peso subjetivo de la herramienta y, por ello, la importancia de contrastar, comentar y comparar cada una de las fases en el proceso de análisis de vídeos.

• Vásquez-Ortiz et al. (2020) describen un instrumento de observación de clases de probabilidad en el cual discriminan cinco dimensiones que hacen referencia al tipo de tarea, al razonamiento, a las conexiones, a la comunicación y al lenguaje. A su vez, categorizan y describen estas dimensiones, simplificando la comprensión de la herramienta. A pesar de que hacer referencia al campo de la probabilidad pueda parecer una limitación, las dimensiones y categorías resultan fáciles de extrapolar a otros campos de las matemáticas.

• Por último, el grupo SiMis (2021) presenta una herramienta de análisis denominada POEMat.es, diseñada para identificar elementos de la práctica del profesor en educación secundaria observados a través de grabaciones de vídeo. El instrumento diferencia tres dimensiones: contenido matemático, didáctica de la matemática y gestión del aula. Para el análisis de estas dimensiones se explicita una serie de indicadores, que a su vez se categorizan según su valor de desempeño. A pesar de que el instrumento es considerado valioso para la formación del profesorado de matemáticas en secundaria, ya que este colectivo tiene dificultades para diferenciar lo que es “útil” y “no útil”, los autores plantean ejemplos ilustrativos para cada nivel de indicador de la herramienta con el fin de facilitar su interpretación.

Este análisis lleva a establecer ciertos nexos o dimensiones destacadas (a grandes rasgos) entre las herramientas mencionadas; entre ellas, la importancia de la gestión que realiza el o la docente en el aula, el entender el aprendizaje de la matemática como algo social y como un área conectada y, por último, la necesidad de profundizar en los significados matemáticos. A pesar de ello, los resultados mostrados en las propias investigaciones citadas evidencian que algunas de estas herramientas a veces resultan complejas de usar y, por ende, surge la necesidad de crear una nueva.

Fase 2: Creación de la primera versión de la rúbrica

Un primer análisis de las herramientas disponibles y de los objetivos docentes e investigadores del equipo da lugar a establecer criterios básicos para poder realizar la selección de los vídeos:

1. De aula reales.

2. Tiempo máximo de visionado: 10 minutos.

3. Que den pie para discutir y reflexionar sobre la función docente en el aula de matemáticas, tanto destacando aspectos positivos como negativos.

4. Que generen un conflicto en el modo de usar los materiales y recursos y cómo se plantea el paso de la concreción a la abstracción matemática.

Asociados a estos criterios de selección y al análisis realizado en la fase 1, sobre los posibles nexos de las herramientas ya existentes, se crea el primer sistema categórico de selección de vídeos. Los apartados 3 y 4 permiten establecer una primera categorización sobre los apartados fundamentales de selección de los vídeos, atendiendo a las siguientes tres dimensiones:

• Rol docente: permite distinguir la función del o la docente en el aula.

• Respuesta del alumnado en la tarea: identificar cómo actúa el alumnado.

• Relaciones matemáticas: analizar el tipo de matemática.

En paralelo, este primer sistema categórico de selección lleva implícita la creación del primer sistema categórico de análisis de vídeos:

• Rol docente:

• Si el tipo de comunicación es bidireccional (si se fomenta el diálogo) o unidireccional (imperativo, expositivo).

• ¿Cómo fomenta el desarrollo matemático?

• ¿Qué tipo de preguntas plantea?

• Respuesta del alumnado en la tarea:

• Tipo de participación en su aprendizaje (activo/pasivo).

• Relaciones matemáticas en la realización de la actividad:

• Contenidos y procesos matemáticos que emergen.

• Conexiones con otras áreas del conocimiento.

• Establecimiento del ciclo C-P-A.

Fase 3: contraste de la rúbrica

Primer contraste del análisis de dos vídeos que deberían cumplir los principios de los apartados 3 y 4, con grupo clase de alumnado.

Tras la selección de dos vídeos que cumplen los criterios establecidos, sin dar razonamientos de análisis, se realiza una dinámica de clase con el profesorado en formación inicial de 3.er curso del Grado de Maestro de Educación Infantil (un total de 22 participantes, que conforma el primer grupo de interés descrito en el apartado anterior), como actividad habitual de aula, para determinar cuáles ítems destacan en la valoración de una práctica docente matemática y, posteriormente, consensuarlo en el grupo-clase a partir de una dinámica individual-pequeño en un grupo de 4-5 personas (Figura 2).

Figura 2. Resultados del consenso de clase

Nota: fuente propia de la investigación..

Como se observa en la Figura 2, el profesorado en formación inicial menciona el papel del profesorado (Rol docente), la contextualización de la actividad (Relaciones matemáticas), el papel del alumnado (Respuesta del alumnado) y los recursos y gestión de estos. Por tanto, se propone un ajuste adecuado en las dimensiones y se identifica la necesidad de crear una dimensión nueva, implícita en la selección de los vídeos, recursos, no contemplada en la versión previa.

1.ª validación por expertos y expertas en el área

Se crea una dinámica en pequeños grupos (4-5 personas, 14/03/2023). Se le pide a cada grupo determinar cuáles dimensiones e indicadores considera oportunos para seleccionar y, posteriormente, analizar los vídeos expuestos (cumpliendo las características descritas en el apartado anterior). En esta validación participaron 30 personas expertas del área de Didáctica de la Matemática, vinculadas con la investigación y la enseñanza en la etapa de Educación Infantil (descritas como el segundo grupo de interés del apartado anterior).

Tras la creación de la tabla en cada grupo y su discusión, se observa que la mayoría de los equipos hicieron aportes referidos a: 1) selección de los vídeos y 2) análisis de estos (Anexos 1-Figuras de la 3 a la 8 y Anexo 2). Por tanto, se incorporan las aportaciones atendiendo a esta diferenciación.

1. Selección de vídeos: se ve la idoneidad de las dimensiones (rol docente, respuesta alumnado y relaciones matemáticas).

2. Análisis de vídeos: se incorpora la dimensión “Recursos”, lo cual da lugar a la configuración R4:

• Rol docente: qué función tiene el/la docente en el aula.

• Respuesta del alumnado en la tarea: cómo actúa el alumnado.

• Relaciones matemáticas: analizar el tipo de matemática.

• Recursos, gestión y uso de recursos-materiales humanos.

Propuesta de mejora de los instrumentos de selección y de análisis de los vídeos tras la primera validación del grupo de personas expertas.

A partir de la mejora indicada, se consideran cuatro dimensiones para la selección y análisis de vídeos (Figura 3):

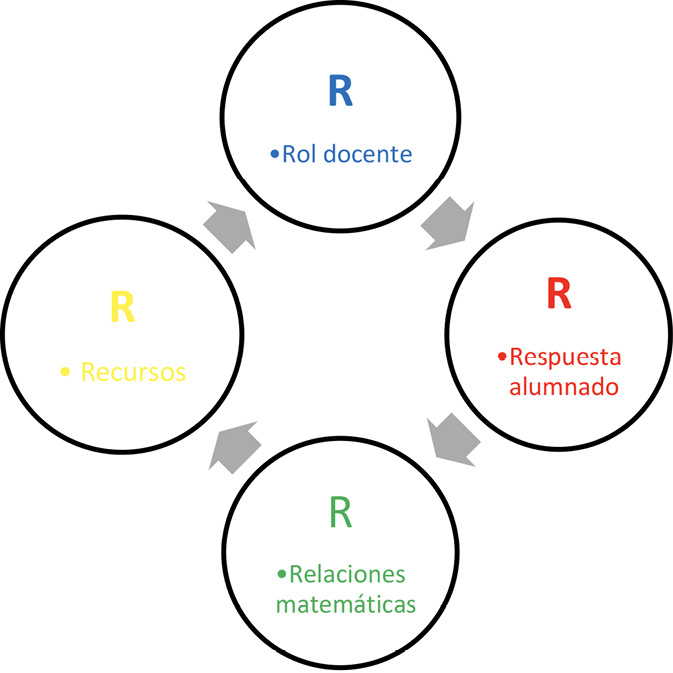
Figura 3. Dimensiones de selección y análisis

Nota: fuente propia de la investigación.

• Rol docente:

- Si el tipo de comunicación es bidireccional (si se fomenta el diálogo) o unidireccional (imperativo, expositivo).

- ¿Cómo fomenta el desarrollo matemático?

- ¿Qué tipo de preguntas realiza?

• Respuesta del alumnado en la tarea.

- Tipo de participación en su aprendizaje (activo/pasivo).

• Relaciones matemáticas en la realización de la actividad:

- Contenidos y procesos matemáticos que emergen.

- Conexiones con otras áreas de conocimiento.

- Establecimiento del ciclo C-P-A.

- Uso del error como oportunidad de aprendizaje.

• Recursos.

- Gestión y uso de materiales físicos.

- Disposición del profesorado presente en el aula y su función.

- Agrupaciones del alumnado y su “objetivo”.

Tras estos dos contrastes, se procede a crear la versión piloto completa de la rúbrica, atendiendo a las dimensiones, subdimensiones, indicadores y definición de la graduación para cada ítem. En total, el cuestionario consta de 4 dimensiones, 16 subdimensiones y un total de 28 ítems:

• Rol docente:

- Tipo de comunicación docente-discente. Marco de referencia: Jakobson (1960). 4 ítems.

- Fomento del pensamiento matemático. 1 ítem.

- Tipo de preguntas. Marco de referencia: modelo de indagación. 5 ítems.

- Uso del error como recurso: 1 ítem.

- Objetivo docente: claridad. 1 ítem.

• Respuesta del alumnado:

- Tipo de participación. 1 ítem.

- Tipo de actividad. 1 ítem.

• Relaciones matemáticas:

- Contenidos y procesos matemáticos. Marco de referencia: NCTM (2000). 1 ítem.

- Conexiones con otras áreas. Marco de referencia: (Ministerio de Educación y Formación Profesional, 2022). 1 ítem.

- Establecimiento del ciclo CPA. Marco de referencia: (Bruner, 1963, citado en Guilar, 2009), 3 ítems.

- Planteamiento de la actividad. 1 ítem.

- Materiales físicos. 1 ítem.

• Recursos:

- Pertinencia del uso de materiales.
1 ítem.

- Disposición del profesorado. 1 ítem.

- Tipos de agrupaciones del alumnado: 3 ítems.

- Sentido del tipo de agrupaciones: 2 ítems.

2.ª validación por personas expertas en el área del conocimiento

En esta fase se envía la rúbrica a seis personas expertas del área, para que puedan valorar la claridad, pertinencia y relevancia de los indicadores, así como la graduación, determinada por medio de una escala Likert 1-4, donde los valores de esta muestra un nivel muy bajo, bajo, alto o muy alto de cada uno de parámetros a evaluar (1, 2, 3 y 4, respectivamente). En la Tabla 1 se presentan las valoraciones medias obtenidas.

Tabla 1. Valoración media de las personas expertas

Valoración media	Claridad (C)	Pertinencia (P)	Relevancia (R)
Rol docente	3.2	3.8	3.7
Respuesta	3.3	3.7	3.7
Relaciones	2.8	3.8	3.8
Recursos	3.7	3.4	3.6
TOTAL	3.2	3.7	3.7

Nota: fuente propia de la investigación.

En general, la valoración de la rúbrica en todas sus dimensiones es positiva; aun así, se analiza cada uno de los ítems (Tabla 2).

Tabla 2. Puntuación media de cada ítem

Dimensión	Ítem	C	P	R	Dimensión	Ítem	C	P	R
Rol docente	n.1	3.1	4	3.3	Relaciones Matemáticas	n.15	3	4	3.6
	n.2	3.1	4	4		n.16	2.8	4	4
	n.3	3.1	4	4		n.17	2.6	4	4
	n.4	3	3.6	3.8		n.18	2.8	4	4
	n.5	2.3	3.3	3.3		n.19	2.6	4	4
	n.6	3.6	4	4		n.20	3.3	4	4
	n.7	3.8	4	4		n.21	2.6	2.6	3.5
	n.8	3.5	4	4	Recursos	n.22	3.5	3.8	3.8
	n.9	3.6	3.6	3.5		n.23	3.5	3.5	4
	n.10	3	4	4		n.24	3.8	3.3	3.5
	n.11	3	4	4		n.25	3.8	3.3	3.5
	n.12	3	3.6	3.3		n.26	3.8	3.3	3.5
Respuesta Alumnado	n.13	3.3	4	4		n.27	4	3.3	3.6
	n.14	3.3	3.5	3.5		n.28	4	3.3	3.5

Nota: fuente propia de la investigación (C: claridad, P: pertinencia, R: relevancia).

Tras el análisis detallado por medio de la triangulación del equipo investigador de las valoraciones realizadas sobre la claridad, se introducen los siguientes cambios en la rúbrica (Tabla 3):

Tabla 3. Cambios introducidos en la rúbrica R4 en ítems con valoración negativa

Ítem	Motivo	Mejora realizada	Tipología de modificación
n. 1-4	Unificar la redacción explicativa de los ítems	Se unifica	De carácter gramatical, mayor especificidad en la definición
n. 5	Se sugiere suprimir “básicos” del tipo de acciones, ejemplos, …	Se suprime “básicos”	De carácter gramatical
n.15-16-17	Substitución de nombre de indicadores, explicitación mayor	Se añade “representación” al nombre de cada ítem	De carácter gramatical, mayor especificidad en la definición
n.21	Se considera ya evaluado en otras dimensiones	Se suprime	Redundancia de ítem
n. 24-25-26	Substitución de nombre de indicadores, explicitación mayor	Se añade “agrupación” al nombre de cada ítem	De carácter gramatical, mayor especificidad en la definición

Nota: fuente propia de la investigación.

Igualmente, se analizó la valoración media recibida en la graduación definida (Tabla 4), obteniéndose:

Tabla 4. Valoraciones medias

Dimensión	Claridad	Pertinencia	Relevancia
Rol docente	2.9	3.8	3.8
Respuesta	2.8	3.5	3.5
Relaciones	2.5	3.5	3.8
Recursos	3.3	3.5	3.4
TOTAL	2.9	3.6	3.7

Nota: fuente propia de la investigación.

En este caso, se analizaron los comentarios y sugerencias de mejora de cada evaluador o evaluadora externa (Tabla 5), incorporándose los siguientes cambios:

Tabla 5. Mejoras incorporadas

Ítems con valoración negativa	Motivo	Mejora realizada	Tipología de modificación
n.1-4	Sustitución verbo en la graduación (tener->presentar)	Se acepta	De carácter gramatical, mayor especificidad en la definición
n.5	Se sugiere suprimir “básicos” de la graduación de los ítems	Se suprime “básicos”	De carácter gramatical
n.6, 13, 14	Se sugiere cuantificar el número de contenidos	Se gradúa cuantificando	Cambio de escala cualitativa a cuantitativa
n.7-8-9-10	Reubicación de “parcialmente” en la graduación de segundo nivel	Se reescribe el segundo nivel	De carácter gramatical, mayor especificidad en la definición
n.15-16-17	Subsanación de la graduación de tercer nivel, añadir “no”	Se reescribe el tercer nivel	Error tipográfico
n.28	Subsanación de la graduación de primer nivel, suprimir “idóneo”	Se reemplaza “idóneo” por “pertinente”	De carácter gramatical, mayor especificidad en la definición

Nota: fuente propia de la investigación.

Fase 4. Modificaciones y estructura final de la Rúbrica R4

Finalmente, se presenta la estructura final de la rúbrica R4, conformada por cuatro dimensiones, 16 subdimensiones y un total de 27 ítems (Anexo 3):

• Rol docente:

- Tipo de comunicación docente-discente: Jakobson (1960). 4 ítems.

- Fomento del pensamiento matemático. 1 ítem.

- Tipo de preguntas: modelo de indagación. 5 ítems.

- Uso del error como recurso: 1 ítem.

- Objetivo docente: claridad. 1 ítem.

• Respuesta del alumnado en la tarea:

- Tipo de participación. 1 ítem.

- Tipo de actividad. 1 ítem.

• Relaciones matemáticas:

- Contenidos y procesos matemáticos: NCTM (2000). 1 ítem.

- Conexiones con otras áreas (Ministerio de Educación y Formación Profesional, 2022). 1 ítem.

- Establecimiento del ciclo CPA (Bruner, 1963, citado en Guilar, 2009).
3 ítems.

- Planteamiento de la actividad. 1 ítem.

• Recursos humanos y materiales:

- Pertinencia del uso de materiales.
1 ítem.

- Disposición del profesorado. 1 ítem

- Tipos de agrupaciones del alumnado: 3 ítems.

- Sentido del tipo de agrupaciones: 2 ítems.

Conclusiones

En las asignaturas de Didáctica de la Matemática de los títulos de Grado de Magisterio, las prácticas docentes impulsadas en las últimas décadas a partir de la implementación del Espacio Europeo de Educación Superior, y basadas en una participación más activa del profesorado en formación inicial, se han encontrado con el obstáculo de grupos de aula numerosos (de un promedio de 60 estudiantes o incluso más en el caso de las universidades españolas), lo cual dificulta la superación de la clase magistral. Por otro lado, como se ha señalado, diversos estudios plantean la necesidad de vincular más la educación matemática a los contextos de experiencia y no tanto a la discusión de rutinas por medio de la diversificación de metodologías de aula (Planas, 2006).

Desde esta perspectiva, en este artículo se ha descrito el proceso de creación y validación de la rúbrica R4, al mostrar las distintas fases, con sus contrastes y mejoras introducidas para la selección y análisis de vídeos, como instrumento para ayudar a vincular más y mejor la educación matemática con los contextos de experiencia. Como se ha señalado, esta herramienta permite, por un lado, seleccionar vídeos docentes de aula y, por otro, observarlos de modo sistemático para promover el desarrollo profesional, a partir de cuatro dimensiones: 1) rol docente, sobre la función que tiene la persona docente en el aula; 2) respuesta del alumnado infantil en la tarea, sobre su actuación; 3) relaciones matemáticas, sobre el tipo de matemática y 4) recursos, sobre la gestión y uso de recursos-materiales humanos.

Atendiendo a un objetivo formativo claramente determinado por la persona docente, tras planificar de forma adecuada la secuencia de actividades sobre el visionado del vídeo (Bautista García-Vera, 2013), se puede seleccionar unos u varios vídeos (con características parcialmente comunes), para, luego, establecer una discusión grupal a partir del uso de la herramienta R4, la cual proporciona evidencias para que dicha dinámica dé lugar a la reflexión de grupo (Coles, 2019) y, por ende, fomente el desarrollo de la competencia noticing (Joglar et al., 2021; Llinares, 2007).

Este aspecto, aunque no se contempla en este artículo, determina una clara línea de actuación con el profesorado en formación inicial de educación infantil, por medio de la siguiente secuencia de actividades: 1) selección del área matemática; 2) visionado grupal; 3) análisis individual, haciendo uso de R4; 4) puesta en común en pequeños grupos; 5) discusión y consenso en grupo-clase; y 6) finalmente, reflexión individual.

Como principales limitaciones, que a su vez sirven para determinar futuras líneas de investigación, cabe señalar que dicha herramienta (la de selección) no se ha puesto en marcha en la selección de vídeos con el profesorado responsable de la formación inicial del estudiantado de educación infantil, por lo que en futuros análisis será necesario analizar qué cambios se producen en esta fase gracias a la rúbrica R4. Igualmente, no se ha probado con vídeos en la formación inicial de profesorado, lo cual lleva a plantear como futuras líneas de investigación qué tipo de reflexiones hace este colectivo sobre las distintas prácticas docentes matemáticas, gracias a dicha herramienta, entre otros.

Financiamiento

Trabajo parcialmente financiado por el Grupo de investigación GIU21/031 de la Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) y por el Proyecto de investigación PID2021-122326OB-I00, España.

Conflicto de intereses

Las personas autoras declaran no tener algún conflicto de interés.

Declaración de la contribución de las personas autoras

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo.

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: A. B. 33.3 %, M. S. 33.3 % y Á. A. 33.3 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor o la autora correspondiente [AB], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://doi.org/10.5281/zenodo.8297509

Referencias

Alonso-Sainz, T. (2019). ¿Qué estudiantes de Magisterio queremos en España? Expectativas de los centros universitarios españoles mostradas en los perfiles de ingreso y egreso. En J. Manso, La formación inicial del profesorado en España. Análisis de los planes de estudios tras una década de su implementación (pp. 42-58). Ministerio de Educación y Formación Profesional. https://sede.educacion.gob.es/publiventa/d/23106/19/00

Alsina, Á. (2020). La Matemática y su didáctica en la formación de maestros de Educación Infantil en España: crónica de una ausencia anunciada. La Gaceta de la RSME, 23(2), 373-387.

Azer, S. A., AlGrain, H. A., AlKhelaif, R. A. y AlEshaiwi, S. M. (2013). Evaluation of the Educational Value of YouTube Videos about Physical Examination of the Cardiovascular and Respiratory Systems. Journal of Medical Internet Research, 15(11), e241, 1-14. https://doi.org/10.2196/jmir.2728

Bautista García-Vera, A. (2013). Funciones del video en la formación del profesorado para una educación intercultural. Educatio Siglo XXI, 31(1), 255-268.

Burgos, M., Beltrán-Pellicer, P. y Godino, J. D. (2020). La cuestión de la idoneidad de los videos educativos de matemáticas: una experiencia de análisis con futuros maestros de educación primaria | The issue of didactical suitability in mathematics educational videos: experience of analysis with prospective primary school teachers. Revista Española de Pedagogía, 78 (275), 27-49. https://doi.org/10.22550/REP78-1-2020-07

Callejo, M. L., Valls, J. y Llinares, S. (2007). Interacción y análisis de la enseñanza. Aspectos claves en la construcción del conocimiento profesional. Investigación en la Escuela, 61, 5-21.

Coles, A. (2019). Facilitating the use of video with teachers of mathematics: learning from staying with the detail. International Journal of STEM Education, 6(5), 1-13. https://doi.org/10.1186/s40594-018-0155-y

Esteley, C., Villarreal, M., Mina, M. y Coirini, A. (2021). Uso de videos en la formación inicial de profesores de matemática como recurso para observar clases. Revista Científica EFI-DGES, 7(12), 65-89.

García Matamoros, M. A. (2014). Uso Instruccional del video didáctico. Revista de Investigación, 38(81), 43-67.

Guardia González, S. (1990). Efectos del uso del video en la formación del profesorado de EGB. Revista Complutense de Educación, 1(3), 373-399.

Jakobson, R. (1960). Closing statement: lingüistics and poetics. En T. A. Sebeok (Ed.), Style in Language (pp. 350-377). Jonsons Wiley & Sons, Inc.

Joglar Prieto, N., Belmonte Gómez, J. M., Liñán García, M. M., Muñoz Catalán, M. C., Pizarro Contreras, R. N., Ramírez García, M. y Méndez Coca, M. (2021). El papel de una tarea formativa sobre el número en el desarrollo de la competencia noticing del futuro maestro de Educación Infantil. En GIDIMAT (Eds.), Ideas para la Educación Matemática (pp. 183-203). Universidad de Alicante.

Ministerio de Educación y Ciencia. (2007). ORDEN ECI/3854/2007, de 27 de diciembre, por la que se establecen los requisitos para la verificación de los títulos universitarios oficiales que habiliten para el ejercicio de la profesión de Maestro en Educación Infantil. https://boe.es/boe/dias/2007/12/29/pdfs/A53735-53738.pdf

National Council of Teachers of Mathematics [NCTM] (2000). Principles and standards for school mathematics. Reston: National Council of Teachers of Mathematics (Trad. Castellana, Principios y estándares para la educación matemática. Sociedad Andaluza de Educación Matemática Thales, 2003).

Planas, N. (2006). Modelo de análisis de videos para el estudio de procesos de construcción de conocimiento matemático. Educación Matemática, 18(1), 37-72.

Portugal, K. O., Arruda, S. D. M. y Passos, M. M. (2018). Free-choice teaching: how YouTube presents a new kind of teacher. Revista Electrónica de Enseñanza de las Ciencias, 17(1), 183-199.

Ramírez, A. (2010). Youtube y el desarrollo de la competencia matemática. Resultados de una investigación cuasi-experimental. Contextos Educativos, 13, 123-138. https://doi.org/10.18172/con.630

Rosales López, C. (2014). Utilización activa del video en la formación inicial de educadores. Tendencias Pedagógicas, 24, 387-400.https://doi.org/10.15366/tp2014.24.024

Santagata, R. y Guarino, J. (2011). Using video to teach future teachers to learn from teaching. ZDM Mathematics Education, 43, 133-145. https://doi.org/10.1007/s11858-010-0292-3

Santos, J. A. (2018). Valoración de video tutoriales de matemáticas disponibles en Internet. Nuevos instrumentos para el análisis de los procesos educativos (Tesis doctoral). Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional.

Studying and improving Mathematics instruction in secondary schools in Spain study group [grupo de estudio SiMiS] (2021). POEMat.es: Pauta de observación de la enseñanza de matemáticas en educación secundaria en España. AIEM-Avances de Investigación en Educación Matemática, 20, 89-103.https://doi.org/10.35763/aiem20.4004

Vásquez Ortiz, C. A., Alsina, Á., Pincheira Hauck, N. G., Gea Serrano, M. M. y Chandia Muñoz, E. (2020). Construcción y validación de un instrumento de observación de clases de probabilidad. Enseñanza de las Ciencias, 38(2), 25-43. https://doi.org/10.5565/rev/ensciencias.2820

Charalambous, C. Y. y Praetorius, A. K. (2018). Studying mathematics instruction through different lenses: Setting the ground for understanding instructional quality more comprehensively. ZDM Mathematics Education, 50(3), 355-366. https://doi.org/10.1007/s11858-018-0914-8

Ministerio de Educación y Formación Profesional (2022). Real decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria [LOMLOE]. https://www.boe.es/buscar/pdf/2022/BOE-A-2022-3296-consolidado.pdf

Guilar, M. E. (2009). Las ideas de Bruner: “de la revolución cognitiva” a la “revolución cultural”. Educere, 13(44), 235-241. http://erevistas.saber.ula.ve/index.php/educere/article/view/13289

Anexo 1: primera validación de personas expertas por grupos

Figura 3. Validación de expertos y expertas Grupo G4

Nota: fuente propia de la investigación.

Figura 4. Validación de expertos y expertas Grupo G3

Nota: fuente propia de la investigación.

Figura 5. Validación de expertos y expertas Grupo G5

Nota: fuente propia de la investigación.

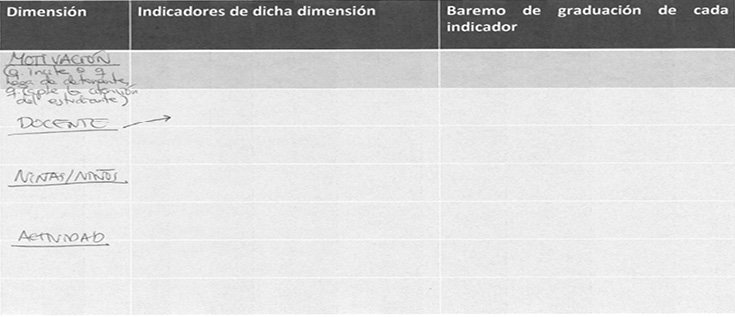
Figura 6. Validación de expertos y expertas Grupo G2

Nota: fuente propia de la investigación.

Figura 7. Validación de expertos y expertas Grupo G1

Nota: fuente propia de la investigación.

Figura 8. Validación de expertos y expertas Grupo G6

Nota: fuente propia de la investigación.

Anexo 2. Resumen de la validación por grupos de personas expertas

Grupos/ Dimensiones*	D1	D2	D3	D4	D5	D6
G1	Conocimientos matemáticos • Contenidos • Procesos	Tipo de tarea • Contexto real simulado	Tipo de gestión • Indagación • Explicación	Herramienta de evaluación • Preguntas • Prueba escrita	Duración del vídeo • Menos de 2 minutos • 2 minutos • Más de 2 minutos	Aspectos de formato • Ubicación de la cámara • ruido • imagen

Grupos/ Dimensiones*	D1	D2	D3	D4
G2	Motivación • que incite o que haga de detonante, que capte la atención del alumnado)	Docente	Niñas/niños	Actividad

Grupos/ Dimensiones*	D1	D2	D3	D4	D5	D6	D7	D8
G3	Comunicación (lenguaje) • Nivel adaptado (edad) • Contenido • Interacción (p->a, a->p, a<->a): o Unidireccional o ¿tipo de reflexión? o ¿Atención? ¿respuestas? o ¿a través de preguntas?	Enseñanza estilo • Instrucción directa • ¿reto?	Gestión aula • ¿llega a todos? • ¿situación real/ cotidiana/ contextualizada? • ¿ejemplos? • ¿cómo corrige?	Espacio • Disposición de los niños • Posición del maestro	Tiempo • ¿sesión completa? I-P-E • ¿se ve toda la sesión de clase?	Cuestiones técnicas: • ¿se escucha bien? • ¿se ven las interacciones completas? • ¿transcripción del lenguaje niño->adulto?	Fases: • Introducción • … • Evaluación	Contenido matemático • ¿qué ha pasado?

Grupos/ Dimensiones*	D1	D2	D3	D4	D5	D6
G4	Objetivos de aprendizaje de maestra • no se ven • sistema decimal • id. regletas • equilibrio térmico	Objetivos de los niños	Evidencia de aprendizaje matemático	Lenguaje (tipo de interacciones): • No • Guiado (total) • Real	Registros: • Uso y conversiones (graduar) • Materiales (¿cómo?)	Organización de aula

Grupos/ Dimensiones*	D1	D2
G5	Docente: · unidireccional	Material

Grupos/ Dimensiones*	D1	D2	D3	D4	D5
G6	Fases de la puesta en práctica de la dinámica (tipo de actuación) • presenta • desarrollo • cierre (síntesis)	andamios • feedback • preguntas • refuerzo • etc	Diversas dinámicas • trabajo grupal • trabajo individual trabajo en pequeño grupo (parejas)	Gestión de un error	Participación

*La numeración no tiene ningún significado, salvo el orden de escritura en la hoja facilitada, pero el color azul hace referencia a dimensiones de análisis de los vídeos y el color negro a la selección de estos.

Anexo 3. Versión definitiva de la Rúbrica R4

Dimensión	Subdimensiones	Items asociados	Sí se cumple	Se cumple parcialmente	No se cumple
Rol docente	Tipo de comunicación: funcionalidad (Jakobson, 1960)	Función referencial: busca realizar una* descripción de una situación;	La comunicación presenta función referencial	La comunicación presenta parcialmente función referencial	La comunicación no presenta función referencial
		Función emotiva: busca enfatizar sentimientos de la persona emisora;	La comunicación presenta función emotiva	La comunicación presenta parcialmente función emotiva	La comunicación no presenta función emotiva
		Función conativa, busca una respuesta en la persona receptora;	La comunicación presenta función conativa	La comunicación presenta parcialmente función conativa	La comunicación no presenta función conativa
		Función fática, busca establecer un canal de interlocución	La comunicación presenta función fática	La comunicación presenta parcialmente función fática	La comunicación no presenta función fática
	Fomento del pensamiento matemático	Por medio de preguntas, acciones, instrucciones directas y/o ejemplos	Fomenta el desarrollo matemático por medio de preguntas, de acciones, instrucciones y/o ejemplos, que son adecuados.	Fomenta el desarrollo matemático por medio de preguntas, de acciones, instrucciones y/o ejemplos, pero poco claros.	Fomenta el desarrollo matemático por medio de preguntas, de acciones, instrucciones y/o ejemplos, con omisiones y/o errores.
	En caso de realizar preguntas, valoración de su objetivo (modelo de indagación)	Introductorias (preguntas dirigidas a ver si los niños y las niñas han entendido la tarea, identifican los aspectos relevantes, …)	Conecta al menos dos contenidos matemáticos con las preguntas introductorias de forma adecuada.	Conecta un contenido matemáticos con las preguntas introductorias de forma adecuada.	No conecta ningún contenido matemáticos con las preguntas introductorias de forma adecuada.
		Argumentación (preguntas dirigidas a provocar algún tipo de justificación)	Formula preguntas dirigidas a elaborar argumentos matemáticos	Formula preguntas dirigidas a elaborar parcialmente argumentos matemáticos	No formula preguntas dirigidas a elaborar argumentos matemáticos
		Indagación (preguntas dirigidas a: observar, explorar,…)	Plantea preguntas adecuadas que promuevan la observación, exploración…	Plantea preguntas dirigidas a promover parcialmente la observación, exploración…	No plantea preguntas dirigidas a la observación, exploración…
		Modelización (preguntas dirigidas a provocar algún tipo de descripción de un modelo matemático)	Hace preguntas adecuadas para que los niños o niñas describan modelos matemáticos	Hacen preguntas que fomentan parcialmente la descripción de modelos matemáticos	No hace preguntas que fomenten la descripción de modelos matemáticos
		Concreción (preguntas dirigidas a entender y resolver el problema, haciendo uso de representaciones físicas o gráficas)	Formula preguntas matemáticas adecuadas para entender y/o resolver el problema correctamente	Formula preguntas matemáticas poco adecuadas para entender y/o resolver el problema correctamente	No formula preguntas matemáticas adecuadas para entender y/o resolver el problema
	Uso del error como oportunidad de aprendizaje	Si aparece el error, se usa como recurso o como una oportunidad de enseñanza	Detecta los errores matemáticos de forma competente, aprovechándolos como un recurso u oportunidad de enseñanza	Detecta los errores matemáticos, aprovechándolos parcialmente como recurso u oportunidad de enseñanza	No detecta los errores matemáticos o no los usa como una oportunidad de aprendizaje
	Objetivo docente	Claridad en el objetivo docente	Las intenciones del docente se observan claramente y de forma explícita a lo largo de todo el proceso	Las intenciones del docente se intuyen y son confusas a lo largo del proceso	No están claras las intenciones del docente a lo largo del proceso

Dimensión	Subdimensiones	Items asociados	Sí se cumple	Se cumple parcialmente	No se cumple
Respuesta del alumnado en la tarea (se analiza en relación grupo-aula)	Tipo de participación en su aprendizaje	Pasiva/Activa	Participa activamente a lo largo de todo el desarrollo de la actividad	Participa activamente en alguna parte de la actividad	No participa a lo largo del desarrollo de la actividad
	Tipo de actividad del alumnado	Relacionada con el objetivo docente	Conecta los conocimientos matemáticos con las intenciones del docente	Conecta parcialmente los conocimientos matemáticos con las intenciones del docente	No conecta los conocimientos matemáticos con las intenciones del docente

* Los textos en rojo de la rúbrica hacen alusión a los cambios introducidos tras la revisión de las modificaciones sugeridas por las personas expertas en la 2.ª validación del instrumento.

Dimensión	Subdimensiones	Items asociados	Sí se cumple	Se cumple parcialmente	No se cumple
Relaciones matemáticas	Contenidos y procesos matemáticos que emergen (NCTM)	“Contenidos y procedimientos trabajados”	El desarrollo de la actividad permite trabajar al menos dos contenidos y/o procesos	El desarrollo de la actividad permite trabajar un contenido y/o proceso	El desarrollo de la actividad no permite trabajar contenidos ni procesos
	Conexiones con otras áreas de conocimiento	“Conexiones con otras áreas”	Conecta todos los contenidos matemáticos con otras áreas de conocimiento.	Conecta alguno de los contenidos matemáticos con otras áreas de conocimiento.	No conecta los contenidos matemáticos con otras áreas de conocimiento.
	Establecimiento del ciclo C-P-A	Representaciones concretas	El desarrollo de la actividad permite representar situaciones matemáticas utilizando modelos físicos de forma correcta	El desarrollo de la actividad permite representar alguna situación matemática utilizando modelos físicos de forma parcialmente correcta	El desarrollo de la actividad no permite representar situaciones matemáticas utilizando modelos físicos
		Representaciones pictóricas	El desarrollo de la actividad permite representar situaciones matemáticas utilizando representaciones pictóricas de forma correcta	El desarrollo de la actividad permite representar alguna situación matemática utilizando representaciones pictóricas de forma parcialmente correcta	El desarrollo de la actividad no permite utilizar representaciones pictóricas para representar situaciones matemáticas
		Representaciones abstractas o simbólicas	El desarrollo de la actividad permite representar situaciones matemáticas usando lenguaje matemático de forma correcta	El desarrollo de la actividad permite representar parcialmente situaciones matemáticas usando lenguaje matemático	El desarrollo de la actividad no permite representar situaciones matemáticas usando lenguaje matemático
	Planteamiento de la actividad	La actividad permite distintos modos de resolución	El planteamiento de la actividad invita a crear distintos caminos y modos de resolución	El planteamiento de la actividad invita parcialmente a crear distintos caminos y modos de resolución	El planteamiento de la actividad no permite distintos caminos y modos de resolución

Dimensión	Subdimensiones	Items asociados	Sí se cumple	Se cumple parcialmente	No se cumple
Recursos humanos y materiales	Pertinencia del uso de materiales	Alineación con el objetivo docente	Utilizan materiales adecuados para el desarrollo de la actividad	Alguno de los materiales es adecuado para el desarrollo de alguna parte de la actividad	Los materiales son inadecuados para el desarrollo de la actividad
	Disposición del profesorado presente en el aula y su función	Participación de todo el profesorado del aula en la actividad (de modo no observacional ni asistencial)	El rol de todos los docentes que intervienen es de guía y adecuado en toda la actividad	El rol de alguno de los docentes que interviene es de observación y no interactúa con el alumnado como guía	Ningún docente guía la actividad o la metodología es puramente conductista
	Tipos de agrupaciones “físicas” del alumnado	Agrupación individual	Se promueve actividad individual a lo largo de toda la tarea	Se promueve actividad individual en alguna parte de la tarea	No se promueve actividad individual para resolver la tarea en ningún momento
		Agrupación en parejas o pequeños grupos	Se promueve actividad en pequeños-grupos a lo largo de toda la tarea	Se promueve actividad en pequeños-grupos en alguna parte de la tarea	No se promueve actividad en pequeños-grupos en ningún momento de la tarea
		Agrupación en gran grupo (clase)	Se promueve actividad en grupo-clase a lo largo de toda la tarea	Se promueve actividad en grupo-clase en alguna parte de la tarea	No se promueve actividad en grupo-clase en ningún momento de la tarea
	Sentido del “objetivo” de las agrupaciones	Fomenta el aprendizaje del alumnado	El tipo de agrupamiento permite generar aprendizajes matemáticos adecuados	El tipo de agrupamiento permite generar algún aprendizaje matemático	El tipo de agrupamiento no permite generar ningún aprendizaje matemático
		Relación con la actividad	El tipo de agrupamiento es pertinente para el desarrollo de la tarea	El tipo de agrupamiento es parcialmente pertinente para la resolución de la tarea	El tipo de agrupamiento no es pertinente para el desarrollo de la tarea

* Los textos en rojo de la rúbrica hacen alusión a los cambios introducidos tras la revisión de las modificaciones sugeridas por las personas expertas en la 2.ª validación del instrumento.

---

1. 1* Corresponding author

   Ainhoa Berciano, ainhoa.berciano@ehu.eus, https://orcid.org/0000-0001-7399-4745

   María Salgado, maria.salgado@usc.es, https://orcid.org/0000-0002-0309-241X

   Ángel Alsina, angel.alsina@udg.edu, https://orcid.org/0000-0001-8506-1838

   Departamento de Didáctica de la Matemática, Ciencias Experimentales y Sociales, Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU), Leioa, España.

1. 2 Departamento de Didácticas Aplicadas, Universidad de Santiago de Compostela, Santiago de Compostela, España.

1. 3 Departamento de Didácticas Específicas, Facultad de Educación y Psicología, Universidad de Girona, Girona, España.