
Revista UNICIENCIA
Uniciencia Vol. 38(1), January-December, 2024
E-ISSN: 2215-3470
DOI: https://dx.doi.org/10.15359/ru.38-1.34
Adaptation and Validation of a Scale of Self-Regulation of Learning in Mathematical Problem Solving
Adaptación y validación de una escala de autorregulación del aprendizaje en resolución de problemas matemáticos
Adaptação e validação de uma escala de autorregulação da aprendizagem na resolução de problemas matemáticos
Josune Landa1, Ainhoa Berciano1, José M. Marbán2*
Received: Sep/12/2023 • Accepted: Apr/23/2024 • Published: Nov/30/2024
Mathematical learning plays a fundamental role in the integral development of students at all ages and educational levels, as it provides them with the necessary tools to develop critical thinking and creativity and, in this way, solve problems in everyday life. The United Nations Educational, Scientific and Cultural Organization (UNESCO, 2016) recognizes the importance of mathematical competence, and its promotion is included as part of Sustainable Development Goal 4.4, whose purpose is to ensure that students acquire knowledge and skills in mathematics, which implies ensuring inclusive and quality education for everybody.
In this context, initial and continuous training for the development of mathematical competence in teachers is essential, since they are responsible for both transmitting knowledge and strengthening students’ ability to raise questions, explore different problem-solving strategies, analyze errors, and justify their ideas (García, 2019; Muñoz-Fernandez et al., 2019; Schoenfeld, 2018; Lachapell, 2017; Alguacil et al., 2016).
However, despite the presence, importance, and need for mathematics in all areas of life, research such as TEDS-M (2012) (Teacher Education and Development Study in Mathematics) shows, in the case of Spain, overall scores below the OECD (Organization for Economic Cooperation and Development) average in mathematical and mathematical pedagogical knowledge by teachers in initial training (INEE, 2013). More recent studies support this finding and provide further evidence that the mathematical and mathematical pedagogical knowledge of preservice teachers remain an area of concern (Segarra and Julià, 2021; Nortes and Nortes, 2018). The lack of teacher training in mathematics is one of the factors that would explain, in turn, the low results obtained in international assessments, such as PISA (2018) (Program for International Student Assessment) and TIMSS (2019) (Trends in International Mathematics and Science Study), of student performance in mathematics; these results are also below the international average (Gutiérrez-Gutiérrez, et al., 2016; Döhrmann, Kaiser and Blömeke, 2014). The improvement of teacher education in mathematics must integrate the positive development of mathematical knowledge with aspects of the affective domain. Thus, in TEDS-M (2012), an increase in mathematical knowledge reduces the belief that this discipline is reduced to a set of rules. In this sense, the study by Marbán et al. (2021) highlights the fact that a greater mastery of mathematical concepts in initial teacher training reduces anxiety and strengthens the positive self-concept of mathematics.
In this context, several investigations in mathematics education point to a set of underlying factors (motivational, affective, and cognitive) that affect academic performance. Thus, there are negative attitudes and beliefs toward mathematics—particularly toward problem-solving—as well as emotions and feelings that translate into anxiety, insecurity, frustration and distress (Zamora, 2020; Chen and Lo, 2019; Luttenberger, Wimmer and Paechter, 2018; Nortes Martínez-Artero and Nortes Checa, 2017; Araya and Moreira-Mora, 2016; Caballero, Cárdenas and Gordillo, 2016; Boaler, 2016)
These factors that influence mathematics teaching and learning are also transmitted through instruction (Karunakaran, 2020; Mizala et al., 2015; Sakiz, Pape y Hoy, 2012). In this sense, sociocognitive theories point out that a key element for students’ academic success is their capacity to self-regulate their own learning (White and DiBenedetto, 2018; Dignath and Büttner, 2018; Hadwin, et al., 2018; Bembenutty et al., 2015; Panadero and Alonso-Tapia, 2014; Zimmerman, 2013; Zimmerman and Kitsantas, 2014; Zimmerman and Moylan, 2009). Similarly, motivational variables related to the self-regulation of learning are increasingly highlighted in the literature, thus consolidating themselves as crucial topics for academic success (Nájera et al., 2020; Suárez et al., 2018).
At this point, it should be noted that, although very consistent work has established self-regulation as a potential predictor of academic performance in mathematics (Harding et al., 2019; Cleary et al., 2017), studies on self-regulation in mathematical problem-solving contexts remain scarce.
From this perspective and following the literature review carried out in this field, the need to construct a scale that measures the level of self-regulation in mathematical problem-solving contexts has been identified. The Likert scale, designed by Fernández-Gago and Marbán (2022) for secondary school students, is taken as a starting point. After the scale was adapted and validated for university students, it was able to fill the gap detected.
There are several theories on self-regulation of learning that contribute to the understanding of this construct and the promotion of its development (Panadero and Alonso-Tapia, 2014). However, some of these theories (operant, phenomenological, information processing, volitional and Vygotskian) focus only on the preconditions or processes necessary to achieve self-regulation but do not delve into how self-regulation is acquired as an internal process or how it manifests itself in the strategies employed. These theories therefore offer only a partial perspective of self-regulation. In a complementary manner, the sociocognitive theory and the constructivist theory address both the cognitive and social aspects of self-regulation, providing a more comprehensive understanding of the process.
It is important to recognize that no single theory can fully explain the acquisition of self-regulation. However, by combining different theoretical approaches, a comprehensive framework can be constructed that encompasses both the internal and contextual aspects of self-regulated learning.
In this context, the present study is conceptualized from a sociocognitive perspective. This approach is fundamental to understanding how students regulate their own learning and achieve better academic results (Schunk and Usher, 2018). From this perspective, the self-regulation model proposed by Zimmerman (2002) is one of the most widely used models in research and guides the development of the present work. The work also uses Boekarts’ model for integrating important aspects related to affectivity and specific domains, both crucial in the learning of mathematics and, in particular, in mathematical problem-solving.
Zimmerman’s model approaches self-regulated learning in several phases, dimensions and levels. This model has three phases: (1) a forethought phase, which consists of the activation of motivational processes and beliefs and involves task analysis, planning, and setting learning objectives and goals; (2) a performance phase, which involves the performance of the task through personal control and observation strategies that lead the student to complete the planning; and (3) a self-reflection phase, which involves the student’s judgment of their performance. These phases (Figure 1) are reproduced in a cyclical way and affect each other (Zimmerman, 2002).
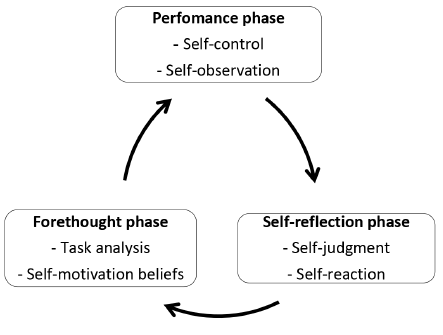
Figure 1
Phase Model and Associated Processes of Self-Regulated Learning
Note. Adapted from Zimmerman and Moylan (2009).
Another relevant aspect of Zimmerman’s model is its dimensions (motives, methods, time, behavior, the physical environment, and the social environment). These refer to what needs to be regulated in learning. Within each dimension, there are key processes that allow acting on the proper dimension and changing it, which is essential to achieve successful learning. Thus, we have motives directing students toward the goals they wish to achieve, with two important aspects in this dimension being goals and self-efficacy. The method dimension refers to how self-regulated learning occurs. Here, the key processes are the strategies and routines that each student uses to learn effectively. In the time dimension, the self-regulated learner chooses when and for how long to engage in a specific task. Time management is a key process in this dimension. The behavior dimension refers to the outcomes or levels of competence that the learner wishes to achieve. The key self-regulatory processes in this dimension include self-observation, self-judgment, and self-reaction.
In addition to these dimensions, Zimmerman also takes into account the physical and social environments. The first refers to how the physical environment is structured to facilitate self-regulated learning, while the second focuses on the interactions and relationships with others that influence the learning process.
Finally, the levels represent a progression in the development of self-regulation, from relying on external models to achieving the ability to regulate independently and adaptively. As the students progress through these levels, they become more competent and autonomous in their learning. In the first level, observation, students observe a model that shows them how to perform the task or activity. In the second level, emulation, students try to emulate what the model has done in the task, following the steps or strategies of the model in a similar way, and try to replicate it. At the third level, self-monitoring, the learners begin to have greater control over their own performance; they acquire skills and strategies to monitor and regulate their own learning process. They can evaluate their progress, identify errors, and make adjustments in their approach to study. At the fourth and final level, self-regulation, students can act autonomously and adapt to different learning contexts (Panadero and Alonso-Tapia, 2014).
Boekaerts’ model (1997), which complements the model described above in our study, states that one of the objectives of self-regulated learning is to redirect the path of well-being toward the path of learning. This idea serves as the basis for the construction of a new dimension, ethics, proposed by Marbán and Fernández-Gago (2022).
Mathematical Problem-Solving and Self-Regulated Learning
Within the field of mathematics, studies point to the capacity for self-regulation and certain motivational variables that affect it as a key element for student success in this subject. The study by Cleary and Chen (2009) in particular, examines the level of mathematics achievement together with differences in self-regulation and motivation in a sample of 880 students at an intermediate level of education. One of the most important results of this study is that the self-regulation and motivation profile was more maladaptive as the educational level increased. In addition, interest in the task was shown to be the main predictor of the use of regulation strategies by students during the learning process.
In this line, Throndsen (2011) conducted a study with the aim of examining the relationships between mathematical skills and the use of metacognitive strategies and motivational beliefs in primary school students of different levels. The analyses showed that good performance in mathematics was related not only to the use of strategies, but also to metacognitive competence, and attributions of success to effort and highly perceived self-efficacy.
Similarly, and in relation to motivational beliefs, issues such as self-efficacy, outcome expectations, interest and goals are closely related to achievement in mathematics (Segarra et al., 2021; Zamora, 2020; Usher and Pajares, 2008).
Current models of self-regulation also stress the importance of both motivational and emotional processes (Tzohar-Rozen and Kramarski, 2017; Efklides, 2011). In addition, the study conducted by Schoenfeld (1992) plays an important role, as it focusses on the students’ resources and metacognitive strategies, as well as their beliefs and affects towards this type of task.
Zimmerman’s model (2002) also takes into consideration the students’ beliefs. Likewise, this model handles phases that clearly overlap with the classic phases of problem-solving proposed by Polya (1990). These phases are as follows: (1) Understanding phase: in this phase, the student faces the problem and tries to understand it in depth. (2) Designing a plan: in this second phase, the student establishes specific goals, selects resolution strategies and develops an action plan to address the problem. (3) Carrying out the plan: in this phase, the students implement the previously designed action plan, apply the strategies, and perform the necessary calculations or steps to solve the problem. (4) Review process: once the learner finds a solution, they evaluate its validity and accuracy.
The parallelism identified between Zimmerman’s and Polya’s models shows the relevance of the phases in the process of self-regulated learning and problem-solving, providing a comprehensive framework for the present study (Callan, 2014, p.36).
In summary, a greater capacity for self-regulation enables students to solve mathematical problems effectively, thus providing them with tools for an improved understanding of problems they have, for the selection and use of appropriate strategies, and for the choice of high-quality objectives, the appropriate management of time and of the eventual imponderables that may occur during the task. Adequate self-regulation contributes to increased emotional control during the process of solving mathematical problems (Zimmerman, 2002; Zimmerman and Kitsantas, 2014).
In view of the points discussed so far, it is essential to have tools that can ascertain and, in particular, measure the level of student self-regulation in mathematical problem-solving contexts. Taking this need as a starting point and referencing the instrument constructed by Fernández-Gago and Marbán (2022) (aimed at secondary school students), this study aims to adapt and validate this instrument for university students.
The paradigm of this research is postpositivist, and the type of research conducted is descriptive. In this phase, the study aims to describe the educational situation of interest in this work as it presents itself in its natural context, without experimental manipulation, maintaining an objective and systematic approach in the collection and analysis of the data, but recognizing that a complete and definitive understanding of reality cannot be achieved. Thus, the approach of the present study, which is quantitative in nature, involves the application of an instrument, in the form of a Likert-type scale, which makes it possible to determine, in terms of different variables, the level of self-regulation of primary education teachers in initial training.
For the selection of the sample, non-probabilistic convenience or incidental sampling was used since the students who participated in the study were selected for their accessibility and suitability for the study.
A total of 269 preservice teachers from the three campuses of the University of the Basque Country (UPV/EHU) enrolled in the first year of the Degree in Primary Education in the 2020–2021 academic year participated in the validation process of the adapted scale. The characteristics of the selected sample are detailed in Table 1.
Table 1
Sample Data From the 2020–2021 Academic Year
|
Academic year |
||
|
2020/21 |
||
|
Variables |
n = 269 |
% |
|
Gender Identity |
||
|
Women |
200 |
74% |
|
Men |
63 |
23% |
|
Non-binary |
4 |
1% |
|
DK/NO (don´t know/no opinion) |
2 |
1% |
|
High School Modality |
||
|
Social Sciences |
138 |
51% |
|
Science and Technology |
122 |
45% |
|
Arts |
4 |
1% |
|
Others |
5 |
2% |
Note: derived from research.
According to data provided by the Educabase for the 2020–2021 period, 68% of enrollments in teacher education programs, such as the Bachelor’s Degree in Elementary Education (GEP), correspond to women. As shown in Table 1, the disproportion in the gender identity variable reflects this common trend in education-related programs in which the presence of women is greater than that of men.
In relation to previous studies (see Table 1), the trend of a greater number of students coming from social sciences modality than from the science and technology modality has been maintained over time (Asensio et al., 2022).
Each student voluntarily answered the online questionnaire. To this end, a letter of agreement was given to the students to inform them about the objective and procedure of the study, as well as to guarantee the privacy and confidentiality of the participants’ data. The questionnaire took approximately 15 minutes to complete.
Finally, this present project has been authorized by the Ethics Committee for research involving human subjects, their samples, and data (CEISH-UPV/EHU) with code M10_2021_087.
The instrument used in this study is based on the scale relating to self-regulation of learning in mathematical problem-solving contexts constructed by Marbán and Fernández-Gago (2022). The original questionnaire consists of 45 items that are answered on a 5-point Likert scale, each depending on the degree of agreement. The original validation process was carried out with high school students. However, it is important to note that the current scale has been adapted specifically for university students.
To ensure the relevance and validity of the scale adapted to the university setting, it is important to consider the particularities and characteristics specific to this context. University students face more complex academic challenges and cognitive demands than high school students do. In particular, in the process of solving mathematical problems, they are expected to employ more sophisticated self-regulation strategies than high school students do, to have a greater ability to set goals, to plan their studies more autonomously, to have better control of time management, and to self-reflect on their own learning. This requires carrying out an additional validation process with samples of university students, making adjustments in the classification of items, examining the internal structure, evaluating internal consistency, and carrying out content and face validity analyses.
The stages followed in the process of adaptation and validation of the scale are listed below: (1) content validation, (2) translation validation, (3) face validity, (4) internal reliability, and (5) analysis of the factor structure of the scale (exploratory factor analysis).
First, on the basis of the initial scale constructed by Marbán and Fernández-Gago (2022), which was subjected to expert judgment, the classification of the items by these two authors is evaluated not only in terms of the three components of Zimmerman’s model (dimension, phases and levels) but also in terms of Polya’s phases. In addition, in the original validation process, the questionnaire was studied in the context of secondary school students, whereas the current scale is aimed at university students; it is clear that this difference should be taken into account.
From this perspective, the content validity by experts who know the characteristics of this study sample and its sociocultural context implies the modification of some items. In some cases, this is due to its semantic complexity, of which an example is Item 28, “I am not able to play devil’s advocate to see if each step I take is correct,” which was replaced by “I am capable of being critical of myself, questioning the steps of my solution.” In other cases, it is due to their ambiguity, of which an example is Item 29, “I am able to write the solution with the corrected steps,” which was replaced by “I am able to sequence, describe, and correct the steps performed to reach the solution.” It should be noted that this item, for secondary school students, is broken down into two items: “I am able to order the steps that lead me to the solution of a problem and describe them” and “I am able to see how each step of my solution builds on the previous step”. For this reason, the questionnaire for university students consists of one fewer item than the one for secondary school students. At the end of this process of evaluation and item modification, the questionnaire adapted to university students consisted of 44 items.
In this study and in relation to the sample, i.e., students of the primary education undergraduate degree at the University of the Basque Country (UPV/EHU), it is important to consider their sociocultural context: this is a bilingual population, with Basque being the main language of instruction in their educational environment. Consequently, the validation process for the translation of the adapted scale into Basque has been carried out. The process of validating the translation of the questionnaire into Basque is essential to ensure that students understand the items correctly and can respond appropriately, which contributes to obtaining valid and reliable data in the specific context of the study.
To guarantee the quality of the translation and language equivalence, two stages were followed: (1) Forward or direct translation: in this phase, the items of the original scale in Spanish were translated into the new language (Basque) by an expert in mathematics education, and this translation was triangulated by a group of bilingual experts in the area, who evaluated the equivalence and comprehension of the items in Basque and suggested the necessary modifications in order to adapt them appropriately. (2) Reverse translation: in this second stage, the questionnaire translated into Basque was sent to another translation group composed of people who are fluent in Basque and Spanish and whose mother language is Basque. This group performed reverse translation, that is, they translated the questionnaire from Basque into Spanish, generating a new version in the original language. This new version in Spanish was compared with the original version of the questionnaire to evaluate equivalence and detect possible differences or discrepancies.
These two phases ensured that the items of the questionnaire translated into Basque maintained their equivalence with the original version in Spanish, and that they were understandable for the students who would answer the questionnaire in Basque.
Finally, face validity was checked to refine the wording and comprehension of the items. For this purpose, the adapted and translated questionnaire was piloted with a sample of 52 students (48 women, 4 men) in the third year of the degree in early childhood education at the University of the Basque Country. This sample had characteristics similar to those of the target population, i.e., students of the Faculty of Education of Bilbao whose knowledge of problem-solving was at the preuniversity level. The students’ regarding potentially problematic items were collected, and modifications were made to gradually outline the final questionnaire. For example, Item 40, “I don’t feel bad if I don’t solve the problem”—which generated certain comprehension problems—was replaced by “When I do not manage to solve a problem, I feel bad,” thus avoiding a double negative. In relation to this question, it was considered important to maintain negative items to detect and avoid acquiescence, among other things.
Finally, the self-regulation questionnaire (translated and adapted) consisted of 44 items (see Annex 1), organized in a Likert scale format of 7 response levels where 1 = never or almost never; 2 = approximately one in ten times; 3 = approximately one in three or four times; 4 = approximately 50% of the time; 5 = approximately two in three times; 6 = between eight and nine times in ten and 7 = always or almost always. The 7-point Likert scale is an update of the 5-point scale used by Marbán and Fernández-Gago (2022). The inclusion of two additional items in the 7-point Likert scale provided students with a greater range to express subtleties in their responses, avoiding the tendency to choose intermediate or neutral answers. With broader options, more precise and differentiated levels of agreement or disagreement could be captured, providing greater richness in the information collected (Formplus, 2021).
The data analysis was conducted with the statistical program SPSS, version 28.0 for Windows. With respect to the reliability of the instrument, in terms of internal consistency, a value of 0.778 was obtained for the Cronbach’s alpha coefficient of the total scale, a value commonly considered good by the scientific community in similar contexts. On the other hand, to analyze the factorial structure of the scale, an exploratory factor analysis (EFA) was performed This analysis is supported by a KMO index of 0.836 > 0.7 and a p-value of 0.000<0.05 in the Bartlett sphericity test, which is statistically significant (Landa, Berciano and Marbán, 2021).
As shown in Table 2, 3 items presented values lower than 0.1 in the corrected discrimination index, i.e., they were items that do not contribute significantly to the mediation of the construct of interest. These items were therefore progressively eliminated to improve the quality and accuracy of the questionnaire.
Table 2
Total Element Statistics
|
Total Item-total correlation |
Cronbach’s alpha if Item removed |
|
|
Item1 |
.275 |
.869 |
|
Item2 |
.393 |
.868 |
|
Item3 |
.009 |
.876 |
|
Item4 |
.468 |
.866 |
|
Item5 |
.637 |
.863 |
|
Item6 |
.273 |
.869 |
|
Item7 |
.068 |
.873 |
|
Item8 |
.414 |
.867 |
|
Item9 |
.508 |
.865 |
|
Item10 |
.355 |
.868 |
|
Item11 |
.370 |
.868 |
|
Item12 |
.392 |
.867 |
|
Item13 |
.341 |
.868 |
|
Item14 |
.543 |
.865 |
|
Item15 |
.203 |
.870 |
|
Item16 |
.174 |
.871 |
|
Item17 |
.530 |
.865 |
|
Item18 |
.182 |
.871 |
|
Item19 |
.486 |
.866 |
|
Item20 |
.430 |
.867 |
|
Item21 |
.349 |
.868 |
|
Item22 |
.571 |
.864 |
|
Item23 |
.601 |
.864 |
|
Item24 |
.335 |
.868 |
|
Item25 |
.542 |
.865 |
|
Item26 |
.336 |
.868 |
|
Item27 |
.267 |
.870 |
|
Item28 |
.304 |
.869 |
|
Item29 |
.440 |
.867 |
|
Item30 |
.619 |
.864 |
|
Item31 |
.358 |
.868 |
|
Item32 |
.605 |
.864 |
|
Item33 |
.446 |
.866 |
|
Item34 |
.162 |
.872 |
|
Item35 |
.483 |
.866 |
|
Item36 |
.197 |
.870 |
|
Item37 |
.115 |
.873 |
|
Item38 |
.108 |
.872 |
|
Item39 |
.237 |
.871 |
|
Item40 |
- .021 |
.876 |
|
Item41 |
.460 |
.866 |
|
Item42 |
.394 |
.867 |
|
Item43 |
.502 |
.865 |
|
Item44 |
.234 |
.870 |
Note: derived from research.
Item deletion is a common practice in scale validation, but it must be performed with great care and take other aspects into account, such as internal consistency and representativeness of the construct being measured. The process consists of deleting one item at a time and recalculating for each deletion the corrected discrimination value for the remaining items.
One of the criteria for considering the elimination of these items to be appropriate is that, after the process (see Annex 2), several of the remaining items either improve their correlation values, including those formulated negatively, or maintain values within the established criteria, which are all greater than 0.1. Another condition is that, although 4 items still do not meet the corrected item-total correlation criterion (<0.2), all 4 show improvement after the elimination process. In addition, the reliability results are consistent, with a Cronbach’s alpha value (α = 0.884) that hardly varies with the elimination of one item or another, thus suggesting keeping them as they are. The last piece of evidence is that they also improve the Cronbach’s α = 0.884, previously α = 0.778 and the Kaiser-Meyer-Olkin (KMO) value from 0.836 to 0.846. For all these reasons, the elimination of items (3, 7, 40) is justified and the total number of items of the adapted questionnaire stands at 41.
To assess construct validity, an exploratory factor analysis (EFA) was performed on the initial sample of 269 students using the 41 final items of the scale. The analysis employed the principal axis factor extraction method and subsequent varimax rotation.
A preliminary analysis revealed a resulting dimensional structure composed of twelve factors (see Annex 3) that together explained 61.76% of the variance. Among these factors, five were unidimensional, that is, they consisted of a single item each. Analysis of these items showed that they had loadings on other factors. Consequently, and in accordance with the six factors of the original questionnaire, the number of factors was reduced to seven (see Table 3). A seventh factor, composed of items formulated in the negative, was not present in the secondary school questionnaire.
Table 3
Factor Weights for the Exploratory Factor Analysis With Varimax Rotation of the Self-Regulation Scale in Mathematical Problem-Solving Contexts With 7 Factors
|
Scale |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
|---|---|---|---|---|---|---|---|
|
Factor 1 |
|||||||
|
Item30 |
.631 |
||||||
|
Item31 |
.573 |
||||||
|
Item33 |
.567 |
||||||
|
Item22 |
.491 |
||||||
|
Item32 |
.468 |
||||||
|
Item26 |
.459 |
||||||
|
Item23 |
.432 |
||||||
|
Factor 2 |
|||||||
|
Item2 |
.683 |
||||||
|
Item4 |
.573 |
||||||
|
Item5 |
.432 |
||||||
|
Item14 |
.402 |
||||||
|
Item1 |
.315 |
||||||
|
Item24 |
.285 |
||||||
|
Factor 3 |
|||||||
|
Item41 |
.589 |
||||||
|
Item42 |
.566 |
||||||
|
Item43 |
.483 |
||||||
|
Item39 |
.471 |
||||||
|
Item35 |
.259 |
||||||
|
Factor 4 |
|||||||
|
Item13 |
.619 |
||||||
|
Item10 |
.567 |
||||||
|
Item11 |
.552 |
||||||
|
Item12 |
.482 |
||||||
|
Item8 |
.286 |
||||||
|
Item17 |
.261 |
||||||
|
Item9 |
.259 |
||||||
|
Item6 |
.211 |
||||||
|
Factor 5 |
|||||||
|
Item18 |
.533 |
||||||
|
Item44 |
.528 |
||||||
|
Item27 |
.484 |
||||||
|
Item34 |
.459 |
||||||
|
Item38 |
.396 |
||||||
|
Item16 |
.375 |
||||||
|
Item37 |
.274 |
||||||
|
Factor 6 |
|||||||
|
Item21 |
.588 |
||||||
|
Item20 |
.551 |
||||||
|
Item19 |
.513 |
||||||
|
Item29 |
.299 |
||||||
|
Item25 |
.309 |
||||||
|
Factor 7 |
|||||||
|
Item28 |
.697 |
||||||
|
Item15 |
.584 |
||||||
|
Item36 |
.422 |
Note: derived from research.
The factors were then interpreted and described in terms of factor loadings, explained variances, and the content of the items included in each factor.
Factor 1: Students’ Perceptions of Their Ability and How This Influences Self-Regulation of the Resolution Process. The 7 items comprising this factor were located in the phases of problem-solving: carry out the plan and review the process. Most of them had to do with the behavioral dimension, although the motive dimension also played a role. In relation to the phases, both the during and the after phases predominated, while the level tended to be self-control or self-regulation.
The presence of the expression “I am able to” in several items indicates that self-efficacy is being assessed, that is, the students’ belief in their ability to successfully carry out the problem-solving process.
On the other hand, items related to the behavioral dimension, such as Item 22, “At all times I know what I am doing in a problem, what I am doing it for, and how what I am doing serves me in the solution,” focused on self-judgment, which is one of the key processes of Zimmerman’s (2002) self-reflection phase. These items explore how students perceive themselves during the problem-solving process, how they engage in challenges, and how they evaluate their own performance and progress.
For all of the above, a characterization of this factor can be the students’ perception of their ability and how this influences the self-regulation of the mathematical problem-solving process. This factor explains 22% of the variance, i.e., it has a notable influence on the self-regulation of the participants’ learning.
Factor 2: Ethics. This factor was composed of 6 items, 4 of which belonged to the comprehension problem-solving phase and 2 to carry out the plan. Regarding the dimensions, most of the items corresponded not only to behavior, but also to time. The phases were before and during. The levels were emulation or self-control.
Analyzing this factor, a common expression in Items 2, 4 and 5 was found: “Try … although” (I try to do something, even if it is difficult to understand; I try to solve, even if it causes me insecurity; I try to understand, even if I have doubts...); this refers to the personal quest to overcome difficulties.
The items corresponding to the time dimension refer to the idea of perseverance and patience. Item 14 states, “I dedicate time,” while Item 24 says, “I persist in carrying out my plan or idea, even if I am not sure if it is right,” both explicitly refer to the concept of persistence. In the same way, although in the opposite direction, Item 1 was also found in this factor: “I give up reading a problem as soon as its statement is longer than 5 lines”.
Therefore, this factor can be associated with ethics, understood as the responsibility with which each student consciously and fully accepts the task of solving the problem, pursuing objectives with perseverance, patience, and using their own resources (Marbán and Fernández-Gago, 2022).
Factor 3: Problem-Solving and Personal Growth. The 5 items comprising this factor did not belong to any problem-solving phase, i.e., their content was not directly related to specific stages of problem-solving. This finding suggests that this factor might be more associated with broader dimensions or aspects of self-regulated learning, such as motivation, perseverance, positive attitudes toward challenges, and commitment to personal growth. All the items belonged to the motives dimension. The phases were before and during. The level, in turn, was self-control or self-regulation.
A clear example of this factor is Item 43, “I think it is important that a problem is difficult to improve my training and to grow as a person”, which relates to the dimension of motivation and the perception of challenge. The item indicates that students value difficult problems as opportunities for learning and personal growth, showing a positive attitude toward challenges. Therefore, this factor can be characterized as problem-solving and personal growth.
Factor 4: Attitude Toward the Statement. Factor 4 comprised 8 items, of which 7 belonged to the problem-solving phase of comprehension. Regarding the dimension, most of them pertained to behavior, although some were classified under method or motive. The predominant phase was during, but also after, and one item was even classified under the before phase. The most repeated level was self-regulation, although self-control was also very present.
This factor can be characterized or labeled as attitude toward the statement. This characterization is exemplified by the fact that the term “statement” was common in all the items. Thus, Item 11, “If I have not managed to understand a statement, I try to look for the causes so that the same thing does not happen to me the next time,” deals with the students’ management of their own behavior, derived from their attitude toward the statement: a positive attitude toward the statement entails proactive behavior in the problem-solving process.
Factor 5: Negative Self-Efficacy Beliefs and External Causal Attribution. Self-Efficacy Beliefs and Negative Self-Judgment. This factor was composed of 7 negatively formulated items. The most repeated problem-solving phase was make a plan, while it should be noted that 4 items did not belong to any problem-solving. In relation to the dimensions, items within the problem-solving phases related to behavior, while those outside the problem-solving phases were associated with ethics. The most repeated phases were before and during. In reference to the level, most of them belonged to observation, the lowest level of self-regulation.
On the one hand, some items were characterized by the common expression “I am not capable”. An example of this is Item 16: “If I have a fixed idea of how to solve the problem I am not capable of changing it.”; Believing oneself incapable of changing ideas or approaching challenges in a flexible way may lead to a lack of confidence and avoidance of seeking new strategies or approaches.
On the other hand, there were items referring to the non-assumption of responsibility in the problem-solving task, attributing the cause of success or failure to external agents, which is evident in Item 38: “The main person responsible for the success of the problem is the teacher.” In this statement, success or failure in problem-solving is attributed to factors such as luck or the teacher’s help, which may diminish the feeling of control over learning and decrease intrinsic motivation.
Factor 6: Problem-Solving Method. This was composed of 5 items, most of which belonged to the problem-solving phase of make a plan, although one item was placed in carry out the plan and another in review the process. The predominant dimension was method. All items belonged to the during phase and the predominant level was emulation or self-control.
Analyzing the classification of the items, this factor alludes to the method used by the student to solve the problem, i.e., it refers to how the student acts and what type of strategies and processes they use to carry out the task. From this perspective, this factor includes Item 25, “I check my provisional conclusions (conjectures) or results to see if they are coherent or if the conditions of the statement are met.” This factor is therefore characterized as Problem-solving method.
Factor 7: Social Environment. This factor was composed of 3 items. One item belongs to the problem-solving phase of understanding, another to carry out the plan and the third did not belong to any problem-solving phase. The dimension was the social environment, the predominant phase was after, and the level of all the items ws self-regulation.
An example of this is Item 15 “If I do not understand a statement, I am able to ask for help to understand it”, in which it is observed how students ask for help to avoid blockages or overcome difficulties during the activity.
Seeking or asking for help is an excellent indicator of self-regulation; precisely, underachieving students are reluctant to ask for help because they do not know what, when, and how to ask, or whom to ask, and they are afraid of appearing incompetent.
In summary, these factors point to fundamental aspects of self-regulation and the problem-solving process, such as beliefs and attitudes, methods used, and the social environment.
Self-regulation levels. In relation to the levels of Zimmerman’s model, factor analysis also facilitated a comparison with certain aspects of the problem-solving phases. Thus, the items defined at the highest level of self-regulation were grouped into factors 1, 3, 4 and 7, i.e., students who reached this level were characterized by a positive attitude toward the statement, personal growth, positive self-judgment and the ability to ask for help from the environment. At the next level of self-regulation, self-control, students began to have some control over their own learning process, acquiring skills for evaluating their progress and detecting errors, among others. These aspects were reflected in factors 1, 2 and 4, although less predominantly. Factor 2, ethics, showed the highest concentration of items related to the self-regulation level. In this factor, the students assumed responsibility for the task consciously and fully. The level of emulation related mainly to factor 6, method, which refers to the strategies that students use in problem-solving, such as looking for examples or previous models that can serve as a reference to solve a problem. At the emulation level, students sought to imitate previous successful approaches to problem-solving. From this perspective, the emulation level is part of this factor 6. Finally, the lowest level of self-regulation, observation, related to factor 5, since all the items defined at this level fell into this factor, which refers to negative self-efficacy beliefs and external causal attribution, i.e., students at this level are characterized by a lack of responsibility and self-regulation skills to solve problems (see Annex 4).
The results obtained in the validation process of the adapted instrument show that it meets the established criteria in terms of internal consistency and factorial structure. In fact, the existence of the factors, which are theorized and constructed from the literature, is supported by exploratory factor analysis.
Thus, in factor 1, self-efficacy and self-judgment appear together, two core aspects of self-regulation of learning (Zimmerman, 2002). Both constructs influence how students face mathematical problems, how they become involved in solving them and how they evaluate their own performance (Usher and Pajares, 2008). This factor shows that the two constructs, self-efficacy, and self-judgment, are closely related and complement each other in the process of solving mathematical problems. Factor 2, characterized as ethics, is a new dimension of self-regulation of learning in problem-solving contexts defined by Marbán and Fernandez-Gago (2022). The inclusion of this dimension, described and justified in the theoretical framework, seems to be relevant, as it provides a new perspective on student responsibility and engagement in mathematical problem-solving. Factor 3, personal growth, is related to the motive dimension, in relation to goal orientation, a dimension that appears in Zimermman’s (2002) model. Factor 4, attitude toward the statement, relates to behavior, a characteristic dimension of self-regulated learning. The theoretical framework already points to attitude as a factor influencing mathematics performance (Luttenberger, Wimmer and Paechter, 2018). It should be noted that factor 5, self-efficacy beliefs and negative self-judgment, is related to factor 1 in terms of self-efficacy and self-judgment but differs in the negative formulation of the items. Both factors 6 and 7, characterized as method and social environment, respectively, are dimensions of self-regulation in Zimmerman’s (2002) model (see Annex 5).
In short, the latent structure identified by the EFA accords with the item classification established from the theoretical framework used. Each identified factor has a clear relationship with key aspects of self-regulated learning, such as attitudes toward statements, self-efficacy beliefs, methods used and the social environment. These factors provide valuable information on how students self-regulate in mathematical problem-solving and can help to understand better the processes involved in this task.
However, the items also classified by phases (before, during and after) are not always grouped explicitly in the scale. This may be because students, when answering the questionnaire, do not clearly distinguish between the different phases or moments in the problem-solving process according to Polya’s approach. Pintrich (2004) and other studies, such as those by Núñez, Amieiro, Álvarez, García, and Dobarro (2015), have highlighted the difficulty of separating some of the phases and the lack of hierarchy or linearity in their structure.
In this context, it is worthwhile to stop and examine, even in a cursory manner, how the phases of the classical models of mathematical problem-solving intertwine with the processes of self-regulation. These phases of problem-solving according to Polya overlap with the phases of Zimmerman’s model, which include the self-reflection phase (understanding the task and evaluating beliefs and motivation), the planning phase (setting goals and strategies), the execution phase (implementing strategies) and the subsequent self-reflection phase (evaluating performance and making adjustments) (see Annex 6).
Originally, the instrument by Marbán and Fernández-Gago was aimed at secondary school students; the adaptation described in this article was aimed at university students. Some factors in the two versions of the instrument are very similar. In terms of differences, the most noteworthy one is that Marbán and Fernández-Gago’s instrument required the elimination of negatively worded items. One explanation given by these authors in this respect involves the possibility that these items may provoke a defensive attitude in adolescent students, i.e., that they may feel judged and avoid becoming too involved in their responses. However, this elimination of items was not necessary for university students, as these items constituted factor 5: negative self-efficacy beliefs and external causal attribution. Hypothesizing that the reason for this difference between the target populations could have to do with a higher level of self-regulation of university students with respect to high school students would contradict some of the evidence collected, such as the findings of the study by Cleary and Chen (2009), which point in the opposite direction.
In summary, and as noted in the theoretical framework, the construct of self-regulation of learning is complex and multidimensional (Zimmerman and Kitsantas, 2014). In the instrument adapted and validated for university students in mathematical problem-solving contexts, 7 dimensions have been identified and characterized. These dimensions are intertwined and interrelated, with the boundaries between them sometimes being quite blurred. Thus, a negative self-efficacy belief can influence the attitude toward the statement (Araya and Moreira-Mora, 2016) and, in turn, affect the way in which the action plan is proposed, and the resolution is carried out.
The results of the exploratory factor analysis address the gap detected in the theoretical framework, especially in its more operational version, and suggest that the adapted and validated scale is a useful tool for measuring the level of self-regulation among university students in problem-solving contexts. This will enable more precise and relevant information on the self-regulation skills and strategies of students at this educational level. Likewise, the results provide guidance for the confirmatory factor analysis (CFA) that allow for the continuation of the research.
Although this scale has satisfactory psychometric properties, it should be noted that, in its current state, it is not without limitations. Thus, considering the relative novelty of the instrument and the fact that self-regulation is a complex and multidimensional construct, there may be limitations related to conceptual issues concerning the validity of the item bank and its initial selection. On the other hand, the variables in this study should not be considered the only conceivable possibilities; new variables can be contemplated and taken into consideration, without detriment to the validity of the present study, which contributes to broadening the perspectives for explaining the complex world of self-regulation in future mathematics teachers.
This study indicates that self-regulation is a construct that differentiates students, i.e., it suggests the existence of different self-regulation profiles in relation to the resolution of mathematical problems that characterize students at the primary education undergraduate degree. Therefore, for future research, identifying these profiles and designing specific interventions aimed at improving them would be interesting.
In short, this research opens new opportunities for understanding and promoting self-regulation in mathematical learning and, in particular, in mathematical problem-solving contexts. This is fundamental for the achievement of sustainable development goals and the promotion of quality education.
Work partially supported by Research Group GIU21/031 of the University of the Basque Country (UPV/EHU), Spain.
Each student voluntarily answered the online questionnaire. To this end, a consent letter was given to the students to inform them about the objective and procedure of the study, as well as to guarantee the privacy and confidentiality of the participants’ data.
This present project has been authorized by the Ethics Committee for research involving human subjects, their samples and data (CEISH-UPV/EHU) with code M10_2021_087.
-The authors declare no conflict of interests.
All the authors declare that the final version of this paper was read and approved.
Authors and CRediT Roles: J.L.: Conceptualization, Formal Analysis, Writing - Review & Editing. A.B.: Conceptualization, Formal Analysis, Writing - Review & Editing, Supervision. J.M.M.: Conceptualization, Formal Analysis, Writing - Review & Editing, Supervision.
The total contribution percentage for this paper was as follows: J.L. 33,3%, A.B. 33,3% y J.M.M. 33,3%.
The data supporting the results of this study will be made available by the corresponding author, J.L., upon reasonable request.
A Preprint version of this paper was deposited in: https://doi.org/10.5281/zenodo.8337461
Alguacil, M., Boqué, M., & Pañellas, M. (2016). Dificultades en conceptos matemáticos básicos de los estudiantes para maestro. International Journal of Developmental and Educational Psychology. Revista INFAD de Psicología, 1(1), 419-430. https://doi.org/10.17060/ijodaep.2016.n1.v1.162
Araya, R. G., & Moreira-Mora, T. E. (2016). Un modelo explicativo de las creencias y actitudes hacia las matemáticas: Un análisis basado en modelos de ecuaciones estructurales. Avances de Investigación en Educación Matemática, 10, 27-51. https://doi.org/10.35763/aiem.v0i10.155
Asensio Muñoz, I., Arroyo Resino, D., Ruiz-Lázaro, J., Sánchez-Munilla, M., Ruiz de Miguel, C., Constante-Amores, A., & Navarro-Asencio, E. (2022). Perfil de acceso a la universidad de los maestros en España [University access profile of teachers in Spain]. Educación XXI, 25(2), 39-63. https://doi.org/10.5944/educxx1.31924
Bembenutty, H., White, M. C., & Vélez, M. R. (2015). Developing Self-regulation of Learning and Teaching Skills among Teacher Candidates. New York, NY: Springer. https://doi.org/10.1007/978-94-017-9950-8
Boekaerts, M. (1997). Self-regulated learning: A new concept embraced by researchers, policy makers, educators, teachers, and students. Learning and instruction, 7(2), 161-186. https://doi.org/10.1016/S0959-4752(96)00015-1
Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. John Wiley & Sons.
Caballero, A., Cárdenas, J., & Gordillo, F. (2016). La intervención en variables afectivas hacia las matemáticas y la resolución de problemas matemáticos. El MIRPM. In J. A. Macías, A. Jiménez, J. L. González, M. T. Sánchez, P. Hernández, C. Fernández, F. J. Ruiz, T. Fernández y A. Berciano (Eds.), Investigación en Educación Matemática XX (pp.75-91). Málaga: SEIEM.
Callan, G.L. (2014). Self-regulated Learning (SRL) Microanalysis for Mathematical Problem Solving: A Comparison of a SRL Event Measure, Questionnaires, and a Teacher Rating Scale. Theses and Dissertations. 557. https://dc.uwm.edu/etd/557
Chen, Q., & Lo, J. (2019). Preservice Teachers’ Mathematics Anxiety and Mathematics Teacher Efficacy: The Roles of Anticipatory Emotions and Regulatory Strategies. Journal of Teacher Education, 70(3), 267-283.
Cleary, T. J., & Chen, P. P. (2009). Self-regulation, motivation, and math achievement in middle school: Variations across grade level and math context. Journal of School Psychology, 47(5), 291-314. https://doi.org/10.1016/j.jsp.2017.04.004
Cleary, T. J., Velardi, B., & Schnaidman, B. (2017). Effects of the Self-Regulation Empowerment Program (SREP) on middle school students’ strategic skills, self-efficacy, and mathematics achievement. Journal of School Psychology, 64, 28-42. https://doi.org/10.1016/j.jsp.2017.04.004
Dignath, C., & Büttner, G. (2018). Components of fostering self-regulated learning among students. A meta-analysis on intervention studies at primary and secondary school level. Metacognition and Learning, 13(2), 169-195.
Döhrmann, M., Kaiser, G., & Blömeke, S. (2014). The conceptualisation of mathematics competencies in the international teacher education study TEDS-M. In S. Blömeke, F. J. Hsieh, G. Kaiser and W. H. Schmidt (Eds.), International Perspectives on Teacher Knowledge, Beliefs and Opportunities to Learn (pp. 431- 456). Drodrecht, Países Bajos: Springer. https://doi.org/10.1007/978-94-007-6437-8_20
Efklides, A. (2011). Interactions of metacognition with motivation and affect in self-regulated learning: The MASRL model. Educational Psychologist, 46(1), 6-25. https://doi.org/10.1080/00461520.2011.538645
Fernández-Gago, J., & Marbán, J. M. (2022). Diseño y validación de un instrumento para medir autorregulación en el alumnado de secundaria en contextos de resolución de problemas. Manuscrito en preparación.
Formplus. (2021). La escala Likert de 4, 5 y 7 puntos + [Ejemplos de cuestionarios]. Retrieved May 3, 2021, from https://www.formpl.us/blog/point-likert-scale
García, J. E. (2019). La formación permanente del profesorado de matemáticas en primaria: una necesidad ignorada. Uno: revista de didáctica de las matemáticas. 83, 42-46
Gutiérrez-Gutiérrez, A., Gómez, P., & Rico, L. (2016). Conocimiento matemático sobre números y operaciones de los estudiantes de Magisterio [Mathematical knowledge of numbers and operations in spanish future primary teachers]. Educación XXI, 19(1), 135-158. https://doi.org/10.5944/educXX1.15581
Hadwin, A., Järvelä, S., & Miller, M. (2018). Self-regulation, co-regulation, and shared regulation in collaborative learning environments. In D. H. Schunk and J. A. Greene (Eds.), Handbook of self-regulation of learning and performance (pp. 83-106). Routledge/Taylor and Francis Group. https://doi.org/10.4324/9781315697048-6
Harding, S.-M., English, N., Nibali, N., Griffin, P., Graham, L., Alom, B., & Zhang, Z. (2019). Self-regulated learning as a predictor of mathematics and reading performance: A picture of students in grades 5 to 8. Australian Journal of Education, 63(1), 74-97. https://doi.org/10.1177/0004944119830153
INEE (2013). TEDS-M, Estudio Internacional sobre la formación inicial en matemáticas de los maestros. Informe Español. Volumen II. Análisis secundario. Madrid, MECD.
Karunakaran, M.S. (2020). Opportunities to decrease elementary prospective teachers’ mathematics anxiety. The Mathematics Enthusiast, 17(2-3), 469-492. https://doi.org/10.54870/1551-3440.1495
Lachapell, G. (2017). La formación didáctico matemática del docente de la República Dominicana. Transformación, 13(3), 327-337
Landa, J., Berciano, A., & Marbán, J. M. (2021). Autorregulación y resolución de problemas matemáticos en el alumnado del grado en Educación Primaria. In Diago, P. D., Yáñez D. F., González-Astudillo, M. T. y Carrillo, D. (Eds.), Investigación en Educación Matemática XXIV (p. 662). Valencia: SEIEM.
Luttenberger, S., Wimmer, S., & Paechter, M. (2018). Spotlight on math anxiety. Psychology Research and Behavior Management, 11, 311–322. https://doi.org/10.2147/prbm.s141421
Marbán, J.M., Palacios, A., & Maroto. (2021). A. Enjoyment of teaching mathematics among pre-service teachers. Mathematics Education Research Journal, 33(3), 613-629. https://doi.org/10.1007/s13394-020-00341-y
Marbán, J.M., & Fernández-Gago, J. (2022). Mathematical Problem Solving through the Lens of Ethics and Aristotelian Attitude: A Case Study. Mathematics 10, 2565. https://doi.org/10.3390/math10152565
Mizala, A., Martínez, S., & Martínez, F. (2015). Pre-service Elementary School Teachers’ Expectations about Student Performance: How their Beliefs are affected by their Mathematics Anxiety and Student’s Gender. Teaching and Teacher Education, 50, 70-78. https://doi.org/10.1016/j.tate.2015.04.006
Ministerio de Educación and Formación Profesional (2018). PISA 2018, Programa para la Evaluación Internacional de los Estudiantes. Informe español. Madrid. Recuperado de https://www.educacionyfp.gob.es/inee/evaluaciones-internacionales/pisa/pisa-2018.htm
Ministerio de Educación and Formación Profesional (2020). TIMSS 2019. Estudio internacional de tendencias en matemáticas y ciencias. Informe español. Ministerio de Educación y Formación Profesional.
Muñoz-Fernández, G.A., Rodríguez-Gutiérrez, P., & Luque-Vílchez, M. (2019). La formación inicial del profesorado de educación secundaria en españa: perfil y motivaciones del futuro docente. [Initial teacher training for secondary education in Spain: profile and motivations of the future teaching staff]. Educación XX1, 22(1), 71-92. https://doi.org/10.5944/educXX1.20007
Nájera Saucedo, J., Salazar Garza, M. L., Vacio Muro, M.A., & Morales Chiané, S. (2020). Evaluación de la autoeficacia, expectativas y metas académicas asociadas al rendimiento escolar. Revista de Investigación Educativa, 38(2), 435-452. http://dx.doi.org/10.6018/rie.350421
Nortes Martínez-Artero, R., & Nortes Checa, A. (2017). Competencia matemática, actitud y ansiedad hacia las Matemáticas en futuros maestros. Revista Electrónica Interuniversitaria de Formación del Profesorado, 20(3), 145‐160. http://dx.doi.org/10.6018/reifop.20.3.290841
Nortes, R., & Nortes, A. (2018). Conocimientos matemáticos de futuros maestros en resolución de problemas de 6º de primaria. Educatio Siglo XXI, 36(3), 201-230. https://doi.org/10.6018/j/349971
Núñez, J., Amieiro, N., Álvarez, D., García, T., & Dobarro, A. (2015). Escala de Evaluación de la Autorregulación del Aprendizaje a partir de Textos (ARATEXR). European Journal of Education and Psychology 8(1), 9-22. https://doi.org/10.1016/j.ejeps.2015.10.002
Panadero, E., & Alonso-Tapia, J. (2014). ¿Cómo autorregulan nuestros alumnos? Modelo de Zimmerman sobre estrategias de aprendizaje. Anales de Psicología / Annals of Psychology, 30(2), 450–462. https://doi.org/10.6018/analesps.30.2.167221
Pintrich, P.R. (2004). A conceptual framework for as sessing motivation and self-regulated learning in college students. Educational Psychology Review, 16(4), 385-407. https://doi.org/10.1007/s10648-004-0006-x
Polya, G. (1990). How To Solve It (2nd edition). Penguin, London.
Sakiz, G., Pape, S. J., & Hoy, A. W. (2012). Does perceived teacher affective support matter for middle school students in mathematics classrooms? Journal of School Psychology, 50(2), 235–255. https://doi.org/10.1016/j.jsp.2011.10.005
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. En D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334-370). MacMillan.
Schoenfeld, A. (2018). Video analyses for research and professional development: the teaching for robust understanding (TRU) framework. ZDM, 50, 491-506. https://doi.org/10.1007/s11858-017-0908-y
Segarra, J., Bueno, A., Barrazueta, J., & Juliá, C. (2021). Estudio de la autoeficacia de las enseñanzas de matemáticas de los estudiantes de cuarto año de la Universidad del Azuay y la Universitat Rovira i Virgili. PNA 16(1), 78-97. https://doi.org/10.30827/pna.v16i1.18519
Segarra, J., & Juliá, C. (2021). Mathematical knowledge of elementary education student teachers: variable analysis. (2021). Uniciencia, 35(1), 124-138. https://doi.org/10.15359/ru.35-1.8
Schunk, D. H., and Usher, E. L. (2018). Social cognitive theoretical perspective of self-regulation. En D. H. Schunk and J. A. Greene (Eds.), Handbook of self-regulation of learning and performance (pp. 19–35). Routledge/Taylor & Francis Group. https://doi.org/10.4324/9781315697048-2
Suárez, J. M., Fernández, A. P., & Zamora, Á. (2018). Academic Goals in Relation to Motivational Self - regulation Value Strategies, REDIE, 20(2), 15-24. https://doi.org/10.24320/redie.2018.20.2.1689
Throndsen, I. (2011). Self-regulated learning of basic arithmetic skills: A longitudinal study. British journal of educational psychology, 81(4), 558-578.
Tzohar-Rozen, M., & Kramarski, B. (2017). Metacognition and Meta-Affect in Young Students: Does It Make a Difference in Mathematical Problem Solving? Teachers College Record, 119(13), 1-26. https://doi.org/10.1177/016146811711901308
UNESCO [Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura] (2016). Educación 2030. Declaración y Marco de Acción de Incheon. Hacia una educación de calidad inclusiva y equitativa y un aprendizaje a lo largo de la vida para todos. París, UNESCO. http://www.uis.unesco.org/Education/Documents/incheon-frameworkfor-action-en.pdf
Usher, E. L., and Pajares, F. (2008). Self-efficacy for self-regulated learning: A validation study. Educational and Psychological Measurement, 68, 443-463. https://doi.org/10.1177/0013164407308475
White, M. C., and DiBenedetto, M. K. (2018). Self-regulation: An integral part of standards-based education. In D. H. Schunk y J. A. Greene (Eds.), Handbook of self-regulation of learning and performance (pp. 208–222). Routledge/Taylor y Francis Group. https://doi.org/10.4324/9781315697048-14
Zamora, J. (2020). Las actitudes hacia la matemática, el desarrollo social, el nivel educativo de la madre y la autoeficacia como factores asociados al rendimiento académico en matemática. Uniciencia, 34(1), 74–87. https://doi.org/10.15359/ru.34-1.5
Zimmerman, B. J. (2002). Becoming a self-regulated learner: An overview. Theory into practice, 41(2), 64-70. https://doi.org/10.1207/s15430421tip4102_2
Zimmerman, B. J. (2013). From cognitive modeling to self-regulation: A social cognitive career path. Educational Psychologist, 48(3), 135-147. https://doi.org/10.1080/00461520.2013.794676
Zimmerman, B. J., and Kitsantas, A. (2014). Comparing students’ self-discipline and self-regulation measures and their prediction of academic achievement. Contemporary Educational Psychology, 39(2), 145-155.
Zimmerman, B. J., and Moylan, A. R. (2009). Self-regulation: Where metacognition and motivation intersect. En D. J. Hacker, J. Dunlosky, y A. C. Graesser (Eds.), Handbook of metacognition in education (pp. 299-315). New York, NY, US: Routledge/Taylor y Francis Group.
Annex 1.
Questionnaire on Self-Regulation of Learning in Problem-Solving Contexts (English Version)
|
No. |
Statement |
|---|---|
|
1 |
I stop reading a problem as soon as the problem statement is more than 5 lines long. |
|
2 |
If the statement is difficult to understand, I read it several times and try to understand it. |
|
3 |
If the statement is long (more than 5 lines), I relate it to others I have made or seen before. |
|
4 |
Even if a problem statement makes me unsure, I try to solve the problem. |
|
5 |
When I try to understand a problem, even if I have doubts, I don’t give it up because I take responsibility for solving it. |
|
6 |
After reading a problem statement I highlight or represent the essential conditions or information of the problem. |
|
7 |
After reading about the problem, I’m going to do the first thing that comes to my mind |
|
8 |
If I don’t understand the statement I talk to myself to try to understand it. |
|
9 |
If I feel insecure when I read a statement, I have resources to feel more confident. |
|
10 |
As I’m reading, I encourage myself by reminding myself that understanding the statement depends on what I try and how I try. |
|
11 |
If I have failed to understand a statement, I try to look for the causes so that the same thing does not happen to me the next time. |
|
12 |
Even if a problem seems useless or uninteresting to me, before I start to solve it, I try to motivate myself by reminding myself how important it is to learn it in order to pass the exam and the subject, and thus finish the course, the degree,... |
|
13 |
If I have understood the statement of a problem, I look at what worked for me in order to repeat or improve it in the next problem. |
|
14 |
I tend to keep in the habit of taking time to understand the issues. |
|
15 |
If I don’t understand a statement I am able to ask for help to understand it. |
|
16 |
If I have a fixed idea of how to solve the problem I am not capable to change it. |
|
17 |
After understanding the statement I think of different strategies to deal with it (try examples, start with simpler cases, change the statement, look for similar problems, look for regularities, etc.). |
|
18 |
After a while of weighing up plans, I’m not usually clear about which one I’m going to choose. |
|
19 |
Before writing a tentative conclusion about the solution (conjecture) I think about whether it makes sense. |
|
20 |
I am able to express my tentative conclusions about the solution (guesses), even if I don’t know if they are right. |
|
21 |
I am able to express my tentative conclusions about the solution (conjectures) even though I am embarrassed to express them. |
|
22 |
At all times I know what I am doing on a problem, what I am doing it for and how what I am doing is useful for the solution. |
|
23 |
If, after overcoming a difficulty, another difficulty arises in the problem, I look for ways to overcome it myself. |
|
24 |
I persist in pursuing my plan or idea, even if I am not sure if it is right. |
|
25 |
I check my tentative conclusions (conjectures) or results to see if they are consistent or if the conditions of the statement are met. |
|
26 |
I am able to control my emotions while solving a problem. |
|
27 |
If, when I check a solution, I realise that it is wrong, I am not able to take advantage of what is right to look for another way. |
|
28 |
If, after thinking about the problem for a long time, I am not able to solve it, I am able to ask for help from one of my classmates, teachers or people close to me. |
|
29 |
I am able to be critical of myself, questioning the steps of my solution. |
|
30 |
I am able to sequence, describe and correct the steps taken to reach the solution. |
|
31 |
I am able to see the possibilities of my solution to extend it to other problems. |
|
32 |
I am able to take an interest in other solutions and see the advantages or disadvantages with my own solution. |
|
33 |
I prefer challenging tasks (therefore a bit more difficult and adventurous) to exercises where I know what I have to do. |
|
34 |
I don’t engage in challenges that cause me fear, or stress or frustration or any negative emotions. |
|
35 |
I find it important when solving problems to do it myself. |
|
36 |
If I don’t know how to do it myself, I find it important to learn from my peers. |
|
37 |
I am not primarily responsible for the resolution of the problem. |
|
38 |
The main person responsible for the problem is the teacher. |
|
39 |
I am capable of thinking, even for a week, about a problem that has not come up. |
|
40 |
When I can’t solve a problem, I feel bad. |
|
41 |
When I’m solving problems, I’m so focused that it’s as if time stands still. |
|
42 |
I believe that being responsible and putting all interest in solving problems is not only beneficial for me, but also for parents, teachers and classmates. |
|
43 |
I think it is important that a problem is difficult in order to improve my education and to grow as a person. |
|
44 |
If the problem is difficult, I am not able to generate positive emotions for its resolution. |
Total Element Statistics
|
Total Item-total correlation |
Cronbach’s alpha if Item removed |
Note: derived from research.
Annex 2
Total Element Statistics
|
Total Item-total correlation |
Cronbach’s alpha if Item removed |
|
|---|---|---|
|
Item1 |
,273 |
,883 |
|
Item2 |
,383 |
,881 |
|
Item4 |
,468 |
,880 |
|
Item5 |
,645 |
,877 |
|
Item6 |
,266 |
,883 |
|
Item8 |
,405 |
,880 |
|
Item9 |
,525 |
,878 |
|
Item10 |
,339 |
,882 |
|
Item11 |
,347 |
,882 |
|
Item12 |
,368 |
,881 |
|
Item13 |
,325 |
,882 |
|
Item14 |
,537 |
,879 |
|
Item15 |
,205 |
,883 |
|
Item16 |
,192 |
,884 |
|
Item17 |
,526 |
,879 |
|
Item18 |
,210 |
,884 |
|
Item19 |
,475 |
,880 |
|
Item20 |
,426 |
,880 |
|
Item21 |
,357 |
,881 |
|
Item22 |
,572 |
,877 |
|
Item23 |
,606 |
,878 |
|
Item24 |
,348 |
,882 |
|
Item25 |
,540 |
,879 |
|
Item26 |
,375 |
,881 |
|
Item27 |
,277 |
,883 |
|
Item28 |
,306 |
,882 |
|
Item29 |
,437 |
,880 |
|
Item30 |
,633 |
,878 |
|
Item31 |
,370 |
,881 |
|
Item32 |
,602 |
,877 |
|
Item33 |
,464 |
,879 |
|
Item34 |
,179 |
,885 |
|
Item35 |
,489 |
,879 |
|
Item36 |
,205 |
,883 |
|
Item37 |
,120 |
,886 |
|
Item38 |
,105 |
,885 |
|
Item39 |
,225 |
,885 |
|
Item41 |
,447 |
,880 |
|
Item42 |
,395 |
,881 |
|
Item43 |
,513 |
,879 |
|
Item44 |
,255 |
,883 |
Note: derived from research.
Annex 3
Factor Weights for Exploratory Factor Analysis with Varimax Rotation of the Self-Regulation Scale in Mathematical Problem-Solving Contexts
|
Nº |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Factor 1 |
||||||||||||
|
item30 |
.666 |
.243 |
.178 |
.117 |
.109 |
.155 |
-.108 |
|||||
|
item33 |
.600 |
-.105 |
.249 |
.192 |
-.190 |
-.114 |
.327 |
.184 |
||||
|
item31 |
.570 |
.167 |
||||||||||
|
item9 |
.548 |
.112 |
.240 |
.206 |
.120 |
|||||||
|
item22 |
.527 |
.186 |
.109 |
.177 |
.189 |
.116 |
-.101 |
.154 |
||||
|
item32 |
.496 |
.133 |
.127 |
.279 |
.310 |
.164 |
.151 |
|||||
|
item23 |
.470 |
.437 |
.133 |
.228 |
.145 |
|||||||
|
item26 |
.453 |
.209 |
.118 |
|||||||||
|
item17 |
.444 |
.228 |
.161 |
.232 |
.116 |
.218 |
-.161 |
|||||
|
item35 |
.397 |
.259 |
.218 |
.138 |
.304 |
.187 |
.111 |
|||||
|
item29 |
.287 |
.265 |
.154 |
.273 |
-.125 |
.142 |
.148 |
|||||
|
Factor 2 |
||||||||||||
|
item2 |
.659 |
.117 |
||||||||||
|
item4 |
.275 |
.569 |
.157 |
.257 |
||||||||
|
item25 |
.167 |
.504 |
.333 |
.145 |
.102 |
.111 |
.142 |
-.102 |
||||
|
item8 |
.164 |
.470 |
.143 |
.321 |
-.135 |
-.140 |
-.176 |
-.209 |
||||
|
item6 |
.454 |
.187 |
-.179 |
|||||||||
|
item14 |
.176 |
.440 |
.296 |
.272 |
.153 |
-.113 |
.143 |
.193 |
.150 |
|||
|
item5 |
.409 |
.435 |
.156 |
.178 |
.104 |
.150 |
.220 |
.232 |
||||
|
i1REC |
.325 |
.276 |
.156 |
.104 |
||||||||
|
Factor 3 |
||||||||||||
|
item13 |
.210 |
.600 |
.159 |
.141 |
-.147 |
|||||||
|
item11 |
.258 |
.589 |
.231 |
.122 |
-.146 |
|||||||
|
item12 |
.110 |
.120 |
.561 |
.173 |
.118 |
.159 |
||||||
|
item10 |
.264 |
.135 |
.517 |
.142 |
-.321 |
|||||||
|
Factor 4 |
||||||||||||
|
item41 |
.269 |
.203 |
.100 |
.608 |
||||||||
|
item42 |
.167 |
.191 |
.582 |
.152 |
.143 |
|||||||
|
item43 |
.389 |
.453 |
.164 |
.220 |
.109 |
.121 |
||||||
|
Factor 5 |
||||||||||||
|
item20 |
.190 |
.109 |
.148 |
.672 |
.102 |
-.108 |
||||||
|
item19 |
.313 |
.184 |
.551 |
.231 |
.140 |
|||||||
|
item21 |
.291 |
.503 |
.120 |
.101 |
-.104 |
.248 |
||||||
|
Factor 6 |
||||||||||||
|
item44 |
.173 |
.613 |
||||||||||
|
item34 |
.494 |
.112 |
-.118 |
|||||||||
|
item27 |
.173 |
.428 |
.111 |
-.363 |
||||||||
|
item16 |
.211 |
-.139 |
.390 |
.149 |
.115 |
|||||||
|
item38 |
-.103 |
.102 |
-.172 |
.172 |
.318 |
-.131 |
.157 |
.128 |
-.142 |
|||
|
Factor 7 |
||||||||||||
|
item15 |
.138 |
.758 |
||||||||||
|
item28 |
.223 |
.132 |
.177 |
.598 |
.210 |
|||||||
|
Factor 8 |
||||||||||||
|
item37 |
.104 |
.156 |
.596 |
|||||||||
|
Factor 9 |
||||||||||||
|
item36 |
.181 |
.129 |
.185 |
.624 |
-.152 |
|||||||
|
Factor 10 |
||||||||||||
|
item39 |
.113 |
.374 |
-.192 |
.494 |
||||||||
|
Factor 11 |
||||||||||||
|
item18 |
.231 |
-.224 |
.375 |
.215 |
-.145 |
.614 |
-.100 |
|||||
|
Factor 12 |
||||||||||||
|
item24 |
.225 |
.263 |
.274 |
-.110 |
.115 |
.456 |
Note: Factor weightings >10.
Note: derived from research.
Annex 4
Distribution of Items According to the Level of Self-Regulation
|
Level of self-regulation |
||||
|
Factors |
Observation |
Emulation |
Self-control |
Self-regulation |
|
Factor 1 |
23, 26, 30 |
22, 31, 32, 33 |
||
|
Factor 2 |
1, 24 |
2, 4, 5, 14, |
||
|
Factor 3 |
39, 41 |
35, 42, 43 |
||
|
Factor 4 |
6, 8, 17 |
9, 10, 11, 12, 13 |
||
|
Factor 5 |
16, 34, 37, 38 |
18, 44 |
27 |
|
|
Factor 6 |
19, 20, 25, 29 |
21 |
||
|
Factor 7 |
15, 28, 36 |
|||
Note: derived from research.
Annex 5
Distribution of Items According to Zimmerman’s Dimensions
|
Factors |
Zimermann |
Boekarts |
||||||
|
Method |
Motives |
Behavior |
Time |
Social environment |
Ethic |
|||
|
Factor 1 |
30, 32, 33 |
22, 23, 26, 31 |
||||||
|
Factor 2 |
2 |
4, 5, 24 |
1, 14 |
5 |
||||
|
Factor 3 |
35, 39, 41, 42, 43 |
|||||||
|
Factor 4 |
6, 8, 17 |
6, 12 |
9, 10, 11, 13 |
|||||
|
Factor 5 |
27, 34, 44 |
16, 27, 18 |
18 |
34, 37, 38, 44 |
||||
|
Factor 6 |
19, 20, 21, 29 |
25 |
||||||
|
Factor 7 |
15, 28, 36 |
|||||||
Note: derived from research.
Annex 6
Distribution of Items in Problem-Solving Phases
|
Mathematical problem solving phases |
Do not belong to any phase |
|||||
|
Factors |
Understand the problem |
Make a plan |
Execute the plan |
Look back and reflect |
||
|
Factor 1 |
22, 23, 26 |
30, 31, 32 |
33 |
|||
|
Factor 2 |
1, 2, 5, 14 |
4, 24 |
||||
|
Factor 3 |
35, 39, 41, 42, 43 |
|||||
|
Factor 4 |
6, 8, 9, 10, 11, 12, 13 |
17 |
||||
|
Factor 5 |
16, 18 |
27 |
34, 37, 38, 44 |
|||
|
Factor 6 |
19, 20, 21 |
25 |
29 |
|||
|
Factor 7 |
15 |
28 |
36 |
|||
Note: derived from research.
1* Corresponding author
Josune Landa, josune.landa@ehu.eus, https://orcid.org/0009-0009-9683-2023
Ainhoa Berciano, ainhoa.berciano@ehu.eus, https://orcid.org/0000-0001-7399-4745
José M. Marbán, josemaria.marban@uva.es, https://orcid.org/0000-0002-6561-6784
1 Didáctica de la Matemática, Ciencias Experimentales y Sociales, Universidad del País Vasco/ Euskal Herriko Unibertsitatea, Bilbao, España.
2 Didáctica de las Ciencias Experimentales, Sociales y de la Matemática. Universidad de Valladolid, Valladolid, España.
Adaptation and Validation of a Scale of Self-Regulation of Learning in Mathematical Problem Solving (Josune Landa, Ainhoa Berciano • José M. Marbán) Uniciencia is protected by Attribution-NonCommercial-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0)
URL: www.revistas.una.ac.cr/uniciencia
Correo electrónico: revistauniciencia@una.cr


