Usos de la cuantificación y categoría de modelación. Una transversalidad de conocimiento matemático

Uses of quantification and category of modeling. A transversality of mathematical knowledge

Usos da quantificação e categoria de modelagem. Uma transversalidade do conhecimento matemático

Claudio Gaete-Peralta1*, Francisco Cordero2, Jaime Huincahue3, Jaime Mena4

Received: Sep/13/2023 • Accepted: Feb/15/2024 • Published: Jul/31/2024

Resumen [Objetivo] La enseñanza de la cuantificación suele enfocarse en fórmulas para cuantificar la medida de magnitudes geométricas, ignorando sus usos en otras disciplinas. Esto hace indispensable formular marcos de referencia que le permitan a dicha enseñanza atender las justificaciones funcionales demandadas por otros dominios de conocimiento. Por tal razón, y enmarcada en la socioepistemología, el objetivo de esta investigación fue formular una epistemología de usos de la cuantificación. [Metodología] La metodología fue cualitativa y estuvo conformada por un corpus teórico-metodológico que articuló constructos de la categoría de modelación con datos empíricos. Esta formulación se llevó a cabo en dos fases. En la primera se enunció, de manera hipotética, una epistemología con base en un análisis a la resignificación de usos de la cuantificación construida en dos situaciones específicas de medición: una propia de una comunidad interdisciplinar y otra propia de la obra matemática titulada Intégrale, Longueur, Aire. La segunda fase analizó la emergencia de una resignificación de usos de la cuantificación en estudiantes de ingeniería durante el desarrollo de una situación escolar diseñada con base en la epistemología hipotética. [Resultados] Esta emergencia permitió validar empíricamente esta epistemología y expresar una transversalidad de usos de la cuantificación en situaciones específicas de medición, conformadas de significaciones, procedimientos e instrumentos que en conjunto derivan argumentaciones de cuantificación. [Conclusiones] Esta epistemología de usos permite plasmar a la situación de medición como un referente educativo para establecer el uso, la resignificación y la transversalidad de la cuantificación. Palabras clave: usos de la cuantificación; categoría de modelación; socioepistemología; comunidad interdisciplinar; transversalidad; estudiantes de ingeniería. Abstract [Objective] The teaching of quantification tends to focus on formulas for quantifying the measurement of geometric magnitudes, ignoring their uses in other disciplines. This makes it essential to formulate reference frameworks that allow such teaching to meet the functional justifications demanded by other domains of knowledge. For this reason, and within the framework of socioepistemology, the aim of this research was to formulate an epistemology of the uses of quantification. [Methodology] The methodology was qualitative and consisted of a theoretical-methodological corpus that articulated constructs of a modelling category with empirical data. This formulation was carried out in two phases. In the first one, an epistemology was hypothetically formulated based on an analysis of resignification of the uses of quantification constructed in two specific measurement situations: one specific to an interdisciplinary community, and the other to the mathematical work entitled Intégrale, Longueur, Aire. The second phase analyzed the emergence of a resignification of the uses of quantification by engineering students during the development of a school situation designed on the basis of hypothetical epistemology. [Results] This emergence made it possible to empirically validate this epistemology and to express a transversality of uses of quantification in specific measurement situations, made up of meanings, procedures and instruments that together can be used to derive quantification arguments. [Conclusions] This epistemology of uses makes it possible to capture the measurement situation as an educational reference to establish the use, resignification, and transversality of quantification. Keywords: Uses of quantification; category of modeling; socioepistemology; interdisciplinary community; transversality; engineering students. Resumo [Objetivo] O ensino da quantificação geralmente se concentra em fórmulas para quantificar a medição de magnitude geométricas, ignorando seus usos em outras disciplinas. Isso torna essencial a formulação de estruturas de referência que permitam que esse ensino atenda às justificativas funcionais exigidas por outros domínios do conhecimento. Por esse motivo, e dentro da estrutura da epistemologia social, o objetivo desta pesquisa foi formular uma epistemologia dos usos da quantificação. [Metodologia] A metodologia foi qualitativa e consistiu em um corpus teórico-metodológico que articulou construções da categoria de modelagem com dados empíricos. Essa formulação foi realizada em duas fases. O primeiro enunciou hipoteticamente uma epistemologia baseada em uma análise da ressignificação dos usos da quantificação construída em duas situações específicas de medição: uma específica de uma comunidade interdisciplinar e a outra do trabalho matemático intitulado Intégrale, Longueur, Aire. A segunda fase analisou o surgimento de uma ressignificação dos usos da quantificação em estudantes de engenharia durante o desenvolvimento de uma situação escolar projetada com base na epistemologia hipotética. [Resultados] Esse surgimento permitiu validar empiricamente essa epistemologia e expressar uma transversalidade de usos da quantificação em situações específicas de medição, composta de significados, procedimentos e instrumentos que, juntos, derivam argumentos de quantificação. [Conclusões] Essa epistemologia de usos permite que a situação de medição seja moldada como uma referência educacional para estabelecer o uso, a ressignificação e a transversalidade da quantificação. Palavras-chave: usos da quantificação; categoria de modelagem; epistemologia social; comunidade interdisciplinar; transversalidade; estudantes de engenharia.

Introducción

Un propósito de la enseñanza de la matemática es vincularse con la realidad, para que el estudiantado sea capaz de enfrentar problemas que formen parte de la vida cotidiana (Acebo y Rodríguez, 2019). En esa línea, los estándares educativos de muchos países hacen hincapié en la importancia de acercar las matemáticas escolares a situaciones de la vida real (Larina, 2016). Sin embargo, reconocer conocimientos matemáticos que no están institucionalizados y que son funcionales para la gente resulta complejo para todos los niveles educativos, pues se desconocen los usos de la matemática fuera del aula (Acebo y Rodríguez, 2019). Ante este desconocimiento, la enseñanza de la matemática suele trabajar con tareas estereotipadas, cuyas realidades resultan ser artificiales y aportan poco al logro de este vínculo (Villa-Ochoa, 2015). Además, la concepción cultural de la matemática como una disciplina abstracta e infalible complejiza aún más el logro de este vínculo, pues reconoce a la matemática escolar como algo intacto, en donde la persona se limita a aprender reglas y procedimientos, dejando de lado la funcionalidad del conocimiento matemático (Cordero et al., 2015).

Lo señalado anteriormente motiva a que la educación matemática formule marcos de referencia que le permitan a la matemática escolar dar cuenta del uso de la matemática en la realidad, y así generar un impacto educativo y social en el mundo (Cirillo et al., 2016). Una forma de realizar esto es a través de una perspectiva socioepistemológica (Cantoral, 2013), específicamente en el marco del programa Sujeto Olvidado y Transversalidad de Saberes (SOLTSA), en donde se crean epistemologías de usos para atender las justificaciones funcionales del conocimiento matemático que demandan dominios de conocimiento tales como los disciplinares y los de la vida, con el fin de conformar elementos de diálogo entre la matemática escolar y el quehacer cotidiano de la gente.

La justificación funcional plantea que los mecanismos en los cuales se desarrollan los usos de conocimiento matemático en situaciones específicas son funcionales; es decir, lo que norma la justificación le da utilidad a lo humano (Cordero y Flores, 2007). La formulación de estas epistemologías se realiza con base en un desarrollo de la categoría de modelación (Cordero et al., 2022), la cual impulsa un estudio sobre la construcción social de conocimiento matemático para dar cuenta de dos aspectos: la pluralidad epistemológica y la transversalidad de usos del conocimiento matemático (Cordero, 2016). Estos permiten confrontar los tratamientos escolares habituales para abrir un tratamiento alternativo que favorezca el aprendizaje de los significados de la matemática (Cordero y Solís, 2022).

La particularidad de esta investigación consiste en haber identificado elementos para formular una epistemología de usos de la cuantificación. La construcción de estos marcos de referencia son una condición sine qua non para crear el diálogo entre la matemática escolar y el cotidiano disciplinar de otros dominios de conocimiento (Cordero, 2016).

Antecedentes y problemática

La cuantificación constituye el núcleo del hacer matemáticas en la vida cotidiana (Saxe, 2004) y es un método primario ampliamente utilizado para describir y medir diferentes tipos de atributos de los aspectos del mundo (OCDE, 2017).

En términos educativos, y en concordancia con García (2018), en clases de matemática generalmente la enseñanza de la cuantificación se reduce a cuantificar realidades sin escenarios socioculturales. Al respecto, la Organización para la Cooperación y el Desarrollo Económicos (OCDE) consideró a la cuantificación de medidas de magnitudes geométricas como una de las temáticas que forma parte de la prueba internacional PISA-D de matemáticas, en donde la medida de ángulos, distancias, longitudes, perímetros, áreas y volúmenes son parte de los contenidos a evaluar en esta prueba.

En el caso particular de Chile, este tipo de cuantificación conforman las bases curriculares del Ministerio de Educación (MINEDUC) de primero a sexto básico (MINEDUC, 2018), las cuales buscan que el alumnado cuantifique magnitudes tales como ancho, largo, alto, peso, área, volumen, entre otros, marcando una fuerte tendencia por llevar la enseñanza de la cuantificación a contextos propios de la Geometría. Desde séptimo básico a tercero medio, las bases curriculares (MINEDUC, 2015) hacen explícita dicha tendencia al contemplar un eje temático de Geometría, el cual establece objetivos de aprendizaje cuyo propósito es lograr que el estudiantado cuantifique la medida de ángulos, así como perímetros, áreas y volúmenes de diferentes figuras geométricas.

Con esos lineamientos, los textos escolares oficiales de matemática del MINEDUC de séptimo a tercero medio (p.e. Iturra et al., 2022; Torres y Caroca, 2022; Fresno, Torres y Ávila, 2022; Díaz et al., 2020; Osorio et al., 2019) proponen diferentes tipos de actividades para que el alumnado cuantifique, a través del uso de fórmulas, la medida de ángulos inscritos en polígonos, perímetros de circunferencias, áreas de paralelogramos, triángulos, trapecios y círculos, volúmenes de prismas, cilindros, conos y esferas y la longitud de cuerdas y arcos, entre otros.

Lo anterior identifica en la Geometría a referentes de la matemática escolar para llevar a cabo la enseñanza de la cuantificación, en donde se pretende que el estudiantado aplique diferentes fórmulas para cuantificar medidas de una amplia variedad de magnitudes geométricas. Esto da lugar a una falta de marcos de referencia para la matemática escolar que permitan valorar los usos de la cuantificación que ocurren en situaciones cotidianas de la gente y atender las justificaciones funcionales demandadas por otros dominios de conocimiento.

Con el propósito de abordar esta problemática, el objetivo de esta investigación fue formular una epistemología de usos de la cuantificación. Para dicho fin, el artículo se estructura de la siguiente manera: en primer lugar, se dará a conocer el marco teórico que sustentó esta investigación, en donde se profundiza respecto al programa SOLTSA, las epistemologías de usos, la categoría de modelación y su rol en la formulación de estas epistemologías. En segundo, se mostrará la metodología que permitió responder al objetivo de investigación. En tercer lugar, se dará cuenta del análisis y los resultados de investigación. Y en cuarto y último lugar, se reportarán las discusiones y conclusiones de este estudio.

Marco teórico

La socioepistemología busca explicar el enigma de la construcción social de conocimiento matemático y su difusión institucional (Cantoral, 2013). Un constructo medular es la práctica social, entendida como un sistema complejo de procesos de dimensión social en el que se problematiza el saber matemático al confrontar los saberes sabio, técnico y popular para sintetizarlos en la sabiduría humana (Cordero et al., 2019). Esta teoría promueve una descentración de los objetos matemáticos y prioriza la forma en cómo la gente hace uso del conocimiento matemático (𝒰(CM)) en situaciones que forman parte de su cotidiano (Cordero et al., 2019).

Para abordar el objetivo planteado, esta investigación se situó dentro del programa SOLTSA, cuyo fin principal consiste en revelar los 𝒰(CM) y sus resignificaciones que emergen en comunidades de conocimiento matemático (CCM) en diferentes escenarios: la escuela, el trabajo y la ciudad (Cordero et al., 2022). Para este programa, la matemática escolar es de naturaleza dual; es decir, en algunas ocasiones su objeto de estudio es la matemática, donde imperan justificaciones razonadas, entendidas como aquellas justificaciones que permiten construir conocimiento matemático desde la misma estructura matemática (Cordero et al., 2015). En otras es la matemática como instrumento para otros dominios de conocimiento, donde imperan justificaciones funcionales. Las dos líneas de trabajo que desarrolla SOLTSA actúan de manera simultánea: la resignificación del conocimiento matemático y su impacto educativo. En la primera línea se problematizan las categorías de conocimiento matemático que suceden en las CCM entre diferentes dominios de conocimiento: el discurso matemático escolar, el campo disciplinar y el cotidiano de la comunidad.

Las categorías de conocimiento matemático son prácticas plasmadas como la argumentación de una situación específica (Cordero, 2016), entendiendo argumentación como el “hilo conductor de la situación específica de donde emergen los conocimientos matemáticos” (Cordero et al., 2015, p. 74). Dentro de las categorías reportadas en investigaciones socioepistemológicas se pueden mencionar la predicción, el comportamiento tendencial, la analiticidad de las funciones (Cordero, 2008), la optimización (Cordero et al., 2019), la compensación (Medina, 2019) y la anticipación (Pérez-Oxté, 2021). Estas categorías son un conocimiento distinto al centrado en el objeto matemático y su desarrollo en la matemática escolar favorece la descentración (Mendoza y Cordero, 2018). Por ejemplo, desarrollar la categoría de optimización en la matemática escolar contribuye a descentrar los objetos matemáticos presentes en métodos como la programación lineal y los multiplicadores de Lagrange (Cordero et al., 2019). En la segunda línea de trabajo se conforman los multifactores y estadios que coadyuvan a conformar programas de acompañamiento permanentes entre el profesorado de matemáticas (Cordero et al., 2022).

La categoría de modelación

La categoría de modelación, ζ(Mod), es una variedad de modelación matemática abordada desde la socioepistemología cuyo principio P´ valora la matemática funcional de la gente en la relación recíproca y horizontal entre la matemática escolar y el cotidiano, donde “la relación recíproca es el indicador de que la matemática escolar y la matemática de la vida deben afectarse mutuamente, mientras que la relación horizontal es el indicador de que deben conservar el mismo estatus y valor epistemológico” (Mendoza y Cordero, 2018, p. 44). Este principio no permite una separación entre la matemática y la realidad, en contraparte de otras posturas teóricas de modelación que ofrecen alternativas para relacionarlas.

Ahora bien, la ζ(Mod) legitima los 𝒰(CM) que ocurren en diferentes dominios de conocimiento, así como en la alternancia de estos, entendiendo por 𝒰(CM) como las funciones orgánicas de las situaciones (funcionamientos), las cuales se manifiestan por las “tareas” que componen la situación y las formas del uso relacionadas a la clase de esas “tareas”. En cuanto a las tareas, estas pueden ser actividades, acciones, ejecuciones o alternancias de dominios propias del organismo de la situación (Cordero et al., 2022). El binomio funcionamiento-forma es utilizado para caracterizar a los 𝒰(CM), donde “el funcionamiento es la función-utilidad que tiene el conocimiento matemático en una situación específica y la forma es la generalización del tipo de acciones que se realizan dentro de esta” (Morales, 2020, p. 35).

La Figura 1 representa un esquema de la ζ(Mod) y estructura los elementos que permiten promover una movilidad de usos y significados del conocimiento matemático, los cuales emergen de CCM en situaciones específicas Sin, y podrían estar sobre escenarios o dominios de conocimiento Dn. Estas se componen de elementos que construyen conocimiento matemático: significaciones, procedimientos e instrumento, y estos en conjunto derivan la argumentación de Sin, la cual corresponde a una resignificación de 𝒰(CM), Re(𝒰(CM)), construida por la CCM en Sin.

Una Re(𝒰(CM)) se refiere a una epistemología de 𝒰(CM) que en el contexto de la matemática escolar es inusual; pues se refiere a una matemática en forma de procesos permanentes (usos y significados) que emergen de las CCM, en contraparte de objetos terminales (conceptos y definiciones), los cuales no necesariamente surgen en los sujetos (Cordero et al., 2019).

De lo anterior, se desprende la naturaleza empírica de una epistemología de 𝒰(CM). Estas son bases epistemológicas para el diseño de situaciones escolares de socialización (DSES) capaces de favorecer a los 𝒰(CM), en contraparte de otros tipos de diseños que promueven la emulación de un concepto (Morales, 2020). Además, estas epistemologías conforman la Socioepistemología del Cálculo y el Análisis (Figura 11) y su formulación es uno de los propósitos del programa SOLTSA.

La relación entre Sin y Dn se ve afectada por un eje Er, el cual singulariza epistemológicamente la actividad matemática ocurrida en Sin. Esta singularidad ha sido reportada en diferentes investigaciones, como es el caso de la selección en el dominio de la ingeniería mecatrónica (Cordero et al., 2019) o en el de una situación de periodización en el dominio de la ingeniería química (Pérez-Oxté, 2021), entre otras. La ζ(Mod) valora las transversalidades del conocimiento matemático, entendidas como las Re(𝒰(CM)) entre escenarios o dominios Dn (por ejemplo, entre la escuela y el trabajo; o entre la matemática y la ingeniería). Estas transversalidades suceden en momentos (Moi), los cuales son fases del proceso situacional (Mendoza y Cordero, 2018). Adicionalmente, la ζ(Mod) valora la institucionalización; es decir, se reconoce que el conocimiento matemático posee su propia estructura de validación, la cual depende de la CCM en cuestión.

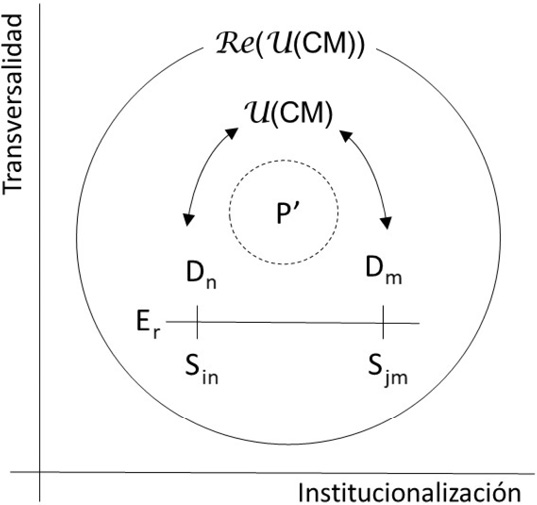
Figura 1. La Categoría de Modelación

Fuente: Cordero et al. (2022).

Un ejemplo de formulación de una epistemología de 𝒰(CM) con base en el desarrollo de la ζ(Mod) lo plantea Cordero et al. (2019) al analizar la resignificación de usos de la optimización en tres situaciones de selección: una propia de la obra de Lagrange, titulada Mécanique Analytique; otra de la ingeniería mecatrónica y la última de un escenario escolar con ingenieros en formación. Los resultados mostraron que estos usos también se resignificaron en las transversalidades entre estos escenarios, los cuales sucedieron en tres momentos: la ecuación de equilibrio, la calidad de imagen y el comportamiento estable. Esto permitió formular una epistemología capaz de expresar una transversalidad de usos en situaciones específicas de selección, conformadas por elementos que en conjunto derivan en argumentaciones de optimización: lo estable como instrumento, la distinción de cualidades como procedimiento y los patrones de adaptación como significación. Esta epistemología cristaliza la selección como “una referencia para establecer el uso, la resignificación y transversalidad de la optimización” (Cordero et al., 2019, p. 194).

Con base en un desarrollo de la ζ(Mod), este estudio analizó la resignificación de usos de la cuantificación en tres situaciones de medición: una propia de una comunidad interdisciplinar, otra de la obra matemática de Lebesgue (1902) y la última de un escenario escolar con estudiantes de ingeniería. El análisis de estas tres situaciones permitió formular una epistemología capaz de transmitir la transversalidad de usos de la cuantificación en situaciones de medición, las cuales se conforman de elementos que en conjunto derivan argumentaciones de cuantificación: lo medible como instrumento, la clasificación como procedimiento y la medida de magnitudes como significación.

Metodología

Ubicada en un paradigma interpretativo, esta investigación utilizó una metodología cualitativa conformada por un corpus teórico-metodológico que articuló constructos teóricos de la ζ(Mod) con datos empíricos. Para ello, y en concordancia con lo realizado por diferentes investigaciones socioepistemológicas (p. e. Cordero et al., 2019 y Marcía, 2020), la formulación de la epistemología de usos de la cuantificación se realizó en dos fases, las cuales se detallan a continuación.

Fase 1. Formulación de una epistemología de usos hipotética. En esta primera fase se planteó, de manera teórica, una epistemología de usos. Debido a su naturaleza empírica, esta fue considerada hipotética.

Una epistemología de usos debe dar cuenta de la naturaleza dual de la matemática. Por tal motivo, la formulación de esta epistemología hipotética se realizó a partir de un análisis a la resignificación de usos construida en dos situaciones específicas: una normada por una justificación funcional y otra por una justificación razonada. En particular, se investigó la resignificación de usos de la cuantificación construida en dos situaciones de medición: una propia de una CCM interdisciplinar y otra propia de la obra de Lebesgue (1902). La escogencia de estas situaciones se debió a que la cuantificación (de Unidades Formadoras de Colonias y de la medida de un subconjunto específico de ℝ2, respectivamente) fue una argumentación que permitió la emergencia de conocimiento matemático. Estos análisis permitieron formular, de manera teórica, una epistemología de usos compuesta por significaciones, procedimientos, instrumento y argumentación, la cual expresó una transversalidad de usos de la cuantificación entre ambas situaciones.

Fase 2. Emergencia de una resignificación de usos de la cuantificación. En esta fase se involucró a estudiantes de ingeniería con un DSES basado en la epistemología hipotética. La emergencia de una resignificación de usos de la cuantificación por parte del estudiantado tras desarrollar esta situación le otorgó una naturaleza empírica a la epistemología de usos.

Recolección y análisis de datos

A continuación, se dará cuenta de la recolección y el análisis de datos que fue realizada en cada una de las fases planteadas.

Recolección y análisis de datos para la fase 1

En el caso de la CCM, se realizó una inmersión con una comunidad de profesionales que participaron de un proyecto cuyo objetivo consisitió en validar in situ las propiedades antibacterianas de un recubrimiento aplicado en un calabozo de una comisaría de carabineros de Chile (policía nacional). El grupo lo conformaron una ingeniera civil química con un doctorado en Ciencias de la Ingeniería, mención en Ciencia de los Materiales (P1); un ingeniero químico (P2), un químico con un doctorado en Química (P3), un bioquímico con un doctorado en Biotecnología (P4) y un estadístico con un Magíster en Estadística (P5). Este proyecto se desarrolló en cinco etapas consecutivas: Etapa 1: Preparación de un recubrimiento antimicrobiano, Etapa 2: Aplicación del recubrimiento, Etapa 3: Toma de muestras de bacterias coliformes, Etapa 4: Cuantificación de bacterias coliformes y Etapa 5: Validación de propiedades antimicrobianas.

Para la investigación, esta comunidad fue considerada interdisciplinar, pues este concepto fue entendido como un proceso que integra “información, datos, métodos, herramientas, conceptos y/o teorías de dos o más disciplinas centradas en una pregunta compleja, problema, tópico o tema” (Peek y Guikema, 2021). En este caso, la realización del proyecto necesitó integrar conocimientos y métodos de Ciencia de los Materiales (con base en Ingeniería Química), Química, Microbiología y Estadística. Además, las integraciones se realizaron a través de dos tipos de diálogos interdisciplinares, los cuales esta investigación define como cruzamiento y secuencialidad convergente. El primero ocurre cuando las disciplinas involucradas ofrecen ópticas cruzadas dentro de un problema, dando ideas y desarrollos para entregar una respuesta que no es propia de ninguna de las disciplinas involucradas, sino del resultado del cruce de ópticas de cada una. La segunda sucede cuando el problema es atendido inicialmente por una disciplina, la cual obtiene resultados parciales que le permiten a la otra disciplina continuar con el problema y ofrecer una solución que no haya sido posible de encontrar solo por una disciplina. La Tabla 1 muestra la integración de conocimientos, métodos y tipos de diálogos interdisciplinarios para cada una de las etapas.

Tabla 1. Conocimientos, métodos y diálogos interdisciplinarios para cada etapa del proyecto

Etapas	Disciplinas involucradas	Conocimientos o métodos integrados	Tipo de diálogo interdisciplinar
1	Ciencia de los materiales y Química	Los conocimientos de ciencia de los materiales fueron necesarios para determinar el porcentaje de mezcla del aditivo con la pintura y los métodos de la química se requirieron para realizar la preparación del recubrimiento.	Secuencialidad convergente.
2	Ciencia de los materiales y Microbiología	Se necesitaron métodos de ciencias de los materiales para aplicar de manera correcta el recubrimiento en el calabozo y de conocimientos de la microbiología para determinar en qué partes del calabozo debía aplicarse el recubrimiento.	Cruzamiento convergente.
3	Microbiología	Se necesitaron métodos de la microbiología para realizar la recolección de muestras de manera correcta.	No aplica por haber una sola disciplina involucrada.
4	Microbiología	Se necesitaron métodos de la microbiología para realizar la cuantificación de bacterias coliformes.	No aplica, por haber una sola disciplina involucrada.
5	Estadística y Ciencia de los materiales	Se necesitaron métodos estadísticos para llevar a cabo la validación de propiedades antibacterianas y de conocimientos de la ciencia de los materiales para la interpretación de los resultados obtenidos respecto del objetivo del proyecto.	Cruzamiento convergente.

Nota: fuente propia de la investigación.

La inmersión tuvo una duración de tres meses. Se recolectaron datos por medio de (a) registros audiovisuales y fotográficos para apoyar la observación realizada por las personas investigadoras y (b) entrevistas semiestructuradas a las personas profesionales de esta comunidad para comprender de mejor manera aspectos relacionados con el desarrollo del proyecto. Los datos recolectados fueron transcritos para su posterior análisis.

Además, para evitar introducir posibles obstáculos a la objetividad de los datos recolectados a través de una participación de las personas investigadoras en esta comunidad, se optó por hacer que el rol de investigadores(as) fuese el de observadores(as) (Holy, 1984). Esto permitió identificar la situación de medición en donde la comunidad hizo uso de la cuantificación y con constructos teóricos de la ζ(Mod) y técnicas de análisis documental (Rojas, 2011) se analizó la resignificación de usos construida por esta comunidad en dicha situación.

Para la obra matemática, se eligió la obra Intégrale, Longueur, Aire (Lebesgue, 1902), la cual construyó la integral definida a partir de la medida de un conjunto. Para una mayor comprensión de esta obra, se recurrió a otros textos contemporáneos que permitieron una interiorización, tanto del contexto histórico, como de las motivaciones y propósitos de Lebesgue para realizar su creación. Las obras elegidas fueron Cauchy (1823), Dirichlet (1829), Riemann (1867), Jordan (1892) y Borel (1898). A partir de un análisis documental (Rojas, 2011) se identificó la situación de medición donde Lebesgue hizo uso de la cuantificación, y con constructos teóricos de la ζ(Mod) y técnicas de análisis documental (Rojas, 2011), se analizó la resignificación de usos de la cuantificación construida en este contexto.

Los usos de la cuantificación, en la comunidad interdisciplinar y en la obra de Lebesgue (1902), se analizaron mediante un debate entre funcionamiento y forma, donde el primero responde a para qué es usado el conocimiento y el segundo a cómo es usado el conocimiento (Parra y Méndez, 2021). Cabe señalar que este análisis de 𝒰(CM) ha sido realizado en distintos trabajos socioepistemológicos (p. e. Cordero et al., 2019).

Recolección y análisis de datos para la fase 2

La epistemología hipotética sirvió de base para construir un DSES (Figura 7), que permitió analizar la resignificación de usos de la cuantificación construida por el estudiantado tras desarrollar la situación (el detalle sobre cómo fue realizado el DSES se encuentra en la subsección Emergencia de una resignificación de usos de la cuantificación en estudiantes). Para este propósito se realizó un estudio de caso (Stake, 1995) con doce estudiantes de ingeniería de una universidad chilena (rotulados como E1, E2,.., E12), para describir e interpretar las racionalidades y sus formas de interactuar durante el desarrollo de la situación. Se les pidió a las personas participantes trabajar en grupos para fomentar el trabajo colaborativo. Además, accedieron a participar voluntariamente y completaron un un consentimiento informado, pudiendo dejar de participar en el proceso en cualquier momento.

Los datos se recolectaron por medio de notas de campo y registros escritos y audiovisuales de las producciones de las personas participantes. Con constructos teóricos de la ζ(Mod) y técnicas interpretativas del análisis del contenido (Flick, 2004), se analizó la resignificación de usos de la cuantificación construida. Finalmente, los usos de la cuantificación fueron analizados por medio de un debate entre funcionamiento y forma.

Análisis y resultados

Resignificación de usos de la cuantificación en una comunidad interdisciplinar

La contaminación de microorganismos produce problemas asociados a la transmisión de enfermedades o al deterioro de superficies a las cuales estos se adhieren (Delgado, 2013). Con el fin de confrontar este problema, Delgado (2013) desarrolló un aditivo (Figura 2) para elaborar recubrimientos superficiales como medida complementaria y prevenir enfermedades como aquellas provocadas por bacterias coliformes.

Figura 2. Aditivo utilizado para elaborar recubrimientos

Nota: fuente propia de la investigación.

Para probar la potencialidad del aditivo, esta comunidad participó en un proyecto que buscó determinar si un recubrimiento elaborado con base en ese aditivo reducía significativamente la cantidad de bacterias coliformes en un calabozo. A continuación, se detallará cada una de las etapas que permitieron, de manera consecutiva, desarrollar este proyecto.

Etapa 1. Preparación de un recubrimiento antimicrobiano. La preparación del recubrimiento consideró lo indicado por P1 durante las entrevistas: un kilógramo de recubrimiento debía conformarse por 95 % de pintura al óleo y 5 % de aditivo. Con base en esto, P2 elaboró el recubrimiento con 20 litros de pintura utilizando un recipiente de vidrio graduado que le facilitó sacar pintura en menor volumen (800 ml) para manipularla de forma cómoda, según lo señalado por él en las entrevistas. Para preparar 800 ml de recubrimiento, la homogeneización de la mezcla primero se hizo manualmente y luego con agitadores mecánicos. Durante esta etapa, P1 y P2 dialogaron constantemente para que la preparación del recubrimiento fuese segura (evitar el esparcimiento en el aire de partículas tóxicas) y óptima (perder la menor cantidad posible de aditivo).

Etapa 2. Aplicación del recubrimiento. Una vez preparado el recubrimiento, P2 y carabineros pintaron el cielo, los muros, el asiento, el piso y los barrotes de uno de los calabozos. Durante las entrevistas, P1 y P4 señalaron que decidieron aplicar el recubrimiento en todo el calabozo para evitar sesgos en la carga bacteriana. Por otra parte, P1 entregó indicaciones para no aplicar más de una capa de recubrimiento, la cual debía ser lo más homogénea posible para evitar que algunos sectores del calabozo tuviesen mayor carga antimicrobiana.

Etapa 3. Toma de muestras de bacterias coliformes. Una semana después, se inició la toma de muestras de bacterias coliformes en ocho zonas específicas del calabozo. Durante las entrevistas, la comunidad señaló que estas zonas fueron elegidas con base en lo que carabineros consideró, por experiencia, eran las zonas de mayor contacto de las personas detenidas con el calabozo: dos zonas de la banca, dos zonas en uno de los muros, dos zonas en el piso, una zona de la reja y la manilla de la reja (Figura 3).

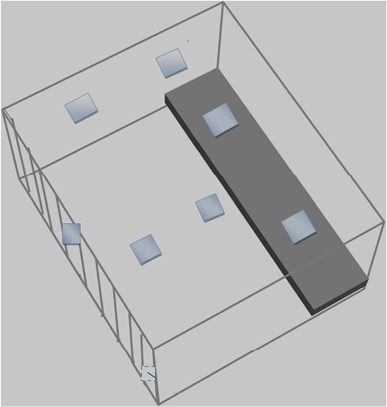
Figura 3. Zonas de mayor contacto con el calabozo

Nota: fuente propia de la investigación.

Para tomar muestras se utilizaron microsnaps, pruebas que permitieron detectar y cuantificar bacterias viables, bacterias capaces de crecer y formar colonias en medios de cultivo específicos (Paraje y Tamagnini, 2015). Los microsnaps fueron de dos tipos: incubación y detección. El primero contuvo un medio de cultivo que al reaccionar con las muestras provocó la generación de colonias. El microsnap de detección permitió cuantificar la cantidad de luz emitida tras la reacción del sustrato incorporado en este dispositivo con moléculas de Adenosín Trifosfato (ATP) de las bacterias. La cantidad de luz se cuantificó con un luminómetro (Figura 4) y fue medida en Unidades Relativas de Luz (URL).

Durante las entrevistas, la comunidad señaló que la cantidad de URL es directamente proporcional a la concentración de ATP presente en las bacterias y, a su vez, esta última es proporcional a la cantidad de UFC de la muestra incubada.

Figura 4. Luminómetro utilizado para cuantificar la señal de luz

Nota: fuente propia de la investigación.

La toma de muestras se realizó con microsnaps de incubación (Figura 5). Luego, las muestras recolectadas fueron guardadas en un recipiente para mantenerlas a temperaturas entre 0 °C y 10 °C durante 48 horas. La comunidad entrevistada señaló que esto se hizo para evitar que las muestras recolectadas murieran.

Figura 5. Toma de muestras de bacterias coliformes

Nota: fuente propia de la investigación.

Etapa 4. Cuantificación de bacterias coliformes. Para cuantificar las UFC, se utilizaron dos equipos: una incubadora y un luminómetro. Primero, se rompió una válvula en los microsnaps de incubación para liberar un sustrato que reaccionó con las muestras recolectadas. Luego, y con el propósito de proliferar el crecimiento bacteriano, las muestras que reaccionaron con el sustrato se colocaron en una incubadora durante siete horas a una temperatura de 37 °C. Faltando cinco minutos para terminar la incubación, los microsnaps de detección se ubicaron en la incubadora para calentar el sustrato bioluminogénico contenido en cada uno de uno. Pasado los cinco minutos, se hicieron reaccionar las muestras con crecimiento bacteriano con este sustrato para cuantificar las URL.

La Tabla 2a muestra la relación entre la cantidad de UFC y de URL, validado por la AOAC Research Institute (Hygiena, s. f.). Esto sirvió de base para que la comunidad cuantificara las UFC a través de una conversión de URL a UFC por una regla de tres (Tabla 2b).

Tabla 2a. Relación entre URL y UFC

UFC estimadas	URL en luminómetro
< 10	< 2
< 20	< 4
< 50	< 7
< 100	< 12
< 200	< 20
< 500	< 35
< 1.000	< 60
< 5.000	< 180
< 10.000	< 300

Nota: fuente propia de la investigación.

Tabla 2b. Conversión de URL a UFC

Número de URL (N)	Conversión a UFC
0 ≤ N ≤ 4	1 URL = 5 UFC
4 < N ≤ 7	1 URL = 7,14 UFC
7 < N ≤ 12	1 URL = 8,33 UFC
12 < N ≤ 20	1 URL = 10 UFC
20 < N ≤ 35	1 URL = 14,28 UFC
35 < N ≤ 60	1 URL = 16,67 UFC
60 < N ≤ 180	1 URL = 27,78 UFC
180 < N ≤ 300	1 URL = 33,33 UFC

Nota: fuente propia de la investigación.

Esta conversión permitió cuantificar las UFC para evaluar el efecto antimicrobiano del recubrimiento a lo largo del tiempo (por lo tanto, el calabozo se ocupó y desocupó constantemente y cada vez que estuvo desocupado se tomaron muestras). La Figura 6 indica la cantidad de UFC en estas zonas durante distintas fechas, donde las abreviaciones fueron: M1 (Muestra 1), M2 (Muestra 2), As1 (zona específica 1 del asiento), As2 (zona específica 2 del asiento), Mr1 (zona específica 1 del muro), Mr2 (zona específica 2 del muro), P1 (zona específica 1 del piso), P2 (zona específica 2 del piso), R1 (zona específica de la reja) y R2 (manilla de la reja). Como ejemplo, la muestra 2 de la zona Mr2, tomada el 12 de octubre de 2022, marcó 5 URL, equivalente a 5 · 7,14 = 35,7 UFC .

Respecto al uso de la cuantificación en esta etapa, su funcionamiento fue para determinar las UFC en las muestras recolectadas y su forma fue a través de una conversión de URL a UFC por medio de una regla de tres.

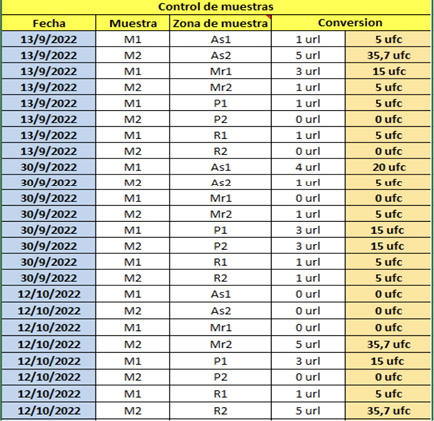
Figura 6. Cuantificación de UFC en zonas del calabozo

Nota: fuente propia de la investigación.

Etapa 5. Validación de propiedades antimicrobianas. En esta etapa se realizó un análisis estadístico a los datos provenientes de las UFC de las muestras recolectadas, para validar las propiedades antibacterianas del recubrimiento. En esta etapa, el diálogo entre P1 y P5 permitió interpretar de mejor manera los resultados obtenidos respecto al objetivo del proyecto.

Durante la etapa 4 emergió una situación de medición que calculó la cantidad de bacterias coliformes en las muestras recolectadas. La argumentación vino dada por una cuantificación de UFC, en donde la viabilidad de estas bacterias fue necesaria para que crecieran y formaran colonias en medios de cultivo específicos. De esta forma, lo medible de la cantidad de bacterias coliformes, dado por su viabilidad, fue un instrumento que le permitió al grupo realizar un procedimiento de clasificación según su cantidad de URL, permitiendo, por medio de una regla de tres, cuantificar las UFC en cada muestra. Lo anterior le otorgó al conocimiento matemático un significado asociado a la medida de la cantidad de bacterias coliformes, expresada en UFC.

En términos de los constructos teóricos de la ζ(Mod), una significación asociada a la medida de la cantidad de bacterias coliformes, un procedimiento de clasificación y lo medible como instrumento derivaron una argumentación de cuantificación, la cual corresponde a una resignificación de usos construida por la comunidad en esta situación de medición.

Resignificación de usos de la cuantificación en la obra de Lebesgue

Para Canela (2016), durante el siglo XIX se produjo un proceso de aritmetización del análisis matemático que pretendía dejar atrás la intuición geométrica, característica del siglo XVIII, que, aunque eficaz, prestaba poca atención al fundamento y a la estructura del análisis como tal. Cauchy (1823), desprendiéndose de la geometría y dando un tratamiento analítico, construyó la integral definida para funciones continuas y posteriormente la extendió a funciones con finitas discontinuidades. Por su parte, Dirichlet (1829) amplió esta construcción a funciones con infinitas discontinuidades, y estableció que este tipo de funciones es integrable si el conjunto de discontinuidades es diseminado (denso en ninguna parte). Riemann (1867) amplió la construcción de este concepto a funciones discontinuas en un conjunto denso de puntos, estableciendo criterios para que una función fuese integrable. Jordan (1892), mediante el concepto de contenido de un conjunto, estudió el conjunto de discontinuidades de una función para construir la integral definida, introduciendo por primera vez una noción de medida en la teoría de integración. Por otra parte, Borel (1898) desarrolló un concepto de medida en términos de recubrimientos infinitos, aunque sin vincular esta idea a la integral definida.

Lo realizado por Jordan y Borel fue base para que Lebesgue iniciara la construcción de una teoría de la medida que cambió la visión topológica presente hasta ese entonces en la construcción de la integral definida. En el primer capítulo de su obra, Lebesgue buscó definir una función medida m, que tomase valores en [0,∞], con las siguientes propiedades:

L1. m(E) ≠ 0, para algún E.

L2. Dos conjuntos iguales tienen la misma medida.

L3. La medida de la unión de un número finito o infinito numerable de conjuntos disjuntos entre sí es la suma de la medida de estos conjuntos.

Para esto, Lebesgue definió la medida de un subconjunto acotado E de ℝ. Para tal propósito, definió la medida exterior de E como

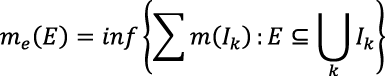
Donde Ik son intervalos de ℝ y m(Ik) corresponde al largo de Ik. Para definir la medida interior de E, al ser un conjunto acotado, se puede suponer que para algún intervalo Ik, E ⊆ Ik. Si se denota por C(E) = Ik — E, entonces la medida interior de E, mi (E), fue definida como

mi (E) = m (Ik) – me (E)

Con base en lo anterior, Lebesgue estableció que un subconjunto acotado E de ℝ es medible, si me (E) = mi (E) y el valor común corresponde a la medida de E, m(E). Además, Lebesgue probó que esta cumple con las condiciones L1, L2 y L3. Para determinar la medida de un subconjunto acotado E de ℝ2, Lebesgue definió la medida exterior de E como:

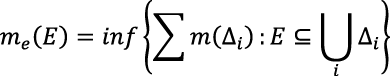
donde ∆i son triángulos del plano y m(∆i) es la medida de Lebesgue del conjunto de puntos de un triángulo, el cual coincide con su área. Por otro lado, Lebesgue definió la medida interior de E, como:

mi (E) = m (ABC) – me(CABC (E)

donde ABC es un triángulo que contiene a E y (CABC (E) corresponde a la medida exterior del complemento de E con respecto al triángulo ABC. De esta manera, E es medible si me(E) = mi(E)y el valor común es la medida de E, m(E). Además, Lebesgue probó que esta también cumple con las condiciones L1, L2 y L3.

Una vez definida la medida para subconjuntos de ℝ y ℝ2, Lebesgue planteó el problema de la integral definida de una función positiva ƒ: [𝛼, 𝛽] → [a, b] desde una perspectiva geométrica, en donde consideró 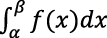como la medida de E = {(x, y) ∈ ℝ2: 0≤ y ≤ ƒ (𝑥), 𝛼 ≤ 𝑥 ≤ 𝛽 }. Sin embargo, E no necesariamente es medible, por lo que Lebesgue necesitó considerar funciones ƒ que permitieran que ese conjunto lo fuese. A este tipo de funciones Lebesgue las denominó sumables. Para construir analíticamente la integral definida de una función ƒ: [𝛼, 𝛽] → [a, b] positiva y sumable, Lebesgue particionó el intervalo [a, b] como a = a0 < a1 < … < an= b y clasificó el dominio de ƒ como:

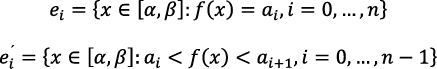
para considerar las sumas

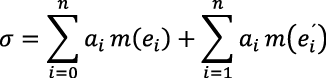
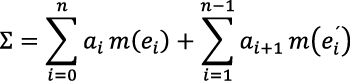
Lebesgue estableció que 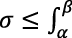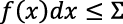, y que 𝜎 y 𝛴 tienen el mismo límite cuando la norma de la partición de [a, b] tiende a cero (denotado como |P| → 0). Dicho valor común corresponde al de 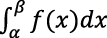. Cabe destacar que Lebesgue demostró que la condición de que ƒ sea sumable es equivalente a que ei y éi son medibles, dándole así sentido a las sumas 𝜎 y 𝛴.

Respecto al uso de la cuantificación ocurrida en esta situación, su funcionamiento fue para determinar la medida de ei y éi, mientras que su forma fue a través de la medida m definida por Lebesgue para subconjuntos de ℝ.

Esta situación específica corresponde a una de medición, pues buscó calcular la medida del conjunto E = {(𝑥, y) ∈ ℝ2: 0 ≤ y ≤ ƒ (𝑥), 𝛼 ≤ 𝑥 ≤ 𝛽}. La argumentación vino dada por la cuantificación de 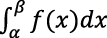, en donde se tornó necesario que ƒ fuese sumable para que E fuera medible. De esta forma, lo medible de E, dado por la condición de que ƒ que sea sumable, fue un instrumento para realizar un procedimiento de clasificación en [𝛼, 𝛽] en los conjuntos ei y éi, lo cual facilitó cuantificar la integral definida, como

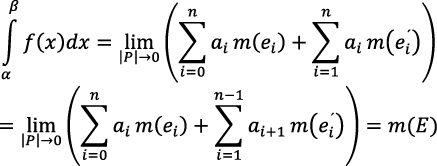
cuyo significado se asoció a la medida de E. En términos de la ζ(Mod), una significación asociada a la medida E, un procedimiento de clasificación y un instrumento ligado a lo medible derivaron una argumentación de cuantificación, la cual corresponde a una resignificación de usos construida por Lebesgue en esta situación de medición.

Una transversalidad de usos de la cuantificación entre dominios de conocimiento

Se entiende por magnitud a aquello que se puede medir y por cuantificación a la expresión numérica de la medida de una magnitud. En el caso de esta investigación, la cantidad de bacterias coliformes viables fue una magnitud medida a través de una cuantificación de UFC, mientras que en Lebesgue (1902), el conjunto E correspondió a una magnitud medida a través de una cuantificación de la integral definida de una función positiva y sumable. Esto, junto con el análisis de la resignificación de usos de la cuantificación construida en los escenarios de la comunidad interdisciplinar y en la obra de Lebesgue (1902), permite inferir teóricamente que dichos usos se resignifican en las transversalidades entre estos escenarios.

Dicha transversalidad se expresa a través de una epistemología de usos según la cual, en situaciones específicas de medición, las significaciones asociadas a la medida de magnitudes, los procedimientos de clasificación e instrumentos ligados a lo medible derivan en argumentaciones de cuantificación. Esta es una epistemología de usos hipotética cuya naturaleza empírica se analiza en la siguiente sección.

Emergencia de una resignificación de usos de la cuantificación en estudiantes

En esta sección se implementó un DSES con estudiantes de ingeniería (Figura 7), para analizar la resignificación de usos de la cuantificación construida. El DSES se realizó con base en la epistemología de usos hipotética y consistió en una situación de medición de una superficie plana, dibujada sobre una cuadrícula, que representó la vista aérea de una laguna. Por su parte, la argumentación de esta situación fue la cuantificación del área de dicha superficie, para determinar si esta laguna corría o no el riesgo de secarse. Para realizar la cuantificación, el grupo de estudiantes debía formular lo medible, es decir, establecer que el área de cada cuadrado de la cuadrícula es de 10.000 mts2 y posteriormente clasificar estos cuadrados en aquellos ubicados al interior de la superficie y aquellos ubicados en su frontera, con el fin de facilitar el cálculo del área de la superficie. En ese sentido, el rol de la cuadrícula fue hacer emerger en los y las estudiantes lo medible como instrumento y la clasificación como procedimiento.

Figura 7. DSES basado en la epistemología hipotética

Nota: fuente propia de la investigación.

Al analizar las producciones del grupo de estudiantes, se seleccionaron dos grupos que representaron la totalidad de respuestas analizadas, denotados por G1 (integrado por E1 y E2) y G2 (integrado por E3 y E4). En ambos se reconoció una primera etapa de acción: separar los cuadrados ubicados dentro de la superficie de aquellos situados en su frontera, transformándose en un procedimiento de clasificación. Antes de realizarla, el grupo de estudiantes formuló lo medible, lo cual significó establecer que cada cuadrado tiene un área de 10.000 mts2. Al respecto, E1 señaló:

E1: Lo primero que hicimos fue saber cuántos cuadrados completos [refiriéndose a los cuadrados ubicados al interior de la superficie] teníamos en conjunto con mi compañero (…) y, en total, nos dieron 49 cuadrados completos.

Investigador: ¿Por qué trabajaron con los cuadrados completos?

E1: Porque su lado era de 100 metros, y lado por lado da 10.000 mts2, y para que pudiéramos aplicar esta fórmula [refiriéndose al área de un cuadrado] tenían que estar sí o sí completos.

Posteriormente, G1 continuó su razonamiento con aquellos cuadrados ubicados en la frontera de la superficie. Al respecto, E1 indicó:

E1: Luego, distribuimos, según nuestro criterio, los cuadrados faltantes que quedaban, yo conté cuántos había… 28.

Investigador: ¿28 qué?

E1: 28 incompletos [refiriéndose a los cuadrados ubicados en la frontera de la superficie], los cuales distribuí en porcentajes, por así decirlo, como por ejemplo que tengo 4 [refiriéndose a cuadrados ubicados en la frontera] que yo le asigné un 0,75 de un cuadrado completo.

En este diálogo, se reconoció que los estudiantes buscaron determinar qué porcentaje del área de un cuadrado completo le correspondía a cada uno de los cuadrados ubicados en la frontera. Lo anterior, se reforzó con lo señalado por E2:

E2: A algunas partes [refiriéndose a cuadrados ubicados en la frontera] le asigné 0,5 cuando se estimaba un valor aproximado que era la mitad de un cuadrado.

La Figura 8 muestra la asignación de porcentajes de G1 para los cuadrados ubicados en la frontera de la parte derecha de la superficie, junto con un conteo de cuadrados completos ubicados al interior.

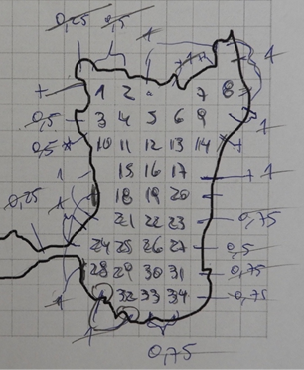
Figura 8. Asignación de porcentajes y conteo de cuadrados realizada por G1

Nota: fuente propia de la investigación.

Una vez terminada la asignación de porcentajes, G1 se enfocó en la parte izquierda de la superficie y sumó todos estos porcentajes para concluir que equivale a 16,55 cuadrados completos (Figura 9), a los cuales le sumaron los 15 cuadrados ubicados al interior, dando un total de 15 + 16,55 = 31,55 cuadrados completos. De manera similar, en la parte derecha de la superficie G1 determinó que los cuadrados ubicados en la frontera equivalen a 13,5 cuadrados completos, a los cuales le sumaron los 34 cuadrados ubicados al interior, dando un total de 34 + 13,5 = 47,5 cuadrados completos para la zona derecha.

Figura 9. Equivalencia de cuadrados incompletos a completos

Nota: fuente propia de la investigación.

Finalmente, G1 sumó los cuadrados completos de la parte izquierda y derecha para tener un total de 47,5 + 31,55 = 79,05 cuadrados completos. Esta cantidad de cuadrados permitió determinar el área de la superficie, la cual fue de 79,05·10.000 mts2 = 790.000 mts2, por lo que G1 infirió que la laguna se secará (Figura 10).

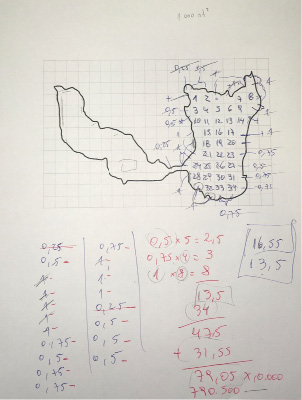
Figura 10. Desarrollo de G1 para determinar el área de la superficie

Nota: fuente propia de la investigación.

Respecto a los usos de la cuantificación de G1, su funcionamiento fue para determinar el área de la superficie plana, y su forma fue a través del producto 10.000 · n, donde n representa la cantidad de cuadrados completos cuya suma de áreas equivale, según los y las estudiantes, a la de la superficie en cuestión.

Por su parte, G2 también realizó un procedimiento de clasificación en cuadrados completos e incompletos, pero esta sirvió para acotar superiormente el área de la superficie. Al respecto, E3 señaló lo siguiente:

Investigador: ¿Qué hicieron?

E3: Contamos todos los cuadrados enteros [refiriéndose a los cuadrados completos] y, aparte, contamos los cuadrados incompletos, a los que les falta una fracción.

Investigador: ¿Cuántos cuadrados tienen?

E3: 45 [refiriéndose a los completos] y 46 incompletos.

Investigador: Los consideraron así.

E3: Y aunque fueran todos completos [refiriéndose a los cuadrados], igual tendríamos 91, y no alcanzan a tener 10 por lado para tener un kilómetro cuadrado.

La estrategia de G2 consistió en acotar superiormente el área de la superficie, es decir, esta área es menor al área de 91 cuadrados (maximizando cada cuadrado incompleto por uno completo), y esta área a su vez, es menor a 1 km2. Si bien G2 utilizó una estrategia de acotamiento, esta se inició por un procedimiento de clasificación que previamente requirió formular lo medible de cada cuadrado.

Respecto a los usos de la cuantificación de G2, su funcionamiento fue para acotar superiormente el área de la superficie, y su forma fue a través del producto 10.000 · n, donde n representa la cantidad mínima de cuadrados completos que cubren la superficie.

En términos de la ζ(Mod), en esta situación se evidenciaron dos usos de la cuantificación, uno realizado por G1 y otro por G2. Ambos ocurrieron en una situación de medición conformado por elementos que permitieron al grupo de estudiantes construir conocimiento matemático: significaciones asociadas a la medida de magnitudes (la superficie plana fue la magnitud y su área, en mts2, correspondió a su medida), procedimientos de clasificación de los cuadrados de la cuadrícula (completos e incompletos) y lo medible de estos cuadrados (área igual a 10.000 mts2) como instrumento, los cuales en conjunto derivaron en la argumentación de cuantificación de la medida de la superficie, siendo esta una resignificación de usos construida por el alumnado.

Formulación de una epistemología de usos de la cuantificación

Los usos de la cuantificación se resignifican en situaciones de medición de una comunidad interdisciplinar, de la obra matemática de Lebesgue (1902) y de estudiantes de ingeniería. Estos usos también se resignifican en las transversalidades entre estos escenarios. Los momentos de transversalidad son Mo1: cuantificación de bacterias coliformes, Mo2: construcción de la integral definida y Mo3: cálculo del área de una superficie plana. Cada momento señala una alternancia de dominios que genera debates entre funcionamientos y formas de los usos de la cuantificación en situaciones de medición conformadas por elementos que construyen conocimiento matemático: significaciones asociadas a la medida de magnitudes, procedimientos de clasificación e instrumentos ligados a lo medible, los que en conjunto derivan en argumentaciones de cuantificación. Esta epistemología de usos se muestra en la Tabla 3.

Tabla 3. Epistemología de usos de la cuantificación

Situación	Medición
Significaciones	Medida de magnitudes
Procedimientos	Clasificación
Instrumento	Lo medible
Argumentación/Resignificación	Cuantificación

Nota: fuente propia de la investigación.

Discusiones

Diversas investigaciones en educación matemática han estudiado la cuantificación desde distintas perspectivas teóricas. Por mencionar algunas de ellas, Silverman y Thompson (2008) realizaron un estudio con profesores para plantear la multiplicación como una operación de cuantificación. Moore (2013) estudió la cuantificación de la medida de ángulos que realizó un grupo de estudiantes desde la perspectiva cognitiva del razonamiento cuantitativo, en el sentido de Thompson (1990). Ahora bien, White (2019) analizó la cuantificación en el contexto de dos modelos en Física: movimiento con aceleración constante y el teorema del trabajo y la energía. Estas investigaciones justifican la importancia de la cuantificación para la matemática escolar y ofrecen referentes educativos para su enseñanza. Sin embargo, su foco de atención no está en los usos de la cuantificación que emergen del estudiantado ni en otros dominios de conocimiento, así como tampoco en la funcionalidad del conocimiento matemático. En ese sentido, esta investigación busca diferenciarse y aportar a la comunidad educativa al ofrecer un marco de referencia para la matemática escolar que valora dichos usos y la funcionalidad del conocimiento.

La epistemología de usos de la cuantificación sirve como base para el DSES que le permitan a la matemática escolar atender las justificaciones funcionales que demandan otros dominios de conocimiento y conformar elementos de diálogo entre la matemática escolar y el cotidiano de la gente. Estos diseños buscan que, a partir de una argumentación de cuantificación, el estudiantado formule lo medible para generar procedimientos de clasificación que le otorguen al conocimiento matemático significados asociados a la medida de magnitudes. La implementación de estos diseños contribuye a confrontar la enseñanza habitual de la cuantificación, en donde se cuantifican medidas de magnitudes geométricas por medio de diversos tipos de fórmulas. En concordancia con Marcía (2020), este tipo de diseños juegan un rol preponderante en la segunda línea de trabajo del programa SOLTSA, pues contribuyen a trastocar y transformar la matemática escolar a la espera de un impacto educativo.

Para la Socioepistemología, rescatar argumentaciones en diferentes escenarios provee elementos para la construcción de marcos de referencia que valoren la transversalidad y la pluralidad epistemológica. En esa dirección, y a partir de lo realizado en distintas investigaciones socioepistemológicas, se ha ido construyendo la Socioepistemología del Cálculo y el Análisis, marco de referencia que estructura, individual y conjuntamente, una epistemología de conocimiento matemático a partir de siete situaciones núcleo: variación, transformación y aproximación (Cordero, 2008), cambio (Marcía, 2020), selección (Cordero et al., 2019), ponderación (Medina, 2019) y periodización (Pérez-Oxté, 2021), las cuales están conformadas por significaciones, procedimientos, instrumentos y argumentaciones. En esa línea, la formulación de la epistemología de usos de la cuantificación amplía este marco, al incorporar la situación de medición (Figura 11). De esta forma, este marco se amplía, así como las situaciones escolares cuyo objetivo sea emprender aprendizajes de los significados de la matemática (Cordero et al., 2019).

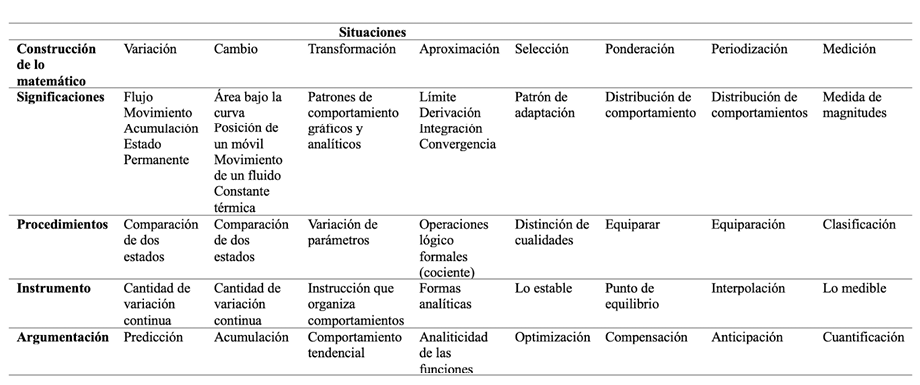
Figura 11. Socioepistemología del Cálculo y el Análisis

Nota: fuente propia de la investigación.

Conclusiones

La epistemología de usos formulada en esta investigación permite plasmar a la situación de medición como un referente educativo para establecer el uso, la resignificación y la transversalidad de la cuantificación.

Una como tarea para la comunidad educativa es generar programas permanentes de acompañamiento que permitan impactar en la formación de los y las estudiantes al implementar situaciones escolares diseñadas con base en la epistemología de usos de la cuantificación, las cuales le pueden permitir al estudiantado resignificar dichos usos en situaciones específicas de medición. Por ejemplo, se pueden diseñar situaciones que incluyan una gran cantidad de fichas de diferentes colores y pedirles a estudiantes cuantificar la cantidad total de fichas. Un procedimiento para realizar esto es clasificar las fichas en lotes del mismo color, para facilitar esta cuantificación. Además, estos lotes deben ser medibles (es decir, fáciles de contar). Esto permitirá cuantificar la cantidad total del conjunto de fichas, cuyo significado se asocia a la cardinalidad de dicho conjunto, la cual es una medida de conteo. En ese sentido, el aprendizaje de la cuantificación no estará relacionada con emular procedimientos matemáticos para determinar la medida de ángulos, perímetros, áreas y volúmenes, sino en desarrollar una autonomía de resignificaciones de usos de la cuantificación en diversas situaciones de medición y múltiples dominios de conocimiento.

Financiamiento

Proyecto Fondecyt de Iniciación N.° 11220346. Proyecto Fondecyt de Iniciación N.°11201103.

Conflicto de intereses

Las personas autoras declaran no tener algún conflicto de interés.

Declaración de la contribución de los autores

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo.

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: C. G. P. 25 %, F. C. O. 25 %, J. H. A. 25 % y J. M. L. 25 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente [C. G. P.], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://doi.org/10.5281/zenodo.10048909

Referencias

Acebo, J. y Rodríguez, R. (2019). Mathematical Modeling in the Educational Field: A Systematic Literature Review. Proceedings of the Seventh International Conference on Technological Ecosystems for Enhancing Multiculturality, 718-725. https://doi.org/10.1145/3362789.3362811

Borel, É. (1898). Leçons sur la Théorie des Fonctions. París: Gauthier-Villars.

Canela, L. (2016). Aritmetización del análisis y construcción formal: Husserl como alumno de Weierstrass y Kronecker. Eikasía: Revista de filosofía, 72, 135-152. https://dialnet.unirioja.es/servlet/articulo?codigo=6846667

Cantoral, R. (2013). Teoría Socioepistemológica de la Matemática Educativa. Estudios sobre construcción social del conocimiento. Barcelona: Gedisa.

Cauchy, A. (1823). Résumé des leçons données à l’École Royale Polytechnique sur le calcul infinitésimal. París: Imprimerie royale.

Cirillo, M., Pelesko, J., Felton-Koestler, M. y Rubel, L. (2016). Perspectives on Modeling in school Mathematics. En C. Hirsh, y A. R. McDuffie (Eds.), Annual Perspectives in Mathematics Education: Mathematical Modeling and Modeling Mathematics (pp. 3-16). National Council of Teachers of Mathematics.

Cordero, F. (2008). El uso de las gráficas en el discurso del cálculo escolar. Una visión socioepistemológica. En R. Cantoral, O. Covián, R. M. Farfán, J. Lezama y A. Romo (Eds.), Investigaciones sobre enseñanza y aprendizaje de las matemáticas: Un reporte Iberoamericano (pp. 285-309). México: Díaz de Santos.

Cordero, F. (2016). Modelación, funcionalidad y multidisciplinariedad: el eslabón de la matemática y el cotidiano. En J. Arrieta y L. Díaz (Eds.), Investigaciones latinoamericanas de modelación matemática educativa (pp. 59-88). Gedisa.

Cordero, F., Del Valle, T. y Morales, A. (2019). Usos de la optimización de ingenieros en formación: el rol de la ingeniería mecatrónica y de la obra de Lagrange. Relime, 22(2), 185-212. https://doi.org/10.12802/relime.19.2223

Cordero, F., Gómez, K., Silva-Crocci, H. y Soto, D. (2015). El discurso matemático escolar: la adherencia, la exclusión y la opacidad. Barcelona: Gedisa.

Cordero, F., Mendoza-Higuera, J., Pérez-Oxté, I., Huincahue, J. y Mena-Lorca, J. (2022). A Category of Modelling: The Uses of Mathematical Knowledge in Different Scenarios and the Learning of Mathematics. En M. Rosa, F. Cordero, D. Orey y P. Carranza (Eds.), Mathematical Modelling Programs in Latin America (pp. 247-4267). Springer, Cham. https://doi.org/10.1007/978-3-031-04271-3_12

Cordero, F. y Flores, F. (2007). El uso de la gráfica en el discurso matemático escolar. Un estudio socioepistemológico en el nivel básico a través de los libros de texto. Relime, 10(1), 7-38. https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-24362007000100002

Cordero, F. y Solís, M. (2022). Un cambio educativo: ¿Matemática para la Ingeniería? o ¿Matemática de la Ingeniería? En F. Cordero, M. Solís y C. Opazo (Eds.), La Matemática en la Ingeniería. Modelación y transversalidad de saberes (pp. 27-44). México: Gedisa.

Delgado, K. (2013). Estudio de la obtención de compósitos con propiedades antimicrobiales y antifouling formados por una matriz polimérica y nanopartículas a base de cobre. [Tesis de doctorado no publicada]. Universidad de Chile. https://repositorio.uchile.cl/handle/2250/115071

Díaz, E., Ortiz, N., Morales, K., Rebolledo, M., Barrera, R. y Norambuena, P. (2020). Texto del estudiante. Matemática 2° medio. Santiago: SM. https://www.curriculumnacional.cl/614/articles-145586_textoescolar_muestra.pdf

Dirichlet, G. (1829). Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, Journal für die reine und angewandte Mathematik, 4, 157-169. https://doi.org/10.1515/crll.1829.4.157

Flick, U. (2004). Introducción a la investigación cualitativa. Madrid: Morata.

Fresno, C., Torres, C. y Ávila, J. (2022). 1° medio. Matemática. texto del estudiante. Santiago: Santillana.

García, V. (2018). La clase de matemáticas como laboratorio socioepistemológico. Revista Latinoamericana De Etnomatemática Perspectivas Socioculturales De La Educación Matemática, 11(2), 142-165.

Holy, L. (1984). Theory, Methodology and Research Process. En Roy Ellen (Ed.), Ethnographic Research. A Guide of General Conduct (pp. 13-34). Academic Press.

Hygiena (s. f.). Microsnap. Rapid microorganism detection [Archivo PDF]. https://www.gemscientific.co.uk/downloads/1598621118Hygiena_MicroSnap_GS2019.pdf

Iturra, F., Manosalva, C., Ramírez, M. y Romero, D. (2022). Texto del estudiante. Matemática 7° Básico. Santiago: SM.

Jordan, C. (1892). Remarques sur les intégrales définies, Journal de mathématiques pures et appliquées, 4(8), 69-100. http://www.numdam.org/item/JMPA_1892_4_8__69_0/

Larina, G. (2016). Analysis of Real-World Math Problems: Theoretical Model and Classroom Application. VoprosyObrazovaniya/ Educational Studies, (3), 151-168, Moscú. https://doi.org/10.17323/1814-9545-2016-3-151-168

Lebesgue, H. (1902). Intégrale, Longueur, Aire. Annali di Matematica, 7, 231-359. https://doi.org/10.1007/BF02420592

Marcía, S. (2020). Resignificación de la integral en una comunidad de estudiantes de docencia de la matemática. una categoría de acumulación y la perspectiva de identidad disciplinar. [Tesis de maestría no publicada]. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México. https://repositorio.cinvestav.mx/handle/cinvestav/4030

Medina, D. (2019). Transformación educativa del docente de matemáticas. Un episodio: el uso de la compensación como una resignificación de la media aritmética. [Tesis de doctorado no publicada]. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México.

Mendoza, J. y Cordero, F. (2018). La modelación en las comunidades de conocimiento matemático. El uso de las matemáticas en ingenieros biónicos. El caso de la estabilidad. Revista Latinoamericana de Etnomatemática, 11(1), 36-61. https://www.redalyc.org/journal/2740/274058504003/html/

MINEDUC. (2015). Bases Curriculares 7º básico a 2º medio [Archivo PDF]. https://www.curriculumnacional.cl/614/articles-37136_bases.pdf

MINEDUC. (2018). Bases Curriculares Primero a Sexto básico [Archivo PDF]. https://www.curriculumnacional.cl/614/articles-22394_bases.pdf

Moore, K. (2013). Making sense by measuring arcs: a teaching experiment in angle measure, Educ Stud Math, 83, 225-245. https://doi.org/10.1007/s10649-012-9450-6

Morales, J. (2020). Resignificación de los usos de la derivada en un diseño escolar con perspectiva de dialéctica exclusión-inclusión: predicción, comportamiento tendencial y analiticidad. [Tesis de maestría no publicada]. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México. https://repositorio.cinvestav.mx/handle/cinvestav/3898

OCDE. (2017). Marco de Evaluación y de Análisis de PISA para el Desarrollo: Lectura, Matemáticas y Ciencias [Archivo PDF]. https://www.oecd.org/pisa/aboutpisa/ebook%20-%20PISA-D%20Framework_PRELIMINARY%20version_SPANISH.pdf

Osorio, G., Norambuena, P., Romante, M. Gaete, D., Díaz, J., Celedón, J., Morales, K., Ortiz, N., Ramírez, P., Barrera, R. y Hurtado, Y. (2019). Texto del estudiante. Matemática. 3° y 4° medio. Santiago: SM.

Paraje, M. y Tamagnini, L. (2015). ¿Qué son las bacterias viables no cultivables? (revisión literaria). Revista De La Facultad De Ciencias Exactas, Físicas y Naturales, 2(2), 99-102.

Parra, T. y Méndez, C. (2021). Ejemplos de metodologías de investigación que discuten sobre el papel de la diversidad en la matemática Educativa. En F. Cordero (Ed.), La Matemática Educativa y Latinoamérica (pp. 151-171). México: Gedisa.

Peek, L. y Guikema, S. (2021). Interdisciplinary Theory, Methods, and Approaches for Hazards and Disaster Research: An Introduction to the Special Issue. Risk Analysis, 41(7), 1047-1058. https://doi.org/10.1111/risa.13777

Pérez-Oxté, I. (2021). Anticipar-periodizar: una socialización de saberes matemáticos entre la Ingeniería y la docencia. [Tesis de doctorado no publicada]. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México.

Riemann, B. (1867). Uber die Darstellbarkeit einer Function durch eine trigonometrische Reihe. Göttingen: Dieterich.

Rojas, I. (2011). Elementos para el diseño de técnicas de investigación: Una propuesta de definiciones y procedimientos en la investigación científica. Tiempo de Educar, 12(24), 277-297. https://www.redalyc.org/articulo.oa?id=31121089006

Saxe, G. (2004). Practices of quantification from a sociocultural perspective. En K. A. Demetriou, y A. Raftopoulos (Eds.), Developmental change: Theories, models, and measurement (pp. 241-263). Nueva York: Cambridge University. https://doi.org/10.1017/CBO9780511489938.009

Stake, R. (1995). The Art of Case Study Research. Sage Publications.

Silverman, J. y Thompson, P. W. (2008). Toward a framework for the development of mathematical knowledge for teaching. Journal of Mathematics Teacher Education, 11, 499-511. https://doi.org/10.1007/s10857-008-9089-5

Thompson, P. W. (1990). A theoretical model of quantity-based reasoning in arithmetic and algebra. San Diego: Center for Research in Mathematics & Science Education, San Diego State University.

Torres, C. y Caroca, M. (2022). Texto del estudiante. Matemática 8° básico. Santiago: Santillana.

Villa-Ochoa, J. (2015). Modelación matemática a partir de problemas de enunciados verbales: un estudio de caso con profesores de matemáticas. Magis, 8(16), 133-148. https://dialnet.unirioja.es/servlet/articulo?codigo=5236344

White, S. (2019). Quantification and its importance to modeling in introductory physics, European Journal of Physics, 40(4), 1-13. https://doi.org/10.1088/1361-6404/ab1a5a

---

1. 1* Corresponding author

   Claudio Gaete-Peralta, claudio.gaete@ubo.cl, https://orcid.org/0000-0002-3747-3018

   Francisco Cordero, fcordero@cinvestav.mx, https://orcid.org/0000-0002-7891-7498

   Jaime Huincahue, jhuincahue@ucm.cl, https://orcid.org/0000-0003-0749-0551

   Jaime Mena, jaime.mena@pucv.cl, https://orcid.org/0000-0003-2274-4716

   Departamento de Matemáticas y Ciencias de la Ingeniería, Universidad Bernardo O´Higgins, Santiago, Chile.

1. 2 Centro de Investigación y de Estudios Avanzados, Instituto Politécnico Nacional, Ciudad de México, México.

1. 3 Centro de Investigación de Estudios Avanzados del Maule, Universidad Católica del Maule, Talca, Chile.

1. 4 Instituto de Matemáticas, Pontificia Universidad Católica de Valparaíso, Valparaíso, Chile.