Revista UNICIENCIA
Uniciencia Vol. 38(1), January-December, 2024
E-ISSN: 2215-3470
DOI: https://dx.doi.org/10.15359/ru.38-1.25
Caracterización de tareas sobre inecuaciones en libros de textos escolares en educación primaria
Characterization of inequation tasks in primary school textbooks
Caracterização de tarefas sobre inequações em livros didáticos do ensino fundamental
Estefanía Pacheco1*, Cristina Ayala-Altamirano2, Marta Molina3
Received: Sep/15/2023 • Accepted: Apr/3/2024 • Published: Aug/31/2024
|
Resumen [Objetivo] En este estudio se han caracterizado tareas matemáticas sobre inecuaciones en textos escolares chilenos de 4.o y 5.o curso (9 y 10 años) de educación primaria. [Metodología] Se realizó un estudio cualitativo de carácter descriptivo considerando seis categorías, a saber: las prácticas algebraicas involucradas, la estructura sintáctica de las expresiones, el significado del concepto de inecuación, estrategias de resolución, el nivel de demanda cognitiva y el contexto. La muestra está compuesta por 206 tareas extraídas de los libros de textos escolares de educación matemáticas. [Resultados] Las tareas caracterizadas evidencian escasas prácticas que conducen al pensamiento algebraico. Dentro de estas prácticas y, con mayor predominio, destaca la representación de tipo simbólica alfanumérica. La estructura de las expresiones da cuenta de escasa variedad para generalizar y razonar, esto último tiene repercusiones en las estrategias de resolución, las cuales no se tratan progresivamente, con el objetivo de mejorar su comprensión. Las tareas propuestas presentan diversos significados de la inecuación. En cuanto a demanda cognitiva la mayoría de las tareas consisten en procedimientos con y sin conexión. Por último, los contextos más frecuentes son los matemáticos y, con escasa presencia, los personales, sociales y ocupacionales. [Conclusiones] Se concluye necesario enriquecer el diseño de tareas. Las categorías propuestas son una herramienta para visualizar qué elementos se toman en consideración y permiten mejorar las tareas sobre inecuaciones. Palabras clave: Álgebra temprana; desigualdad matemática; educación primaria; inecuación; tarea matemática Abstract [Objective] This study characterized mathematical inequation tasks in Chilean primary school textbooks for 4th and 5th graders (9 and 10 year olds). [Methodology] A qualitative descriptive study was conducted considering the following six categories: algebraic practices involved, syntactic structure of the expressions, meaning of the concept of inequation, resolution strategies, level of cognitive demand, and context. The sample is comprised of 206 tasks from math textbooks. [Results] The characterised tasks have few practices leading to algebraic thinking, and it is the alphanumeric symbolic representation the one that predominantly stands out within these practices. The structure of the expressions shows little variety for generalising and reasoning, the latter having repercussions on the resolution strategies, which are not progressively addressed in order to improve their comprehension. The proposed tasks present different meanings of inequation. Regarding the cognitive demand, most of the tasks consist of connected and unconnected procedures. Finally, the most frequent contexts are mathematical, while the ones with the least presence are personal, social, and occupational contexts. [Conclusions] It is concluded that improving task design is necessary. The proposed categories are a tool to visualise which elements are taken into consideration and to improve inequation tasks. Keywords: Mathematical inequality; Early algebra; Inequations; Math task; Primary education Resumo [Objetivo] Neste estudo, foram caraterizadas tarefas matemáticas sobre inequações em livros escolares chilenos do 4º e 5º anos (9 e 10 anos de idade) do Ensino Fundamental. [Metodologia] Foi realizado um estudo qualitativo descritivo considerando seis categorias, a saber: as práticas algébricas envolvidas, a estrutura sintática das expressões, o significado do conceito de inequação, as estratégias de resolução, o nível de demanda cognitiva e o contexto. A amostra é composta por 206 tarefas extraídas de livros didáticos de educação matemática. [Resultados] As tarefas caracterizadas mostram poucas práticas que levam ao pensamento algébrico. Dentro dessas práticas, e com maior predominância, destaca-se a representação simbólica alfanumérica. A estrutura das expressões apresenta pouca variedade para generalizar e raciocinar, esta última repercute nas estratégias de resolução, que não são tratadas progressivamente, com o objetivo de melhorar sua compreensão. As tarefas propostas apresentam diferentes significados de inequação. Em termos de demanda cognitiva, a maioria das tarefas consiste em procedimentos com e sem conexão. Finalmente, os contextos mais frequentes são os matemáticos e, com pouca presença, os contextos pessoais, sociais e ocupacionais. [Conclusões] Conclui-se que é necessário enriquecer a concepção das tarefas. As categorias propostas são uma ferramenta para visualizar quais elementos são levados em consideração e permitem melhorar as tarefas sobre inequações. Palavras-chave: Álgebra inicial; desigualdade matemática; ensino fundamental; inequação; tarefa matemática |
Currículos de diversos países abordan el estudio de las desigualdades e inecuaciones en educación primaria. Por ejemplo, en las directrices curriculares de Chile y Estados Unidos este tema se contempla desde hace más de una década (National Governors Association Center for Best Practices and Council of Chief State School Officers, 2010 y Ministerio de Educación de Chile [MINEDUC], 2012). Mientras que, en Canadá, en la provincia de Ontario (Ontario Ministry of Education, 2020), y en España (Ministerio de Educación y Formación Profesional [MEFP], 2022) esta temática ha sido introducida recientemente.
Los currículos oficiales se suelen concretar en los textos escolares (Valverde et al., 2002), es por esto que, en este trabajo, nos interesamos por caracterizar las tareas sobre inecuaciones en dichos textos. Además, los ya mencionados son el recurso con mayor uso en las escuelas (Mullis et al., 2012; Sievert et al., 2021). Investigaciones previas han evidenciado al texto escolar como el principal apoyo de profesores y estudiantes (Christou et al., 2023).
Los elementos que nos permitirán caracterizar las tareas e identificar su carácter algebraico son las prácticas algebraicas (Blanton et al., 2018) y la estructura de las expresiones algebraicas (Vega-Castro, 2012). Por otro lado, identificaremos los significados de las inecuaciones (Paoletti et al., 2021), las estrategias de resolución (Ellis y Özgür, 2024; Kieran y Martínez-Hernández, 2022; Ngu et al., 2018; Pino-Fan et al., 2024; Radford, 2022), la demanda cognitiva (Smith y Stein, 1998) y los contextos PISA referidos en las tareas (OECD, 2022).
Las investigaciones enfocadas en el estudio de las desigualdades e inecuaciones en educación primaria son escasas. Warren (2006), en un estudio longitudinal con estudiantes de 8 a 10 años, observó una comprensión limitada del lenguaje relacionado con los conceptos de equivalencia y no equivalencia, en concreto, términos como: más, menos, igual y entre. Concluyó que estos conceptos escasamente se usan en las actividades curriculares de matemática. Por otro lado, la Agencia de Calidad de la Educación de Chile (2019) observó que estudiantes de edad similar (9 años), en pruebas estandarizadas nacionales e internacionales, presentan dificultades en las tareas sobre inecuaciones a causa de que las resuelven como si fueran ecuaciones.
Mayor cantidad de investigaciones sobre el tema se centran en estudiantes de educación secundaria o superior, producto de que este contenido, tradicionalmente, era tratado solo en estos niveles. Se observan dificultades en relación con las inecuaciones al transitar del enunciado verbal al simbolismo algebraico (p. ej., Garrote et al., 2004; Heredia y Palacios, 2014). Otras se atribuyen a la falta de conexión con los diferentes tipos de significados que se les reconocen a las inecuaciones (Ferretti et al., 2022; Paoletti et al., 2021). También se reportan dificultades en las desigualdades con valores en el conjunto de los números enteros, así como errores por descuido y conocimientos básicos deficientes para resolver inecuaciones algebraicas (Botty et al., 2015).
Por otra parte, uno de los citados estudios señala como línea abierta el estudio de las inecuaciones y su conexión con los textos escolares, la formación de profesores, la innovación curricular y la evaluación (Ferretti et al., 2022).
En vista de lo antes expuesto y motivadas por la carencia de trabajos centrados en desigualdades e inecuaciones en primaria, nos proponemos como objetivo caracterizar las tareas de inecuaciones incluidas en textos escolares chilenos de 4.° y 5.° (9 y 10 años) de primaria.
En este estudio el pensamiento algebraico, independientemente del enfoque del álgebra escolar que se considere, se relaciona con cuatro prácticas: (a) generalizar, (b) representar, (c) justificar y (d) razonar (Blanton et al., 2011). Al pensar algebraicamente se razona sobre la generalidad, se percibe una estructura algebraica a partir del estudio de relaciones en las operaciones y se analizan los cambios entre las cantidades involucradas (Kieran, 2004). Además, se hace referencia a cantidades desconocidas y se trata dichas cantidades de forma analítica (Radford, 2018).
La generalización se considera esencial en el pensamiento algebraico (Kaput, 2008). Mason (2017) señala que generalizar es reconocer aquellos atributos que cambian, en tanto que otros permanecen invariables.
Las representaciones permiten hacer presentes los objetos matemáticos (Rico, 2009) y la consideración de diversas representaciones de un objeto matemático permiten una comprensión profunda de dicho objeto (Carraher et al., 2008). En concreto la inecuación puede ser representada de diversas formas: verbal (oral o escrito), pictórica (atributos visuales, en los que los objetos son representados por medio de dibujos o imágenes), simbólica alfanumérica (números, símbolos para las cantidades desconocidas y operaciones aritméticas), y múltiple, donde involucra dos o más tipos de representaciones.
La justificación en el aula de matemática es aquella práctica que promueve explicar conjeturas o afirmaciones. Brinda una oportunidad al estudiantado de detallar y manifestar sus ideas (Stephens et al., 2017) y constituye una herramienta para acceder a varias formas de razonamiento matemático (Thanheiser y Sugimoto, 2022).
La práctica de razonar implica utilizar las generalizaciones como objetos en sí mismos (Blanton et al., 2018). En particular, esta práctica conduce a los estudiantes a emplear las generalizaciones en situaciones matemáticas nuevas y diversas.
Una estructura algebraica tiene asociados significados, dependiendo del enfoque del álgebra escolar que se considere (Molina y Cañadas, 2018). En nuestro estudio, la estructura de una expresión algebraica tiene que ver con los términos que la componen, con los signos que la relacionan, con las diferentes operaciones y las relaciones que existen entre sus elementos (Castro et al., 1997). En el estudio de las expresiones algebraicas se puede hacer la distinción entre estructura externa, superficial o sintáctica y estructura interna u oculta de una expresión algebraica (Kirshner, 1989) según, si refiere a la apariencia de la expresión o al valor de esta. Por ejemplo, (x + 8)2 y (2x + 6)2 tienen la misma estructura externa al ser ambos cuadrados de binomios de primer grado, pero distinta estructura interna, al no ser equivalentes.
Hallazgos en el contexto de la ecuación, que pueden ser transferidos al contexto de las inecuaciones, refieren al análisis de la estructura realizando un estudio sintáctico a partir de diversos elementos: operatorias, ubicación del dato desconocido, representación del dato desconocido (Fernández-Millán y Molina, 2016; Vega-Castro, 2012). Fernández-Millán y Molina (2016) concluyen que el estudiantado de secundaria tiene mayor facilidad al trabajar con estructuras aditivas. Además, ante la demanda de formular problemas, a partir de expresiones simbólicas, observan la tendencia de proponer problemas donde la traducción simbólica ya tiene la incógnita despejada, lo que las autoras asocian a una visión operacional, centrada en el cálculo. Por lo tanto, sugieren dirigir la atención a los aspectos estructurales durante la enseñanza del álgebra. Por otra parte, Vega-Castro (2012) coincide en señalar la necesidad de dirigir la atención a la estructura, a partir de un estudio sobre los procesos de simplificación de expresiones algebraicas, para el alumnado de educación secundaria, que tiene como foco el constructo sentido estructural, este último, entendido como la capacidad de: percibir, comparar y relacionar las estructuras de diversas expresiones y seleccionar procedimientos adecuados para utilizar en las mismas.
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas, que involucran una cantidad desconocida o incógnita (Lloyd et al., 2011). Resolver una inecuación consiste en determinar todos los posibles valores de la incógnita que satisfacen la inecuación (Martínez et al., 2013). Sobre las estrategias para resolver inecuaciones en primaria, existe escasa literatura; por tanto, nos apoyamos en las investigaciones sobre ecuaciones. Nos centramos en cinco estrategias: estructural (Kieran y Martínez-Hernández, 2022), analítica (Radford, 2022), metáfora de balanza (Pino-Fan et al., 2024), ensayo y error (Ellis y Özgür, 2024) y, método inverso (Ngu et al., 2018).
Las dos primeras centran su atención en la estructura de la expresión algebraica y comparten la idea de que, en el caso de las ecuaciones, requieren de un significado relacional del signo igual, en el caso de las inecuaciones este significado se debe transferir a los signos de desigualdad.
La estrategia estructural se basa en realizar cambios en la estructura de la expresión por medio de la descomposición de expresiones y el uso de propiedades aritméticas para establecer relaciones entre los términos de la expresión.
La estrategia analítica se asienta en la transformación de la expresión algebraica con base en propiedades de la igualdad o desigualdad: sumar, restar, multiplicar o dividir, de igual modo uno y otro lado de la igualdad o desigualdad, sin que se vea alterada la relación de ambos miembros.
La metáfora de balanza es una estrategia que se apoya en el uso de balanzas, las cuales son representadas de manera concreta, pictórica, simbólica o virtual. A través del uso de estas se visualizan las transformaciones en las expresiones, las que suelen basarse en las propiedades de las igualdades o desigualdades, tal como la estrategia analítica antes mencionada.
La estrategia de ensayo y error consiste en asignar un valor a la incógnita y probar si dicho valor hace verdadera la relación. Esta estrategia es más intuitiva y algunas investigaciones previas han señalado que puede limitar el uso de otras estrategias (Ellis y Özgür, 2024).
Por último, el método inverso consiste en operar en uno de los miembros de la inecuación aplicando las relaciones existentes entre las operaciones aritméticas, de ser una inversa de otra (suma y resta, multiplicación y división).
Como se menciona previamente, una característica esencial de las inecuaciones es que la incógnita puede tener asociado uno o más valores. Razonar sobre esto implicará que surjan distintos significados asociados a las inecuaciones: ordenar y acotar (Borello, 2010), o comparativo y restrictivo (Paoletti et al., 2021). Aunque los significados tienen denominaciones distintas, sus descripciones son similares. En primer lugar, Borello (2010) denomina ordenar (comparar) a lo que Paoletti et al., (2021) denominan comparativo. Este significado se evidencia cuando se razona sobre magnitudes relativas a los valores numéricos de dos o más cantidades. Por ejemplo, en la expresión 4x<12, se comparan dos expresiones o cantidades distintas 4x y 12, la desigualdad indica cómo se relacionan, 4x debe ser menor que 12, y su solución se corresponde a un valor en el que haga verdadera la relación de desigualdad. En segundo lugar, el significado acotar (Borello, 2010) o restrictivo (Paoletti et al., (2021)) conlleva razonar sobre un intervalo de soluciones. Siguiendo con el mismo ejemplo, al resolver 4x<12 se presenta una restricción de los valores de x, en este caso, es equivalente a expresar x<3. Los significados estarán sujetos a lo que sugiere la tarea asignada.
Las investigaciones antes mencionadas coinciden en la importancia de fomentar distintos significados en las tareas sobre inecuaciones. Paoletti et al., (2021) concluyen que atender a los distintos significados de desigualdades, de manera explícita, en su distinción comparativa y restrictiva, contribuye a desarrollar significados más sofisticados para la desigualdad.
La inecuación en el currículo de educación primaria
Los libros de texto de matemáticas desempeñan un rol fundamental al momento de traducir la política educativa (Valverde et al., 2002). Es, por esta razón, que previo a realizar el análisis de los textos escolares, describimos el contexto curricular de Chile.
El currículo de Chile promueve el desarrollo del pensamiento algebraico a través del eje temático denominado patrones y álgebra. En los programas de estudio se pretende que el estudiantado explique y describa múltiples relaciones, a la vez que, las representen de diversos modos (concretas, pictóricas y simbólicas) (MINEDUC, 2012). De forma transversal a todos los ejes temáticos se promueve el desarrollo de las habilidades de argumentar y comunicar, resolver problemas, modelar y representar. Es a través de estas que se podrían desarrollar las cuatro prácticas algebraicas mencionadas en apartados previos.
La enseñanza de la desigualdad inicia en 1.º y 2.º curso de primaria, con el estudio de desigualdades numéricas, las cuales se asocian a situaciones de desequilibrio, utilizando la balanza como principal representación. Las relaciones de desigualdad en 1.° se expresan con palabras “mayor que” y “menor que”, mientras que desde 2.° se promueve el uso de símbolos > y <.
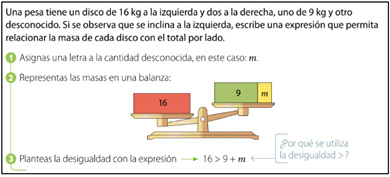
La inecuación se estudia en 4.° y 5.° curso. En ambos, los objetivos explicitan el estudio de inecuaciones de un paso, que involucran sumas y restas, tal como se muestra en la Figura 1.

Figura 1. OA de 4.° y 5.° de primaria
En las tareas sugeridas a los docentes, el programa de estudio propone incluir las relaciones “mayor que” y “menor que” representadas de forma pictórica y simbólica. Se continúa con el uso de la balanza como medio para representar una inecuación. En 4.° la representación de la incógnita es a través de figuras geométricas, mientras que en 5.° no especifica el tipo de representación, aunque en el tratamiento de las ecuaciones se sugiere el uso de letras, por lo que se podría transferir su uso a las inecuaciones.
El currículo de Chile, en lo que respecta al tratamiento de las desigualdades, es similar a otros currículos, tal como Ontario y España, lo que señala la importancia en el nivel internacional de esta temática. Se observa coincidencia en la introducción en 4.º y 5.° curso de desigualdades con cantidades desconocidas, representadas por medio de letras o figuras.
Nivel de demanda cognitiva y contextos
Las tareas presentes en los libros de textos inciden en el aprendizaje del estudiantado (Penalva y Llinares, 2011), por tanto, es importante evaluar las oportunidades de aprendizaje que estas ofrecen. Considerando lo anterior, empleamos dos criterios para la caracterización de las tareas: la demanda cognitiva y el contexto al que refieren.
Smith y Stein (1998) distinguen cuatro niveles de demanda cognitiva, de acuerdo con lo que la tarea requiere, que el alumnado realice: (a) memorización (M), entendida como la reproducción de hechos, reglas o fórmulas ya aprendidos, además, lo que debe reproducirse está claramente indicado y no son ambiguas; (b) procedimiento sin conexión (PSC), requiere el uso de un procedimiento sin conectar con los conceptos subyacentes ni requerir explicación o se centra en describir el procedimiento; (c) procedimiento con conexión (PCC), señala representar de diversas maneras los conceptos implicados y conectar los modos de representación, centran la atención en el uso de procedimientos para desarrollar mayores niveles de comprensión de ideas y conceptos matemáticos; y (d) hacer matemáticas (HM), demanda un pensamiento complejo y no algorítmico, la exploración de conceptos, procesos y relaciones, así como el análisis de la tarea en busca de restricciones que determinen posibles soluciones y estrategias. Requieren un considerable esfuerzo cognitivo.
Por otra parte, los contextos en los que están inmersas las tareas colaboran a situar los conceptos, desde su aplicación y trabajo. Actualmente la evaluación matemática PISA (OECD, 2022) sugiere diversidad de contextos, tales son: a) personal, refiere a actividades cotidianas del individuo (ya sea grupo familiar o compañeros); b) ocupacional, relaciona situaciones centradas en el mundo del trabajo, considerando desde trabajos no especializados hasta trabajos con nivel cualificado; c) social, refiere al contexto social, comunidad local, nacional o internacional, en la que se observan determinados aspectos del entorno y la perspectiva de la comunidad; d) científico, describe la aplicación de las matemáticas al mundo real y responde a asuntos vinculados con la ciencia y la tecnología.
En esta investigación seguimos un enfoque cualitativo de carácter descriptivo (Hernández-Sampieri y Mendoza, 2018). Nuestro objetivo es caracterizar tareas sobre inecuaciones en textos escolares chilenos de 4.° y 5.° curso (9 y 10 años) de primaria, atendiendo a las siguientes características: prácticas algebraicas (Blanton et al., 2018), análisis sintáctico de las expresiones involucradas (Vega-Castro, 2012), significado del concepto de inecuación (Paoletti et al., 2021), estrategias de resolución (Ellis y Özgür, 2024; Kieran y Martínez-Hernández, 2022; Ngu et al., 2018; Pino-Fan et al., 2024; Radford, 2022) nivel de demanda cognitiva (Smith y Stein, 1998) y contexto al que refiere PISA (OECD, 2022).
Analizamos textos escolares chilenos distribuidos de modo gratuito por el MINEDUC en colegios públicos y concertados; por tanto, son de amplio uso en las comunidades educativas. Se analizaron dos proyectos distintos (Sumo Primero [SP] y Santillana [SA]), compuestos por: un texto para el estudiante, un cuaderno de ejercitación, un set de ticket de salida (para el proyecto SP) y un texto guía para el docente (Anexo 1). Nombramos los proyectos como: SP-4, SP-5, SA-4 y SA-5, donde los números 4 y 5 corresponden al nivel educativo (4.° y 5.° curso).
El proyecto SA-5 se emplea desde el año 2017, mientras que el resto de los textos se emplean desde el año 2020. Todos los proyectos siguen vigentes para el curso académico 2024. Se identificaron un total de 206 tareas sobre inecuaciones.
En primer lugar, seleccionamos las tareas sobre inecuaciones y luego las clasificamos en tres grupos: tareas de plantear inecuación (Figura 2), tareas de resolver inecuación (Figura 3) y tareas mixtas (Figura 4). Estas categorías surgen del análisis de los textos escolares y los objetivos de las tareas.
|
|
|
|
|
Basándonos en la literatura previa planteamos a priori las categorías que se exponen en la Tabla 1. Posterior al análisis de las tareas los elementos que componen algunas subcategorías fueron complementados. En el análisis sintáctico se incluyó: selección de la operatoria, selección de ubicación, letra x, letra distinta a x, múltiples relaciones de desigualdad, selección de relación de desigualdad.
Tabla 1. Categorías de análisis
|
Categoría |
Subcategoría |
Elementos |
|
1. Prácticas algebraicas |
1.1. Generalizar 1.2. Razonar 1.3. Justificar |
|
|
1.4. Representar |
1.4.1. Verbal 1.4.2. Pictórica 1.4.3. Simbólica alfanumérica 1.4.4. Múltiple |
|
|
2. Análisis sintáctico de las expresiones |
2.1. Operatorias |
2.1.1. Suma 2.1.2. Resta 2.1.3. Selección de operatoria (la tarea requiere elegir la operación a emplear para desarrollar la tarea) 2.1.4. No presenta operatoria |
|
2.2. Ubicación del dato desconocido |
2.2.1. Derecha 2.2.2. Izquierda 2.2.3. Selección de ubicación (la tarea requiere decidir qué ubicación tendrá el dato desconocido) |
|
|
2.3. Representación del dato desconocido |
2.3.1. Letra x 2.3.2. Letra distinta a x 2.3.3. Figuras (geométricas o imágenes) 2.3.4. Lenguaje verbal |
|
|
2.4. Relación de desigualdad |
2.4.1. Mayor que (>) 2.4.2. Menor que (<) 2.4.3. Mayor o igual que (≥) 2.4.4. Menor o igual que (≤) 2.4.5. Múltiples relaciones de desigualdad 2.4.6. Selección de relación de desigualdad (la tarea requiere decidir la relación de desigualdad a emplear) |
|
|
3. Significado del concepto inecuación |
3.1. Comparativo 3.2. Restrictivo |
|
|
4. Estrategias de resolución (Ellis y Özgür, 2024; Kieran y Martínez-Hernández, 2022; Ngu et al., 2018; Pino-Fan et al., 2024; Radford, 2022) |
4.1. Estructural 4.2. Analítica 4.3. Metáfora de balanza 4.4. Ensayo y error 4.5. Método inverso |
|
|
5. Nivel de demanda cognitiva |
5.1. Memorización 5.2. Proceso sin conexión 5.3. Proceso con conexión 5.4. Hacer matemáticas |
|
|
6. Contextos PISA usados en las tareas (OECD, 2022) |
6.1. Personal 6.2. Ocupacional 6.3. Social 6.4. Científico |
|
Nota: Fuente propia de la investigación.
En nuestro proceso de investigación utilizamos la triangulación para asegurar la validez interna. La codificación de los datos se realizó de modo sistemático, para garantizar la fiabilidad. Realizamos revisiones periódicas, en las cuales la primera autora se encarga de la codificación inicial. En caso de discrepancias, establecemos diálogos para llegar a una decisión final.
En la Tabla 2 se muestra la clasificación de las tareas según su objetivo: plantear inecuación, resolver inecuación y tareas mixtas. Se puede apreciar que las tareas predominantes, en todos los cursos, son de resolución. Destacamos como de 4.° a 5.° curso aumentan dichas tareas en ambos proyectos. Las tareas de plantear inecuación, si bien están presentes en ambos cursos, se observan, en mayor cantidad, en 4.°, para ambos proyectos.
Tabla 2. Cantidad de tareas según el tipo
|
Tipo de tarea |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Plantear inecuación |
12 |
6 |
12 |
7 |
|
Resolver inecuación |
27 |
50 |
27 |
37 |
|
Mixtas |
3 |
8 |
10 |
7 |
|
Total |
42 |
64 |
49 |
51 |
Nota: Fuente propia de la investigación.
En los siguientes apartados caracterizamos, en detalle, cada uno de estos grupos considerando las categorías de la Tabla 1.
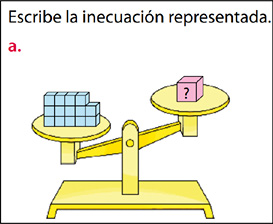
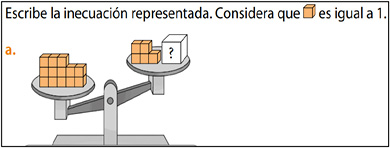
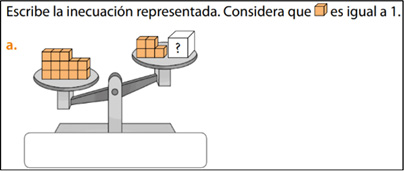
Estas tareas se centran en la traducción entre distintos tipos de representación. La instrucción en estos casos es: escribe la inecuación, escribe la expresión matemática que represente el problema, ¿cómo se podría representar esta situación en una balanza?
En los dos proyectos predominan las representaciones de tipo simbólica alfanumérica, siendo el proyecto SA el que presenta una mayor diversidad de representaciones (Tabla 3). Agregamos que, con respecto a las prácticas algebraicas, solo se detecta la de representar.
Tabla 3. Cantidad de tareas que evidencian representaciones
Nota: Fuente propia de la investigación.
Para el análisis sintáctico de las tareas hemos considerado la expresión simbólica contenida en el enunciado de esta y, en aquellos casos donde no venía sugerida la expresión hemos traducido la representación presente en la tarea, en una expresión simbólica procediendo de izquierda a derecha, para su posterior análisis. Presentamos, en la Tabla 4, la categoría de analisis sintáctico y los elementos que componen las expresiones.
Tabla 4. Análisis sintáctico en expresiones
|
Subcategoría |
Elementos |
SP-4 (n=12) |
SP-5 (n=6) |
SA-4 (n=12) |
SA-5 (n=7) |
|
Operatoria |
Suma |
8 |
2 |
7 |
5 |
|
Resta |
0 |
0 |
3 |
0 |
|
|
Selección de operatoria |
0 |
0 |
0 |
0 |
|
|
No presenta operatoria |
4 |
4 |
2 |
2 |
|
|
Ubicación del dato desconocido |
Derecha |
5 |
0 |
7 |
2 |
|
Izquierda |
5 |
2 |
4 |
5 |
|
|
Selección de ubicación |
2 |
4 |
1 |
0 |
|
|
Representación del dato desconocido |
Letra x |
0 |
4 |
3 |
4 |
|
Letra distinta a x |
0 |
0 |
0 |
3 |
|
|
Figuras |
10 |
0 |
8 |
0 |
|
|
Lenguaje verbal |
2 |
2 |
1 |
0 |
|
|
Relación de desigualdad |
Mayor que (>) |
3 |
0 |
6 |
4 |
|
Menor que (<) |
7 |
2 |
5 |
3 |
|
|
Mayor o igual que (≥) |
0 |
0 |
0 |
0 |
|
|
Menor o igual que (≤) |
0 |
0 |
0 |
0 |
|
|
Múltiples relaciones de desigualdad |
0 |
0 |
0 |
0 |
|
|
Selección de relación de desigualdad |
2 |
4 |
1 |
0 |
Nota: Fuente propia de la investigación.
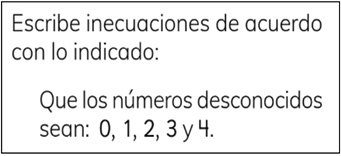
Se observa la presencia de tareas que no presentan operatoria, predominando las de estructura aditiva. En lo que concierne a la ubicación del dato desconocido en este tipo de tareas se representa, tanto a la izquierda como a la derecha de la desigualdad. Un ejemplo de tarea donde deben seleccionar la ubicación del dato desconocido se puede ver en la Figura 10. En la representación del dato desconocido, se observa que predomina el uso de la letra x en quinto, mientras que en cuarto se emplea, mayormente, las figuras, como cubos y cuadrados. SA-5 emplea otras letras como: m, y, z. Destacamos que, en tareas con empleo de lenguaje verbal, la cantidad desconocida o incógnita se halla en el contexto, siendo presentada, de modo explícito, a través de la palabra clave “desconocidos”, por ejemplo, la Figura 8.
La relación de desigualdad es expresada mayormente empleando el signo <, aunque la diferencia con las tareas que emplean el signo >, no es significativa.
Respecto a la demanda cognitiva, observamos tareas solo de alta demanda: de HM en todos los textos y PCC, con excepción en SP-5 (Tabla 5).
Tabla 5. Cantidad de tareas según el nivel de demanda cognitiva
|
Demanda cognitiva |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Procedimiento con conexión (PCC) |
10 |
0 |
9 |
5 |
|
Hacer matemáticas (HM) |
2 |
6 |
3 |
2 |
|
Total |
12 |
6 |
12 |
7 |
Nota: Fuente propia de la investigación.
Las Figuras 9 y 10, ambas son de traducción, en la primera de PCC, solo se centra en otro tipo de representación, o también traducir una expresión, cada dato viene otorgado en la balanza. Luego, la tarea de HM para realizar dicha traducción debe comprender conceptos y relaciones, atender a la restricción presentada y coincidir con la selección del posible empleo de operatoria, selección de ubicación y representación del dato desconocido, así también de la selección de relación de desigualdad.
|
|
|
|
Figura 9. Ejemplo de tarea con demanda cognitiva PCC, SA-4, p. 94 |
Figura 10. Ejemplo de tarea con demanda cognitiva HM, SP-4, p. 42 |
La Tabla 6 muestra la cantidad de cada tipo de contextos empleados. En todos los textos predomina el contexto científico, considerando el hecho de tratar con elementos de la matemática en que son presentadas las tareas (por ejemplo, las Figuras 9 y 10). Los contextos personal y social solo se observan en SA-4.
Tabla 6. Cantidad de tareas con contextos empleados
|
Contextos |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Personal |
0 |
0 |
1 |
0 |
|
Ocupacional |
0 |
0 |
0 |
0 |
|
Social |
0 |
0 |
1 |
0 |
|
Científico |
12 |
6 |
10 |
7 |
|
Total |
12 |
6 |
12 |
7 |
Nota: Fuente propia de la investigación.
Las tareas de resolver inecuación se centran en hallar el o los valores que satisfacen la desigualdad. En estas tareas solo se observa la práctica de justificar en 5.° curso, en ambos proyectos. Se evidencia en SP-5 en 3 tareas y en SA-5 en 14 tareas. Las instrucciones en estas tareas son explicar o justificar. La Figura 11 presenta un ejemplo.

Figura 11. Ejemplo tarea con práctica justificar, SA-5, p. 48
En cuanto al análisis sintáctico, atendemos a los mismos elementos que en las tareas de plantear inecuaciones (Tabla 7). Observamos que sigue predominando la suma en la estructura de las expresiones, pero, a diferencia de las tareas de plantear inecuaciones, en las tareas de resolver inecuaciones se incluyen expresiones con restas.
Tabla 7. Análisis sintáctico en expresiones
|
Subcategoría |
Elementos |
SP-4 (n=27) |
SP-5 (n=50) |
SA-4 (n=27) |
SA-5 (n=37) |
|
Operatoria |
Suma |
27 |
47 |
13 |
27 |
|
Resta |
0 |
3 |
9 |
9 |
|
|
Selección de operatoria |
0 |
0 |
0 |
0 |
|
|
No presenta operatoria |
0 |
0 |
5 |
1 |
|
|
Ubicación del dato desconocido |
Derecha |
0 |
0 |
4 |
11 |
|
Izquierda |
27 |
50 |
19 |
26 |
|
|
Selección de ubicación |
0 |
0 |
4 |
0 |
|
|
Representación del dato desconocido |
Letra x |
0 |
50 |
22 |
19 |
|
Letra distinta a x |
0 |
0 |
0 |
18 |
|
|
Figuras |
27 |
0 |
0 |
0 |
|
|
Lenguaje verbal |
0 |
0 |
5 |
0 |
|
|
Relación de desigualdad |
Mayor que (>) |
14 |
8 |
11 |
17 |
|
Menor que (<) |
13 |
23 |
12 |
20 |
|
|
Mayor o igual que (≥) |
0 |
7 |
0 |
0 |
|
|
Menor o igual que (≤) |
0 |
7 |
0 |
0 |
|
|
Múltiples relaciones de desigualdad |
0 |
5 |
0 |
0 |
|
|
Selección de relación de desigualdad |
0 |
0 |
4 |
0 |
Nota: Fuente propia de la investigación.
Con respecto a la ubicación del dato desconocido, se observa en la Tabla 7 que, a diferencia de las tareas de plantear inecuaciones, en las tareas de resolver inecuaciones, en la mayoría de las expresiones, este dato se ubica en la izquierda de la desigualdad, incluso en SP nunca está a la derecha. Por otra parte, continúa la tendencia de emplear la letra x para representar el dato desconocido, aunque en SP-4 se emplean figuras y en SA-5 se introducen otras letras (a, m, n, p, q, s, w, y, z).
Las relaciones de mayor que y menor que siguen predominando en las tareas, aunque el texto SP-5 introduce las relacionas mayor o igual que y menor o igual que. Esta relación se presenta en contraste con las otras, en tareas como la que se muestra en la Figura 12.

Figura 12. Ejemplo de tarea con múltiples relaciones de desigualdad, SP-5, p. 73
En tareas con problemas de palabras, identificamos palabras claves que nos permiten observar las relaciones de desigualdad, algunas de las palabras son: inclinada al lado, aumentar, sin igualar, más que, mayor que, menos que, mayor o igual que, menor o igual que, por mencionar algunas; otro modo es desde la observación (visual) de lo que ocurre con la balanza. Palabras como, máximo y mínimo son utilizadas para seleccionar la respuesta en el conjunto de soluciones y no para la relación de desigualdad.
Los significados son evidenciados, por primera vez, en este tipo de tareas, dado que están asociados a la solución de la inecuación (Tabla 8). En el proyecto SP, de 4.° a 5.° aumenta la cantidad de tareas para ambos significados. Situación contraria ocurre en SA en el significado restrictivo, las cuales disminuyen en cantidad de 4.° a 5.°. En general, se observan más tareas en las que no se promueve un significado explícitamente, por eso no se evidencia en las instrucciones (Figura 15). Los textos dejan abierta la posibilidad a que el alumnado plantee todas las soluciones que satisfacen la relación o algún ejemplo.
Tabla 8. Clasificación de tareas según su significado
|
Significado |
Ejemplo |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Comparativo |
5 |
15 |
2 |
3 |
|
|
Restrictivo |
|
0 |
20 |
25 |
3 |
|
No evidencia |
|
22 |
15 |
0 |
31 |
|
Total |
27 |
50 |
27 |
37 |
Nota: Fuente propia de la investigación.
Ambos proyectos presentan, al inicio de cada tema, una situación contextualizada en la que muestran distintas estrategias de resolución de inecuaciones. En SA-4 se introduce la balanza y el ensayo y error (Figura 16). En SA-5 se ejemplifican las estrategias de la balanza y la analítica (Figura 17). Por su parte, en SP se utiliza, además, el método inverso (Figura 18).
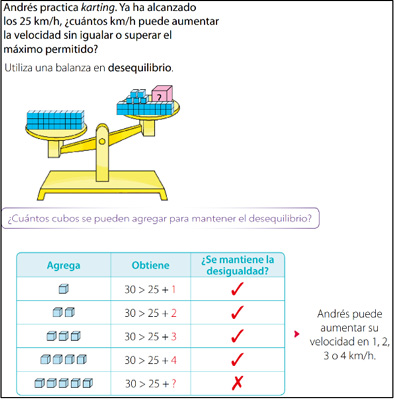
Figura 16. Ejemplo de estrategia balanza y ensayo y error, SA-4, p. 115
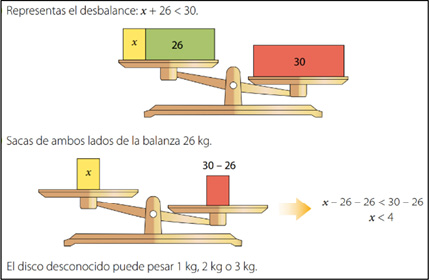
Figura 17. Ejemplo de estrategia balanza y analítica, SA-5, p. 62

Figura 18. Ejemplo de estrategia método inverso, SP-5, p. 46
En la Tabla 9 presentamos un resumen de las estrategias que se solicita emplear explícitamente en las tareas. Más de la mitad de las tareas no sugieren uso de las estrategias. Observamos que el texto SP-5 explicita mayor diversidad de estrategias.
Tabla 9. Cantidad de tareas que solicitan empleo de estrategias
|
Estrategias |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Estructural |
0 |
0 |
0 |
0 |
|
Analítica |
0 |
0 |
0 |
2 |
|
Metáfora de balanza |
4 |
2 |
8 |
0 |
|
Ensayo y error |
0 |
2 |
1 |
0 |
|
Método inverso |
0 |
3 |
0 |
0 |
|
No evidencia |
23 |
43 |
18 |
35 |
|
Total |
27 |
50 |
27 |
37 |
Nota: Fuente propia de la investigación.
Según la demanda cognitiva solo se identifican tareas de los tipos PCC y PSC (Tabla 10), salvo SA-4.
Tabla 10. Cantidad de tareas según el nivel de demanda cognitiva
|
Demanda cognitiva |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Procedimiento sin conexión (PSC) |
26 |
46 |
0 |
18 |
|
Procedimiento con conexión (PCC) |
1 |
4 |
27 |
19 |
|
Total |
27 |
50 |
27 |
37 |
Nota: Fuente propia de la investigación.
La tarea en la Figura 19 solicita el o los valores desconocidos; por lo tanto, podría desarrollar un cálculo algorítmico, apoyado en el conteo o con la estrategia de ensayo y error, por mencionar algunos. Por otro lado, en la Figura 20 la tarea fomenta el cálculo, a través de la visibilidad de los procedimientos empleados, mediante la estrategia utilizada para llegar a las soluciones.

Figura 19. Ejemplo de tarea con demanda cognitiva PSC, SP-4, p. 55
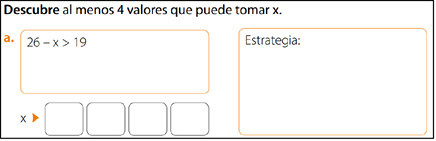
Figura 20. Ejemplo de tarea con demanda cognitiva PCC, SP-4, p. 94
En las tareas se utilizan contextos de tipo personal, ocupacional, social y científico (Tabla 11). Al igual que las tareas de plantear inecuación, el contexto científico tiene una mayor presencia en todos los proyectos. El contexto personal está asociado a tareas que aluden a situaciones sobre la vida cotidiana del alumnado, tal como se ejemplifica en la Figura 14. Los contextos social y ocupacional hacen referencia a empaquetar, agrupar y ordenar productos.
Tabla 11. Cantidad de tareas con contextos empleados
|
Contextos |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Personal |
1 |
0 |
4 |
0 |
|
Ocupacional |
0 |
2 |
0 |
0 |
|
Social |
0 |
0 |
1 |
0 |
|
Científico |
26 |
48 |
22 |
37 |
|
Total |
27 |
50 |
27 |
37 |
Nota: Fuente propia de la investigación.
Las tareas mixtas requieren plantear y resolver inecuaciones. Respecto a las prácticas algebraicas solo se identifica la representación (Tabla 12). Se formulan a través de instrucciones que, solicitan resolver o calcular y, luego, representar o viceversa, lo que es propio del tipo de tareas mixtas.
Tabla 12. Cantidad de tareas que evidencian representaciones
Nota: Fuente propia de la investigación.
En el análisis sintáctico de las expresiones (Tabla 13) se observa que continúa la tendencia a proponer expresiones relacionadas con sumas, en solo un caso se propone una resta. Dado que estas tareas requieren que el alumnado represente la inecuación, hay un mayor número de tareas en las que deben seleccionar dónde ubicar el dato desconocido y cómo presentarlo, además, de cuál es la relación de desigualdad que emplearán.
Tabla 13. Análisis sintáctico en expresiones
|
Subcategoría |
Elementos |
SP-4 (n=3) |
SP-5 (n=8) |
SA-4 (n=10) |
SA-5 (n=7) |
|
Operatoria |
Suma |
3 |
6 |
0 |
6 |
|
Resta |
0 |
0 |
0 |
1 |
|
|
Selección de operatoria |
0 |
0 |
0 |
0 |
|
|
No presenta operatoria |
0 |
2 |
10 |
0 |
|
|
Ubicación del dato desconocido |
Derecha |
0 |
0 |
0 |
0 |
|
Izquierda |
3 |
3 |
0 |
0 |
|
|
Selección de ubicación |
0 |
5 |
10 |
7 |
|
|
Representación del dato desconocido |
Letra x |
0 |
3 |
0 |
0 |
|
Letra distinta a x |
0 |
0 |
0 |
0 |
|
|
Figuras |
3 |
0 |
0 |
0 |
|
|
Lenguaje verbal |
0 |
5 |
10 |
7 |
|
|
Relación de desigualdad |
Mayor que (>) |
1 |
2 |
0 |
0 |
|
Menor que (<) |
1 |
1 |
0 |
0 |
|
|
Mayor o igual que (≥) |
0 |
0 |
0 |
0 |
|
|
Menor o igual que (≤) |
0 |
0 |
0 |
0 |
|
|
Múltiples relaciones de desigualdad |
0 |
0 |
0 |
0 |
|
|
Selección de relación de desigualdad |
1 |
5 |
10 |
7 |
Nota: Fuente propia de la investigación.
En cuanto a los significados en las tareas mixtas (Tabla 14), del mismo modo que en las tareas de resolver inecuación, encontramos el significado restrictivo sobre el comparativo.
El significado comparativo se encuentra solo en SA-5, a partir de la instrucción, ¿cuánto es lo máximo que puede medir? El significado restrictivo en todos los textos es evidenciado en tareas que solicitan, por ejemplo, da 2 posibles y, también, a partir de términos claves como ¿cuántas? o ¿cuántos?
Tabla 14. Cantidad de tareas con significados
|
Significado |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Comparativo |
0 |
0 |
0 |
1 |
|
Restrictivo |
1 |
8 |
5 |
6 |
|
No evidencia |
2 |
0 |
5 |
0 |
|
Total |
3 |
8 |
10 |
7 |
Nota: Fuente propia de la investigación.
En las tareas mixtas no se propone ninguna estrategia, evidenciamos solo la sugerencia de la estrategia empleo de balanza en el proyecto SP con 2 en cada curso.
En cuanto a la demanda cognitiva, en todos los textos observamos PCC y, solo SA-4, además del anterior, incorpora HM (ver Tabla 15).
Tabla 15. Cantidad de tareas según el nivel de demanda cognitiva
|
Demanda cognitiva |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Procedimiento con conexión (PCC) |
3 |
8 |
6 |
7 |
|
Hacer matemáticas (HM) |
0 |
0 |
4 |
0 |
|
Total |
3 |
8 |
10 |
7 |
Nota: Fuente propia de la investigación.
Respecto a los contextos (Tabla 16) identificamos mayor variedad, a diferencia de los otros dos tipos de tareas, aunque predomina el contexto científico asociado a la matemática, tal como sucedía en el resto de tareas.
Tabla 16. Cantidad de tareas con contextos empleados
|
Contextos |
SP-4 |
SP-5 |
SA-4 |
SA-5 |
|
Personal |
0 |
4 |
5 |
2 |
|
Ocupacional |
0 |
1 |
0 |
0 |
|
Social |
0 |
1 |
1 |
2 |
|
Científico |
3 |
2 |
4 |
3 |
|
Total |
3 |
8 |
10 |
7 |
Nota: Fuente propia de la investigación.
A continuación, discutimos los resultados previamente presentados sobre las características de tareas relativas a inecuaciones, procedentes del análisis de 206 tareas en textos escolares chilenos de 4.° y 5.° grado de primaria. Las tareas caracterizadas atienden a los objetivos curriculares propuestos, aunque evidenciamos el reducido carácter algebraico.
Los resultados dan cuenta de tres tipos de tareas: plantear inecuación, resolver inecuación y mixtas. Estas se corresponden con los objetivos propuestos en las directrices curriculares chilenas (Figura 1), observándose que el énfasis está en la resolución de inecuaciones (Tabla 2).
En las tareas sobre resolver inecuaciones y tareas mixtas, se observó un significado comparativo y restrictivo, predominando este último. Esto favorece un conocimiento en profundidad del concepto de inecuación (Paoletti et al., 2021). No obstante, hay un alto número en tareas de resolver inecuaciones en las cuales no se evidencia que se promueva explícitamente un significado (Tabla 8 y 14), solo se pide resolver la inecuación. Considerando las dificultades que manifiestan estudiantes de secundaria con respecto a la falta de conexión con los diferentes tipos de significados que se les reconocen a las inecuaciones (Ferretti et al., 2022; Paoletti et al., 2021), o que los estudiantes de primaria resuelven las inecuaciones como si fueran ecuaciones (Agencia de Calidad de la Educación de Chile, 2019), pareciera ser necesario explicitar los significados en los primeros cursos en los que se estudia esta temática. Por ejemplo, analizar todas las soluciones posibles, para así, hacer consciente al alumnado de las diferencias entre ecuaciones e inecuaciones.
Sobre las estrategias para resolver las inecuaciones, aunque ambos proyectos presentan, inicialmente, distintas estrategias de resolución, luego dejan a criterio del alumnado escoger una u otra (Tabla 9), y no se profundiza en su comprensión. Esto podría ser un obstáculo en el aprendizaje del alumnado, ya que investigaciones previas muestran que las dificultades surgen producto de conocimientos básicos deficientes para resolver inecuaciones (Botty et al., 2015).
Por otro lado, se observa una escasa variedad de estructuras en las expresiones empleadas en los textos escolares. Esto podría tener un impacto en la comprensión y uso de distintas estrategias de resolución y en el carácter algebraico de las tareas. La mayoría presentan estructura aditiva, donde el dato desconocido está a la izquierda del signo de desigualdad y se representa con letra x o alguna figura geométrica. Estudios anteriores recomiendan presentar tareas cuyas estructuras evidencien las propiedades aritméticas (p. ej., Blanton et al., 2011) o que favorezcan estrategias de resolución estructural y analítica, así promover un significado relacional del signo igual (Kieran y Martínez-Hernández, 2022; Radford, 2022), en nuestro caso, sería de los signos de desigualdad. Esto es crucial en el desarrollo del pensamiento algebraico, ya que lo caracterizamos como un tipo de pensamiento que permite percibir y razonar sobre estructuras algebraicas (Kieran, 2004). Coincidiendo con Vega-Castro (2012) creemos que es necesario dirigir la atención del alumnado a la estructura, teniendo como foco el desarrollo del sentido estructural, este último, entendido como la capacidad de: percibir, comparar y relacionar las estructuras de diversas expresiones y seleccionar procedimientos adecuados para utilizar en las mismas. A su vez, estaríamos promoviendo las prácticas de generalización y razonamiento sobre dichas generalizaciones, prácticas que no se observaron en los textos escolares.
Ahora bien, si nos centramos en la práctica de representar, evidenciada en las tareas de plantear inecuación y las mixtas. Se observa un predominio de las representaciones simbólicas alfanuméricas (Tabla 3 y 12). Radford (2018) señala que el pensamiento algebraico trata con cantidades desconocidas, pero estas pueden ser representadas de múltiples modos. A su vez, señala que el uso de simbolismo alfanumérico, por sí mismo, no es sinónimo de pensamiento algebraico, ya que dicho pensamiento requiere tratar las cantidades desconocidas de forma analítica. Esto, relacionado con lo mencionado previamente sobre las estructuras, nos hace pensar que las tareas analizadas carecen del carácter algebraico. En las tareas se solicita representar con símbolos alfanuméricos, pero no se razona sobre la estructura o las posibles transformaciones que se podrían realizar sobre estas.
Asimismo, en nuestro estudio describimos, por un lado, cómo se representan cantidades desconocidas en las tareas, y, por otro, cómo se representan las relaciones de desigualdad. Notamos que las cantidades desconocidas se constituyen, mayoritariamente, con la letra x y sin otorgarle sentido o significado. Investigaciones recientes recomiendan que, para que el alumnado piense de manera más sofisticada sobre la notación de variables es necesario apoyar la comprensión de los símbolos literales incluyendo el uso de términos del lenguaje natural como “muchos” o adverbios indeterminados (Ayala-Altamirano et al., 2022); tratar las cantidades desconocidas en contextos que permitan verbalizarlas de forma explícita o dibujarlas (Ellis y Ózgür, 2024). Sobre las relaciones de desigualdad, en las tareas se observa que, en algunas ocasiones, se recurre al lenguaje natural para darles significado, por ejemplo: inclinada al lado, aumentar, sin igualar, más que, mayor que, menos que, mayor o igual que, menor o igual que, por mencionar algunas; otro modo es desde la observación (visual) de lo que ocurre con la balanza. Las palabras máximo y mínimo son utilizadas para seleccionar la respuesta en el conjunto de soluciones y no para la relación de desigualdad.
Observamos un escaso trabajo de la práctica de justificar, la cual se sugiere para dar explicación y justificación de por qué la incógnita toma cierto valor, lo que Blanton (2017) identifica como una justificación de carácter aritmético. Esta autora señala que una justificación algebraica busca razonar sobre relaciones; por tanto, un aspecto a mejorar en las tareas de los textos escolares es el objetivo de esta práctica.
Los resultados obtenidos respecto a la demanda cognitiva son relevantes ya que evidencian que las tareas de plantear inecuación y mixtas promueven, en su mayoría, alta demanda cognitiva (PCC y HM), focalizadas en tareas con modos de representación y relaciones matemáticas. Las tareas de resolver inecuación conformadas por tareas con alta y baja demanda (PSC y PCC), son dirigidas a la reproducción de respuestas correctas y escasa evidencia de los procedimientos empleados. Smith y Stein (1998) señala que las tareas de alta demanda cognitiva orientan al estudiantado a un pensamiento más allá de lo algorítmico, fomentan la exploración y comprensión de los conceptos, procesos o relaciones matemáticas.
Son limitadas las tareas de hacer matemáticas y no se observan de memorización, ambas ubicadas en los extremos de la demanda cognitiva (alta y baja demanda, respectivamente). Por tanto, debemos proveer instancias donde el estudiantado logre desarrollar tareas en niveles de alta demanda cognitiva, los cuales contribuyan a que los sujetos transiten en diversos modos de representar, desarrollen esfuerzos cognitivos mayores, conecten conocimientos. Es importante tener en cuenta el currículo, que sugiere adaptar los niveles de aprendizaje para los distintos grupos de estudiantes. Por lo tanto, es imprescindible considerar la demanda cognitiva para cada uno de ellos.
En los contextos involucrados en los cuales son desarrolladas las tareas predomina el contexto científico. Damos cuenta de la baja presencia de contextos personal, social y ocupacional. De modo que contemplamos la propuesta PISA (OECD, 2022) la cual considera relevante la implementación de contextos que reflejen la realidad del sujeto, así como la diversidad de estos. En concordancia con el currículo, consideramos tareas en diversos contextos, las cuales son vinculadas con la vida real del estudiantado.
La investigación realizada permitió la caracterización de tareas de inecuación incluidas en textos escolares chilenos de 4.° y 5.° grado de primaria. Dicha caracterización refleja aspectos en relación con: las prácticas algebraicas, las estructuras, el significado de las inecuaciones, las estrategias de resolución, el nivel de demanda cognitiva y los contextos involucrados.
Destacamos el trabajo de la representación y justificación; sin embargo, creemos que estos hallazgos visibilizan la necesidad de conducir dichas prácticas hacia la generalización, así como el desarrollo de todas las prácticas, las cuales fomentan el desarrollo del pensamiento algebraico en el trabajo, con tareas de inecuación. La escasa variedad de expresiones restringe la capacidad de razonar acerca de las estructuras y, por tanto, no favorece el empleo de otras estrategias como la estructural y analítica. La presencia de significados comparativo y restrictivo produce mayor comprensión del concepto de inecuación. Debemos otorgar la oportunidad para que los estudiantes desarrollen habilidades más allá de lo algorítmico, por lo cual el trabajo con tareas de procedimiento con conexión y hacer matemáticas incentivan una mayor demanda cognitiva. Por último, es importante incorporar la diversidad de contextos que acerquen a la realidad del estudiantado, favoreciendo su capacidad de enfrentar tareas contextualizadas.
Nuestro trabajo amplía los hallazgos de la literatura vinculados a la inecuación, en concreto, en educación primaria, donde la inecuación y desigualdad han recibido menor atención en la investigación desde el pensamiento algebraico. Este estudio contribuye en la toma de decisiones en el nivel nacional e internacional en la confección de recursos como los textos escolares, y de utilidad para el profesorado, al contar con herramientas, específicamente, tareas de inecuaciones adecuadas para implementar en las salas de clases.
Ofrecemos un punto de partida para el tratamiento de dicho contenido en educación primaria, al considerar elementos como: el desarrollo del pensamiento algebraico y la conciencia desde la estructura del álgebra (Molina y Cañadas, 2018; Kieran y Martínez-Hernández, 2022) en coherencia con nuestro objeto de estudio, así como la atención a los significados, las estrategias de resolución, los niveles de demanda cognitiva y los contextos involucrados en las tareas.
Una línea abierta es caracterizar las tareas con desigualdades e inecuaciones en relación con el carácter algebraico que presenten en otros niveles. A futuro nos ocuparemos en analizar el pensamiento algebraico que podrían dominar e implementar los estudiantes con tareas de inecuaciones.
Se concluye necesario, enriquecer el diseño de tareas para la enseñanza de la inecuación, tomando como referencia las categorías propuestas para visualizar qué elementos pueden ser mejorados, así, también, aplicables en futuras investigaciones, como en textos de distintos países.
Financiación
ANID, Beca Doctorado en el Extranjero 72220116
Agradecimiento
Proyecto PID2020-113601GB-I00 financiado por MCIN/AEI/10.13039/501100011033. Las autoras desean agradecer al editor y a los revisores por su ayuda en la mejora del artículo.
Conflicto de intereses
Las autoras declaran no tener algún conflicto de interés.
Declaración de la contribución de los autores
Todas las autoras afirmamos que se leyó la versión final de este artículo. El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: E. P. 50 %, C. A. A. 30 % y M. M. 20 %.
Declaración de disponibilidad de los datos
Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente [E. P.], previa solicitud razonable.
Preprint
Una versión Preprint de este artículo fue depositada en:
https://zenodo.org/doi/10.5281/zenodo.8350067
Agencia de Calidad de la Educación (2019). Aprendiendo de los errores: Un análisis de los errores frecuentes de los estudiantes de 4º básico en las pruebas Simce y TIMSS y sus implicancias pedagógicas.
Ayala-Altamirano, C., Molina, M. y Ambrose, R. (2022). Fourth graders’ expression of the general case. ZDM Mathematics Education 54, 1377-1392 https://doi.org/10.1007/s11858-022-01398-8
Blanton, M. (2017). Algebraic reasoning in Grades 3-5. En M. Battista (Ed.), Reasoning and sense making in the mathematics classroom Grades 3-5 (pp. 67-102). NCTM.
Blanton, M., Brizuela, B., Stephens, A., Knuth, E., Isler, I., Gardiner, A., Stroud, R., Fonger, N. y Stylianou, D. (2018). Implementing a framework for early algebra. En C. Kieran (Ed.), Teaching and learning algebraic thinking with 5- to 12-year-olds: The global evolution of an emerging field of research and practice (pp. 27-49). Springer. http://doi.org/10.1007/978-3-319-68351-5_2
Blanton, M., Levi, L., Crites, T. y Dougherty, B. J. (2011). Developing essential understanding of algebraic thinking for teaching mathematics in Grades 3-5. NCTM.
Borello, M. (2010). Un planteamiento de resignificación de las desigualdades a partir de las prácticas didácticas del profesor: Un enfoque socioepistemológico. [Tesis doctoral, Centro de investigación en ciencia aplicada y tecnología avanzada. Instituto Politécnico Nacional].
Botty, H. M. R. H., Yusof, H. J. H. M., Shahrill, M. y Mahadi, M. A. (2015). Exploring students’ understanding on ‘inequalities.’ Mediterranean Journal of Social Sciences, 6(5), 218-227.
https://doi.org/10.5901/mjss.2015.v6n5s1p218
Carraher, D. W., Martínez, M. V. y Schliemann, A. D. (2008). Early algebra and mathematical generalization. ZDM Mathematics Education, 40, 3-22. https://doi.org/10.1007/s11858-007-0067-7
Castro, E., Rico, L. y Romero, I. (1997). Sistemas de representación y aprendizaje de estructuras numéricas. Enseñanza de las Ciencias, 15(3), 361-371. https://doi.org/10.5565/rev/ensciencias.4164
Christou, C., Pitta-Pantazi, D., Pittalis, M., Demosthenous, E. y Chimoni, M. (2023). Personalized mathematics and mathematics inquiry: A design framework for mathematics textbooks. En R. Leikin. (Ed.), Mathematical challenges for all. Research in Mathematics Education (pp. 71-92). Springer. https://doi.org/10.1007/978-3-031-18868-8_5
Ellis, A. B. y Özgür, Z. (2024). Trends, insights, and developments in research on the teaching and learning of algebra. ZDM Mathematics Education. 56, 199-210. https://doi.org/10.1007/s11858-023-01545-9
Fernández-Millán E. y Molina, M. (2016). Indagación en el conocimiento conceptual del simbolismo algebraico de estudiantes de secundaria mediante la invención de problemas. Enseñanza de las Ciencias, 34(1), 53-71. https://doi.org/10.5565/rev/ensciencias.1455
Ferretti, F., Santi, G. R. P. y Bolondi, G. (2022). Interpreting difficulties in the learning of algebraic inequalities, as an emerging macro-phenomenon in large scale assessment. Research in Mathematics Education, 24(3), 367-389. https://doi.org/10.1080/14794802.2021.2010236
Garrote, M., Hidalgo, J. y Blanco, L. (2004). Dificultades en el aprendizaje de las desigualdades e inecuaciones. Suma: Revista sobre Enseñanza y Aprendizaje de las Matemáticas, 46, 37-44.
Heredia, M. y Palacios, M. (2014). Las inecuaciones lineales en la escuela: Algunas reflexiones sobre su enseñanza a partir de la identificación de dificultades y errores en su aprendizaje. [Tesis de licenciatura]. Universidad del Valle. https://hdl.handle.net/10893/7743
Hernández-Sampieri, R. y Mendoza, C. (2018). Metodología de la Investigación. McGraw Hill.
Kaput, J. J. (2008). What is algebra? What is algebraic reasoning? En J. J. Kaput, D. W. Carraher y M. L. Blanton (Eds.), Algebra in the early grades (pp. 5-17). Lawrence Erlbaum Associates.
https://doi.org/10.4324/9781315097435-2
Kieran, C. (2004). Algebraic thinking in the early grades: What is it? The Mathematics Educator, 8(1), 139-151.
Kieran, C. y Martínez-Hernández, C. (2022). Structure sense at early ages: The case of equivalence of numerical expressions and equalities. En T. Rojano (Ed.), Algebra structure sense development amongst diverse learners (pp. 35-66). Routledge. https://doi.org/10.4324/9781003197867-3
Kirshner, P. (1989). The visual sintax of Algebra. Journal for Research in Mathematics Education 20(3), 274-287. https://doi.org/10.2307/749516
Lloyd, G., Herberl-Eisenmann, B. y Star, J. (2011). Expressions, equations, and functions: The big ideas and essential understandings. En R. M. Zbieck (Ed.), Developing essential understanding of expressions, equations, and functions Grades 6-8 (pp. 30-43). NCTM.
Martínez, S., Varas, L., López, R., Ortiz, A. y Solar, H. (2013). Álgebra para para futuros profesores de educación básica. SM. https://www.cpeip.cl/wp-content/uploads/2020/07/REFIP-Algebra_01.pdf
Mason, J. (2017). Overcoming the algebra barrier: Being particular about the general, and generally looking beyond the particular, in homage to Mary Boole. En S. Stewart (Ed.), And the rest is just algebra (pp. 97-117). Springer.
https://doi.org/10.1007/978-3-319-45053-7_6
Ministerio de Educación de Chile [MINEDUC]. (2012). Bases Curriculares de la Enseñanza de Educación Matemática. Unidad de Currículum y Evaluación. https://www.curriculumnacional.cl/614/articles-22394_bases.pdf
Ministerio de Educación y Formación Profesional [MEFP]. (2022). Real Decreto 157/2022 de 02 de marzo, por el que se establece la ordenación y enseñanzas mínimas de la Educación Primaria. BOE, 52, 24386-24504.
https://www.boe.es/eli/es/rd/2022/03/01/157
Molina, M. y Cañadas, M. C. (2018). La noción de estructura en el early algebra. En P. Flores, J. L. Lupiáñez e I. Segovia (Eds.), Enseñar matemáticas. Homenaje a los profesores Francisco Fernández y Francisco Ruiz (pp. 129-141). Atrio.
Mullis, I. V. S., Martin, M. O., Foy, P. y Arora, A. (2012). TIMSS 2011 international results in mathematics. TIMSS y PIRLS International Study Center.
National Governors Association Center for Best Practices and Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Council of Chief State School Officers. https://learning.ccsso.org/wp-content/uploads/2022/11/Math_Standards1.pdf
Ngu, B. H., Phan, H. P., Yeung, A. S. y Chung, S. F. (2018). Managing element interactivity in equation solving. Educational Psychology Review 30, 255-272 https://doi.org/10.1007/s10648-016-9397-8
OECD (2022). PISA 2022 Marco de Matemáticas. OECD. https://pisa2022-maths.oecd.org/#Contexts
Ontario Ministry of Education. (2020). The Ontario curriculum, Grades 1-8: Mathematics 2020. Queen’s Printer for Ontario.
https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics
Paoletti, T., Stevens, I. y Vishnubhotla, M. (2021). Comparative and restrictive inequalities. The Journal of Mathematical Behavior, 63, Article 100895. https://doi.org/10.1016/j.jmathb.2021.100895
Penalva, M. D. C. y Llinares, S. (2011). Tareas matemáticas en la educación secundaria. En J. M. Goñi (Ed.), Didáctica de las Matemáticas (pp. 27-51). GRAO.
Pino-Fan, L. R., Lugo-Armenta, J. G., Cardelas, G. R. A., García, J., Peña, C. y Uicab-Campos, Y. (2024). Conflictos potenciales identificados en los libros de texto de matemáticas de educación básica de Chile para el estudio del álgebra. Journal of Research in Mathematics Education, 13(1), 59-86. https://doi.org/10.17583/redimat.14137
Radford, L. (2018). The emergence of symbolic algebraic thinking in primary school. En C. Kieran (Ed.), Teaching and learning algebraic thinking with 5- to 12-year-olds (pp. 3-25). Springer Cham. https://doi.org/10.1007/978-3-319-68351-5_1
Radford, L. (2022). Introducing equations in early algebra. ZDM Mathematics Education 54, 1151-1167. https://doi.org/10.1007/s11858-022-01422-x
Rico, L. (2009). Sobre las nociones de representación y comprensión en la investigación en educación matemática, PNA 4(1), 1-14.
https://doi.org/10.30827/pna.v4i1.6172
Sievert, H., Van den Ham, AK. y Heinze, A. (2021). The role of textbook quality in first graders’ ability to solve quantitative comparisons: A multilevel analysis. ZDM Mathematics Education 53, 1417-1431. https://doi.org/10.1007/s11858-021-01266-x
Smith, M. S. y Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344-350. https://doi.org/10.5951/MTMS.3.5.0344
Stephens, A., Ellis, A., Blanton, M. y Brizuela, B. (2017). Algebraic thinking in the elementary and middle grades. En J. Cai (Ed.), Compendium for research in mathematics education. Third handbook of research in mathematics education (pp. 386-420). NCTM.
Thanheiser, E. y Sugimoto, A. (2022). Justification in the context of elementary grades: Justification to develop and provide access to mathematical reasoning. En K. Bieda, A. M. Conner, K. W. Kosko y M. Staples (Eds.), Conceptions and consequences of mathematical argumentation, justification, and proof (pp. 35-48). Springer. https://doi.org/10.1007/978-3-030-80008-6_4
Valverde, G. A., Bianchi, L. J., Wolfe, R. G., Schmidt, W. H. y Houng, R. T. (2002). According to the book: Using TIMSS to investigate the translation of policy into practice through the world of textbooks. Kluwer Academic Publishers.
https://doi.org/10.1007/978-94-007-0844-0_8
Vega-Castro, D. (2012). Perfiles de alumnos de educación secundaria relacionados con el sentido estructural manifestado en experiencias con expresiones algebraicas. [Tesis doctoral]. Universidad de Granada. http://hdl.handle.net/10481/31311
Warren, E. (2006). Comparative mathematical language in the elementary school: A longitudinal study. Educational Studies in Mathematics, 62(2), 169-189. https://doi.org/10.1007/s10649-006-4627-5
|
Proyecto |
Referencia |
|
SA-5 |
Alvarado, L. Carrero, M. y Caroca, M. (2021). Cuaderno de actividades de Matemática 5° básico (2.a ed.). Santillana. Alvarado, L., Carrero, M. y Caroca, M. (2022). Texto del estudiante. Matemática 5° básico (3.a ed.). Santillana. Catalán, M. (2021). Guía didáctica del docente matemática 5° básico, Tomo 1 (2.a ed.). Santillana. |
|
SA-4 |
Fuenzalida, A. y Cerda, V. (2021). Guía didáctica del docente matemática 4° básico, Tomo 2 (2.a ed.). Santillana. Fuenzalida, A., Freixas, A. y Cerda, V. (2022). Cuaderno de actividades Matemática 4° básico (3.a ed.). Santillana. Fuenzalida, A., Quezada, C. y Cerda, V. (2022a). Texto del estudiante. Matemática 4° básico (3.a ed.). Santillana. |
|
SP-4 |
Isoda, M. (2022). Sumo primero texto del estudiante, tomo 2, 4° básico (3.a ed.). Gakko Tosho Co, LTD. Isoda, M. (2022a). Sumo primero cuaderno de actividades, tomo 2, 4° básico (3.a ed.). Gakko Tosho Co, LTD. Isoda M. (2022b). Sumo primero guía didáctica docente, tomo 2, 4° básico (3.a ed.). Gakko Tosho Co, LTD. Isoda, M. (2022c). Sumo primero ticket de salida, 4° básico (3.a ed). Gakko Tosho Co, LTD. |
|
SP-5 |
Isoda, M. (2022d). Sumo primero texto del estudiante, tomo 2, 5° básico (3.a ed.). Gakko Tosho Co, LTD. Isoda, M. (2022e) Sumo primero cuaderno de actividades, tomo 2, 5° básico (3.a ed.). Gakko Tosho Co, LTD. Isoda M. (2022f). Sumo primero guía didáctica docente, tomo 2, 5° básico (3.a ed). Gakko Tosho Co, LTD. Isoda, M. (2022g). Sumo primero ticket de salida, 5° básico (3.a ed.). Gakko Tosho Co, LTD. |
1* Autora para correspondencia
Estefanía Pacheco,
 epacheco@correo.ugr.es,
epacheco@correo.ugr.es,  https://orcid.org/0009-0006-6528-3349
https://orcid.org/0009-0006-6528-3349Cristina Ayala-Altamirano,
 cristina.ayala@uma.es,
cristina.ayala@uma.es,  https://orcid.org/0000-0002-9165-9470
https://orcid.org/0000-0002-9165-9470Marta Molina,
 martamolina@usal.es,
martamolina@usal.es,  https://orcid.org/0000-0002-1213-6162
https://orcid.org/0000-0002-1213-6162Departamento de Didáctica de las Matemáticas, Facultad de Ciencias de la Educación, Universidad de Granada, Granada, España.
2 Departamento de Didáctica de las Matemáticas, Ciencias Sociales y Ciencias Experimentales, Universidad de Málaga, Málaga, España.
3 Departamento de Didáctica de las Matemáticas y de las Ciencias Experimentales, Facultad de Educación y Turismo de Ávila, Universidad de Salamanca, Ávila, España.
Caracterización de tareas sobre inecuaciones en libros de textos escolares en educación primaria (Estefanía Pacheco • Cristina Ayala-Altamirano • Marta Molina) Uniciencia is protected by Attribution-NonCommercial-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0)
URL: www.revistas.una.ac.cr/uniciencia
Correo electrónico: revistauniciencia@una.cr