Inferencia estadística en los textos escolares: una aproximación al pensamiento estadístico

Statistical Inference in School Textbooks. An Approach to Statistical Thinking

Inferência estatística em livros escolares: uma abordagem ao pensamento estatístico

Francisco Rodríguez-Alveal1*, Maitere Aguerrea2

Received: Sep/15/2023 • Accepted: Feb/26/2024 • Published: Jul/31/2024

Resumen [Objetivo] El presente estudio tuvo como objetivo principal analizar las actividades relacionadas con inferencia estadística, presentes en los textos escolares de enseñanza secundaria en Chile, y su relación con el desarrollo del pensamiento estadístico. [Metodología] Para efectos del estudio se hizo uso de un enfoque cualitativo mediante un análisis de contenido de los libros de enseñanza secundaria difundidos, gratuitamente, por el Ministerio de Educación chileno durante los años 2016, 2018, 2020, 2021 y 2022, los cuales fueron seleccionados mediante un muestreo no probabilístico del tipo intencionado. [Resultados] Entre los principales resultados obtenidos, la mayoría de las actividades afines a inferencia estadística en los libros analizados, son del tipo procedimental, relacionadas con el cálculo de intervalos de confianza, sin abordar la interpretación de estos en el contexto de la situación problema. Además, se observa una escasa presencia de actividades relacionadas con inferencia informal. Asimismo, las actividades e interpelaciones explicitadas en los libros de texto no hacen referencia a la formulación de hipótesis o conjeturas acerca de los datos muestrales, de manera que se oriente a la formulación de conclusiones hacia la inferencia estadística. [Conclusiones] Los hallazgos entregan evidencias que, a pesar de que los intervalos de confianza se encuentran dentro de las temáticas afines a inferencia estadística en los libros de texto, estas no se focalizan en la toma de decisiones en el nivel poblacional, más bien son tratados desde un vértice descriptivo. Palabras clave: Inferencia estadística; intervalos de confianza; libros de texto; pensamiento estadístico; profesores en formación Abstract [Objective] The main purpose of this study was to analyze the activities related to statistical inference present in secondary education textbooks in Chile, and their relationship to the development of statistical thinking. [Methodology] For the purposes of the study, a qualitative approach was used through a content analysis of the secondary education books disseminated free of charge by the Chilean Ministry of Education during the years 2016, 2018, 2020, 2021 and 2022, which were selected using intentional non-probabilistic sampling. [Results] Among the main results obtained, it was found that most of the activities related to statistical inference in the textbooks analyzed had to do with procedures related to the calculation of confidence intervals, without addressing their interpretation in the context of the problem. In addition, it was observed that there were few activities related to informal inference. Likewise, the activities and questions presented in the textbooks do not refer to the formulation of hypotheses or conjectures about the sample data made to guide the formulation of conclusions related to statistical inference. [Conclusions] The findings indicate that despite the fact that confidence intervals are among the topics related to statistical inference in the textbooks, these textbooks are not focused on decision-making at the population level, but rather on description. Keywords: Confidence intervals; statistical inference; statistical thinking; textbooks; prospective teachers. Resumo [Objetivo] O objetivo principal deste estudo foi analisar as atividades relacionadas à inferência estatística, presentes textos escolares do ensino médio no Chile, e sua relação com o desenvolvimento do pensamento estatístico. [Metodologia] Para efeitos do estudo, utilizou-se uma abordagem qualitativa através de uma análise de conteúdo dos livros do ensino secundário distribuídos gratuitamente pelo Ministério da Educação do Chile durante os anos de 2016, 2018, 2020, 2021 e 2022, que foram selecionados por meio de amostragem não probabilística do tipo intencional. [Resultados] Dentre os principais resultados obtidos, a maior parte das atividades relacionadas à inferência estatística nos livros analisados são do tipo processual, relacionadas ao cálculo de intervalos de confiança, sem abordar sua interpretação no contexto da situação problema. Além disso, há uma presença escassa de atividades relacionadas à inferência informal. Da mesma forma, as atividades e questões explicadas nos livros de texto não se referem à formulação de hipóteses ou conjecturas sobre os dados amostrais, de modo que a formulação de conclusões seja orientada para a inferência estatística. [Conclusões] Os resultados fornecem evidências de que, embora os intervalos de confiança estejam dentro dos tópicos relacionados à inferência estatística nos livros de texto, eles não se concentram na tomada de decisões em nível populacional, mas são tratados a partir de um vértice descritivo. Palavras-chave: Inferência estatística; intervalos de confiança; livros de texto; pensamento estatístico; professores em formação

Introducción

La inferencia estadística es uno de los tópicos introducidos recientemente en el currículo escolar de enseñanza secundaria, a nivel mundial, siendo el objetivo principal que el estudiantado desarrolle comprensión y habilidades para aplicar nociones básicas de inferencia estadística, tanto acerca de pruebas de hipótesis como estimaciones puntuales y probabilísticas (GAISE, 2016), también, habilidades propias del pensamiento estadístico, como, por ejemplo, identificar los métodos inferenciales apropiados para una o dos muestras y comunicar conclusiones apropiadas a partir de inferencias (Wild y Pfannkuch, 1999; Garfield y Ben-Zvi, 2008); siendo las pruebas de hipótesis cruciales para la toma de decisiones en muchos campos del saber, como por ejemplo, en medicina, biología, economía, ingeniería y en educación (Shi y Yin, 2021).

No obstante, en general, a nivel mundial la inferencia estadística tiende a introducirse en el último año de la educación secundaria y en cursos introductorios en las instituciones de educación superior, situación que no es ajena al caso chileno (Pfannkuch, Wild y Parsonage, 2012); asumiendo que el estudiantado debió adquirir un repertorio conceptual, como el mencionado anteriormente, donde una componente importante en este proceso inferencial es el pensamiento probabilístico (Makar y Rubin, 2009). En este camino, pese a que la decisión de cuándo introducir la inferencia estadística en el trayecto formativo depende de variados factores, incluidos los objetivos del currículo, las habilidades y niveles de desarrollo del alumnado, algunos expertos sugieren que la inferencia estadística puede ser introducida, de manera informal, en etapas tempranas, como en los grados intermedios o incluso antes, al adaptar los conceptos a la comprensión del estudiantado, contextualizada a la vida real, en problemas prácticos, que le permitan llegar a conclusiones significativas y satisfactorias (Watson et al., 2018).

En este contexto, diversos autores, entre los que se encuentran Harradine, Batanero y Rossman (2011), han entregado evidencias de lo complejo que es este contenido, y que el estudiantado suele tener concepciones erradas y dificultades en la interpretación de conceptos como parámetros, estadígrafos, distribuciones muestrales, tipos de hipótesis y nivel de significación, entre otros. En este camino, para abordar esas dificultades, Borovcnik (2022) sugiere que “las reformas curriculares deben centrarse en el papel clave de la probabilidad condicional para todas aproximaciones a la inferencia estadística y en una sólida comprensión de la probabilidad dentro de una interpretación de la inferencia estadística” (p. 1).

Producto de lo anterior, esta investigación se centró en analizar las actividades presentes en los textos escolares de enseñanza secundaria en Chile, relacionadas con inferencia estadística, y si estas se enfocan en desarrollar habilidades propias al pensamiento estadístico en el estudiantado. Para responder a este objetivo general se plantearon los siguientes objetivos específicos: 1) Analizar la formulación de las actividades relacionadas con inferencia formal e informal presentes en los libros de texto; y 2) Determinar la relación de las actividades sobre inferencia estadística en los textos escolares con el pensamiento estadístico.

Marco teórico

Inferencia estadística y pensamiento estadístico

La inferencia estadística es definida por Collins (2003) como un conjunto de métodos para realizar juicios sobre los parámetros de una población con base en muestras probabilísticas. En cambio, para Moore (2004) la inferencia estadística “va más allá de los datos disponibles para sacar conclusiones sobre un universo más amplio, teniendo en cuenta que la variación está en todas partes y las conclusiones son inciertas” (p. 117). En esta misma línea en GAISE (2016), la inferencia estadística “consiste en obtener conclusiones sobre una población a partir de la información presente en una muestra. A menudo, esto implica el cálculo de estadísticas de la muestra para hacer inferencias sobre los parámetros de la población” (p. 11), mediante intervalos de confianza o pruebas de hipótesis. Por su parte, Makar y Rubin (2009) identifican en el proceso de la inferencia estadística participación de: a) una declaración de generalización “más allá de los datos”, b) uso de datos como evidencia para apoyar esta generalización, y c) lenguaje probabilístico (no determinista) que expresa cierta incertidumbre sobre la generalización (Figura 1). En los cuales, resalta la importancia de la variabilidad y la toma de decisiones en un escenario de incertidumbre, y la selección de modelos y procedimientos adecuados para el análisis estadístico de los datos; la interpretación de los resultados, según la situación contextual (Ben-Zvi y Makar, 2016); y la comunicación y evaluación crítica de resultados.

Lo anterior se encuentra en estrecha relación con el pensamiento estadístico (Garfield y Ben-Zvi, 2008), entendiéndolo como una habilidad cognitiva que implica la capacidad de comprender, interpretar y aplicar conceptos estadísticos en diversos contextos. Va más allá de la simple manipulación de datos numéricos, abarcando la comprensión de la variabilidad inherente a los fenómenos, la evaluación de la incertidumbre y la toma de decisiones informada basada en evidencia probabilística, capacitando a las personas para enfrentar la complejidad de los datos y utilizarlos de manera efectiva en la resolución de problemas (Sabbag et al., 2018).

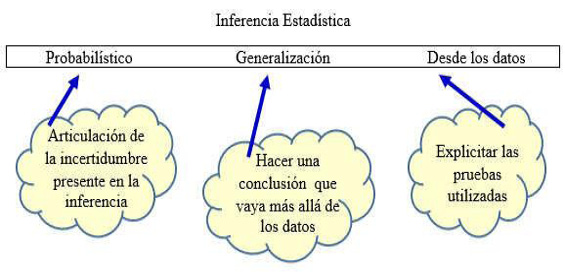
Figura 1. Un marco para el pensamiento acerca de la inferencia estadística (Makar y Rubin, 2009, p. 85)

En Chile, las investigaciones relacionadas con inferencia estadística son escasas, en particular Ruz et al. (2021), en un estudio realizado a 269 profesores en formación matemática encontraron evidencias de asociaciones descendidas entre el conocimiento y las actitudes hacia el contenido estocástico, en particular hacia la inferencia estadística. Antecedentes que son ratificados en la Evaluación Nacional Diagnóstica aplicada a los profesores en formación matemática, donde uno de los tópicos con menor porcentaje de logro es el relacionado con inferencia estadística (MINEDUC-CPEP, 2020). En esta misma línea Giaconi et al. (2022), en una pesquisa de carácter cualitativa, entregan antecedentes que evidencian que los profesores, en formación matemática, presentan dificultades en el aprendizaje y la enseñanza de la inferencia estadística a nivel de sistema escolar.

Intervalos de confianza y TICS

Los intervalos de confianza según Engel (2010) son uno de los conceptos más complejos en las asignaturas de estadística, cuya interpretación frecuentista establece que un intervalo de confianza del (1-α)100%, se caracteriza por un proceso de generar intervalos con la propiedad que cuando se repite el proceso varias veces, el (1-α)100 % de ellos contendrá al parámetro cuyo valor es desconocido, donde (1-α) se denomina nivel de confianza. Al respecto, muchos autores recomiendan el uso de intervalos de confianza como un complemento de las pruebas de hipótesis en la inferencia estadística (Reichardt y Gollob, 1997).

En coherencia con lo anterior, en el nivel de enseñanza secundaria, en el caso chileno, se introducen intervalos de confianza para el parámetro promedio poblacional (µ), asumiendo que los datos en el nivel poblacional se modelan mediante la distribución normal. En tal caso, a partir de la distribución de muestreo del promedio muestral, conociendo la varianza poblacional, haciendo uso de sus propiedades, colocando en juego el error entre el promedio verdadero y el muestral, y algunas manipulaciones algebraicas, el intervalo de confianza del 95 % para el promedio verdadero, tiene la forma de 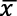± 1.96 𝜎 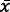, donde 𝜎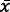, es el error de muestreo o error estándar del promedio muestral. Es decir, el error producido al estimar un parámetro mediante datos muestrales, donde el tamaño muestral tiene un efecto en dicho estadístico. Así, si el tamaño de la muestra crece (n → ∞), el error de muestreo tiende a cero (𝜎 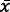→ 0); en términos probabilísticos se tiene que la

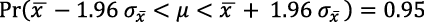
En esta misma línea, como menciona Reaburn (2014), las y los estudiantes deben comprender que las distribuciones muestrales se caracterizan por distribuirse, normalmente, acorde al teorema del límite central, donde aproximadamente el 95 % de ellas se encontrarán dentro de dos errores de la media poblacional; sumar y restar dos errores estándar producirá un rango de valores que incluirá el valor verdadero de la media poblacional.

En este camino, como se indica en GAISE (2016), el uso de herramientas tecnológicas como Excel o GeoGebra, presentes en el currículo escolar chileno, permitiría que el estudiantado explore los conceptos asociados con los intervalos de confianza, como nivel de confianza, error de muestreo, como así también, las nociones y propiedades subyacentes a ellos (Batanero et al., 2005).

Por otra parte, Meletiou-Mavrotheris, Lee y Fouladi (2007) no encontraron diferencias significativas entre un entorno de instrucción tradicional y uno tecnológico en la comprensión de los conceptos relacionados con inferencia estadística. Asimismo, Fidler y Cumming (2005) entregan antecedentes donde se expone que estudiantes de pregrado de psicología presentan conceptos erróneos acerca de los intervalos de confianza, como, por ejemplo, suponer que los intervalos de confianza se asocian con estadística descriptiva, asumiendo que ellos proporcionan valores plausibles de la media muestral, lo que implica que no se visualiza su naturaleza inferencial.

La inferencia estadística desde una mirada pedagógica

Recientemente en la literatura especializada se ha introducido el concepto de inferencia estadística informal (sus siglas en ingles ISI). Enfoque teórico y pedagógico para desarrollar el pensamiento y razonamiento estadístico a partir de los datos, conectando ideas estadísticas claves, como por ejemplo población, muestreo, parámetro, estadístico y aspectos informales del aprendizaje de la inferencia estadística, elaborando conclusiones tomadas de los datos, para inferir acerca del comportamiento en la población (Garfield y Ben-Zvi 2008).

En esta línea, Pfannkuch (2006) define la inferencia informal como “la extracción de conclusiones a partir de datos que se basan principalmente en observar, comparar y razonar a partir de distribuciones de datos” (p. 1). Asimismo, (Makar y Rubin, 2009), observan que, en la ISI, las generalizaciones toman como base la estructura de los datos, en cuyas extrapolaciones hacen uso de la incertidumbre, mediante un lenguaje probabilístico y procedimientos estadísticos no formales.

Al respecto, Alveal y Rubilar (2012) entregan evidencias que los profesores del sistema escolar chileno, al descodificar representaciones gráficas, no realizan lecturas más allá de los datos. Es decir, no efectúan extrapolaciones intuitivas hacia la población objeto de estudio, teniendo presente que dichas inferencias no son absolutas, jugando un rol fundamental el lenguaje, en el cual se debe enfatizar en un léxico probabilístico; en contraste, con la inferencia estadística formal, donde juegan un rol fundamental las estimaciones puntuales, el uso de intervalos de confianza y las pruebas de hipótesis.

Por lo tanto, desde una mirada pedagógica, este enfoque debería llevar a repensar la introducción de los tópicos relacionados con inferencia estadística en el currículo escolar, así como, en la formación de profesores de matemática (Garfield y Ben-Zvi 2008).

Metodología

Para lograr los objetivos de esta investigación, se realizó un muestreo no probabilístico del tipo intencionado (McMillan y Schumacher, 2011), permitiendo seleccionar un total de 3 libros de texto para la enseñanza secundaria en Chile (TE1, TE2, TE3), ofrecidos durante los años 2016, 2018, 2020, 2021 y 2022. Cabe destacar que algunos de estos han sido reediciones de la edición original, por lo cual, para efectos del presente estudio, se considerará solo el último año de edición (Tabla 1). Para mayor precisión, en el análisis de TE1 se considerará la edición del año 2020; de TE2 la del año 2020; y del libro de texto TE3 la edición del año 2022.

Tabla 1. Libros de texto del estudiante seleccionados de la muestra

Código	Autores/Año/Título/Editorial
TE1	Saiz, O., Blumenthal, V., (2016; 2018; 2020). Texto del estudiante, Matemática 3 año medio, Editorial Cal y Canto.
TE2	Muñoz, G., Gutiérrez, V., Muñoz, S., (2016; 2018; 2020). Texto del estudiante, Matemática 4 año medio, Santillana.
TE3	Osorio G., Norambuena, P., Romante, M., Gaete, D., Díaz, J., Celedón, J., Morales, K., Ortiz, N., Ramírez, P., Barrera, R., Hurtado, Y. (2021; 2022). Texto del estudiante, Matemática 3-4 medio, Editorial S. M.

Fuente: Elaboración propia.

El análisis de contenidos de los libros de texto se basó en la propuesta de Mayring (2000) y Cobo (2003), permitiendo orientar la investigación como sigue: primero, se seleccionaron los libros de textos que serían analizados; luego, se escogieron los capítulos en los cuales se hacía mención al concepto inferencia estadística; y, finalmente, se analizaron los conceptos, actividades y sus alcances con las habilidades y conocimientos relacionados con el pensamiento estadístico, tales como, habilidad para la formulación de preguntas estadísticas, recopilación y planificación de datos, comprensión de la variabilidad, pensamiento probabilístico, toma de decisiones bajo incertidumbre, conexión con problemas del mundo real, evaluación crítica de información y comunicación efectiva (Garfield y Ben-Zvi, 2008). Además, se contrastó con los lineamientos entregados por el informe GAISE (2016), como, por ejemplo “sacar conclusiones sobre una población a partir de la información contenida en una muestra, calcular un intervalo de confianza y comprender sus conceptos subyacentes a la inferencia y desarrollar un pensamiento estadístico” (p. 11).

Para el levantamiento de los datos, se realizó una matriz en Excel en la cual se identificaron las actividades de enseñanza aprendizaje e interpretación, análisis y visualización de datos, con sus respectivas preguntas e instrucciones (unidades de análisis) que estuviesen vinculadas al foco de la investigación. El código utilizado para presentar dichas unidades es: [Texto Escolar N.°, año, número de página en el texto escolar; número correlativo de actividades dentro del total del corpus].

Análisis y resultados

Inferencia estadística informal presente en los libros de texto

La inferencia estadística informal tiene por objetivo ir más allá de los datos, siendo la primera aproximación para realizar extrapolaciones con base en datos muestrales acerca de la población objeto de estudio (Makar y Rubin, 2009). Por ejemplo, conocida la edad promedio de una muestra, podemos inferir acerca de la edad promedio de la población de la cual se obtuvo la muestra. En este contexto, en los libros de texto analizados existe una escasa presencia de situaciones problemas, en los cuales el estudiantado debe responder preguntas que deben ir más allá de los datos (ISI). Para precisar, del total de la muestra de estudio se distinguieron 43 actividades con 76 preguntas relacionadas con inferencia estadística; de las cuales, solamente 7 (16,3 %) se relacionan con inferencia estadística informal, donde solo 3 de estas presentan situaciones afines a diseños experimentales, comparando datos de 2 grupos sometidos a diferentes tratamientos, siendo 1 de los tipos de inferencia estadística (Cobb, 2007). Se observa que estas actividades solo se presentan en el libro de texto de tercer año medio (TE1, 2020) mediante 14 interpelaciones en las cuales el estudiando debe dar respuesta a interrogantes afines a ISI. A manera de ejemplo, se muestran algunas de ellas:

Si desea que el tamaño de sus plantas sea homogéneo, ¿debe agregar fertilizante en sus plantas? Argumenta. [TE1, 2020, 18, 60]

¿Deberá preocuparse el jefe de operaciones del banco por la cantidad de empleados que se necesitará el mes siguiente? ¿qué decidirá? [TE1, 2020, 18, 53]

Si una persona quiere comprar, entre estos automóviles, el que brinde mayor seguridad, ¿qué decisión debería tomar? Explica. [TE1, 2020, 14, 61]

Situaciones en las cuales el estudiantado debería extrapolar o realizar predicciones e inferencias a partir de los datos muestrales entregados sobre información, que no se refleja directamente en ellos, de manera que pueda tomar decisiones en el nivel poblacional, es decir, “a partir de lo que ya se conoce, inferir sobre un suceso” (Alvarado et al., 2018, p. 136); acorde a lo mencionado en el tercer nivel de la taxonomía de Curcio (1989), relacionada con, leer más allá de los datos. Al respecto, este tipo de preguntas requieren un mayor nivel de conocimientos y del uso de un léxico estadístico, que permita hacer un puente entre lo descriptivo y lo inferencial, con base en un lenguaje probabilístico relacionado con el significado intuitivo de la probabilidad (Batanero, 2005) teniendo presente la aleatoriedad y la variabilidad presente en los datos. En síntesis, se requiere haber adquirido habilidades relacionadas con el pensamiento estadístico (Garfield y Ben-Zvi, 2008), en el cual deberían explorar, interpretar y obtener conclusiones, habilidades relacionadas con las fases análisis y conclusión del ciclo investigativo de Wild y Pfannkuch (1999), respectivamente.

Inferencia estadística formal presente en los libros de texto

En los libros de texto analizados (Tabla 1) se distinguieron 43 actividades, que contienen 62 preguntas relacionadas con métodos estadísticos afines a inferencia estadística formal. Al respecto, del total de los casos presentes, solamente 36 (83.7 %) se relacionan con la construcción y conceptos relacionados con el cálculo de intervalos de confianza (IC) como, por ejemplo, error de muestreo, cálculo de tamaño de muestra, y nivel de confianza, entre otros.

Usualmente, las interpelaciones realizadas en los libros de texto estudiados hacen uso indistintamente del verbo transitivo “determinar” (10 repeticiones) y del pronombre interrogativo “cuál” (11 repeticiones), asociadas a requerimientos donde el estudiantado, en general, debe construir un intervalo de confianza con base en la información entregada en el enunciado de la actividad, sin interpretarlo en el contexto de la situación problema ficticia presentada, o sea, se evidencia una tarea de aprendizaje esencialmente procedimental. Algunos ejemplos al respecto son:

Determina un intervalo de confianza para la media con un nivel de confianza del 95% [TE2, 2020, 322, 1]

Determina el intervalo de confianza en el que se encuentre la cantidad promedio de artículos defectuosos por caja, considerando un nivel de confianza del 90% [TE2, 2020, 322, 2]

¿Cuál es el intervalo de confianza al 95% para el gasto promedio de útiles escolares durante un año académico? [TE2, 2020, 325, 17]

Determina el intervalo de 90% de confianza para el número medio de horas diarias que ven televisión los niños de esa ciudad. [TE2, 2020, 325, 14]

Se evidencia, que solamente en una de las preguntas se hace referencia, de manera implícita, a que el intervalo de confianza permitiría extrapolar, hacia la población objeto de estudio, el comportamiento del promedio de las horas que los niños ven televisión. Asimismo, este tipo de preguntas fomentan el uso algorítmico de los métodos estadísticos y obstaculizan la adquisición de procedimientos adecuados para el análisis de los datos e interpretación de los resultados, según la situación contextual; y, en consecuencia, para desarrollar un pensamiento estadístico (Garfield y Ben-Zvi, 2008). Lo que podría implicar un desarrollo deficiente de conceptos y procedimientos estadísticos, declarados en el currículo escolar, en coherencia con lo evidenciado por Batanero et al., (2013).

Por otro lado, también se observa en los libros de textos preguntas en las cuales se pide analizar el efecto del tamaño muestral y el nivel de confianza en la amplitud del intervalo de confianza, así como también, la incidencia del nivel de confianza en el tamaño muestral, como se muestra a continuación:

Si aumentamos el tamaño de la muestra, sin variar el nivel de confianza, la amplitud del intervalo de confianza, ¿aumenta o disminuye? Justifica tu respuesta. [TE2, 2020, 323, 5]

Si aumentamos el intervalo de confianza a un 98%, sin cambiar el tamaño de la muestra, la amplitud del intervalo de confianza, ¿aumenta o disminuye? Justifica [TE2, 2020, 323, 6]

¿Qué ocurre con los límites del intervalo a medida que el tamaño de la muestra aumenta? [TE2, 2020, 184, 62]

¿Qué ocurre con el tamaño muestral si se aumenta el nivel de confianza a un 99% manteniendo el margen de error? Justifica [TE2, 2020, 324, 11]

Preguntas en las cuales el estudiantado, de manera empírica, debe estudiar el efecto que tiene el tamaño de la muestra y el nivel de confianza en la amplitud del intervalo de confianza, es decir, analizar la expresión 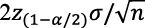cuando n → ∞, atendiendo lo que se explicita en el informe GAISE (2005) “el tamaño de la muestra tiene influencia sobre el efecto de variabilidad de la muestra (error)” (p. 11); así como también, estudiar el efecto del tamaño muestral en el nivel de confianza (z(1 – 𝛼/2)), mediante simulaciones numéricas o computacionales, que pueden ser realizadas, por ejemplo, con los softwares Excel o GeoGebra. Al respecto, se está en coherencia con Giaconi et al. (2022) pues este tipo de tareas “generan oportunidades de aprendizaje” (p. 78) ahondando en cuestiones conceptuales acorde a los lineamientos dados en el informe GAISE (2016).

Por otro lado, también se observan actividades donde se insta a calcular un tamaño muestral bajo ciertos escenarios, como se muestra a continuación:

Por estudios previos se sabe que la desviación estándar del número de horas que corre una persona diariamente es 0,3. Para realizar la estimación al 95% de confianza con un margen de error máximo de 0,01, ¿cuál es el tamaño necesario de la muestra? [TE2, 2020, 324, 11]

¿Qué tamaño muestral se necesitaría si se considera un margen de error igual al considerado en la pregunta a), y un nivel de confianza igual al de la pregunta b? [TE2, 2020, 325, 16]

¿Cuántos datos son suficientes para estimar, con una confianza del 95%, la masa media de esta población con un error no superior a 15 g? [TE2, 2020, 326, 30]

Una población se distribuye en forma normal. ¿Qué tamaño debe tener la muestra para que, con un nivel de confianza del 90%, el error estándar no supere 90? [TE2, 2020, 327, 34]

Interpelaciones donde el estudiantado debe conectar ideas y conceptos estadísticos como error o margen de error y nivel de confianza. Conceptos definidos, explícitamente, en los libros de texto analizados, al introducir la expresión para el intervalo de confianza, para el promedio verdadero o para calcular un tamaño de una muestra, bajo ciertas condiciones. No obstante, se observa que no se solicita explicar los procesos que hay detrás de las respuestas a las preguntas realizadas, así como, justificar la selección de modelos y procedimientos realizados para el análisis estadístico de los datos, fortaleciendo las habilidades asociadas al pensamiento estadístico (Wild y Pfannkuch,1999; Garfield y Ben-Zvi, 2008).

Inferencia estadística formal e informal y su relación con el pensamiento estadístico

En la Tabla 2 se vinculan las habilidades y conocimientos presentes en las preguntas afines al concepto de inferencia estadística informal y formal presentes en los libros de texto analizados, acorde al marco propuesto por Wild y Pfannkuch (1999), en relación con el ciclo investigativo (PPDAC), el cual es coherente con Garfield y Ben-Zvi (2008).

Tabla 2. Habilidades y conocimientos acerca del pensamiento estadístico presente en las preguntas según libros de texto analizados

			Habilidades/conocimientos	Inferencia Estadística Informal (ISI)			Inferencia Estadística Formal
				TE1	TE2	TE3	TE1	TE2	TE3
	Tipos de pensamiento estadístico Will y Pfannkuch (1999)		Reconocimiento de la necesidad de los datos
			Transnumeración
			Percepción de la variación	x				x
			Razonamiento de modelos
			Integración de la estadística y el Contexto					x	x
	Ciclo Investigativo		Planteamiento del problema y preguntas					x	x
			Planificación y diseño
	PPDAC Will y Pfannkuch (1999)		Datos: Recolección de datos
			Análisis descriptivo e inferencial de los datos
			Conclusión: Interpretación y comunicación					x	x
Garfield y Ben-Zvi (2008)			Evaluación crítica de los resultados	x
			Lenguaje estadístico	x				x	x

Fuente: Wild y Pfannkuch (1999), Garfield y Ben-Zvi (2008)

Como se puede apreciar en la Tabla 2, solamente el libro de texto de tercer año de secundaria (TE1, 2020) presenta actividades relacionadas con estadística inferencial informal, en las cuales el estudiantado interactúa con el concepto variabilidad; habilidad que se relaciona con la percepción de la variabilidad, siendo este un tipo de pensamiento estadístico (Wild y Pfannkuch, 1999). A continuación, se muestran algunos ejemplos:

¿Qué ocurriría con la dispersión de los datos si las temperaturas se tomaran en distintas estaciones del año? Justifica [TE1, 2020, 14, 52]

¿Qué ocurrirá con la dispersión de los datos si las temperaturas se tomaran en distintas estaciones del año? Justifica [TE1, 2020, 14, 55]

Con los resultados anteriores, ¿qué decisión debe tomar el profesor? Argumenta tu respuesta. [TE1, 2020, 17, 56]

Al respecto, se observa que en el libro de texto TE1, se usa la palabra dispersión como sinónimo de variación, lo cual ha sido también reportado en la investigación de Rodríguez-Alveal y Maldonado-Fuentes (2023); sin embargo, para Reading y Shaughnessy (2004) estos son dos conceptos diferentes, situación que, eventualmente, influiría en la interpretación de los resultados. Atendiendo que variación es un sustantivo que se usa para describir el acto de variar o cambiar una condición (Ben-Zvi y Garfield, 2004; 201).

De manera similar, en las actividades afines a inferencia estadística formal, el estudiantado debe dar respuesta a interrogantes asociadas a la variabilidad de los datos, puntualmente el efecto del parámetro desviación estándar en la amplitud del intervalo de confianza y en el error estándar o error de muestreo, como se muestra a continuación:

Al escoger otra población con una desviación estándar mayor, ¿qué ocurre con la amplitud del intervalo si mantenemos el tamaño de la muestra? [TE2, 2020, 21, 325]

¿Patricio dice que, si tenemos dos poblaciones con diferentes desviaciones estándar, y en ambas extraemos una muestra del mismo tamaño, podemos saber de antemano en cuál el error estándar será mayor? ¿Estás de acuerdo con Patricio?, ¿por qué? [TE2, 2020, 23, 325]

En estas actividades se solicita realizar una evaluación crítica de los resultados, a fin de tomar una decisión con base en los datos muestrales; recurriendo a habilidades asociadas al pensamiento estadístico (Garfield y Ben-Zvi, 2008).

En relación con el planteamiento del problema y preguntas (fase del ciclo investigativo de Wild y Pfannkuch (1999)), se observa que, en su redacción no se da cuenta si el contexto y los datos son reales, producto de lo cual, desde la mirada de los autores presentan una “pseudo-contextualización” (León, 2021; p. 237). A manera de ejemplo, se presentan los siguientes enunciados de las actividades del libro de texto TE2 y TE3 respectivamente:

El dueño de una farmacia se encuentra interesado en saber si el refrigerado en que se conservan las vacunas ha mantenido la temperatura media de 5,5oC durante los meses recientes. De no ser así deberá comprar otro para no afectar la durabilidad y efectividad de las vacunas. [TE3, 2020, 183, 68]

Para estudiar el consumo de leche, en litros por persona al mes, se ha elegido una muestra de 150 personas cuyo consumo medio es de 22 L. Si dicho consumo sigue una distribución normal cuya desviación estándar es 6 L, determina un intervalo de confianza para la media con un nivel de confianza del 95%. [TE2, 2020, 322, 1]

Se hace un experimento exponiendo a un antibiótico una muestra aleatoria de 50 bacterias, las que demoran un tiempo promedio de 30 horas en morir. Si en la población ese tiempo se distribuye N(µ, 5). Determinar un intervalo de confianza al 95% para el tiempo promedio de muerte de las bacterias expuestas a dicho antibiótico. [TE3, 2022,191, 75]

En las cuales no se explicita si el enunciado y los datos fueron extraídos de alguna publicación científica o informe técnico, lo que lleva a pensar a los autores que es ficticio. Situación que no es coherente a lo mencionado por el informe GAISE (2016), acerca del uso de datos reales y contextualizados en la enseñanza de la estadística.

Por otra parte, y respecto al lenguaje utilizado, en general, en los libros de texto de la muestra de estudio, aspecto importante del pensamiento estadístico a considerar según Garfield y Ben-Zvi (2008), las actividades presentadas afines a inferencia estadística formal, hacen mención de estadísticos y parámetros como el promedio, desviación estándar y varianza. Cabe hacer notar que se utiliza, de manera indistinta, el concepto promedio y promedio muestral para hacer referencia a la media aritmética; conceptos claves para el análisis inferencial; lo cual, podría generar obstáculos en el estudiantado; esto, porque la inferencia estadística implica hacer afirmaciones sobre la población, basándose en información de una muestra, y si el estudiantado no reconoce la diferencia entre la media muestral y la poblacional, puede malinterpretar los resultados y no comprender completamente los conceptos claves de la inferencia, como los intervalos de confianza y las pruebas de hipótesis.

Finalmente, en relación con los intervalos de confianza, se hace mención de conceptos y expresiones simbólicas mediante representaciones algebraicas del nivel de confianza, tamaño muestral, amplitud y error estándar, desde una mirada esencialmente procedimental, los cuales son definidos, en algunos casos, en los márgenes de los libros de texto analizados. Es decir, se entregan las fórmulas, asociadas a las expresiones mencionadas, para que el estudiantado pueda calcular el intervalo de confianza para el promedio verdadero. Sin embargo, los conceptos margen de error y nivel de significación (𝛼) no son abordados, aunque este último se invisibiliza con el concepto nivel de significación. Lo cual puede ser explicado debido a que los libros de texto no abordan el contraste de hipótesis, sino que los intervalos de confianza tienen la misma interpretación frecuencial de los contrastes de hipótesis (Batanero, 2013).

Conclusiones

La inferencia estadística es una de las temáticas recientemente introducidas en el currículo escolar chileno y desde el año 2022, acorde con una reestructuración del currículo, en el cual se aborda en electivos de profundidad en el nivel de enseñanza secundaria. En este contexto, es de interés conocer cómo se introduce este concepto, dado que una de las sugerencias del GAISE (2016) es generar un pensamiento estadístico en el estudiantado; en tal caso, las actividades deberían movilizar conceptos y habilidades fundamentales acorde a lo mencionado por Wild y Pfannkuch (1999), Garfield y Ben-Zvi (2008), tales como, habilidad para recopilar, organizar y representar datos; comprender el concepto de probabilidad y sus diferencias con la estadística; habilidad para estimar parámetros y hacer prueba de hipótesis, diferenciando entre población y muestra; interpretar resultados y ser críticos fundamentados; uso de tecnología para el manejo de datos; y comunicar y argumentar basados en datos.

De acuerdo con los resultados del estudio se desprende que el concepto de inferencia estadística informal (ISI) es abordado solamente en el libro de texto de tercer año de secundaria (TE1, 2020), con la presencia de cuatro actividades, situación insuficiente atendiendo que ha sido sugerido por Rossman (2008) y el informe GAISE (2016), entre otros. Además, cabe hacer notar que, en dichas actividades y las correspondientes preguntas, no interpelan al estudiantado a formular hipótesis o conjeturas acerca del comportamiento estocástico del fenómeno en la población objeto de estudio, de manera de ir más allá de una interpretación descriptiva de los datos, lo cual Huerta (2020) ha denominado conjeturar-argumentar “para convencer de la bondad de una conjetura y no para demostrar su verdad” (p. 81); considerando que la ISI permite introducir conceptos e “ideas fundamentales que sustentan la comprensión de la inferencia estadística formal” (Batanero, 2013, p. 7). Lo que, además, no ha sido replicado en las actividades del libro de texto TE3 (2022), el cual se encuentra actualmente en circulación en el sistema escolar chileno y que, posiblemente se vuelva a reutilizar el 2023, como ha acontecido con los libros de texto que ha estado entregado el MINEDUC estos últimos años al estudiantado del sistema escolar.

Por otro lado, las actividades afines a inferencia estadística formal esencialmente se refieren al cálculo de intervalos de confianza, situación mencionada por Reichardt y Collob (1997) y Batanero (2013), donde se considera una mirada básicamente procedimental, lo que ha denominado Estrella (2017) como una aritmetización de la estadística. Además, el estudiantado debe estudiar numéricamente el efecto del tamaño muestral, el error estándar y el nivel de confianza en la amplitud de los intervalos, sin hacer referencias al uso de herramientas computacionales; tareas que exhortan al estudiantado a analizar la percepción de la variabilidad y al razonamiento de modelos y lenguaje estadístico, acorde al marco del pensamiento estadístico dado por Wild y Pfannkuch (1999) y Garfield y Ben-Zvi (2008).

En este sentido, llama la atención que los libros de texto analizados no hacen referencia explícita al uso de software, como, por ejemplo, Excel o GeoGebra, para realizar simulaciones de manera de tomar decisiones, lo que no está en coherencia a lo mencionado por Wild, Utts y Horton (2018), quienes sostienen que los usuarios de la estadística requieren pensar estadística y computacionalmente. Asimismo, la literatura especializada ha entregado evidencias empíricas acerca de que los y las estudiantes, durante su formación, han adquirido nociones erróneas acerca de conceptos relacionados con los intervalos de confianza (Castro et al., 2007), lo que, eventualmente, incidiría en la interpretación y toma de decisiones, de acuerdo con la fase conclusión (Interpretación y comunicación) del ciclo investigativo de conformidad con el marco sobre pensamiento estadístico de Wild y Pfannkuch (1999).

Por otro lado, las actividades presentadas en los libros de texto analizados no hacen referencia cómo se extrajo la muestra y si ella es producto de un muestreo aleatorio, así como, de la población objeto de estudio, lo cual se encuentra en estrecha relación con la fase Datos (Recolección de datos) del ciclo investigativo. No obstante, con base en el intervalo de confianza se solicita calcular un tamaño muestral dado el error, nivel de confianza y desviación estándar poblacional conocida, tarea donde juega un rol importante el error; es decir, la diferencia en valor absoluto del parámetro con el estimador, aun cuando en los libros de texto no se menciona este concepto. Asimismo, no se introducen ideas acerca de la importancia del muestreo y de los tipos de muestreo en la inferencia estadística.

Igualmente, en relación con la integración de la estadística y el contexto, la redacción de las actividades presentes en los libros de texto analizados da cuenta que, ellas no son extraídas de situaciones reales, esto es, como ha mencionado León (2021), estamos en presencia de una “pseudo-contextualización” (p. 237). Contexto que no permitiría dar sentido a los datos (Coob y Moore, 1997) al momento de las conclusiones e interpretación de la situación problema. Además, los libros de texto analizados no introducen situaciones problemas referidas al ciclo investigativo de Wild y Pfannkuch (1999), donde el estudiantado interactúe con todas sus fases (Problema → Plan → Datos → Análisis → Conclusiones). Es decir, formular un problema, generar un plan de análisis, extraer datos, analizar los datos (Transposición) y obtener conclusiones relacionadas con el problema y preguntas de investigación, así como, evidenciar la importancia de la variabilidad en la estadística, en síntesis, fases del pensamiento estadístico.

Acorde a lo mencionado antes, los autores concuerdan con Batanero (2013) que la forma de presentar los tópicos acerca de inferencia estadística, plantean, en el profesorado de matemática, un desafío didáctico, que, fortuitamente no permitiría una adecuada interpretación de los resultados proporcionados por los intervalos de confianza; debido a que las actividades utilizadas son en principio rutinarias, enfatizando en el uso de fórmulas, sin prestar demasiado interés en la interpretación y la toma de decisiones y el contexto.

Finalmente, el presente estudio proporciona evidencias empíricas sobre como los libros de texto están abordando el concepto de inferencia estadística, aun cuando están en estrecha relación con lo propuesto por distintos investigadores, en particular Batanero (2013) indica que quedan tareas pendientes de abordar por el profesorado en el nivel de sistema escolar y también universitario, como, por ejemplo, la interpretación, la toma de decisiones con base en los resultados dados por un intervalo de confianza y los alcances de las conclusiones. Tareas que pueden ser abordadas en las didácticas específicas, en particular, la relacionada con la estadística y probabilidades, asignatura que poseen los currículos de formación del profesorado de matemática en varias instituciones, en el caso chileno.

Agradecimientos

Este trabajo se ha desarrollado en el marco del proyecto FONDECYT de INICIACIÓN 11220295. Financiado por la Agencia de Nacional de Investigación y Desarrollo de Chile (ANID) y del Proyecto de investigación “Niveles de alfabetización estadística de los profesores en formación: efectividad de la enseñanza”. Código: 2250205 PIDA/R. Financiado por la Dirección de Investigación Universidad del Bio-Bío. Chile.

Conflicto de intereses

Los autores declaran no tener algún conflicto de interés.

Declaración de la contribución de los autores

Los autores afirmamos que se leyó y aprobó la versión final de este artículo. El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: F. R. A. 60 %, M. A. P. 40 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor principal y correspondiente [F. R. A], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://doi.org/10.5281/zenodo.10055561

Referencias

Alvarado, H., Estrella, S., Retamal, L., & Galindo, M. (2018). Intuiciones probabilísticas en estudiantes de ingeniería: implicaciones para la enseñanza de la probabilidad. Revista Latinoamericana de Investigación en Matemática Educativa, 21(2), 131-156. https://doi.org/10.12802/relime.18.2121

Alveal, F. R., & Rubilar, P. R. S. (2012). Habilidades de codificación y descodificación de tablas y gráficos estadísticos: un estudio comparativo en profesores y alumnos de pedagogía en enseñanza básica. Avaliação: Revista Da Avaliação Da Educação Superior (campinas), 17(1). https://doi.org/10.1590/S1414-40772012000100011

Batanero, C. (2005). Significados de la probabilidad en la educación secundaria. Revista Latinoamericana de Investigación en Matemática Educativa, 8(3), 247-264. Recuperado de https://dialnet.unirioja.es/descarga/articulo/2096616.pdf

Batanero, C. (2013). Del análisis de datos a la inferencia: Reflexiones sobre la formación del razonamiento estadístico. Cuadernos, 8(11), 277-291.

Batanero, C., Biehler, R., Engel, J., Maxara, C., & Vogel, M. (2005). Using Simulation to Bridge Teachers Content and Pedagogical Knowledge in Probability. En ICMI-Study 1. Recuperado de http://stwww.weizmann.ac.il/G-math/ICMI/log_in.html

Batanero, C., Díaz, C., Contreras, J., & Roa, R. (2013). El sentido estadístico y su desarrollo. Números. Revista de Didáctica de las Matemáticas, 83, 7-18.

Ben-Zvi, D., & Garfield, J. (2004). Research on Reasoning about Variability: A Forward. Statistical Education Research Journal, 3(2), 4-6. https://doi.org/10.52041/serj.v3i2.536

Ben-Zvi, D., & Makar, K. (2016). The teaching and learning of Statistics. International perspectives. Suiza: Springer International Publishing. https://doi.org/10.1007/978-3-319-23470-0

Borovcnik, M. (2022). The role of probability for understanding statistical inference. ICOTS11 (2022). https://doi.org/10.52041/iase.icots11.T6G1

Castro, A., Vanhoof, S., Noortgate, W., & Onghena, P. (2007). Students’ misconceptions of statistical inference: A review of the empirical evidence from research on statistics education. Educational Research Review, 2(2), 98-113. https://doi.org/10.1016/j.edurev.2007.04.001

Cobb, G., & Moore, D. (1997). Mathematics, Statistics, and Teaching. American Mathematical Monthly, 104(9), 801-823. https://doi.org/10.1080/00029890.1997.11990723

Cobb, T. (2007). Computing the vocabulary demands of L2 reading. Language Learning & Technology, 11(3), 38-63. Recuperado de https://www.lltjournal.org/item/441/

Cobo, B. (2003). Significados de las medidas de posición central para los estudiantes de secundaria (Tesis doctoral). Universidad de Granada, España.

Collins. (2003). Collins English dictionary (6th Revised Edition). Collins.

Curcio, F. R. (1989). Developing graph comprehension. Reston: N. C. T. M.

Engel, J. (2010). On teaching bootstrap confidence intervals. En Reading, C. (Ed.), Proceedings of the eighth International Conference on Teaching Statistics. Voorburg, Países Bajos: International Statistical Institute. Recuperado de http://www.stat.auckland.ac.nz/iase/publications.php (en línea).

Estrella, S. (2017). Enseñar estadística para alfabetizar estadísticamente y desarrollar el razonamiento estadístico. En Salcedo, A. (Ed.), Alternativas Pedagógicas para la Educación Matemática del Siglo XXI (pp. 173-194). Caracas: Centro de Investigaciones Educativas, Escuela de Educación, Universidad Central de Venezuela.

Fidler, F., & Cumming, G. (2005). Interval estimates for statistical communication: Problems and possible solutions [Paper presentation]. IASE Satellite Conference on Communication of Statistics, Sydney, International Association for Statistical Education. https://doi.org/10.52041/SRAP.05201

GAISE. (2005). Guidelines for assessment and instruction in statistics education (GAISE) report: A curriculum framework for PreK-12 statistics education. ASA.

GAISE. (2016). Guidelines for assessment and instruction in statistics education. College report. Alexandria, VA: American Statistical Association. Recuperado de: https://www.amstat.org/asa/files/pdfs/GAISE/GaiseCollege_Full.pdf

Garfield, J., & Ben-Zvi, D. (2008). Developing students’ statistical reasoning: Connecting research and teaching practice. Dordrecht, Países Bajos: Springer.

Giaconi, V., Montenegro, H., Rojas, F., Catalán, M., & Guíñez, F. (2022). Tensiones al enseñar inferencia estadística en la formación inicial docente. Enseñanza de las Ciencias, 40(3), 71-86. https://doi.org/10.5565/rev/ensciencias.5595

Harradine, A., Batanero, C., & Rossman, A. (2011). Students and teachers’ knowledge of sampling and inference. En Batanero, C., Burrill, G., & Reading, C. (Eds.), Teaching statistics in school mathematics. Challenges for teaching and teacher education (pp. 235-246). Nueva Serie ICMI, Springer. https://doi.org/10.1007/978-94-007-1131-0_24

Huerta, M. P. (2020). Hipótesis y conjeturas en el desarrollo del pensamiento del pensamiento estocástico: retos para su enseñanza y en la formación de profesores. Revista Latinoamericana De Investigación En Matemática Educativa, 23(1). https://doi.org/10.12802/relime.20.2313.

León, N. (2021). Enseñanza de la estadística con sentido y en contexto a través de la resolución de problemas. Realidad y Reflexión, 53, 228-253. https://doi.org/10.5377/ryr.v53i53.10897

Makar, K., & Rubin, A. (2009). A framework for thinking about informal statistical inference. Statistics Education Research Journal, 8(1), 82-105. https://doi.org/10.52041/serj.v8i1.457

Mayring, P. (2000). Qualitative Content Analysis. Forum Qualitative Sozialforschung/ Forum: Qualitative Social Research, 1(2). https://doi.org/10.17169/fqs-1.2.1089

McMillan, J., & Schumacher, S. (2011). Investigación educativa. Pearson-Adisson Wesley.

Meletiou-Mavrotheris, M., Lee, C., & Fouladi, R. (2007). Introductory statistics, college student attitudes and knowledge-a qualitative analysis of the impact of technology-based instruction. International Journal of Mathematical Education in Science and Technology, 38(1), 65-83. https://doi.org/10.1080/00207390601002765

MINEDUC-CPEIP. (2020). Informe Resultados Nacionales. Evaluación Nacional Diagnóstica de la Formación Inicial Docente 2019. Centro de Perfeccionamiento, Experimentación e Investigaciones Pedagógicas.

Moore, D. S. (2004). The basic practice of statistics (3rd ed.). Nueva York: W. H. Freeman.

Pfannkuch, M. (2006). Informal inferential reasoning. En Rossman, A., & Chance, B. (Eds.), Proceedings of the Seventh International Conference on Teaching Statistics [CD]. Voorburg, Países Bajos: International Association for Statistics Education.

Pfannkuch, M., Wild, C. J., & Parsonage, R. A. (2012). Conceptual pathway to confidence intervals. ZDM Mathematics Education, 44, 899-911. https://doi.org/10.1007/s11858-012-0446-6

Reaburn, R. (2014). Students’ understanding of confidence intervals. En Makar, K., B. de Sousa, & Gould, R. (Eds.), Proceedings of the Ninth International Conference on Teaching Statistics. Voorburg, Países Bajos: IASE.

Reading, C., & Shaughnessy, M. (2004). Reason about variation. En Ben-Zvi, D., & Garfield, J. (Eds.), The Challenge of Developing Statistical Literacy, Reasoning, and Thinking (pp. 201-226). Países Bajos: Kluwer Academic Publishers. https://doi.org/10.1007/1-4020-2278-6_9

Reichardt, C. S., & Gollob, H. F. (1997). When confidence intervals should be used instead of statistical tests, and vice versa. En Harlow, L. L., Mulaik, S. A., & Steiger, J. H. (Eds.), What if there were no significance tests? (pp. 259-284). Londres: Lawrence Erlbaum Associates, Publishers.

Rodríguez-Alveal, F., & Maldonado-Fuentes, A. (2023). Tipología de las preguntas acerca del concepto variabilidad en los textos escolares y su relación con la Alfabetización y pensamiento estadístico. Uniciencia, 37(1), 65-83. https://doi.org/10.15359/ru.37-1.4

Rossman, A. (2008). Reasoning about informal statistical inference: One statistician’s view. Statistics Education Research Journal, 7(2), 5-19. https://doi.org/10.52041/serj.v7i2.467

Ruz, F., Chance, B., Medina, E., & Contreras, J. M. (2021). Content knowledge and attitudes towards stochastics and its teaching in pre-service Chilean mathematics teachers. Statistics Education Research Journal. https://doi.org/10.52041/serj.v20i1.100

Sabbag, A., Garfield, J., & Zieffler, A. (2018). Assessing statistical literacy and statistical reasoning: The reali instrument. Statistics Education Research Journal, 17(2), 141-160. Recuperado de https://doi.org/10.52041/serj.v17i2.163

Shi, H., & Yin, G. (2021). Reconnecting p-Value and Posterior Probability Under One- and Two-Sided Tests. The American Statistician, 75(3), 265-275. https://doi.org/10.1080/00031305.2020.1717621

Watson, J., Fitzallen, N., Fielding-Wells, J., & Madden, S. (2018). The Practice of Statistics. En Ben-Zvi, D., Makar, K., & Garfield, J. (Eds.), International Handbook of Research in Statistics Education. Springer International Handbooks of Education. Cham: Springer. https://doi.org/10.1007/978-3-319-66195-7_4

Wild, C. y Pfannkuch, M. (1999). Statistical thinking in empirical enquiry. International Statistical Review, 67(3), 223-265. https://doi.org/10.2307/1403699

Wild, C. J., Utts, J. M., & Horton, N. J. (2018). What is statistics? In Ben-Zvi, D., Makar, K. & Garfiel, J. (Eds.), International Handbook of Research in Statistics Education (pp. 5-36). Gewerbestrasse: Springer. https://doi.org/10.1007/978-3-319-66195-7_1

---

1. 1* Autor para correspondencia

   Francisco Rodríguez-Alveal, frodriguez@ubiobio.cl, http://orcid.org/0000-0003-2169-0541

   Maitere Aguerrea, maguerrea@ucm.cl, https://orcid.org/0000-0002-7513-982X

   Departamento Ciencias de la Educación, Facultad de Educación y Humanidades, Universidad del Bío-Bío, Chillán, Chile.

1. 2 Departamento de Matemática, Física y Estadística, Facultad de Ciencias Básicas, Universidad Católica del Maule, Talca, Chile.