Niveles de razonamiento proporcional y micromundos. Un estudio en telesecundaria unitaria

Levels of proportional reasoning and microworlds. A study on unitary tele-secondary education

Níveis de raciocínio proporcional e micromundos. Um estudo em escolas unitárias de ensino médio à distância

Carlos Alberto Lugo Lugo1, Erika García Torres1*, Santiago Alonso Palmas Pérez2

Received: Sep/15/2023 • Accepted: Jan/26/2024 • Published: Jul/31/2024

Resumen [Objetivo] El razonamiento proporcional es un tipo de corriente compleja que implica reconocer comparaciones como la covariación entre magnitudes y comparaciones múltiples. El objetivo de este estudio fue analizar el razonamiento proporcional de alumnos de telesecundaria unitaria utilizando los niveles propuestos por Karplus (1983) a partir de un micromundo como GeoGebra. En el micromundo, el estudiantado puede explorar y construir significados sobre los objetos matemáticos. [Metodología] Se diseñaron cuatro actividades en GeoGebra, las cuales fueron aplicadas a 18 estudiantes de una telesecundaria unitaria (modalidad educativa en México). [Resultados] Se identificó que los participantes están en niveles iniciales, que responden a estructuras aditivas, cualitativas o erróneas para justificar sus procedimientos. Los niveles más complejos de razonamiento proporcional relacionados con el uso de razones y constantes de proporcionalidad se obtuvieron cuando el estudiantado interactuaba con sus pares y con el micromundo. Los niveles de razonamiento no son mutuamente excluyentes, debido a que el alumnado puede razonar de diferente manera según la situación y las posibilidades del software. [Conclusiones] El uso de micromundos en la exploración del razonamiento proporcional posibilita acciones que no pueden llevarse a cabo en “lápiz y papel”, lo cual brinda la oportunidad de interactuar con construcciones en movimiento, además genera interacciones de reforzamiento o construcción de saberes desarrollados en conjunto. Palabras clave: educación; matemática escolar; razonamiento proporcional; micromundo; telesecundaria unitaria. Abstract [Objective] Proportional reasoning is a type of complex thinking that involves recognizing comparisons such as the covariation between magnitudes and multiple comparisons. The aim of this study was to analyze proportional reasoning of students from unitary tele-secondary education using the levels proposed by Karplus (1983) through a microworld like GeoGebra. In the microworld, students can explore and construct meanings about mathematical objects. [Methodology] Four activities were designed in GeoGebra, which were administered to 18 students from a unitary tele-secondary school, an educational modality in Mexico. [Results] It was found that participants are at initial levels that correspond to additive, qualitative, or erroneous structures to justify their procedures. The more complex levels of proportional reasoning, related to the use of ratios and constants of proportionality, were achieved when students interacted with each other and with the microworld. The reasoning levels are not mutually exclusive, as students can reason differently depending on the situation and the software’s capabilities. [Conclusions] The use of microworlds in exploring proportional reasoning enables actions that cannot be carried out with pencil and paper, providing opportunities to interact with moving constructions. Additionally, it fosters interactions that reinforce or build collective knowledge. Keywords: Education; school mathematics proportional reasoning; microworld; unitary tele-secondary education. Resumo [Objetivo] O raciocínio proporcional é um tipo de fluxo complexo que envolve o reconhecimento de comparações, como a covariação entre magnitudes e comparações múltiplas. O objetivo deste estudo foi analisar o raciocínio proporcional de alunos de escolas unitárias do ensino médio à distância usando os níveis propostos por Karplus (1983) a partir de um micromundo como o GeoGebra. No micromundo, os alunos podem explorar e construir significados sobre objetos matemáticos. [Metodologia] Quatro atividades do GeoGebra foram elaboradas e aplicadas a 18 alunos em uma escola unitária do ensino médio à distância (modalidade educacional no México). [Resultados] Identificou-se que os participantes estão em níveis iniciais, respondendo a estruturas aditivas, qualitativas ou errôneas para justificar seus procedimentos. Os níveis mais complexos de raciocínio proporcional relacionados ao uso de razões e constantes de proporcionalidade foram obtidos quando os alunos interagiram com seus colegas e com o micromundo. Os níveis de raciocínio não são mutuamente exclusivos, pois os alunos podem raciocinar de forma diferente, dependendo da situação e das possibilidades do software. [Conclusões] O uso de micromundos na exploração do raciocínio proporcional possibilita ações que não podem ser realizadas com “lápis e papel”, o que oferece a oportunidade de interagir com construções em movimento e também gera interações de reforço ou construção de saberes desenvolvidos em conjunto. Palavras-chave: educação; matemática escolar; raciocínio proporcional; micromundo; escola unitária de ensino médio à distância.

Introducción

El razonamiento proporcional (en adelante RP) es una de las nociones matemáticas que se trabajan en diferentes niveles educativos y a través de una variedad de acercamientos. Es un tipo de pensamiento complejo que implica reconocer comparaciones como la covariación entre magnitudes y comparaciones múltiples; además, se relaciona con los métodos del pensamiento cualitativo y cuantitativo (Heller et al., 1989).

Este tipo de razonamiento no solo está presente en las matemáticas, sino que es fundamental en la estructura descriptiva de la física y otras ciencias (Mochón, 2012), por lo que Piaget lo consideraba como un componente básico del razonamiento formal, el cual es necesario para adquirir conceptos como el de probabilidad y correlación (Godino y Batanero, 2003). Existen diferentes aproximaciones y formas de razonar correspondientes al razonamiento proporcional, aunque algunas de ellas resultan erróneas, como es el caso de las relaciones aditivas o de la “regla de tres” cuando es aplicada de manera mecánica y en situaciones no proporcionales. Algunos estudios han identificado que el alumnado de secundaria atiende las situaciones proporcionales desde estas estrategias (Sánchez, 2013), de tal forma que el razonamiento proporcional no se comprende desde sus diferentes aplicaciones.

Dentro del sistema educativo de México, el RP se incluye en los planes y programas de la educación secundaria. Sin embargo, la construcción del RP se construye a lo largo de la etapa de educación básica, comenzando con nociones aditivas y algunas situaciones multiplicativas en primaria baja (de 6 a 8 años); después, continúa en primaria alta (de 9 a 12 años) al introducir términos como noción o problemas de valor faltante, y luego pasar a la educación secundaria (de 12 a 15 años) en donde se aborda la proporcionalidad directa, inversa y la combinación de ambas (SEP, 2017).

En la educación secundaria se busca formalizar el RP a partir de las herramientas del álgebra como funciones lineales, con énfasis en obtener su expresión algebraica y graficación, así como en el análisis de sus características estructurales (Butto et al., 2019). De forma que, en el paso de la educación primaria a la secundaria existe un cambio en las situaciones propuestas con respecto al RP, así como el lenguaje que se emplea, pues en educación primaria se utiliza un lenguaje aritmético, mientras que en secundaria se introduce el algebraico.

En particular, este estudio se centra en la atención de la telesecundaria unitaria, pues es una de las modalidades que no cuenta con una propuesta curricular específica para sus características de organización multigrado (varios grados escolares en un mismo grupo) (García, Santiago y Zepeda, 2019); pero esto tiene ventajas pedagógicas. Entre las posibilidades de una escuela de organización multigrado se tiene la construcción del aprendizaje en colectivo ante la diversidad de edades, formas de pensar y razonamientos (Bustos, 2013). Estas construcciones del estudiantado involucran una discusión y toma de decisiones, lo cual favorece su comunicación matemática y la justificación de sus resultados.

A partir del uso de un micromundo seleccionado (GeoGebra) y una serie de actividades desarrolladas en él, se busca identificar cómo el alumnado de telesecundaria unitaria (tres grados escolares en un mismo grupo) se aproxima al RP, al identificar el tipo de razonamiento a partir de una clasificación por niveles (Karplus et al., 1983), teniendo como principal enfoque las interacciones entre estudiantes multigrado, estudiante-micromundo y micromundo-RP.

Marco teórico

Razonamiento proporcional

El RP es un razonamiento matemático (Fernández y Llinares, 2012) que denota un sistema de dos variables entre las que existe una relación de función lineal y puede caracterizarse como multiplicativa constante (Karplus et al., 1983). Se refiere a detectar, analizar, explicar y proporcionar evidencia en apoyo de afirmaciones sobre relaciones proporcionales (Lamon, 2020); además, no solo implica el entendimiento de la relación multiplicativa entre dos cantidades, sino que también implica la habilidad para discriminar situaciones proporcionales de las que no lo son (Modestou y Gagatsis, 2010).

La proporcionalidad comienza a construirse en los primeros años educativos de manera cualitativa y lógica, antes de que se estructure cuantitativamente (Butto et al., 2019), lo cual permite llegar a comprender situaciones proporcionales bajo términos del tipo “en ambos casos crecen” o “las dos disminuyen”.

Con respecto al RP en secundaria, se ha detectado que el estudiantado de este nivel acude con mayor comodidad al análisis cualitativo que al cuantitativo, y cuando se aproximan de forma cuantitativa, utilizan principalmente el análisis de índole aditivo (Sánchez, 2013), lo cual es una aproximación errónea.

Existen cuantiosos estudios enfocados en el RP, de los cuales se han identificado como pioneros los trabajos de Karplus 1983 y Lesh (1988). En este estudio se retoma una categorización de niveles de razonamiento proporcional propuesta por Karplus 1983 y obtenida a partir de las respuestas de estudiantes de distintos grados al problema “Mr. Tall/Mr. Short” (Figura 1). Este problema, sobre la relación proporcional entre alturas de dos personas Mr. Tall y Mr. Short, propició diversos argumentos para su resolución, los cuales permitieron identificar similitudes entre las personas participantes, por lo que se construyeron teóricamente los niveles de razonamiento (Tabla 1).

Figura 1. Problema “Mr. Tall/ Mr. Short”, tomado de Lamon (2020).

Tabla 1. Niveles de razonamiento proporcional

Niveles de razonamiento proporcional
Nivel	Descripción
Incompleto	Se adivina la respuesta o se emplea una operación cuantitativa inapropiada. Se es capaz de identificar la relación entre dos magnitudes, pero en el intento de resolver, se emplea alguna operación que no lleva a una solución adecuada, ya sea porque la operación no es la correcta o porque el algoritmo fue mal desarrollado.
Cualitativo	Se comparan las cuatro cantidades dadas usando los términos más, menos o términos equivalente. El razonamiento proporcional aparece en etapas iniciales bajo un razonamiento cualitativo, por lo que se puede identificar una situación de proporcionalidad cuando esta aumenta o disminuye, pero aún no logra emplear un proceso cuantitativo.
Aditivo	Estrategia incorrecta que hace uso de diferencias en parte o todo el razonamiento en vez de una relación multiplicativa. Este nivel se desarrolla desde un razonamiento cuantitativo, pero vincula los datos bajo estructuras aditivas.
Preproporcional	Uso de factores multiplicativos para relacionar cantidades. Se reconoce la situación de proporcionalidad, y se identifica el uso de los factores multiplicativos; esta categoría está muy cercana al razonamiento proporcional, pero aún no se logra establecer la igualdad de razones, el razonamiento parte del reconocimiento del valor unitario.
Proporcional	Uso directo de razones y su equivalencia o no. Dentro del desarrollo del razonamiento proporcional, esta categoría es donde se puede asumir que ya se ha desarrollado un razonamiento completo, pues logra identificar las situaciones proporcionales de las que no la son, se identifican términos como razón y constante de proporcionalidad, además si los procedimientos son correctos.

Nota: propuesta tomada de Karplus (1983).

A partir de esta categorización se busca comprender el nivel de RP que tiene el alumnado de telesecundaria unitaria en el uso de los recursos tecnológicos bajo la conceptualización y la perspectiva teórica de los micromundos.

Micromundos

Un micromundo se define como un ambiente computacional para la incorporación de un conjunto coherente de conocimientos científicos y de relaciones diseñadas, de forma que, con un conjunto adecuado de tareas y con principios pedagógicos, un grupo de estudiantes puede participar en la exploración y construcción de actividades ricas en generación de significados (Healy y Kynigos, 2010).

La intención de involucrarse con un micromundo es orientar al estudiantado hacia maneras matemáticas de pensar a través de estructuras establecidas por el diseñador y el software, los alumnos deben mantener cierta autonomía, así como asumir la responsabilidad de sus acciones y de los resultados obtenidos (Noss y Hoyles, 2019). A pesar de que el trabajo no tiene fines didácticos, el diseño creado puede ayudar a desarrollar dichas habilidades en el alumnado.

De manera específica, un micromundo matemático es un lugar para familiarizarse con un conjunto de ideas, de situaciones problemáticas o de actividades, en donde estudiante y docente pueden probar opiniones sobre un tema de interés; además, la meta es la construcción de significado y de relaciones que sirvan como modelo para un sistema formal, dando oportunidades para crear modelos mentales capaces de reflejar la estructura y composición de los sistemas formales (Weir, 1987); es decir, a través de la manipulación de los micromundos, el alumnado es capaz de probar hipótesis o procedimientos que lo lleven a una formalización del aprendizaje.

Para que un ambiente computacional se considere un micromundo debe tener cuatro componentes (Hoyles y Noss, 1987) (Figura 2):

• El componente del estudiante. Entendimientos y concepciones parciales existentes que cada estudiante trae consigo a la situación didáctica.

• El componente técnico. Es considerado el componente central. Software o lenguaje de programación y un conjunto de herramientas que proveen un sistema de representaciones para comprender una estructura matemática o campo conceptual.

• El componente pedagógico. Estructura de la investigación y exploración de los conceptos plasmados en el componente técnico (los aspectos físicos pueden ser docente, libro, cartel, entre otros).

• El componente contextual. Entorno social de las actividades.

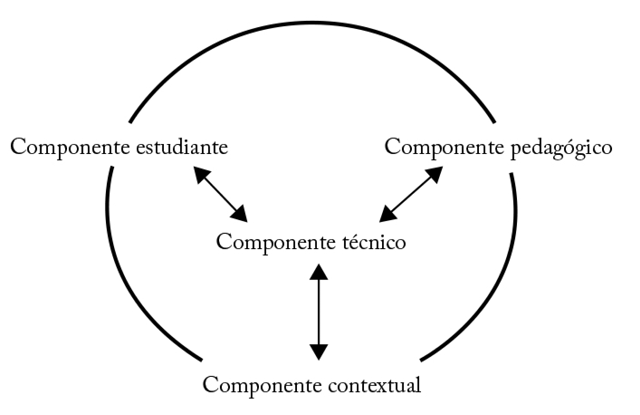
Figura 2. Relación de componentes que integran un micromundo

Nota: modelo basado en la propuesta de Hoyles y Noss (1987).

Telesecundaria unitaria

Situando el componente contextual, el nivel educativo considerado como idóneo para analizar el RP a partir de la interacción con un micromundo es la secundaria. Lo anterior porque en este nivel se formalizan las nociones que se han trabajado en etapas anteriores (educación primaria), tales como porcentajes y conversión de magnitudes. En secundaria surgen términos relacionados a la proporcionalidad directa e inversa, constante, razón, entre otros.

Dentro de las modalidades presentes en secundaria, se ubica la telesecundaria, la cual es atendida con apoyo de una persona docente por grupo (SEP, 2017), quien ofrece un servicio educativo con el apoyo de los medios electrónicos de comunicación social y con materiales impresos (Flores y Albarrán, 2008).

En la telesecundaria tiene presencia la organización escolar multigrado, en la que el personal docente atiende a estudiantes de diversos grados en una misma aula. Estas escuelas surgen ante la necesidad de atender alumnos y alumnas que viven en zonas donde no ha sido posible establecer una secundaria general o técnica por diferentes condiciones (distancia, contexto rural, número de población, entre otros).

En el país, estas escuelas representan el 33.1 % en telesecundarias, secundarias comunitarias e indígenas (de 12 a 15 años), y atienden al 9.7 %, 8.6 % y 10.2 % de estudiantes, respectivamente (Mejoredu, 2022). Si bien no es un porcentaje mayor a la mitad de las telesecundarias, el realizar estudios en esta modalidad ayuda a visualizar la educación desde un panorama alejado del currículo segmentado por grados escolares, lo cual permite visualizar qué sucede en una aula donde predomina la diversidad, identificando la combinación de experiencias, conocimientos, actitudes y formas de pensar, lo cual puede suscitar un aprendizaje colectivo y desarrollar su capacidad de argumentación y discusión entre pares (Bustos, 2013).

En la educación multigrado, las interacciones determinan una relación con los demás elementos que influyen en la construcción colectiva de conocimiento, pues el espacio es atravesado por tensiones, cambios y contradicciones abiertas a múltiples flujos culturales, locales y globales (Corro y Bolaños, 2018). Una interacción es entendida como la comunicación entre los pares, y es mediante este proceso que los sujetos adquieren la capacidad reflexiva para verse a sí mismos, así como dar forma y sentido a la realidad que los rodea (Rizo, 2006).

Por tanto, el ubicar a las interacciones como un medio para analizar el RP favorece a la compresión de la toma de decisiones, los intercambios de experiencias y saberes, las negociaciones y los resultados a los que llegaron las personas participantes en cada actividad. Es importante mencionar que las interacciones hacen referencia a los intercambios entre quienes participaron, así como las interacciones en el micromundo.

Objetivo

A partir de la descripción del RP, de micromundos y de telesecundaria unitaria, este estudio tiene como objetivo explorar niveles de razonamiento proporcional en alumnos de telesecundaria unitaria a través del uso de micromundos. Para cumplir con el objetivo se ha diseñado una serie de actividades que permiten observar y comprender los argumentos y el porqué de las respuestas del alumnado.

Metodología

El estudio es cualitativo con alcance exploratorio y la población estuvo integrada por 18 participantes, pertenecientes a una telesecundaria unitaria en el Estado de Guanajuato, México, ubicada en un contexto rural. De las 18 personas participantes, cinco pertenecen a primer grado (12-13 años), ocho a segundo (13-14 años) y cinco a tercer año (14-15 años). Para su participación se solicitó el consentimiento informado de sus padres, madres o tutores legales y su asentimiento antes del desarrollo de las actividades.

Dentro de los diferentes softwares educativos que existen, se consideró a GeoGebra para el desarrollo del micromundo porque su manipulación permite crear situaciones en donde los sujetos pueden probar hipótesis o procedimientos, al identificar elementos desde diferentes áreas matemáticas, inclusive, las herramientas con las cuales cuenta permite ver modelos en movimiento y analizar diferentes versiones de una sola representación (Barros y Stivam, 2012). A partir de estas consideraciones se desarrollaron cinco actividades.

Actividad 1. Exploración

La primera actividad fue de exploración libre (Figura 3), se consideró necesario incluir un espacio en donde conocieran las herramientas, su funcionamiento y las acciones a ejecutar de acuerdo con la calculadora geométrica.

Figura 3. Actividad 1. Exploración

Actividad 2. Relación entre segmentos por un deslizador

Una de las herramientas básicas utilizadas de GeoGebra fue el deslizador, debido a que ayuda a explorar una relación en movimiento constante. Por medio de la manipulación del deslizador un segmento crece con los mismos valores, mientras que otro lo hace en una relación de 3:1 (Figura 4). El objetivo era que el estudiantado identificara qué tipo de relación existe entre los segmentos y qué papel juega el deslizador en términos matemáticos.

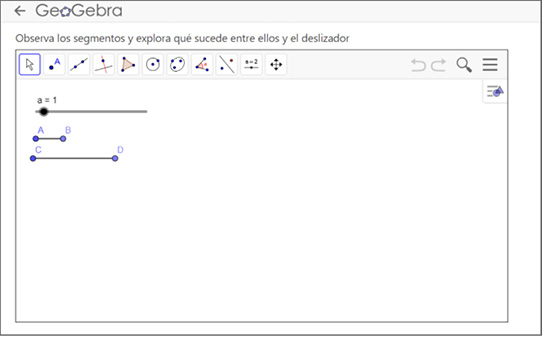
Figura 4. Actividad 2. Relación entre segmentos por un deslizador

Actividad 3. Construcción de dos segmentos bajo una razón dada

El diseño de esta actividad es continuación de la actividad dos, debido a que después de identificar la relación entre los segmentos según el deslizador (independientemente del nivel reflejado), se consideró que en esta actividad los alumnos y las alumnas pudieran establecer la relación creando un deslizador de acuerdo con la razón de 0.5:1 (Figura 5), explorando la función del deslizador en términos matemáticos, siendo el nivel proporcional donde pudieran reconocer la constante de proporcionalidad.

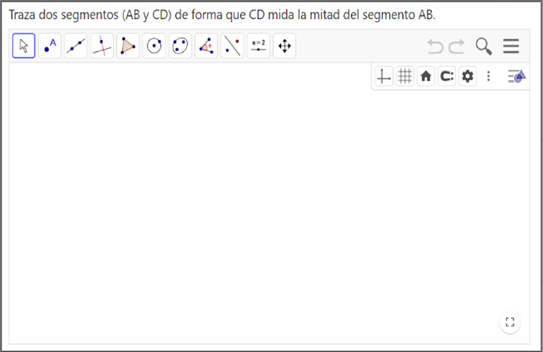
Figura 5. Actividad 3. Construcción de dos segmentos bajo una razón dada

Actividad 4. Relación entre triángulos semejantes

La actividad presenta la relación entre las longitudes de los lados de los triángulos rectángulos, los cuales estaban diseñados en una relación de semejanza de 2:1; como primera parte de la actividad se exploró la relación entre los triángulos (Figura 6). Una característica de los triángulos es que a pesar de encontrarse en una relación de semejanza, su área no cumple dicha relación, por lo cual, como segunda parte de esta actividad, se debía buscar la forma de que su área presentara una relación de 2:1, al hacerlo debían describir qué sucedía con sus lados.

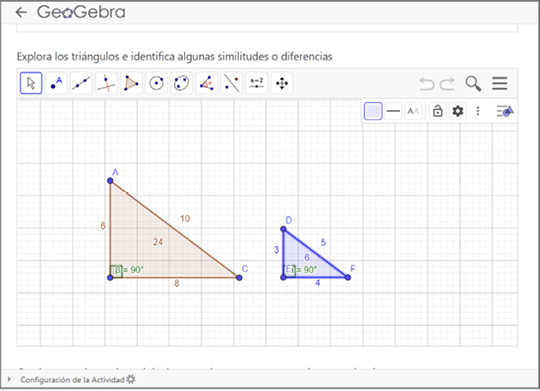
Figura 6. Actividad 4. Relación entre triángulos semejantes

Actividad 5. Construcción de un mosaico con un factor escala

Como actividad final, se planteó la construcción de un mosaico con un factor escala de 1.5:1, de acuerdo con una construcción original, en donde, a diferencia de las actividades anteriores, la razón no está dada en números enteros o de forma evidente, pues quienes participaron debían explorar cuál es la razón a partir de dos medidas otorgadas, en donde la única condición es que, al final, el mosaico que se construya debe guardar semejanza con el original, pero con las nuevas medidas calculadas (Figura 7).

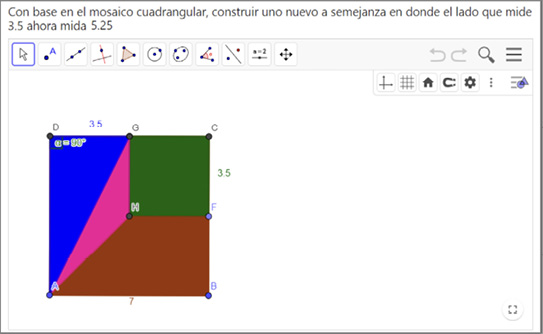
Figura 7. Actividad 5. Construcción de un mosaico con un factor escala

Para la aplicación de las actividades, el estudiantado se organizó en cuatro equipos de trabajo en los que se respetó la modalidad unitaria; es decir, había estudiantes de diferentes grados escolares en un mismo equipo, además se contó con la participación de una persona observadora, quien registraba los datos en audio y video. Su función principal fue documentar aquellos elementos observables y audibles referentes a las actividades en términos de RP, relación entre pares y relación con el micromundo; esto, por las condiciones del salón de clase, no podía ser capturado con los dispositivos de registro.

La intención central de las actividades era permitir una exploración libre, además de que las intervenciones de la persona investigadora tenían la función de provocar la interacción entre pares, para que, a su vez, el alumnado integrara los diferentes componentes del micromundo y expusieran y debatieran sus conocimientos sobre el RP.

Análisis y resultados

Como se ha mencionado, el objetivo fue caracterizar el RP del estudiantado de telesecundaria unitaria a partir de la integración de un micromundo; para ello fue necesario consolidar una unidad de análisis y las categorías observables a partir del tratamiento de los datos. La unidad de análisis se conformó con las interacciones entre las personas participantes con el micromundo, las cuales tienen ciertas características dependiendo de los integrantes y su forma de interactuar en el grupo.

Una interacción es entendida como la comunicación con otra persona distinta, y es mediante este proceso que los sujetos adquieren la capacidad reflexiva para verse a sí mismos y mismas, así como para dar forma y sentido a la realidad que les rodea (Rizo, 2006). Con esto se pretende evidenciar el RP de las personas participantes de acuerdo con su participación, tanto al interior de los equipos como en todo el grupo unitario.

Las categorías de análisis se centraron en tres elementos esenciales: los niveles de RP, los componentes de un micromundo y las interacciones entre el estudiantado participante (Figura 8). Se diferencian las interacciones por quiénes interactúan (actores) y por su intencionalidad (tipo). Entre las primeras se establecieron interacciones entre estudiantes, entre la persona investigadora (aplicadora) con el alumnado, el grupo y los equipos de trabajo. En relación con el tipo, se distinguieron por la intencionalidad de quien interactuaba (ayudas, tutoría y negociación) y por el componente técnico (exploratoria, consecuencial, resolutiva).

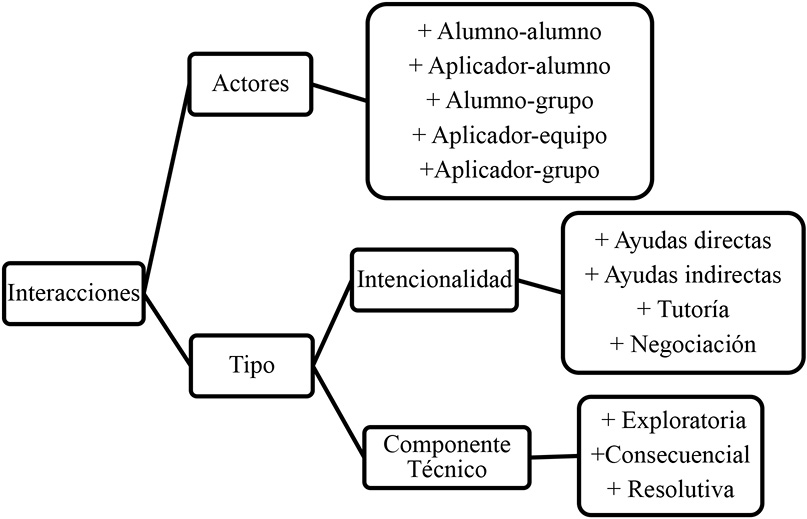
Figura 8. Clasificación de interacciones

Nota: fuente propia de la investigación.

Con base en la caracterización de Block et al. (2015) sobre las ayudas en un aula multigrado, en este estudio se identificaron las ayudas directas como aquellas en donde interactúan la persona aplicadora-estudiante, con el propósito de responder preguntas del alumnado en relación con el RP o a alguna herramienta del micromundo. Se identificaron ayudas indirectas entre quien aplica y el estudiantado, en las cuales las intervenciones que realizaba la persona aplicadora favorecían la integración del alumnado con el micromundo; esto potencializó sus respuestas y los intercambios de ideas, experiencias y conocimientos al interior de los equipos de trabajo, así como la capacidad para externar sus acuerdos con el grupo.

Las intervenciones de tutoría (Corro y Bolaños, 2018) establecen una relación entre pares donde una persona funge como tutora (quien cuenta con mayor experiencia o conocimiento respecto a una tarea) y la otra como tutorada (con menor experiencia o conocimiento en una tarea). En este caso se identificaron las intervenciones entre pares que tienen como intención orientar, sugerir o guiar la actividad, llamando tutor(a) a quien tiene las intenciones mencionadas y tutorado(a) a quien lleva a cabo las orientaciones que recibe por parte de la persona tutora.

En cuanto a la negociación, corresponde a interacciones en las que se establece un diálogo orientado a la negociación de conceptos o ideas vinculadas con el micromundo y sus componentes. Se identificó que en estas interacciones ninguna de las personas participantes tomaba el papel de tutora o de tutorada, sino que exponían en igualdad de condiciones sus opiniones, lo cual evidenciaba al RP.

Dentro de las interacciones del componente técnico se han identificado tres: exploratorias, consecuenciales y resolutivas, cada una implica una función específica en el micromundo, una actividad matemática y un tipo de opiniones, ideas o argumentos construidos en colectivo. Son interacciones que se dan en función del uso del micromundo, aquellas que solo pueden surgir a partir del ambiente que propone el micromundo y las relaciones entre sus componentes.

Se considera una interacción de exploración a los primeros acercamientos para atender a la actividad, y se identifican en su diálogo ideas como “y si”, “deja ver”, “mueve el de allá”, las cuales reflejan un posible procedimiento que consideran aplicable, y la manera de comprobarlo es interactuando con el micromundo. Las interacciones consecuenciales se refieren a las acciones, acuerdos e ideas que después de llevarlas a cabo tuvieron como consecuencia una construcción, el manejo de alguna herramienta o la comprobación de un procedimiento o su descarte.

Finalmente, las interacciones resolutivas son aquellas que favorecieron a la resolución de la actividad; pueden constituir todo un desarrollo o solo una acción determinante que tuvo como consecuencia un resultado o una reflexión sobre las actividades diseñadas.

A continuación se presentan algunos de los resultados en términos de los niveles de RP, la relación entre niveles y evolución de niveles, considerando ambas categorías como el aporte más relevante del estudio, pues como parte de los antecedentes y referentes teóricos no se encontraron indicios al respecto.

Relación entre niveles

Se identificó que los niveles no son mutuamente excluyentes en todos los casos, sino que hay razonamientos propios de cada nivel, pero que se integran en torno a un mismo argumento o procedimiento realizado por las personas participantes; si bien, en el referente teórico de los niveles de RP no se expresa una relación de este tipo, se considera pertinente agregar esta categoría; sobre todo porque el análisis no es individual (por participante) sino colectivo. Ante esto, determinar que todo el estudiantado se encuentra en un mismo nivel a partir de una situación restaría importancia a algunas construcciones en colectivo, sobre todo, si se considera que pertenecen a una telesecundaria unitaria.

La relación entre niveles se referirá a la integración de diferentes razonamientos en torno a una misma situación. Las relaciones identificadas fueron: incompleto-aditivo, cualitativo-aditivo-preproporcional, incompleto-preproporcional y preproporcional-proporcional.

Relación incompleto-aditivo

En las relaciones establecidas entre niveles, se han identificado diferentes causas independientemente de cuáles niveles estén relacionados; por ejemplo, a continuación (figuras 9 y 10) se muestra una interacción correspondiente a la actividad cinco (construcción de un mosaico a partir de otro bajo una razón de 1.25:1), la cual evidencia la relación de razonamientos a partir de la justificación de un procedimiento incorrecto:

E-2.2: A ver saca la medida de todo esto para saber de cuánto tiene que quedar.

E-2.1: 3.5 más 3.5 son 7.

E-2.2: No, pero es que 7 por tres son…

E-2.1: 3.5 más 3.5… 7, 14, 7 más 7 es 14 más otros 7, 21 más otros 7, 28.

E-2.2: Cuál 28.

E-2.1: Entonces nos tiene que salir de 28/refiriéndose al contorno del mosaico/si este salió de 3 cuadros y medio este va a ser de 4.

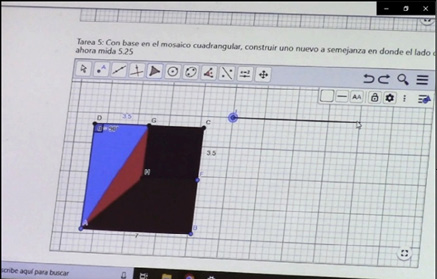
Figura 9. Actividad 5. Trazo de un lado del cuadrado basado en la cuadrícula de apoyo (relación entre incompleto y aditivo)

E-2.1: Cuánto salió para bajo 4, entonces de 4 cuadros y medio.

E-2.2: Tiene que salir de 7 y de 17.50.

E-2.1: ¿Por qué 17? Si está estos lados, más estos lados, más estos lados.

E-2.2: No, pero ahora ya va a ser este, 5.25 más este 7, 17.50, tiene que darte eso 17.50.

E-2.1: Se pasa de 17.50.

E-2.2: Y con mucho.

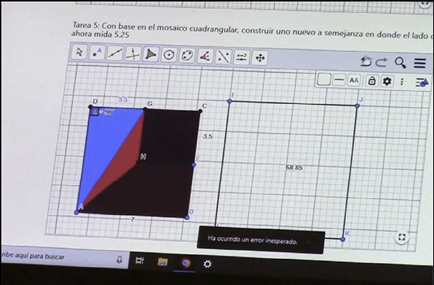
Figura 10. Actividad 5. Confusión del contorno (perímetro) con el área del cuadro trazado (relación incompleto aditivo)

La interacción es estudiante-estudiante, a partir de una negociación donde se pretendía encontrar las medidas del nuevo mosaico. El componente técnico puede clasificarse como una interacción exploratoria, pues al tratar la información (longitud de los lados) no llegan a establecer alguna consecuencia o una solución, más bien comprenden que la hipótesis planteada no resuelve la situación.

Respecto al RP, se reconocen dos razonamientos de diferente nivel, por un lado, el incompleto y, por el otro, el aditivo. Al comienzo de la interacción, la persona participante E-2.1 explicita un razonamiento aditivo en el intento de saber cuánto debe ser el contorno del mosaico, se basa en que la medida de referencia es 3.5 y decide sumarlo dos veces, con lo cual obtiene como resultado 7, por lo que continúa con su estrategia aditiva sumando 7 tres veces más, pues conoce que el mosaico es cuadrangular.

A partir de esta estrategia, determinan que el mosaico debe tener un contorno de 28, pero ante este resultado interviene un razonamiento incompleto, pues confunden la magnitud a la que hacen referencia; es decir, el 28 tiene referencia con las unidades en las cuales se expresan las medidas, mientras que al decir “si este salió de 3 cuadros y medio este va a ser de 4” hace referencia a la cuadrícula del fondo.

Ante la propuesta del alumno E-2.1, interviene la alumna E-2.2, y de esa interacción se sugiere que “tiene que salir de 7 y de 17.50”, para después agregar “ora 5.25 más este 7, 17.50, tiene que darte eso 17.50”. Se identifica un razonamiento aditivo, pues recurre a la suma de medidas para sugerir una medida final del contorno, resultando interesante la mención de “5.25 más 7 es 17.50”, por lo cual se puede suponer que en realidad suma dos veces 5.25, esto correspondería a la medida de un lado del nuevo mosaico, sumando 7 más, la medida del mosaico original.

Como cierre de la interacción, se aprecia de nuevo un razonamiento incompleto, pues las medidas obtenidas representaban el contorno de los mosaicos, pero como se aprecia en la Figura 9 cambian la magnitud de longitud por una de área, especificando que el área del cuadrado que acaban de trazar tiene un valor muy elevando por encima de 17.50, el resultado esperable.

Se identifica que la interacción entre niveles se da a partir de la justificación de un procedimiento erróneo, por lo cual se puede concluir que el estudiantado está consciente de que hay una relación cuantitativa, pero en la búsqueda de una posible solución el razonamiento es incorrecto.

Relación incompleto-preproporcional

Ahora bien, se muestra una interacción correspondiente a la actividad dos (relación de dos segmentos bajo una razón de 3:1), la cual evidencia la relación de razonamientos a partir una corrección:

E-4.1: Ocho veces más no, ¿ocho por cuánto te da 24?

E-4.4: Ocho por tres.

E-4.1: No… Sí, ocho por tres es 24.

E-4.3: Son tres, tres veces.

La interacción se da a lo interno del equipo cuatro a partir del cuestionamiento “¿cuál es la relación del segmento grande con el deslizador?”, planteada por la persona aplicadora. Por tanto, se considera una interacción del tipo estudiante-estudiante, estableciendo una negociación respecto al papel del deslizador en relación con los segmentos. El componente involucrado es el estudiantil, pues los intercambios son entorno a conocimientos previos del alumnado y que se refieren a las relaciones multiplicativas.

Como se ha mencionado, la intención de esta interacción se relaciona con la corrección, lo cual permite observar un vínculo entre el nivel incompleto y el preproporcional, pero ¿de qué forma? En la primera línea de la interacción el participante E-4.1 considera que la relación entre el deslizador y el segmento de mayor tamaño está dada por “ocho veces más”, razonamiento incorrecto, pues hace uso de los datos observados en las medidas, pero la relación propuesta no integra la proporcionalidad original, por lo que pertenece al nivel incompleto. Después de dicha sugerencia, les pregunta a sus pares: “¿ocho por cuánto te da 24?”, este cuestionamiento se refiere a un razonamiento cuantitativo que puede ser ubicado en el nivel preproporcional, ya que logra comprender que el producto entre el valor del deslizador y el segmento puede generar información para comprender la relación entre ambos.

A partir del cuestionamiento de E-4.1, E-4.4 comparte el resultado de dicha multiplicación. Al principio E-4.1 duda un poco porque en momentos anteriores aseguraba que 8 por 4 daba como resultado 24; termina por aceptar el resultado y E-4.3 concluye con una propuesta correspondiente al nivel preproporcional: “son 3, 3 veces”, refiriéndose a 3 como el factor multiplicativo que regula el caso particular cuando el deslizador mide 8 y el segmento mayor 24.

Como se puede observar, en una interacción tan breve pueden estar relacionados dos niveles que demandan una carga cognitiva muy diferente; por un lado, un razonamiento incorrecto y, por el otro, uno que establece un factor multiplicativo, pero ambos en función de la misma relación. Respecto a los componentes, lo contextual implica una carga importante en la delimitación de razonamientos, pues el alumno E-4.1 era de segundo año y el E-4.4 de primero; aunque es cierto que la corrección no implica grandes diferencias, sin duda tuvo un lugar muy importante en la relación proporcional. Estos intercambios se atribuyen a la rica diversidad presente en las aulas unitarias.

Evolución de razonamiento proporcional

Si bien este estudio no tiene un enfoque didáctico, esta categoría presenta hallazgos en los aprendizajes, porque además de identificar relaciones entre niveles, integra una diversidad de razonamientos que evidencia una evolución; es decir, hay un razonamiento inicial y es diferente con el que se concluye, evolución que se dio por las interacciones entre las personas participantes, como respuesta a la interacción en el micromundo, a partir de las intervenciones por parte de quien investiga o la activación de saberes previos del estudiantado.

Esta categoría es la más compleja debido a que integra elementos de la escuela unitaria como la diversidad de experiencias o saberes y el desarrollo de los componentes de un micromundo, sin dejar de lado la potencialidad de las actividades para desarrollar diferentes razonamientos, lo cual evidencia nuevamente que los niveles no están determinados por elementos como la edad, el grado escolar o el tipo de tarea a resolver, sino que es un fenómeno más complejo. Las evoluciones identificadas son de incompleto a preproporcional, cualitativo a preproporcional y preproporcional a proporcional.

Evolución incompleto-preproporcional

La primera evolución corresponde al razonamiento incompleto y al nivel preproporcional, en donde se comienzan a establecer relaciones multiplicativas. Una aclaración importante respecto a la evolución entre niveles es que no necesariamente se debe pasar por los niveles intermedios; por ejemplo, en esta evolución no se evidencia que el grupo de estudiantes se involucren en razonamientos cualitativos o aditivos, sino que de manera directa modifican su razonamiento a uno más sofisticado, tal como se muestra en la siguiente interacción de la actividad 3 (figuras 11 y 12).

E-2.1: Esperen, a ver si funciona /abre función de segmento de longitud dada/ ¿cuánto mide esta? Mide de 20, entonces es 10.

E-2.2: Pero así no va a salir E-2.1.

E-2.1: Yo digo/Elimina el 10, y el segmento es igual a “A” /.

E-2.2: Pues salió lo mismo.

E-2.1: Sí, pues sí voy a intentar así/Abre el menú del segmento de longitud dada y coloca a10/.

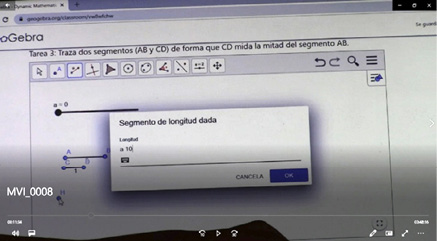
Figura 11. Actividad 3. Exploración para trazar el segmento, primer intento (incorrecto). Evolución incompleto-preproporcional

Ap: ¿Por qué “a10”?

E-2.1: Porque es la mitad de este/Señala al deslizador/.

Ap: A ver, ponlo así, a ver qué te da/Activa el segmento de longitud dada/.

Ap: Si te dio el de acá abajo. A ver, ponlo en 1 por ejemplo/E-2.1 lo realiza/Ok, ¿cuánto te vale este?

E-2.1: Uno.

Ap: Y ¿este?

E-2.1: Diez. Entonces tendría que ser 0.5.

Ap: A ver, chequen.

E-2.1: Borra primero ese.

E-2.2: A ver/E-2.1 traza el nuevo segmento de longitud dada/.

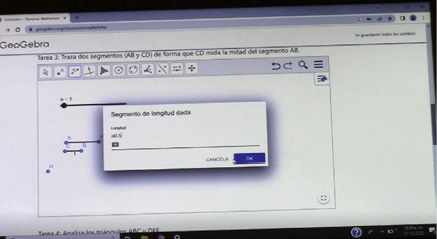
Figura 12. Actividad 3. Exploración para trazar el segmento, segundo intento (correcto). Evolución incompleto-preproporcional

E-2.1: Ahí está, la mitad de ese/Comparando con el otro segmento/Mira, si es la mitad este llega a 10.

Ap: ¿Qué pasó?

E-2.1: Le pusimos por 0.5 y ya quedó a la mitad.

Ap: A ver, ahí está en 5, y ¿este?

E-2.2: En 2.5.

Ap: ¿Cómo le hicieron?

E-2.2: Le pusimos “a0.5”.

Ap: ¿a0.5? Ahí, ¿por qué sería por 0.5?

E-2.2: Porque era la mitad de 1, de lo del deslizador.

La interacción se puede dividir en tres partes: exploratoria (nivel incompleto), consecutiva (evolución al razonamiento preproporcional) y resolutiva (razonamiento preproporcional consolidado).

Exploratoria. En la búsqueda de herramientas, procedimientos o hipótesis que pudieran ayudar a construir la relación entre dos segmentos. El participante E-2.1 comenta: “¿cuánto mide esta? Mide de 20, entonces es 10”, después interactúa con el menú de la herramienta segmento de longitud dada, en donde coloca “a10”. En este primer acercamiento se evidencia un razonamiento incompleto, pues al introducir “a10”, la razón que se obtendría sería de 10:1, razón que no cumple con el objetivo de la actividad.

Ante la posible solución, el aplicador pregunta “¿Por qué “a10”?”, a lo cual E-2.1 responde “porque es la mitad de este” y señala al deslizador. En ese momento específico el deslizador tenía un valor de 20, por lo que se aprovechan de este para determinar el tamaño del otro segmento que sería 10. La dificultad consiste en el manejo de herramientas del micromundo, pues saben que el nuevo segmento debe medir la mitad, pero no logran identificar de qué forma deben integrar los datos en las herramientas relacionadas.

Consecutiva. Después de que el equipo diseñó un segmento a partir de la razón 10:1, la persona aplicadora pregunta por los valores de ambos segmentos, a lo cual responden 1 y 10, y el alumno E-2.1 menciona: “entonces tendría que ser 0.5”. A través de las ayudas indirectas de la persona aplicadora, el estudiantado pudo reconocer que el factor multiplicativo necesario era de 0.5, identificando este momento como la evolución del razonamiento incompleto al preproporcional, y gracias a la exploración desde el razonamiento incompleto pudieron modificar el factor multiplicativo para obtener los dos segmentos en una relación 0.5:1.

Resolutiva. A partir de la trasformación de razonamiento, las personas integrantes del equipo trazan el nuevo segmento con la herramienta de longitud dada, definiéndolo como “a0.5”, así se logró identificar que se conserva la relación establecida a partir del deslizador. El alumnado compartió con la persona aplicadora que se integró el 0.5, a lo cual se preguntó “¿por qué sería por 0.5?”; la respuesta fue: “porque era la mitad de 1, de lo del deslizador”. De acuerdo con la última respuesta es que llega solo hasta un razonamiento preproporcional, pues, toma como referencia el valor de 1 del deslizador para relacionarlo con el factor multiplicativo de 0.5, lo cual no es evidencia de que logren identificar que el 0.5 no solo regula cuando el valor del deslizador es 1, sino también en todos los casos posibles según el valor máximo del deslizador.

En conclusión, en esta evolución las ayudas indirectas de la persona aplicadora y el componente técnico determinaron el cambio de razonamiento, pues hacen uso del lenguaje que proporciona GeoGebra y, a su vez, se brinda preguntas que permiten reafirmar sus procedimientos.

Evolución preproporcional–proporcional

Para la evolución del nivel preproporcional al proporcional se identifica el siguiente fragmento de la actividad dos:

E-2.1: Se engrandece tres veces más.

E-2.2: Es como si se multiplicara el 8 por 3, porque cuando estaba en 1/el deslizador/esta media uno/segmento pequeño/y esta media tres/segmento grande/entonces es el triple

Se identifica un intercambio entre dos participantes, por lo que la interacción es estudiante-estudiante, y se considera una interacción resolutiva de la actividad, ya que en la última línea se puede identificar la relación entre los segmentos.

¿Cuál es la diferencia entre “se engrandece tres veces más” y el análisis que establece la alumna E-22?, mientras que en la primera situación hace referencia a que se agrande 3 veces más a partir de la relación entre 8 y 24 hecha con anterioridad. En el planteamiento de la alumna E-2.2 se visualiza la existencia de la igualdad de razones, pues primero menciona “es como si se multiplicara el 8 por 3”, comparando a cuando “estaba en 1, está media uno y está media tres”, ideas que se pueden expresar de la siguiente manera: 24/8=3/1.

Si bien, la alumna no lo expone de esa manera, reconoce que la misma razón será funcional para todos los casos posibles que se logren establecer con el deslizador. En esta ocasión la evolución de nivel dependió de los intercambios de experiencias y saberes descubiertos a partir de la situación; es decir, el micromundo favoreció a la actividad cotidiana del alumnado: el aula unitaria.

En síntesis, la evolución de niveles se da a partir de las situaciones que ofrece el micromundo y las interacciones entre el estudiantado y las intervenciones de la persona aplicadora, es decir, el micromundo (contemplando todos sus componentes), generan oportunidades de aprendizaje de manera simultánea y acordes al objetivo del proyecto, pero este, a su vez, se traduce en el desarrollo de razonamientos más elaborados.

La evolución de niveles es una prueba de que el estudiantado puede razonar de manera distinta dependiendo de la situación, las herramientas empleadas e inclusive los intercambios entre pares; en otras palabras, los niveles no son mutuamente excluyentes y pueden existir transformaciones durante la misma resolución de las actividades sin brindar una enseñanza directa.

Conclusiones

Uno de los hallazgos más importantes del trabajo fue evidenciar que los niveles se pueden relacionar por diferentes motivos, tales como justificar procedimientos incorrectos a partir de una corrección, plantear argumentos más sencillos para explicar razonamientos más complejos y como medio de comprobación. A partir de ello, se identificó que todos estos motivos de relación tienen en común el tratar de complementar un razonamiento principal, es decir, que uno de los niveles está en función de otro, por ejemplo, en el caso de la explicación de razonamientos más demandantes como el preproporcional o proporcional, los razonamientos de menor actividad matemática como el aditivo o cualitativo se encuentran en función a los primeros. En síntesis, la relación de niveles favorece procesos como la justificación, corrección, explicación y comprobación de situaciones proporcionales.

Similar a la relación entre niveles, fue la evolución de un nivel inicial a otro más complejo. Si bien, se ha manifestado que no era un objetivo desarrollar nuevos aprendizajes o razonamientos en las personas participantes, fue una situación que se dio de manera natural de acuerdo con las condiciones en las que se desarrolló la implementación de las actividades, lo cual dio lugar a interacciones que evidencian cómo se va formalizando el RP, partiendo de nociones incorrectas, para luego generar negociaciones entre pares e incluso llegar a un razonamiento proporcional.

Estos aportes (relación y evolución entre niveles) puede compararse con lo que definen Karplus et al. (1983) como estrategias de respaldo, las cuales indican que un alumno o alumna puede utilizar estrategias de diferentes niveles en problemas de proporciones de diversa dificultad; por ejemplo, puede usar una estrategia multiplicativa en un problema con razones de números enteros, mientras que en uno con razones que contienen números racionales puede hacer uso de un razonamiento aditivo.

De la misma manera, Öztürk et al. (2021) reportan que las habilidades de razonamiento proporcional difieren según el tipo de problemas. Ambos aportes también guardan relación con lo que se definía como localidad en el marco teórico, en donde se expresaba que el razonamiento del alumnado es cambiante.

No obstante, ¿en qué radica la diferencia entre los aportes previos y los observados en este trabajo? Se considera que la diferencia principal consiste en que mientras Karplus y Öztürk reportan la existencia de una diversidad de razonamientos en diferentes situaciones, en este estudio se evidencia que, incluso para atender una misma situación, los alumnos pueden recurrir a diferentes razonamientos, o que una misma actividad puede generar un desequilibrio respecto al razonamiento con el que comenzaron a analizar la situación, llevándolos a la exploración de nuevos razonamientos. De tal manera se puede formalizar los saberes con lo que ya contaban o modificarse.

En cuanto a la relación y evolución de niveles, estos se asocian a las ventajas que ofrecen las aulas multigrado, tales como el aprendizaje colaborativo y el ser un espacio en donde todos los saberes, experiencias, habilidades y actitudes tienen cavida. Además, como lo reporta Santos (2006), Boix (2011), Corro y Bolaños (2018) y Block et al. (2015), en las interacciones vividas dentro de un aula unitaria, se negocian los significados, se priorizan las ayudas y se observan roles de tutoría como apoyo a los que tienen mayores áreas de oportunidad.

Se considera que aulas unitarias representan una riqueza para los estudios exploratorios como este, en donde se puede concluir que las interacciones entre pares propician el compartir los razonamientos, así como cuestionarlos y generar razonamientos sólidos y colectivos aplicados a los aspectos culturales y sociales propios de entorno de cada estudiante, tal cual lo expone el paradigma construccionista.

Finalmente, es importante mencionar que las interacciones generadas en el micromundo permitieron caracterizar el RP del alumnado participante y poder llegar a conclusiones como las descritas en las líneas anteriores.

Consentimiento informado

Se resguardó la información personal de las personas participantes mediante un consentimiento informado firmado por los padres y las madres de los y las estudiantes participantes.

Conflicto de intereses

Los autores declaran no tener algún conflicto de interés.

Declaración de la contribución de los autores

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo.

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: C.A.L.L 50 %, E.G.T. 30 % y S.A.P.P. 20 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente [C.A.L.L], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://doi.org/10.5281/zenodo.8350673

Referencias

Barros, A. y Stivam E. (2012). O software GeoGebra na Concepção de Micromundo. Revista Do Instituto GeoGebra Internacional De São Paulo, 1(1), 184-194.

Block, D., Ramírez, M. y Reséndiz, L. (2015). Las ayudas personalizadas como recurso de enseñanza de las matemáticas en un aula multigrado. Un estudio de caso. Revista Mexicana de Investigación Educativa, 20(66), 711-735.

Boix, R. (2011). ¿Qué queda de la escuela rural? Algunas reflexiones sobre la realidad pedagógica del aula multigrado. Profesorado. Revista de Currículum y Formación de Profesorado, 15(2), 13-23.

Bustos Jiménez, A. M. (2013). El espacio y el tiempo en la escuela rural: algunas consideraciones sobre la didáctica multigrado. Investigación en la escuela, 79, 31-41.

Butto, C., Fernández, J., Araujo, D. C. y Ramírez, A. I. (2019). El razonamiento proporcional en educación básica. Horizontes Pedagógicos. https://doi.org/10.33881/0123-8264.hop.21204

Corro, E. S. L. y Bolaños, D. J. (2018). La relación tutora entre estudiantes en una clase multigrado de México. Nodos y Nudos, 6(45), 27-40.

Fernández V. C. y Llinares C. S. (2012). Características del desarrollo del razonamiento proporcional en la educación primaria y secundaria. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 30(1), 129-142. https://doi.org/10.5565/rev/ec/v30n1.596

Flores, R. C. y Albarrán, A. M. R. (2008). La Telesecundaria, ante la sociedad del conocimiento. Revista Iberoamericana De Educación, 44(7), 1-11. https://doi.org/10.35362/rie4472187

García, E., Santiago, F. y Zepeda, G. (2019). Enseñanza de las matemáticas en escuelas multigrado y telesecundarias. En S. Otten, A.G. Candela, A. de Araujo, C. Haines y C. Munter (Eds.), Proceedings of the forty-first annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. (pp. 1751-1755). St Louis, MO: University of Missouri.

Godino, J. y Batanero, C. (2003). Proporcionalidad y su didáctica para maestros. Departamento de didáctica de las matemáticas. Universidad de Granada. 412-443.

Healy, L. y Kynigos, C. (2010). Charting the microworld territory over time: design and construction in mathematics education. Zdm–Mathematics Education, 42(1), 63-76. https://doi.org/10.1007/s11858-009-0193-5

Heller, P., Ahlgren, A., Post, T., Behr, M. J. y Lesh, R. (1989). Proportional reasoning: The effect of two context variables, rate type, and problem setting. Journal of Research in Science Teaching, 26(3), 205-220. https://doi.org/10.1002/tea.3660260303

Hoyles, C. y Noss, R. (1987). Synthesizing mathematical conceptions and their formalization through the construction of a Logo-based school mathematics curriculum. International Journal of Mathematical Education in Science and Technology, 18(4), 581-595. https://doi.org/10.1080/0020739870180411

Karplus, R., Pulos, S. y Stage, E. (1983). Proportional reasoning of early adolescents. En R. Lesh y M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 45-90). Nueva York: Academic Press.

Lamon, S. J. (2020). Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers. wi.org/10.4324/9781003008057

Lesh, R., Post, T. R. y Behr, M. (1988). Proportional reasoning. En M. Behr y J. Hiebert (Eds.), Number concepts and operations in the middle grades (pp. 93-118). National Council of Teachers of Mathematics, Lawrence Erlbaum Associates.

Mejoredu. Comisión Nacional para la Mejora Continua de la Educación. (2022). Indicadores nacionales de la mejora continua de la educación en México. Cifras del ciclo escolar 2020-2021.

Mochón, S. (2012). Enseñanza del razonamiento proporcional y alternativas para el manejo de la regla de tres. Educación Matemática, 24(1), 133-157.

Modestou, M. y Gagatsis, A. (2010). Cognitive and Metacognitive Aspects of Proportional Reasoning. Mathematical Thinking and Learning, 12(1), 36-53. https://doi.org/10.1080/10986060903465822

Noss, R. y Hoyles, C. (2019). Micromundos, Construccionismo y Matemáticas. Educación Matemática, 31(2), 7-21. https://doi.org/10.24844/em3102.01

Öztürk, M., Demir, Ü. y Akkan, Y. (2021). Investigation of Proportional Reasoning Problem Solving Processes of Seventh Grade Students: A Mixed Method Research. International Journal on Social and Education Sciences, 3(1), 48-67. https://doi.org/10.46328/ijonses.66

Rizo, M. (2006). La interacción y la comunicación desde los enfoques de la psicología social y la sociología fenomenológica: breve exploración teórica. Análisis: Cuadernos de comunicación y cultura. ISSN 0211-2175, 33, 45-62.

Sánchez, E. (2013). Razones, proporciones y proporcionalidad en una situación de reparto: una mirada desde la teoría antropológica de lo didáctico. Revista latinoamericana de Investigación en Matemática Educativa, 16(1), 65-97.

Santos, L. (2006). Atención a la diversidad: Algunas bases teóricas de la didáctica multigrado. Quehacer educativo, 75, 72-79.

SEP (2017). Aprendizajes clave para la educación integral. SEP.

Weir, S. (1987). Cultivating Minds: A Logo Casebook. HarperCollins Publishers.

---

1. 1* Corresponding authors

   Carlos Alberto Lugo Lugo, clugo26@alumnos.uaq.mx, https://orcid.org/0009-0004-9231-4812

   Erika García Torres, erika.garcia@uaq.edu.mx, https://orcid.org/0000-0003-1764-7380

   Santiago Alonso Palmas Pérez, s.palmas@correo.ler.uam.mx, https://orcid.org/0000-0003-1175-5938

   Facultad de Psicología y Educación, Universidad Autónoma de Querétaro, Querétaro, México.

1. 2 Departamento de Estudios Culturales, Universidad Autónoma Metropolitana, Lerma, México.