Implementación de extensiones simbólicas al lenguaje SQL en servidores de bases de datos objeto-relacionales

Implementation of SQL Symbolic Extensions on Object-Relational Database

Johnny Villalobos-Murillo

jvillalobos@una.cr

Escuela de Informática, Universidad Nacional.

Heredia, Costa Rica.

Steven Brenes-Chavarría

sbrenes@una.cr

Escuela de Informática, Universidad Nacional.

Heredia, Costa Rica.

Recibido-Received: 28/may/2014  /  Aceptado-Accepted: 21/ago/2014 /  Publicado-Published: 31/jul /2015.

Resumen

Este artículo propone extender el lenguaje SQL al crear nuevos tipos de datos con sus respectivos operadores, que permitan crear y manipular objetos simbólicos directamente sobre las bases de datos. La funcionalidad de la extensión propuesta se valida realizando transformaciones de datos relacionales clásicos a objetos simbólicos en bases de datos de gran volumen. Para los usuarios no familiarizados con el lenguaje SQL, se construye una interfaz de usuario final, que facilita y guía el proceso de transformación simbólica.

Palabras claves: Base datos; extensión; objeto-relacional; objeto simbólico;  SQL.

Abstract

This article proposes extend the SQL language with new data types and operators for create and manipulate symbolic objects directly in the database. The functionality of the proposed extension is validated by performing transformations of classical symbolic objects to relational data bases of large data. For users not familiar with the SQL language, a final user interface is built to facilitate and guide the process of symbolic transformation.

Keywords: Database; extension; relational-object; SQL; symbolic-object.

Actualmente, los grandes volúmenes de información almacenada presentan dificultades para su manipulación y para la extracción del conocimiento contenido en las bases de datos. Este motivo ha llevado a muchos investigadores de diversos campos, entre los que destacan la estadística y la computación, a enfocar sus esfuerzos para simplificar las tareas de reducción, extracción y análisis de datos.  Un ejemplo de este tipo de investigaciones es el proyecto SODAS (Bock H-H & Diday E, 2000) donde se propone la creación y utilización de un nuevo tipo de dato llamado objeto simbólico, el cual se obtiene a partir de bases de datos relacionales (Codd, 1970).

El objeto simbólico puede considerarse como un mecanismo que permita la extracción y agrupación de datos contenidos en bases de datos relacionales. A partir de él, se han modificado algunos métodos de análisis de datos clásicos y se han desarrollado nuevos métodos de análisis simbólico. Tal es el caso de la modificación realizada al algoritmo de análisis de componentes principales para aplicarse a objetos simbólicos (Rodríguez, 2000). Además, se han creado herramientas computacionales para transformar datos clásicos en datos simbólicos; la herramienta Data Bases to Symbolic Object (DB2SO, por sus siglas en inglés) del proyecto SODAS es una de ellas.

Los objetos simbólicos producidos por estas herramientas se usan exclusivamente como insumos de los métodos de análisis simbólico, esto hace  que no sea posible manipularlos ni utilizarlos en otras áreas de investigación. Con el propósito de solventar esta limitación, nuestra investigación se propuso desarrollar una extensión para el lenguaje SQL. La finalidad es crear y manipular objetos simbólicos con la misma facilidad que presentan los tipos de datos propios de una base de datos, para así extender el uso de estos objetos simbólicos a múltiples áreas de investigación.

Esta investigación propone el diseño e implantación de una extensión para el lenguaje SQL que utilice algoritmos de transformación de datos clásicos a datos simbólicos, el diseño de las estructuras de datos y los operadores necesarios para su persistencia y manipulación en sistemas gestores de bases de datos. Por otro lado y pensando en aquellos usuarios que no estén familiarizados con el lenguaje SQL, se desarrolla una interfaz gráfica que utiliza la extensión propuesta para facilitar el proceso de transformación. La extensión y la interfaz se ponen a disposición como software libre en el sitio WEB del Laboratorio de Bases de Datos de la Universidad Nacional de Costa Rica (www.slinfo.una.ac.cr), contribuyendo, de esta forma, con el libre acceso a las tecnologías de información.

Este artículo está compuesto de cuatro apartados. El primero de ellos estudia formalmente el concepto del objeto simbólico, así como las definiciones matemáticas más importantes. El segundo presenta la extensión simbólica propuesta, lo que incluye los componentes, funciones y sintaxis definida para su utilización en bases de datos. En el tercer apartado se realizan las pruebas de transformación para convertir datos clásicos a datos simbólicos. En el cuarto y último apartado se exponen las conclusiones de esta investigación. 

Objetos simbólicos

En esta sección se presentan las definiciones formales y ejemplos de los objetos simbólicos. Los objetos simbólicos pueden ser obtenidos de diversas fuentes,  una de las más frecuentes es las tablas de bases de datos relacionales.  En la tabla 1, se muestra un ejemplo de datos clásicos que corresponde a un conjunto de observaciones Ω, donde cada tupla de la tabla corresponde a un individuo particular.

Tabla 1

Representación de datos clásicos

Definición 1: Un concepto C es el resultado de una intensión I sobre una extensión E. La intensión es el deseo de encontrar conjuntos de datos a partir de las propiedades de las variables que interesan ser agrupadas y analizadas. La extensión, por su parte, es el conjunto de todos los individuos que cumplan con la intensión.

Suponga el concepto  C [A, C] con I (A > 1.5, 33≤ B ≤ 36), el resultado es un subconjunto del producto cartesiano , que cumple con la intensión I y su correspondiente extensión  E. Se genera la tabla 2 como resultado de aplicar sobre la tabla 1 el concepto C.

Tabla 2

Representación de un concepto

Una definición no formal  establece que los objetos simbólicos se obtienen como el resultado de realizar agrupaciones de datos clásicos en variables simbólicas según un concepto.

Objeto-simbólico  → [Concepto] {variables simbólicas,….}

Definición 2: Un vector descriptor    es el conjunto de variables de cada individuo de la tabla de observaciones. La tabla de observaciones representa el origen de datos clásicos, tome como ejemplo la tabla 1 de la cual se pueden extraer los vectores descriptores , para los respectivos individuos e en

Definición 3: Una relación es una asociación de un vector descriptor d con una variable ,  se puede escribir de la forma . La relación toma la forma de .

Definición 4: Un objeto simbólico es la tripleta , donde es una función de aserción , dicha función mapea cada vector descriptor del individuo i del conjunto de observaciones Ω al conjunto .

Definición 5: Un objeto simbólico se clasifica en binario si es decir, a es un mapeo binario, entonces, s es un objeto simbólico binario.

Definición 6: Un objeto simbólico se clasifica en modal si , es decir, a es un mapeo modal, entonces, s es un objeto simbólico modal.

Clasificación de los objetos simbólicos

Basándose en la cardinalidad del conjunto de las variables que definen su concepto, los objetos simbólicos pueden ser clasificados como objetos de primer orden, segundo orden u orden superior (Diday, 2009).

Definición 7: Los objetos simbólicos son de primer orden cuando el concepto se refiere a individuos (una sola variable). Un objeto simbólico es de segundo orden o superior cuando el concepto está formado por clases (dos o más variables).

En la tabla 3 se muestra un objeto simbólico de primer orden tomando como referencia la tabla 1. En la tabla 4 se observa un objeto simbólico de orden superior .

Tabla 3

Objeto simbólico de primer orden

Tabla 4

Objeto simbólico de orden superior

Variables simbólicas

Una variable simbólica es una representación particular que permite agrupaciones por conceptos. Las variables se clasifican en multivaluada, intervalos e histograma.

Definición 8: Una variable multivaluada Y es aquella en la que los posibles valores que representa la variable simbólica  son tomados del dominio del concepto. La lista completa de posibles valores es finita y los valores son definidos como valores no categóricos, es decir, cuantitativos. La tabla 5 muestra una columna llamada multivaluada, en donde por cada valor agrupado del concepto se cuenta la cantidad de veces que aparece dicho término en la agrupación.

Tabla 5

Ejemplo de

Definición 9: Una variable intervalo es aquella cuyos valores son definidos como , con el intervalo puede ser abierto o cerrado   En la tabla 6 se observan los diversos intervalos, según la agrupación del concepto (Moore, 1979).

Tabla 6

Objeto simbólico de orden superior

Definición 10: Una variable histograma Y toma posibles valores sobre el dominio . Sea el posible dominio de una variable multivaluada , con entonces, una variable modal multivaluada es aquella que toma sus valores del subconjunto de con valores no negativos asociados a los valores del subconjunto, para una observación de una categoría toma la forma:

Donde   y donde aparece como el peso , y con En la tabla 7 se muestran las distintas frecuencias de aparición del término.

Tabla 7

Objeto simbólico de orden superior

Extensión simbólica

Debido a que los  sistemas gestores de bases de datos no poseen las funcionalidades requeridas para crear, almacenar y manipular los objetos simbólicos, se propone implementar la extensión simbólica al lenguaje SQL para el sistema gestor de base de datos libre PostgreSQL (The PostgreSQL Global Development Group, 2012), el cual permite hacer modificaciones en sus programas fuentes.  Una extensión, en general, para una base de datos, amplía el lenguaje SQL con nuevas directrices, tipos de datos, operadores y funciones. Para comprender mejor la dimensión de la extensión se muestra en la figura 1 su arquitectura conceptual.

Figura 1. 

Arquitectura conceptual de la extensión simbólica.

Fuente: propia del estudio.

La arquitectura conceptual de la extensión establece tres grupos de componentes. El primer, constituido por las estructuras necesarias de datos para registrar en la base de datos las variables simbólicas. Cada estructura se crea como un tipo de dato base, esto quiere decir que formará parte de los tipos primitivos del sistema gestor de base de datos.  Los nuevos datos requieren de operadores aritméticos, operadores relacionales y operadores estadísticos. Las funciones en la extensión se clasifican en:

1. Interfaz: Funciones para establecer los formatos de entrada y salida del tipo de dato.
2. Constructor: Construyen los diferentes tipos de datos realizando agrupaciones.
3. Aritméticas: Permiten construir los operadores aritméticos para los diferentes tipos de datos.
4. Relación: Permiten construir los operadores relacionales para los diferentes tipos de datos.

En la tabla 8 se muestra en detalle los tipos de datos, los operadores y funciones para los tipos de datos intervalo.

Tabla 8

Componentes de  la extensión simbólica para tipos intervalo

Fuente: propia del estudio.

Se crean, además de las funciones para los tipos de datos, otras funciones para construir los objetos simbólicos que transforman las variables seleccionadas a conceptos y su intensión. La función symbolic_object() es la encargada de la transformación. El  algoritmo general se muestra en la siguiente figura 2.

Figura 2.

Algoritmo para construcción de datos simbólicos.

Fuente: propia del estudio.

Pruebas funcionales a la extensión simbólica

Para realizar las pruebas de funcionalidad se ha creado una tabla relacional basada en el ejemplo Medical (Billard, 2006) y extendida a 600.000 observaciones. En esta tabla se han registrado las variables médicas de exámenes aplicados a personas de diferente sexo y edad, con datos de cirugías realizadas en ellos. Las pruebas tienen el objetivo de corroborar el funcionamiento y ejemplificar el uso sintáctico de la gramática de la extensión. En la tabla 9 se especifica el esquema de la tabla Medical.

Tabla 9

Tabla relacional Medical

Nota: Symbolic Data Analysis: Conceptual Statistics And Data Mining (Billard, 2006).

Fuente: propia del estudio.

Ejemplo 1: Construcción de un concepto. Utilizando la tabla medical se construye un concepto con las categorías de sexo y edad del paciente. Formalmente el concepto del ejemplo se representa por . En el código 1 se crea el concepto s.

Código 1. Creación de un concepto

select create_symbolic_object ('medical','sexo,edad');

Como se aprecia en el código 1, es necesario invocar la función create_symbolic_object, la cual recibe como primer parámetro el nombre de la tabla relacional (origen de datos) y como segundo parámetro los conceptos separados por comas “,”. En la tabla 10 se aprecia la ejecución de una vista llamada stable creada por la función create_symbolic_object del código 1.

Tabla 10

Construcción de un concepto

        Fuente: propia del estudio.

Ejemplo 2: Construcción de una variable simbólica de tipo intervalo. En este ejemplo interesa analizar los mínimos y máximos de la columna peso, estos valores deben ser agrupados por el concepto de segundo grado “sexo,edad”. Formalmente se conforma el objeto simbólico:

El objeto simbólico anterior se construye haciendo uso del código 2, en la tabla 11 se muestra el resultado de su ejecución.

Código 2. Creación de un intervalo simbólico

SELECT create_symbolic_object( 'medical', 'gender,age',

'SINT(PESO),SINT(PULSO)');

La ejecución del código 2 genera la tabla 11, donde la segunda columna es una variable intervalo simbólico (pesos mínimos y máximos de la categoría sexo y edad), de igual forma la tercera columna representa un intervalo simbólico para el pulso.

Tabla 11

Resultado de la construcción de intervalos

Fuente: propia del estudio.

Ejemplo 3: Construcción de una aserción. Algunas veces, con el fin de disminuir la población de datos, es conveniente aplicar reglas lógicas sobre los registros estas reglas se les llama una aserción. Este ejemplo particular aplica una aserción sobre todos los registros de Medical tales que la edad del paciente sea mayor a 93 años. La implementación de esta aserción se logra mediante la ejecución del código 3. Formalmente se define el objeto simbólico:

Código 3. Creación de una aserción

SELECT create_symbolic_object('medical', 'gender,age', 'sint(age)', 'age >= 93');

Como resultado de la ejecución del código anterior,  se construye la tabla 12 con el tipo de datos intervalo y su aserción. El resultado de la ejecución es la generación de una tabla con cinco registros nuevos, de tipo intervalos degenerados1.

Tabla 12

Resultado de crear una aserción

    Fuente: propia del estudio.

Ejemplo 4: Uso de operadores aritméticos para intervalos

Por otro lado, es necesario poder realizar operaciones aritméticas como sumar o restar intervalos. El objeto simbólico formado por la suma de dos intervalos simbólicos se define formalmente como:

Código 4. Operaciones aritméticas sobre intervalos

SELECT CONCEPT, SINT(PESO)+SINT(PULSO) FROM STABLE;

El resultado de ejecutar el código 4 genera la tabla 13, donde la segunda columna es el resultado de sumar el intervalo de peso más el intervalo de pulso. En la tabla 14 se tiene la lista completa de funciones aritméticas que soporta le extensión simbólica para los intervalos.

Tabla 13

Resultado de  ejecutar una suma entre intervalos

Fuente: propia del estudio.

Tabla 14

Operadores aritméticos para intervalos

Ejemplo 5: Uso de operadores relacionales para intervalos. De la misma forma, es útil poder comparar intervalos en términos de su relación de orden2. Suponiendo que un investigador necesita determinar si los intervalos de la presión sistólica son mayores o iguales que los intervalos de la presión diastólica, dicha intensión de investigación puede ser resuelta aplicando el código 5, dejando el resultado en la tabla 15.

Código 5. Operaciones relacionales sobre intervalos

select concept, sint(psistolica), sint(pdiastolica),

sint(psistolica)>sint(pdiastolica) from stable;

Tabla 15

Resultado de ejecutar operaciones relacionales

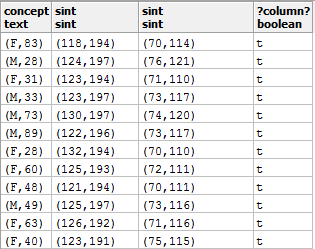
Fuente: propia del estudio.

La cuarta columna de la tabla 15 representa una variable booleana, siendo t (true, verdadero) como resultado de la operación de comparar el primer intervalo contra el segundo. En la tabla 16 detalla la lista de los operadores relacionales de intervalos.

Tabla 16

Operadores relacionales para intervalos

Ejemplo 6: Uso de operadores conjuntistas para intervalos. De la misma forma como se desarrollaron las funciones aritméticas y relacionales, la extensión también contempla las operaciones conjuntistas. Este ejemplo aplica la unión3 de intervalos, en la tabla 17 se muestra la ejecución del código 5. La tabla 18 se detalla todas las operaciones conjuntistas implementadas.

Código 6. Operaciones de conjuntos sobre intervalos

SELECT concept,unionSint( sint(psistolica),  sint(pdiastolica))from stable group by concept;

Tabla 17

Resultado de ejecutar un operador de unión sobre intervalos

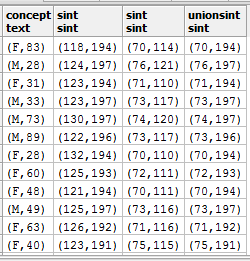
Tabla 18

Operadores relacionales soportados para intervalos

La extensión contempla otras funciones estadísticas, en la tabla 19 se observan el nombre de estas funciones implementadas para intervalos.

Tabla 19

Operadores estadísticos soportados para intervalos

Ejemplo 7: Construcción de una tabla simbólica. Una vez el investigador tenga la consulta SQL, la misma podrá ser guardada como una tabla simbólica mediante el código 7.

Código 7. Guardar una tabla simbólica

create table TablaEstudios as

select concept, sint(psistolica) col1, sint(pdiastolica)col2 from stable group by concept;

Herramienta de transformación de datos relacionales a datos simbólicos

En conjunto con la extensión simbólica pSymbolic, se desarrolló una aplicación informática para facilitar al usuario no experto la trasformación de datos relacionales a datos simbólicos. La misma puede ser descargada en la sección de software desde el sitio WEB www.slinfo.una.ac.cr. En la figura 3 se muestra la pantalla principal del aplicativo.

Figura 3.

Programa R2S, versión 1.0.

Fuente: propia del estudio.

El usuario después de escoger la fuente de datos puede observar los datos fuente mediante el botón “Sources table” y la tabla simbólica resultante con el botón “Symbolic table”. Para crear un dato simbólico, la interfaz le ayuda establecer las aserciones y la definición del concepto (ver figura 4).

Figura 4.

Selección del concepto.
Fuente: propia del estudio.

Para crear las variables simbólicas, se debe escoger en primera instancia la columna de la tabla relacional y luego el tipo de variable simbólica en la que se va convertir, el proceso finaliza pulsando el botón “Add” (ver figura 5).

Imagen 5.

Variables simbólicas.

Fuente: propia del estudio.

Se termina el proceso al seleccionar la opción “Symbolic table”, la cual despliega la información simbólica del siguiente objeto:

Figura 6.

Transformación simbólica, intervalo de peso.

Fuente: propia del estudio.

De forma similar se pueden agregar tantas variables simbólicas como el investigador requiera, para ejemplificarlo en la figura 7 se definieron dos datos simbólicos, la primera de tipo intervalo y la segunda un histograma.  Formalmente se definió el objeto simbólico:

Figura 7.

Transformación simbólica, histograma de pulso.

Fuente: propia del estudio.

Utilización de la extensión

El software se hospedó en el portal WEB www.slinfo.una.ac.cr (ver figura 8) donde el lector encontrará información sobre la extensión. Esta página está dividida en tres secciones: introducción, documentación y descarga. La sección de introducción contiene una breve información sobre las funciones de la extensión sin entrar en detalles.

Figura 8.

Página principal de la extensión.

Fuente: propia del estudio.

La segunda opción muestra un manual de usuario en línea, donde se detallan los pasos para ejecutar las transformaciones simbólicas. Los ejemplos que se encuentran son:

1. Creación de un concepto.
2. Construcción de una variable simbólica de tipo intervalo.
3. Construcción de una aserción.
4. Uso de operadores aritméticos para intervalos.
5. Uso de operadores aritméticos para intervalos.
6. Uso de operadores conjuntistas para intervalos.
7. Construcción de una tabla simbólica.

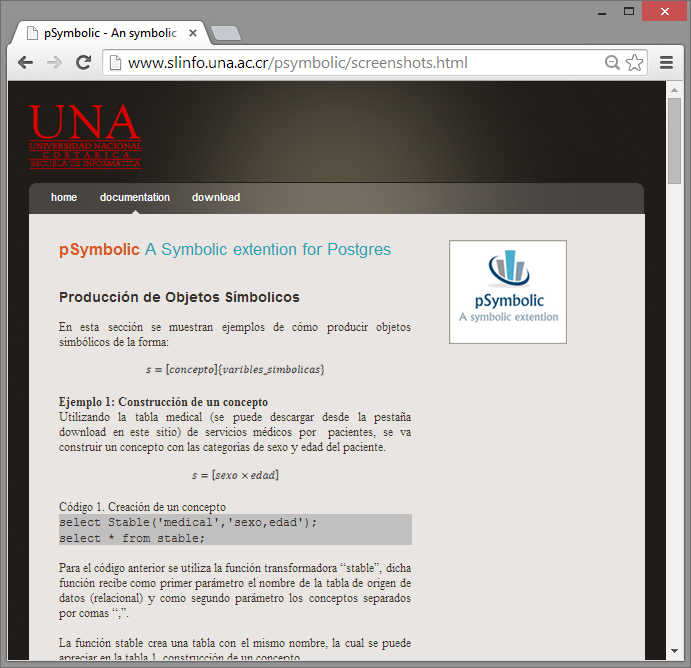
Figura 9.

Documentación de la extensión del sitio WEB.

Fuente: propia del estudio.

La pestaña de descargas permite obtener la extensión y la interfaz de trasformación de forma libre.

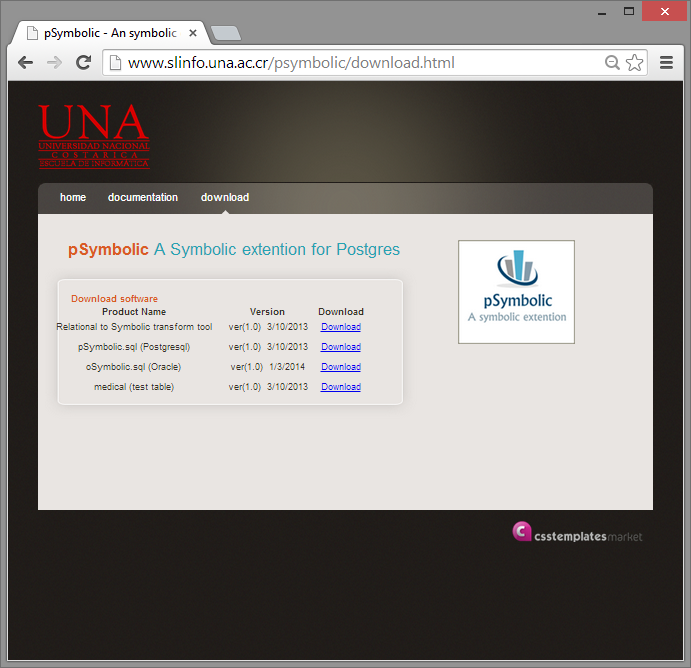
Figura  10.

Opción de descarga de la extensión.

Fuente: propia del estudio.

La extensión se implementó para los sistemas gestores de bases de datos PostgreSql y Oracle, permitiendo así que diferentes usuarios puedan utilizar la extensión y dando la posibilidad que los objetos simbólicos sean de libre utilización y permitanla posibilidad de incorporarlos en diferentes áreas de investigación y no solamente en el análisis de datos simbólicos.

Desde su publicación en el portal del Laboratorio de Bases de Datos de la Universidad Nacional a la fecha de esta publicación, se han descargado un total de 109 extensiones en los dos últimos meses. Los países que han realizo descarga del software se detallan en la imagen 11.

Figura 11.

Descargas de la extensión por país. Google Analytics a la fecha 26 de mayo del 2014.

Fuente: propia del estudio.

Conclusiones

Con la finalización de esta investigación, se desarrollaron una serie de productos publicados en los sitios oficiales de la Universidad Nacional, que permitieron aumentar la visibilidad de las investigaciones realizadas por la Escuela de Informática a nivel global.

De esta manera se publica, de forma gratuita, una extensión para el manejo de los datos simbólicos que son utilizables tanto para el sistema gestor Oracle como PostgreSQL. Esta extensión contempla funciones de construcción, visualización, aritméticas, estadísticas y lógicas.

Por otro lado, se facilita la descarga de una herramienta para el manejo de la extensión para aquellos usuarios de perfil no técnico. En consecuencia, se espera que el dato simbólico se conozca aún más al extender la tecnología de bases de datos en función de necesidades reales de los investigadores.

El proyecto de investigación 0281-13, “Implementación de extensiones simbólicas al lenguaje SQL en servidores de bases de datos objeto-relacionales” proyecto suscrito al Área de Investigación y formulado por el investigador Johnny Villalobos Murillo de la Escuela de Informática y Computación de la Facultad de Ciencias Exactas y Naturales de la Universidad Nacional de Costa Rica y sus colaboradores,  contribuye a disminuir la brecha tecnológica, el acceso libre a las tecnología de información y el quehacer de esta Universidad en función de la sociedad. 

La tecnología desarrollada puede ser un marco metodológico de apoyo a investigaciones en bases de datos. La creación de extensiones puede formar parte de contenidos de cursos avanzados en bases de datos. La extensión simbólica es una forma de reducir grandes volúmenes de datos tal y como se demostró en las pruebas funcionales, haciendo más manipulables los datos para el análisis de datos simbólicos mediante el uso de los nuevos operadores simbólicos.

Referencias.

Billard, L. (2006). Symbolic Data Analysis: Conceptual Statistics And Data Mining. New York: Wiley. DOI  http://dx.doi.org/10.1002/9780470090183

Bock, H-H., & Diday, E. (2000). Analysis of Symbolic Data. Exploratory methods for extracting statistical information from complex data. Springer Verlag, 425.

Codd, E. (1970). A relational model of data for large shared data banks. Communications of the ACM, 377-387. DOI  http://dx.doi.org/10.1145/362384.362685

Diday, E. (2009). The state of the art in symbolic data analysis: overview and future. Obtenido de http://media.wiley.com/product_data/excerpt/36/04700188/0470018836-1.pdf

Moore, R. (1979). Methods and Applications of Interval Analysis. Philadelphia, USA: Society for Industrial and Applied Mathematics (SIAM)

Rodríguez, O. (2000). The Knowledge Mining Suite (KMS). San José, Costa Rica: University of Costa Rica and Predisoft International S.A

The PostgreSQL Global Development Group. (2012). PostgreSQL Developer's Guide. Obtenido de http://www.postgresql.org

Implementación de extensiones simbólicas al lenguaje SQL en servidores de bases de datos objeto-relacionales  (Johnny Villalobos-Murillo y Steven Brenes-Chavarría) por Revista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported.

1 Un intervalo es degenerado si tiene la forma (Moore, 1979)

2 Se define para los intervalos la relación de orden  (Moore, 1979)

3 Se define la unión de intervalos como para intervalos de la forma