UNICIENCIA Vol. 30, No. 1, pp. 115-122. Enero-Junio, 2016.
URL: www.revistas.una.ac.cr/uniciencia
Email: revistauniciencia@una.cr
ISSN Electrónico: 2215-3470
DOI: http://dx.doi.org/10.15359/ru.30-1.7
Métodos de reducción de dimensionalidad: Análisis comparativo de los métodos APC, ACPP y ACPK
Dimensionality Reduction Methods: Comparative Analysis of methods PCA, PPCA and KPCA
Jorge Arroyo-Hernández
Escuela de Matemática
Universidad Nacional
Heredia, Costa Rica
Recibido-Received: 20/feb/2015 / Aceptado-Accepted: 8/may/2015 / Publicado-Published: 31/ene /2016.
Resumen
Los métodos de reducción de dimensionalidad son algoritmos que mapean el conjunto de los datos a subespacios derivados del espacio original, de menor dimensión, que permiten hacer una descripción de los datos a un menor costo. Por su importancia, son ampliamente usados en procesos asociados a aprendizaje de máquina. Este artículo presenta un análisis comparativo sobre los métodos de reducción de dimensionalidad: ACP, ACPP y ACPK. Se realizó un experimento de reconstrucción de los datos de formas vermes, por medio de estructuras de hitos ubicados en el contorno de su cuerpo, con los métodos con distinto número de componentes principales. Los resultados evidenciaron que todos los métodos pueden verse como procesos alternativos. Sin embargo, por el potencial de análisis en el espacio de características y por el método del cálculo de su preimagen presentado, el ACPK muestra un mejor método para el proceso de reconocimiento y extracción de patrones.
Palabras claves: Reducción de dimensionalidad, nube de datos, problema de la preimagen.
Abstract
The dimensionality reduction methods are algorithms mapping the set of data in subspaces derived from the original space, of fewer dimensions, that allow a description of the data at a lower cost. Due to their importance, they are widely used in processes associated with learning machine. This article presents a comparative analysis of PCA, PPCA and KPCA dimensionality reduction methods. A reconstruction experiment of worm-shape data was performed through structures of landmarks located in the body contour, with methods having different number of main components. The results showed that all methods can be seen as alternative processes. Nevertheless, thanks to the potential for analysis in the features space and the method for calculation of its preimage presented, KPCA offers a better method for recognition process and pattern extraction.
Keywords: Dimensionality Reduction; Points Clouds; Preimage problem.
En la actualidad, el creciente volumen de información generado por sistemas de información y comunicación derivados de investigaciones y procesos industriales demanda nuevas técnicas de manipulación de datos con el objetivo de extraer información no trivial que reside, de manera implícita, para facilitar la obtención de patrones y su análisis.
Sin embargo, evaluar esos millones de datos capturados en tiempo y espacio es altamente complejo, por lo que se busca algoritmos matemáticos que mejoren tiempos de respuesta; pero que, a su vez, la información intrínseca se pueda recuperar.
Por esto, es imprescindible contar con métodos de reducción de dimensionalidad (MRD) eficientes que permitan simplificar la descripción del conjunto de datos y que sean capaces de abarcar grandes volúmenes de información en tiempos prudenciales.
Los MRD son procedimientos que mapean el conjunto de datos a subespacios derivados del espacio original, de menor dimensión, en los que se encuentran en todo el conglomerado de la información, permiten una representación adecuada y significativa de estos y con un número pequeño de parámetros que logran evidenciar propiedades no observables (Lee y Verleysen, 2007). Como resultado de los MRD, se favorece la compresión, eliminación de redundancia del conjunto de datos y permite mejorar procesos de clasificación y visualización de los datos a un menor costo computacional.
El objetivo de este artículo es presentar un estudio comparativo de los MRD lineales y no lineales a partir del método de análisis de componentes principales (ACP). La primera parte de este abordará una descripción teórica de los métodos: ACP, ACP probabilístico y ACP con kernel. Para este último, se abordará el problema de la preimagen y una solución por medio de un método cerrado. Finalmente, se hará un análisis comparativo de los resultados obtenidos a partir de la aplicación de los métodos para la reconstrucción de los datos original con un menor número de dimensiones que las contendidas por el espacio de entrada de los datos.
Reducción de dimensionalidad y linealidad
Asimismo, para Van der Maaten, Postma, y Van den Herik (2007), los MRD son el proceso que transforma un conjunto de datos con dimensionalidad m a un nuevo conjunto Q con dimensionalidad m’ (m’<m), de forma tal que conserve la mayor información intrínseca posible; además, su principal distinción es que pueden ser desarrollados desde el supuesto o no de la linealidad.
A lo largo del desarrollo teórico de este documento se representará el conjunto de datos por medio de una estructura de matriz X ϵ Mmxn(
), donde m representa el número de muestras y n es el número de observaciones o mediciones por muestra.
Análisis de componentes principales
El análisis de componentes principales (ACP) es una técnica lineal que se utiliza para la eliminación de la redundancia de los datos (Schlens, 2005). Es ampliamente usado, sin embargo, su mayor limitación se basa en el supuesto de linealidad.
Para Schlens (2005), ACP permite un cambio de base a una de menor dimensionalidad sobre X a través de la ecuación de transformación Y = PX, donde P es una matriz ortogonal denominada matriz de representación. El objetivo es determinar la matriz P que permita que la nube de datos pueda ser proyectada a un espacio de menor dimensión.
La estrategia es buscar P de forma que se garantice la no correlación entre vectores de Y, es decir, Cij ϵ CY ,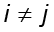 
sean nulos. Si la correlación entre las distintas muestras es nula, se elimina la redundancia y el subespacio de datos puede ser descrito por P. De lo contrario, cada entrada Cij que corresponda a valores grandes que representará alta redundancia de las observaciones i y j y, por ende, habrá el ruido presente.
Según el mismo autor, el algoritmo para hallar P inicia con el centrado y estandarizado de los datos. Luego, se calcula la matriz de covarianza de X,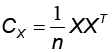 
, que es simétrica y diagonalizable, y que cuantifica la covarianza entre las mediciones. Luego, se obtiene los vectores propios de Cx, que son elegidos como columnas vectores de P, ordenados de acuerdo con el valor propio y que sirven de nuevas coordenadas del sistema donde es maximizada la varianza. Se elige el número adecuado de vectores propios que son denominados componentes principales y que describen la información del conjunto de datos de acuerdo con su coeficiente de inercia, el cual indica el porcentaje de esta, presente en cada componente principal.
Análisis de componentes principales probabilístico
El análisis de componentes probabilístico (ACPP), por Tipping y Bishop (1999), es una derivación del ACP basado en un modelo probabilístico de variable latente que relaciona el conjunto de datos X a un conjunto de menor dimensión expresado mediante la combinación lineal
t = W z + μ + ε
donde W relaciona el conjunto de datos original, Z es la variable latente, μ permite que el modelo posea media no nula y ε es el error o ruido del modelo.
El ACPP tiene como objetivo estimar la base W y su varianza σ2 a partir del conjunto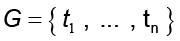 
. Para esto, en conjunción del modelo gaussiano isotrópico N (0, σ2 I) con un error ε , la ecuación del análisis factorial provee la distribución de probabilidad condicional sobre el espacio G dada por
p(t | z) ~ N(Wz+ μ, σ2I).
Con la distribución marginal sobre las variables latentes gaussianas y definidas por z~N (0, I), la distribución marginal de los datos observados t se obtiene integrando t ~N (μ, C) donde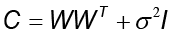 
. Su correspondiente verosimilitud logarítmica es
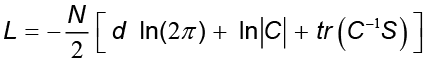
donde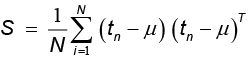 
. El estimador de probabilidad máxima para μ es dado por la media de los datos, en la cual S es la matriz de covarianzas de las observaciones G. De forma iterativa, W y σ2 pueden ser obtenidas maximizando la expresión
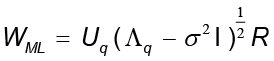
donde los vectores columnas de la matriz Uq son los vectores propios de S con los correspondientes valores propios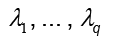 
almacenados en la matriz diagonal 
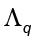, y R es una matriz arbitraria ortogonal de rotación. Además, si se toma W = WML, el estimador de máxima probabilidad para σ2 es dado por 
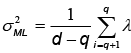la cual puede entenderse como la varianza perdida promediada sobre el número de componentes suprimidas. Para σ2 >0, los datos pueden ser recuperados por
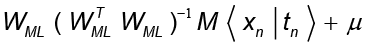
con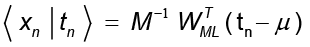 
.
Análisis de componentes principales con kernel y el problema de la preimagen
El análisis de componentes principales con kernel (ACPK) es un método para la reducción de dimensionalidad de los datos en el que se aplica el método de análisis de componentes principales sobre el espacio característico F (Scholkopfl, Smola y Müller, 1999).
Scholkolpfl et al. (1999) presentan un desarrollo a través de un método consiste en mapear el conjunto de datos de entrada (o espacio original de datos) al espacio de características, a través de una función kernel ф: 
N→F, x→, x→ф(x). Asumiendo que los datos son centrados, es decir,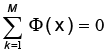 
se calcula la matriz de covarianza 
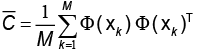en F. Luego, se calculan los valores propios 
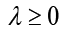y los vectores propios 
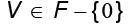de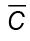 
que cumple 
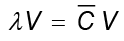. Las soluciones V se distribuyen en 
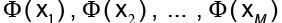. Al combinar los resultados, se obtiene
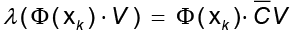y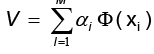 
con las cuales se construye la identidad:
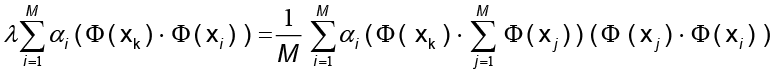para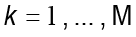 
.
Al definir la matriz K como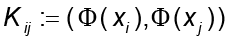 
, la identidad anterior se reexpresa
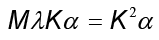donde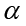 
denota el vector columna con entradas 
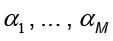. Al ser K una matriz simétrica que contiene el conjunto de vectores propios, la ecuación es simplificada en
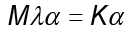y de esta se obtiene las soluciones
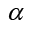de la ecuación anterior.
Luego, se normaliza los respectivos vectores propios para obtener las proyecciones de los estos en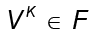
que son calculadas por
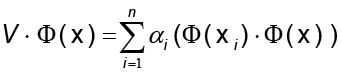
llamados componentes principales no lineales de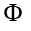 
en F.
Problema del cálculo de la preimagen en ACPK
En ACPK no siempre es posible el cálculo directo de los vectores preimágenes en el espacio de entrada 
N. El problema consiste en hallar una función invertible f que exprese la función kernel k de la forma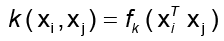 
para la cual sea posible calcular la preimagen exacta de la forma
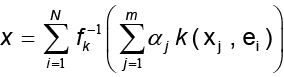
donde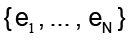 
una base ortonormal del espacio de entrada. De forma más precisa, el problema consiste en encontrar un método que reemplace la función f y que estime la mejor aproximación para x, suponga x* ϵ 
N , que satisfaga 
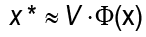con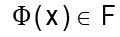 
.
El método de aproximación por mapas conformes de Honeine y Richard (2011) en conjunto con Arroyo y Alvarado (2014) permite determinar el cálculo de la aproximación de la preimagen mediante método cerrado
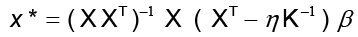
donde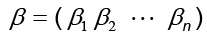 
y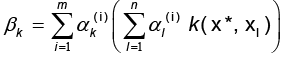 
para k = 1, ..., m y 
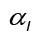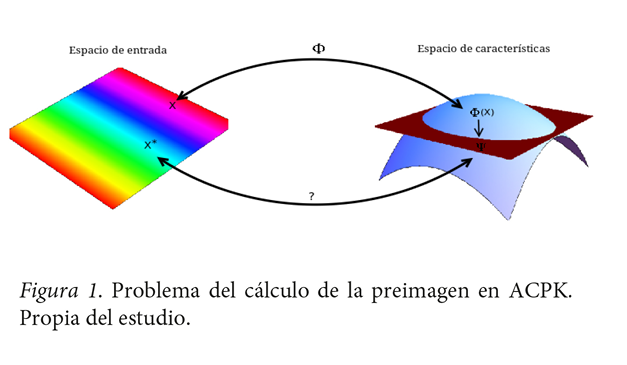
es l ‒ ésima entrada del i ‒ ésimo vector propio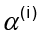
(Ver figura 1).
Experimento
Para ilustrar los métodos ACP, ACPP y ACPK, se trabajó en un experimento que ilustra la reconstrucción de los datos en el espacio de entrada respecto a un número de componentes principales necesarios que lo permitan y que sea menor al número de dimensiones original. La idea es ver como los datos pueden ser recuperados con un menor número de dimensiones que el espacio original.
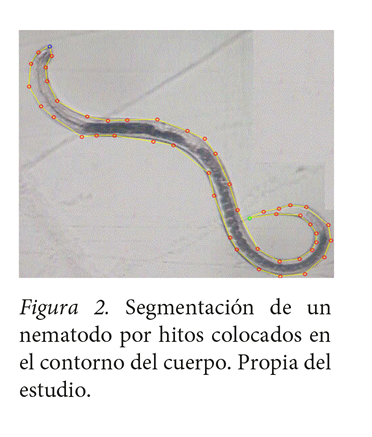
Base de datos. Para fines experimentales, se construyó una base de datos1 de 265 de formas de nematodos segmentados por hitos hi(x, y) colocados en su contorno y, obtenida a partir de imágenes digitales de microscopía en formato .png similares a la figura 2.
Para la construcción de la base de datos se desarrolló un software en el lenguaje c++ llamado HESEV2, en el que el usuario o usuaria coloca los hitos de forma secuencial en el contorno del nematodo. Entre cada par de hitos (líneas amarillas de la figura 2) se esboza una línea que en conjunto aproxima la silueta del nematodo segmentado. Por cada segmentación realizada se guarda un archivo que contiene un vector bidimensional de los hitos del nematodo. El proceso de segmentación inicial no contempla un número específico de hitos, con el fin de ser colocados de forma que se logre una descripción lo más objetiva de la silueta del nematodo.
Luego, se trabajó en un proceso de normalización sobre el número de hitos y su posicionamiento. Para esto, primeramente, se utilizó el método de interpolación paramétrico trazador cúbico natural (B-Splines) (Amini y Chen, 2001) para modelar la forma del nematodo a través de una curva. Es un proceso que traza una curva de manera continua de la forma C(S(t), S(t)) con t =1..., n, donde n representa el número de hitos con que se representó inicialmente y S la curva generada por el B-Spline. Posteriormente, se calculó la longitud de arco de C y se dividió en “m” partes de manera que los hitos resultaran colocados a una misma distancia.
Implementación de los MRD a la base de datos. La implementación de los algoritmos de los MRD en mención se realizó con el software Matlab, basado en el desarrollo teórico efectuado en la sección anterior.
Se eligieron 160 hitos por nematodo, se colocó el hito número 1 en la cabeza y el hito número 80 en la cola del nematodo para un total de 160 hitos por individuo, para un total de 265 nematodos segmentados.
Se ejecutó cada algoritmo con la base de datos en ejecuciones por separado para n componentes principales (n = 1, …, 265). En el caso del KPCA, se reconstruyeron las formas usando el método de cálculo de preimagen descrita en Arroyo y Alvarado (2014) y se eligió la función kernel radial gaussiana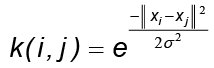 
con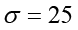 
.
Resultados experimentales y discusión final
A la base de datos de hitos de nematodos segmentados se le aplicaron los métodos ACP, ACPP y ACPK, con el fin de poder reconstruir las distintas formas de nematodos con un número menor de dimensiones al del espacio original.
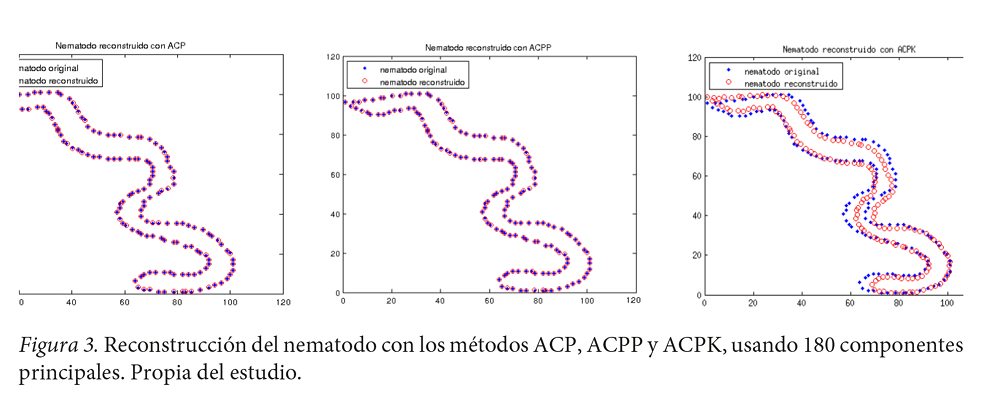
Los tres métodos ACP, ACPP y ACPK presentaron una reconstrucción aceptable forma con número de dimensiones cp (componentes principales) menor que el espacio original de datos. Sin embargo, el número de dimensiones es alto respecto al esperado, pues cp > 5 (Ver figura 3).
Asimismo, se calculó la raíz de error cuadrático medio (RECM). Los resultados arrojaron la siguiente relación entre la reconstrucción de los MRD descritos respecto a la cantidad de componentes principales para su reconstrucción: a mayor número de componentes principales mejor reconstrucción. Sin embargo, en el error indica la cantidad de píxeles por desplazamiento de los hitos del nematodo original respecto al reconstruido, lo cual hace ver que el error, en términos generales, es similar y sus diferencias no son significativas (Ver figura 4). Los métodos ACP y ACPP presentan un error muy similar, ACPK tiene un error mayor. Sin embargo, en todos los casos es alto respecto al número de componentes principales.
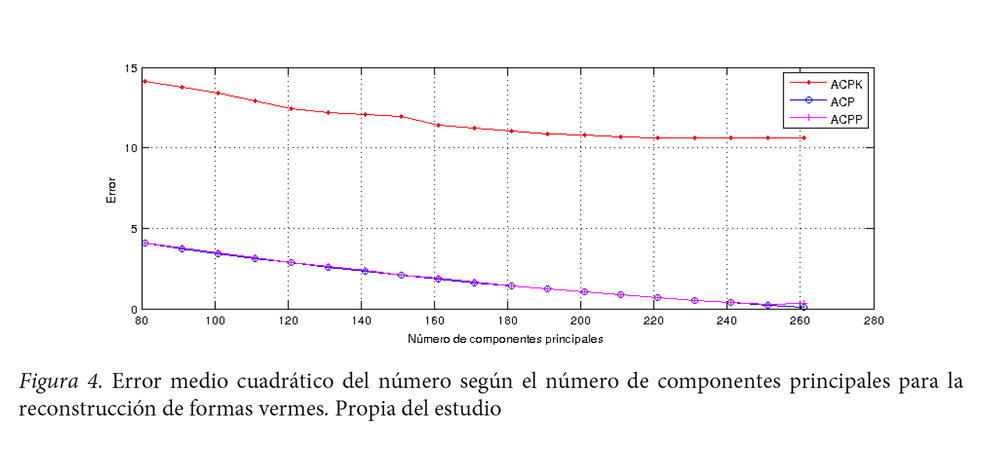
Un aspecto que influyó en la determinación de un número de componentes alto es la deformidad que presentan los nematodos. De hecho, la variabilidad vermiforme de los datos presentados es debido a las deformaciones por movimientos abruptos de los nematodos que hacen muy compleja una reducción de los datos. Aun así, fue posible disminuir a 180 componentes principales en el caso de ACKP, 80 componentes principales en el ACP y ACPP, para obtener reconstrucciones relativamente aceptables.
Una remarca importante es que se logra evidenciar un cálculo confiable de forma para el problema de la preimagen con el método de aproximación por mapas conformes utilizando la variante presentada por Arroyo y Alvarado (2014).
Finalmente, es importante mencionar que los tres casos presentados de MRD pueden verse como métodos alternativos, por su funcionalidad en cuanto a la reconstrucción de datos. Los tres logran ejecutarlo con una menor cantidad de dimensiones. Sin embargo, por el potencial que presenta el método ACPK para analizar los datos en el espacio de características y por los resultados del cálculo aproximado de su preimagen, este presenta una mejor fiabilidad para procesos de reconocimiento y extracción de patrones.
Referencias
Amini, A. A., Chen, Y., Elayyadi, M., & Radeva, P. (2001). Tag surface reconstruction and tracking of myocardial beads from SPAMM-MRI with parametric B-spline surfaces. Medical Imaging, IEEE Transactions on, 20(2), 94-103. Recuperado de doi http://dx.doi.org/10.1109/42.913176
Arroyo, J. y Alvarado, J. (2014). A new variant of Conformal Map Approach method for computing the preimage in Input Space. Recent Advances in Computer Engineering, Communications and Information Technology, 301-304 Recuperado de http://www.wseas.us/e-library/conferences/2014/Tenerife/INFORM/INFORM-00.pdf
Honeine, P. y Richard, C. (Marzo, 2011). Preimage Problem in Kernel-Based Machine Learning. IEEE Signal Processing Magazine, 28 (2), 77-88. Recuperado de http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5714388&isnumber=5714377
Lee, J. y Verleysen, M. (2007). Nonlinear Dimensionality Reduction. Springer. Science & Business. Estados Unidos. doi http://dx.doi.org/10.1007/978-0-387-39351-3
Shlens, J. (2005). A Tutorial on Principal Component Analysis. Systems Neurobiology Laboratory, Salk Institute for Biological Studies. Recuperado de http://arxiv.org/pdf/1404.1100v1.pdf
Scholkopf, B., Smola, A. y Müller, K. (1999). Kernel principal component analysis. Advances in Kernel Methods-Support vector Learning, 327-352. Recuperado de http://pca.narod.ru/scholkopf_kernel.pdf
Tipping, M. y Bishop, M. (1999). Probabilistic principal component analysis. Journal of the Royal Statistical Society. Series B, 61 (3), 611-622. Recuperado de doi http://dx.doi.org/10.1111/1467-9868.00196
Van der Maaten, L., Postma, E. y Van den Herik, H. (2009). Dimensionality Reduction: A Comparative Review. Technical Report TiCC TR. Recuperado de http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.125.6716&rep=rep1&type=pdf
